不同曲率空腹式连续刚构桥静动力分析
李高超,王春香
(1 长安大学公路学院,陕西 西安710064; 2 山东碧海建筑规划设计有限公司,山东 日照276500)
不同曲率空腹式连续刚构桥静动力分析
李高超1,王春香2
(1 长安大学公路学院,陕西 西安710064; 2 山东碧海建筑规划设计有限公司,山东 日照276500)
以一座空腹式连续刚构桥为工程背景,通过改变其主梁的曲率半径,分析了对以下几个方面的影响:恒载作用下结构的内力变化,地震动的最不利输入方向,结构的地震响应。计算结果表明:当曲率半径小于600 m时,恒载作用下各墩底的扭矩随曲率半径的增加而减小;而两中墩的弯矩随曲率半径的增大而减小,两边墩的弯矩亦是减小;超过600 m时,变化不大。不同地震波输入角度下,桥墩墩顶处的顺桥向和横桥向位移的最不利响应值不同时出现。不同曲率半径的桥梁结构在墩底处的弯矩和剪力变化趋势一致。随着曲率半径的不断增大,墩顶处顺桥向位移是不断增大的,墩底的顺桥向剪力和弯矩也是逐渐增大。
空腹式;刚构桥;曲率;静动力分析
对于大跨径桥梁而言,悬索桥、斜拉桥、拱桥和高墩连续刚构桥作为优先选择的方案,当跨径处于100~300 m范围内时,连续刚构桥的优势就体现出来了。连续刚构桥具有较大的刚度,跨越能力大,施工工艺成熟,尤其是高墩大跨连续刚构桥,往往被设计者广泛采用[1-2]。为了满足更多地区的需要,连续刚构桥的跨越能力将会进一步增大,但连续刚构桥存在经常出现裂缝和跨中下挠的问题[3-4]。上部结构轻型化是解决连续刚构桥现存问题的一种好办法。可以采取多种手段实现此目标,例如采用轻型混凝土结构、将实腹段负弯矩区挖空等方法。
空腹式连续刚构桥,它是在结构上对普通连续刚构桥的创新,其主要构思是将位于主梁根部位置处的腹板挖空,形成下弦下缘与实腹梁段连续曲线变化相对应的主梁空腹区。空腹式刚构桥在结构上 V 形斜腿与桥梁主墩、主梁相互连接组成三角区域,V 形斜腿起到了承受压力的功能,在材料上充分利用了混凝土承压能力高的优点,同时V 形斜腿还能显著的减小桥梁的相对跨径,使结构在受力方面更合理,从而其跨越能力也得到了很大的提高。宗昕等[5]以北盘江特大桥为工程实例,通过方案比选,确定了空腹式连续刚构这种新桥型,并对其进行了结构分析。该桥型不仅跨越能力较大,而且其关键截面受力合理。应松等[6]针对空腹式连续刚构桥无法使用支架进行施工的特点,提出了4种施工的方法,并对其在多方面进行了对比分析。宋恒扬等[7]以某空腹式连续刚构桥为背景,利用正交实验的方法,对其参数进行了对比分析。杨书杨[8]以伦洲大桥空腹式连续刚构桥为工程背景进行了相关的研究。
本文以某大跨空腹式连续刚构桥为工程背景,利用有限元程序MIDAS/CIVIL,分析了曲率半径的变化对结构静动力响应的影响,考虑了如下几个方面:恒载作用下结构的内力分布,地震动的最不利输入方向,结构的地震响应。本文的研究目的在于,通过分析得出相关结论,为今后同类桥梁的设计提供有益的参考,而不仅仅是就某一个特定的场地条件进行分析。
1 工程概况
本文以某座预应力混凝土空腹式(斜腿)连续刚构桥为工程背景进行分析。该桥主桥跨径布置为:(82.5+220+290+220+82.5)m。其中,主梁在实腹段采用变截面直腹板箱梁,在空心段上弦杆采用等截面直腹板箱梁,下弦杆采用等截面箱梁。桥墩采用空心双薄壁结构。利用有限元程序MIDAS/CIVIL进行建模,全桥全部采用空间梁单元进行模拟,梁和墩顶之间采用主从约束,未考虑桩基的影响,在承台底进行固结处理。全桥示意图及有限元模型如图1、图2所示,桥墩的编号也在图中进行了标注。

图1 总体布置图
2 分析工况
曲率半径是影响结构静动力响应的一个重要因素,因此本文分析了以下的工况,通过试算,发现对于恒载的内力变化规律来说,曲率半径为600 m时的影响近似处于1个驻值点上,因此从分析的角度选取了600 m附近的一些值进行讨论。同时为了简化分析,动力方面也考虑了这些工况。分析工况如表1所示。

图2 有限元模型总体布置图

曲率半径/m3004005006007001500∞静力分析√√√√√动力特性分析√√√√√√抗震分析√√√√√√
3 分析结果
3.1静力分析结果
为了更好地研究该参数在恒载作用下对空腹式刚构桥内力的影响,本节选取了曲率半径R分别为300 m、400 m、500 m、600 m、700 m的5种桥梁结构形式,在恒载作用下,由于弯扭耦合的影响,选取了墩底的扭矩和弯矩作为指标进行分析(抗震中主要关注墩的响应,此处为了统一,静力分析时也只关注墩的响应),结果如图3、图4所示。
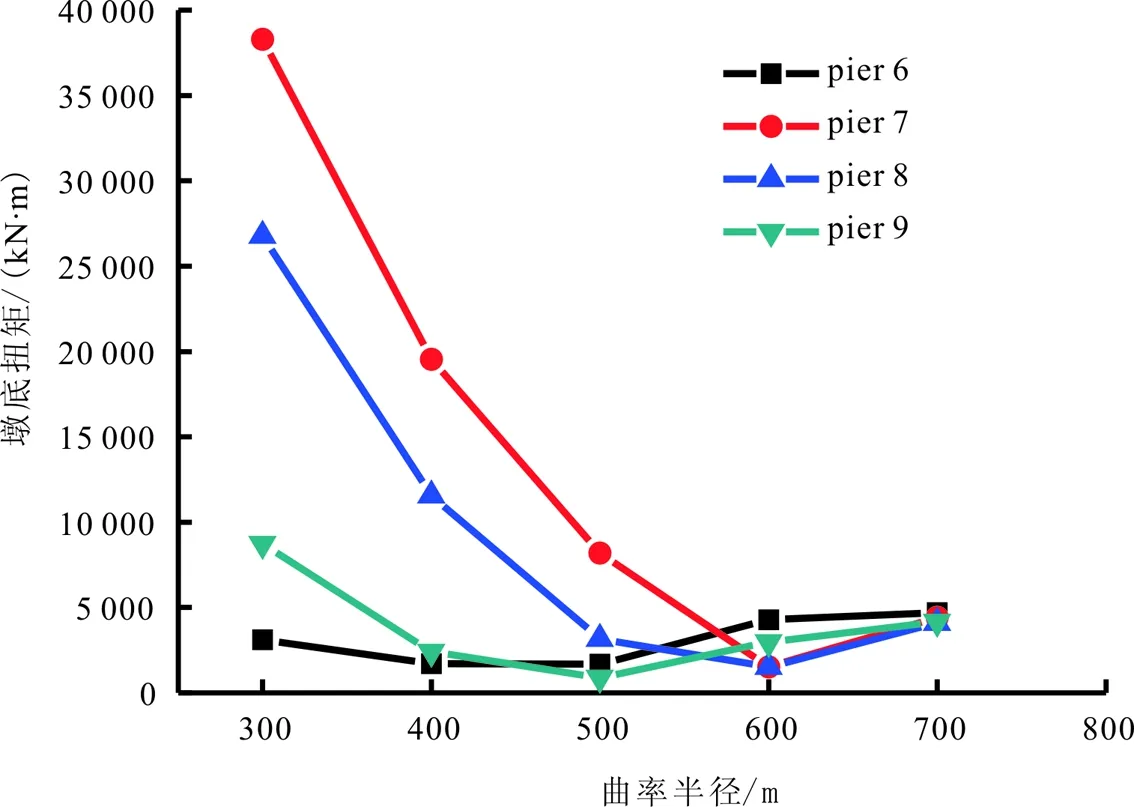
图3 不同曲率半径的墩底扭矩

图4 不同曲率半径的墩底弯矩
由图3可以看出,当曲率半径小于600 m时,恒载作用下各墩底的扭矩随曲率半径的增加而减小。并且当曲率半径较小时,中墩扭矩的数值明显大于边墩,即中墩扭矩对较小曲率半径的敏感程度比边墩显著。然而,随着曲率半径的继续增大(当曲率半径大于600 m时),各桥墩的扭矩虽然慢慢增大,但各墩的扭矩受曲率半径的影响甚微。由图4可以看出,在恒载作用下,两中墩的弯矩随曲率半径的增大而减小,而两边墩的弯矩却是先减小后增大,并且,中墩弯矩的数值明显大于边墩。
3.2动力分析结果
3.2.1不同曲率半径的动力特性
对于曲线梁桥来说,无论是上部结构的刚度还是质量在全桥的分配,都有可能会因为曲率半径的改变而发生变化。在其它条件与原桥均相同的情况下,改变曲率半径这一参数建立模型,比较曲率半径R分别为300 m、400 m、500 m、600 m、700 m、∞等6种桥梁结构的动力特性,前10阶在不同曲率半径时结构的自振特性如表2所示。

表2 不同曲率半径时结构的自振特性
当曲率半径增大时,结构的前3阶模态的周期逐渐增大,其他各阶模态的周期与之相反。其中,曲率半径对主梁一阶正对称横向弯曲振型所对应周期影响较大,对其他各阶影响不大。在曲率半径增大时,各相邻桥墩之间的相对距离变大,桥墩减小了对主梁跨中质量的制约,因此使周期增大。而在高阶振型中,桥墩的变形不同步,使得桥墩间的相对间距减小,从而使自振周期受曲率半径的影响程度变小。
曲率半径的不同,导致了弯扭耦合效应的分配比重不同,因此结构各阶周期是变化的。但是曲率半径对这种分配的效应比较小,各同阶周期间变化较小,故而振型出现的顺序一致。
随着曲率半径的变大,计算结果越接近于R=∞;且在6阶模态主梁发生竖弯时各半径的周期与半径为R=∞的周期最接近。因此,从计算冲击系数方面来说,当梁桥的曲率半径比较大时,为方便起见,可用直线梁桥来进行模拟。
3.2.2不同曲率半径的最不利地震动输入方向确定
由表2可以看出,对于类似本桥这种大跨径桥梁,其各个方向的一阶周期较大,属于长周期结构,因此本文选取了卓越周期较大的天然地震动进行分析。本文选取了MEXICO CITY波进行分析,其卓越频率位于0.5 Hz附近,峰值加速度为0.17 g。加速度时程和其对应的反应谱如图5所示。水平面内作用于结构的地震动一般可分解为两个相互垂直的方向[9-11],然而因为地震作用有强烈的随机性和不确定性,并且非常复杂,因此在抗震设计计算时,如何确定最不利输入方向是很困难的。就直线桥而言,由于纵桥向和横桥向是相互垂直的,故可把这两个方向作为其输入方向。但是对曲线梁桥而言,由于纵桥向是曲线的,其纵桥向的径向也是在不断改变的,所以就不能像直线桥一样单纯地把纵桥向和横桥向作为输入方向。并且,曲线梁桥的轴线并不是直线,有可能会在结构中出现弯扭耦合的现象,其纵桥向和横桥向就更加不明确。所以,曲线梁桥要尽可能多的输入任意方向进行计算分析,以确定最不利的地震输入方向。因此本文按20度的间隔进行不同方向的输入。不同方向的地震作用结果如图6~图9所示,由于桥梁近似对称,为节省篇幅,只给出了7号墩的结果。

(a)时程

(b)反应谱
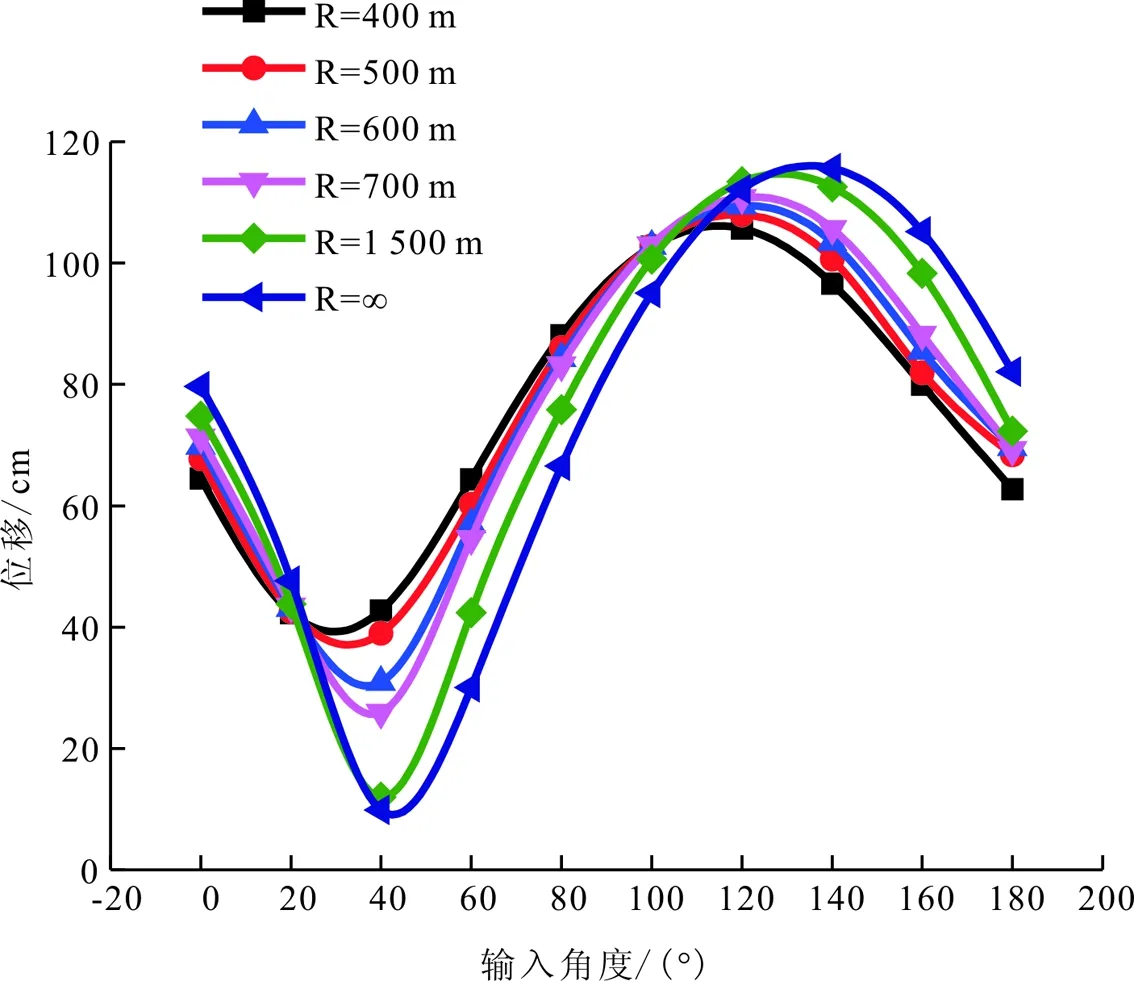
图6 墩顶处顺桥向位移
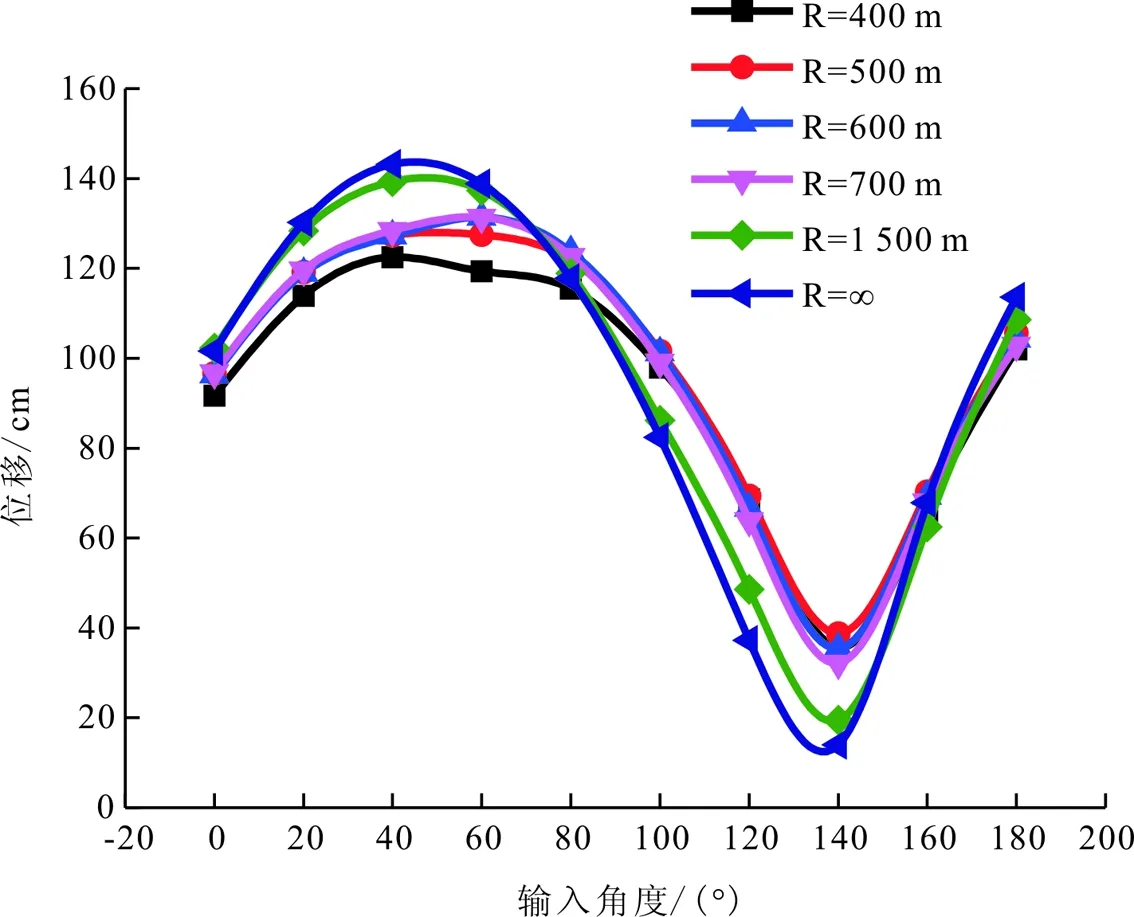
图7 墩顶处横桥向位移
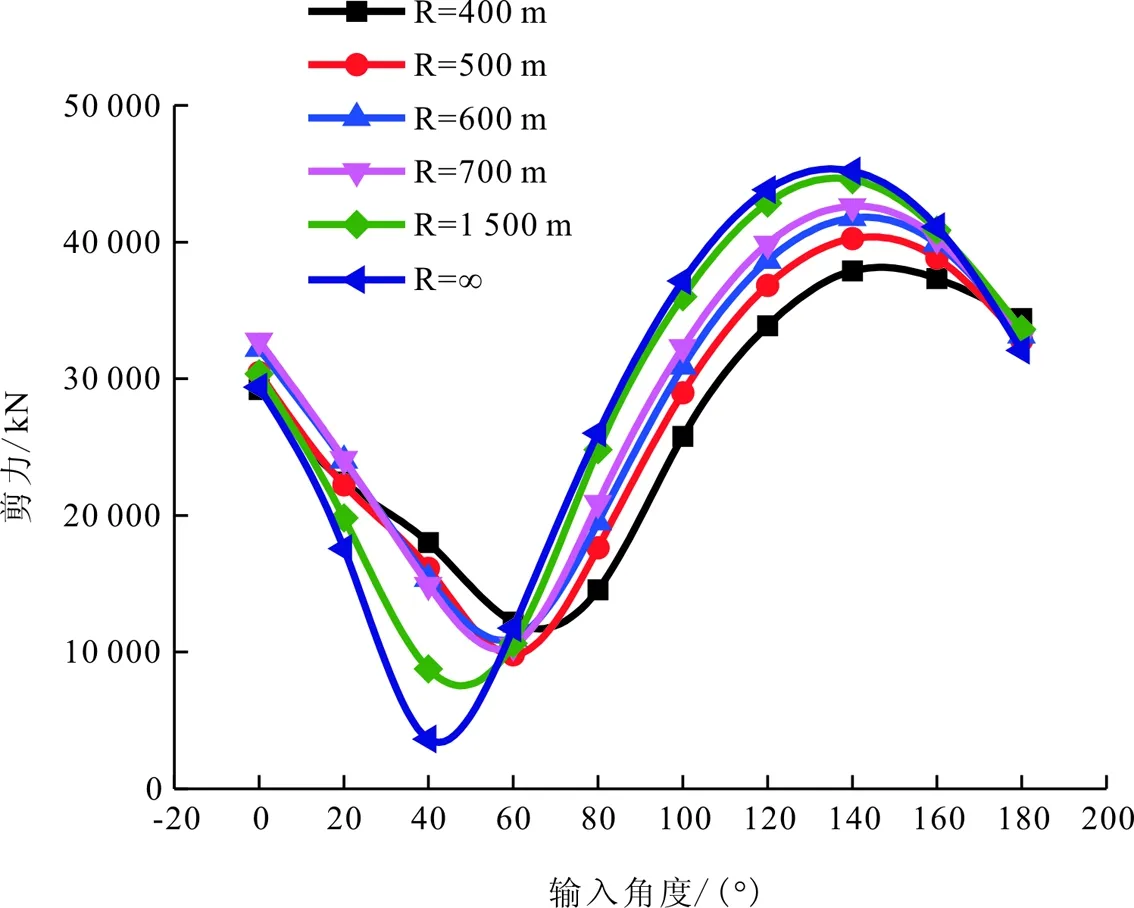
图8 墩底处剪力

图9 墩底处弯矩
由图6可以看出,不同曲率半径下,顺桥向位移随着地震波输入角度的改变而改变,但变化趋势基本相同。在输入角度为40°左右时,地震波作用下桥墩墩顶顺桥向位移最小,大约在140°左右时位移最大。由图7可以看出,桥墩墩顶处的横桥向位移,也是随着地震波输入角度的改变而改变,但其变化趋势,与顺桥向变化趋势相反。在输入角度为40°左右时,地震波作用下桥墩墩顶顺桥向位移最大,大约在140°左右时位移最小。
由图8~图9可以看出,在不同地震波输入角度0°~180°作用下,各曲率半径模型在桥墩墩底处的剪力变化趋势一致。与剪力变化相似,在不同地震波输入角度作用下,各曲率半径模型在桥墩墩底处的弯矩变化趋势一致,产生最不利弯矩响应的地震波输入角度也不同,但比较接近。
3.2.3不同曲率半径的地震响应
根据上节分析,选取卓越频率约为0.5 Hz的地震波,研究不同曲率的结构在地震波输入角度为140°时,桥墩墩顶位移、墩底的剪力和弯矩,其中墩顶的位移为斜腿与主梁相交的两处。

图10 曲率对墩顶处顺桥向位移的影响

图11 曲率对墩底剪力的影响

图12 曲率对墩底弯矩的影响
由图10可以看出,随着曲率半径的不断增大,墩顶处顺桥向位移也是不断增大的。计算的墩顶位移处分别为斜腿与主梁相交的两处,这两个桥墩的位移基本成对称的形式,但是两个桥墩的位移值却又不完全相同,说明水平地震波对曲线桥梁不同位置地震响应的影响不同。
由图11~图12可以看出,墩底的顺桥向剪力和弯矩随曲率半径的增大而增大,8#墩墩底处的剪力要比7#墩墩底处大得多,而顺桥向弯矩则与之相反。
4 结论
针对大跨径空腹式连续刚构桥,本文研究了其参数的变化对地震相应的影响,得出的结论为:
(1)当曲率半径小于600 m时,恒载作用下各墩底的扭矩随曲率半径的增加而减小,而对于弯矩,两中墩的弯矩随曲率半径的增大而减小,而两边墩的弯矩亦随之减小;当曲率半径大于或等于600 m时,各墩扭矩增大不明显,且各墩扭矩数值相当。对于弯矩,中墩弯矩递减而边墩弯矩增大不明显,但中墩弯矩远大于边墩。
(2)桥墩墩顶处的顺桥向和横桥向位移的最不利响应值,并不是在地震波相同的输入角度作用下产生。顺桥向和横桥向位移各自的变化趋势大致相同,其出现的地震波最不利响应大约都出现在相同的角度,但具体值却又有所差异。
(3)在不同地震波输入角度0°~180°作用下,各曲率半径模型在桥墩墩底处的弯矩剪力变化趋势一致。最大值虽不同,但比较接近。
(4)随着曲率半径的不断增大,墩顶处顺桥向位移也是不断增大的。墩底的顺桥向剪力和弯矩随曲率半径的增大而增大。
[1]范立础. 桥梁工程 (上册) [M]. 北京:人民交通出版社,2001.
[2]马保林. 高墩大跨径曲线连续刚构桥变形控制研究[D].西安:长安大学,2006.
[3]孙剑川. 预应力混凝土连续刚构桥下挠问题研究[D]. 成都:西南交通大学,2010.
[4]周军生,楼庄鸿. 大跨径预应力混凝土连续刚构桥的现状和发展趋势[J]. 中国公路学报,2000,13(1):31-37.
[5]宗昕,彭元诚,吴游宇,等. 北盘江特大桥结构设计[J].公路,2010(8):22-25.
[6]郑则群,房贞政,陈红媛. 空腹式刚架拱桥有机玻璃模型试验[J]. 工业建筑,2008,38(6):43-47.
[7]宋恒扬,胡俊,彭元诚. 空腹式连续刚构桥设计参数的正交试验研究[J]. 世界桥梁, 2015,43(1):55-58.
[8]杨书杨. 新型空腹式刚构桥与普通刚构桥的对比分析[D].武汉:华中科技大学,2013.
[9]中华人民共和国住房和城乡建设部.CJJ 166—2011城市桥梁抗震设计规范[S].北京:中国建筑工业出版社,2011.
[10]叶爱君,管仲国. 桥梁抗震[M].北京:人民交通出版社,2011.
[11]中华人民共和国交通运输部. 公路桥梁抗震设计细则:JTG/T B02-01—2008[S].北京:人民交通出版社,2008.
Static and dynamic analysis of open-web continuous rigid frame bridges with different curvatures
LI Gao-chao1,WANG Chun-xiang2
(1.SchoolofHighway,Chang′anUniversity,Xi′an710064,China;2.ShandongBihaiArchitecturalDesignLtd.Co.,Ri′zhao276500,China)
Taking an open-web continuous rigid frame bridge as example,this paper took the following cases into consideration which were that internal force’s laws under dead load,the most unfavorable input direction of earthquake wave and response under earthquake load with different curvatures.Through analyses,some conclusions could be obtained.When the curvature radius is less than 600 m,the bottom torsion of every pier and the middle pier bending moment reduce with the growing radius under dead load while the side pier bending moment also gains and the response changes little when the radius exceeds 600 m.In different angles,the most unfavorable responses of top pier longitudinal and transverse displacements don’t happen in the same angle.The tendency of bottom pier shear and bending moment is similar.With the increasing radius,the top pier longitudinal displacement grows and so are the longitudinal shear and bending moment.
open-web;rigid frame bridges;curvature;static and dynamic analyses
2015-12-24
李高超(1990—),男,陕西西安人,硕士研究生。
1674-7046(2016)02-0041-07
10.14140/j.cnki.hncjxb.2016.02.008
U448.23
A

