高层不规则钢结构体系的抗震性能研究

张经纬，雷庆关，华　奎，章雨健

(安徽建筑大学，安徽 合肥 230601)



高层不规则钢结构体系的抗震性能研究

张经纬，雷庆关，华奎，章雨健

(安徽建筑大学，安徽 合肥 230601)

应用软件SAP2000针对不规则钢结构分别建立加支撑和未加支撑2种结构模型，对2个结构进行弹性模态分析、结构的反应谱分析以及结构的线性时程分析，通过上述分析得出结构的质量参与系数、前12阶自振周期、基本动力特性，经过数据比较两个模型的层间位移，分析计算得出层间位移角，根据所得数据判断并评估结构的抗震性能。表明加结构支撑的结构布置能提供一定的抗扭刚度，使结构保持良好的变形，从而有效提高结构抗震减震性能。

不规则钢结构；弹性时程分析；模态分析；抗震性能研究

我国的地理位置处于一个地震多发的区域，随着我国城镇化进程的推进以及人口分布越来越集中，任何一次的强震都会给人们带来十分严重的损害。尤其是对于不规则建筑，结构本身的抗震水平和有效地加固防震措施尤为重要。所以，根据实际情况针对高层不规则钢结构以及与之相关的抗震理论研究是十分有意义的。钢结构本身的可靠性大，给所设计的房屋整体结构提供了可靠的整体性能以及足够的抗震安全性能[1]；另一方面钢结构表现出了所独有的轻质高强的优良特点，足以使结构本身所受的地震作用影响有效降低，使房屋结构在地震作用下少受影响。

本文根据结构的不规则布置情况，采用SAP2000软件进行合理分析，通过数据进行结构在有、无支撑时结构的层间位移和位移角的分析对比，得出两类结构的地震响应，研究评估结构的抗震性能。

1　工程简介以及工程超限认定

1.1工程简介

此结构体系为不规则钢框架结构，层数为10层。型钢梁、全固接栓焊框架、箱型柱，根据结构体系特性设了合理的支撑，使得满足了相应的变形要求。结构优点就是施工简单，节约工程用钢及其他施工耗材。设计的结构层高3.3 m，柱间距均为6 m，柱截面为450mm×450 mm；梁的截面为300mm×600 mm。根据规范规定，本文结构符合相关要求。结构抗震设防烈度按照要求为8度；结构活载以及结构静荷载分别为2.0 kN/m2、5.0 kN/m2；结构梁上线荷载为：10 kN/m；此结构为II类结构场地类型。

1.2工程结构超限认定情况

根据《建筑抗震设计规范》第3.4.3条关于平面不规则的主要类型的规定，有下列三类主要类型[2]：

第一种是凹凸不规则：即投影方向总尺寸的三分之一应该在理论上小于平面凹进的计算数值；

第二种是扭转不规则：就是在要求的水平力作用下，结构体系的各个楼层之间的两端弹性水平位移平均值乘以1.2所得数值理论上小于其对应的该楼层的最大弹性水平位移的数值，其结构体系的各个楼层之间的层间位移的要求亦是如此；

第三种则是楼板局部不连续：就是指楼板的平面刚度产生急剧变化亦或者是楼板的平面尺寸产生急剧变化，比如，某层楼板宽度的一半，其数值大于或者远远大于有效楼板宽度，或该层计算得出的楼面面积的三分之一数值小于或远远小于该层楼计算得出的开洞面积总和的数值，亦或者本结构的楼层设计之中存在有超出一般理论的楼层错层情况而造成的楼板局部不连续发生。

根据《建筑抗震设计规范》：建筑不规则结构主要可从定义上分为2种不规则结构体系即平面方向、竖直方向的不规则结构布局，不论哪一种情况的不规则，只要存在于结构之中，则在实际情况下都应该加强对不规则结构的建筑实施相关的理论论证。

根据计算以及SAP2000建模结果易得出此工程为平面上的不规则结构。图1是未加支撑结构体系；图2是在结构第一层加上X型支撑结构体系(简称加支撑结构)。

图1　未加支撑结构体系

图2　加支撑结构体系

2　结构的抗震理论及相关分析

质点i上的惯性力为：

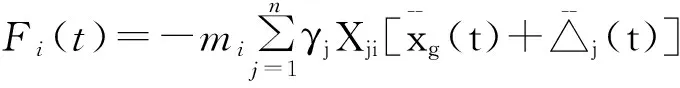
(1)

令

在第j振型作用影响下在i质点上所承受的地震作用绝对最大值为

Fji=αjγjXjiGi

(2)

式中：Fji为第j振型第i质点水平地震作用标准值；αj为第j振型下的自振周期的影响系数；γj为第j振型下的参与系数；Xji为第j振型作用下的第i质点的相对水平位移；Gi为集中于i质点的重力荷载代表值，G=mig。

振型分解理论是将每一个地震作用力对应一个振型，再通过一定的作用力组合方法，可以达到地震影响的最终响应值。为了可以充分考虑由于振型阻尼这个重要因素所引起事件之间的关联性，即静态耦合效应等成分，故以随机振动理论为根本理论依据而得出的完全二次振型组合方法在理论上是比较合理的振型组合方法。

此外为了得出该质点构件的内力和构件变形，计算在地震作用下某个质点随着时间变化的质点相关位移、质点速度以及该质点加速度，就需要采用时程分析的方法，其运动方程为：

(3)

3　结构计算分析

3.1模态分析

模态分析实质上是一种坐标变换，通过对结构或部件的试验数据处理和分析，测得较为精确的固有频率、模态振型、模态阻尼等。依据SAP2000软件针对该工程实例在仿真地震作用情况下进行工程的整体结构体系分析。设计要求此结构计算模型假定之中楼板采用刚性楼板，其结构之中使用的梁、柱均采用的是空间杆单元。结构的模态分析是线性结构体系在地震分析中重要的方法[3]。因为模态分析不仅仅能够为结构提供足够的动力分析的基础，而且还能够为静力分析提供充分的相关结构性能[3]。此结构采用SAP2000对结构进行相关分析。依照SAP2000软件的分析所得本结构前12阶的结构体系自振周期和结构体系质量参与系数如表1所示。

此结构的平扭属性是严格按照质量参与系数状态来判断得出的参数结果进行评判的。在表1中，第一周期里的UX=0.717、UY=0.001，充分且客观的表明了在这一周期里，结构的平动振型是属于X方向的。根据UX方向平动的质量相关理论里所说的大多数都是绕X轴旋转的，从而验证了RY=0.811理论上是与UX相对应的。鉴于结构在平面X和平面Y上有约束产生，并且RX=0.004，RZ=0.020，在数值上，就充分客观的表明RZ是另一个质量参与系数。根据数据，有UX远远大于RZ和RY，这一理论计算结果充分说明此振型的平动振型主要是X方向的。同理，在第2振型之中，UX=0.001、UY=737，与之相应的RY=0.006、RX=0.799，RZ则显然小于UY。计算结果充分说明这一振型主要为Y方向。在第3振型之中，其UX=0.019、UY=0.009，与此质量参与系数所对应的RX=0.091、RY=0.019、RZ=0.417，数据结果客观地显示了RZ>RX>RY，即说明第3振型为扭转振型。在该结构的布置之中从第一阶平动阵型的数值就能够充分说明该结构是以平动为主并且具有相当的抗扭刚度。

按照建筑抗震设计规范之中要求，分析所有的质量参与系数要求其中所涉及的水平质量参与系数必须严格达到90% 以上才符合技术理论要求，这类数据须由SUM(UX)和SUM(UY)实施数据累加，且只要最终求和所得的振型质量。从表1中可以看出SUM(UX)为98.1%，SUM(UY)为94.4%，其结果均是满足规范要求的。

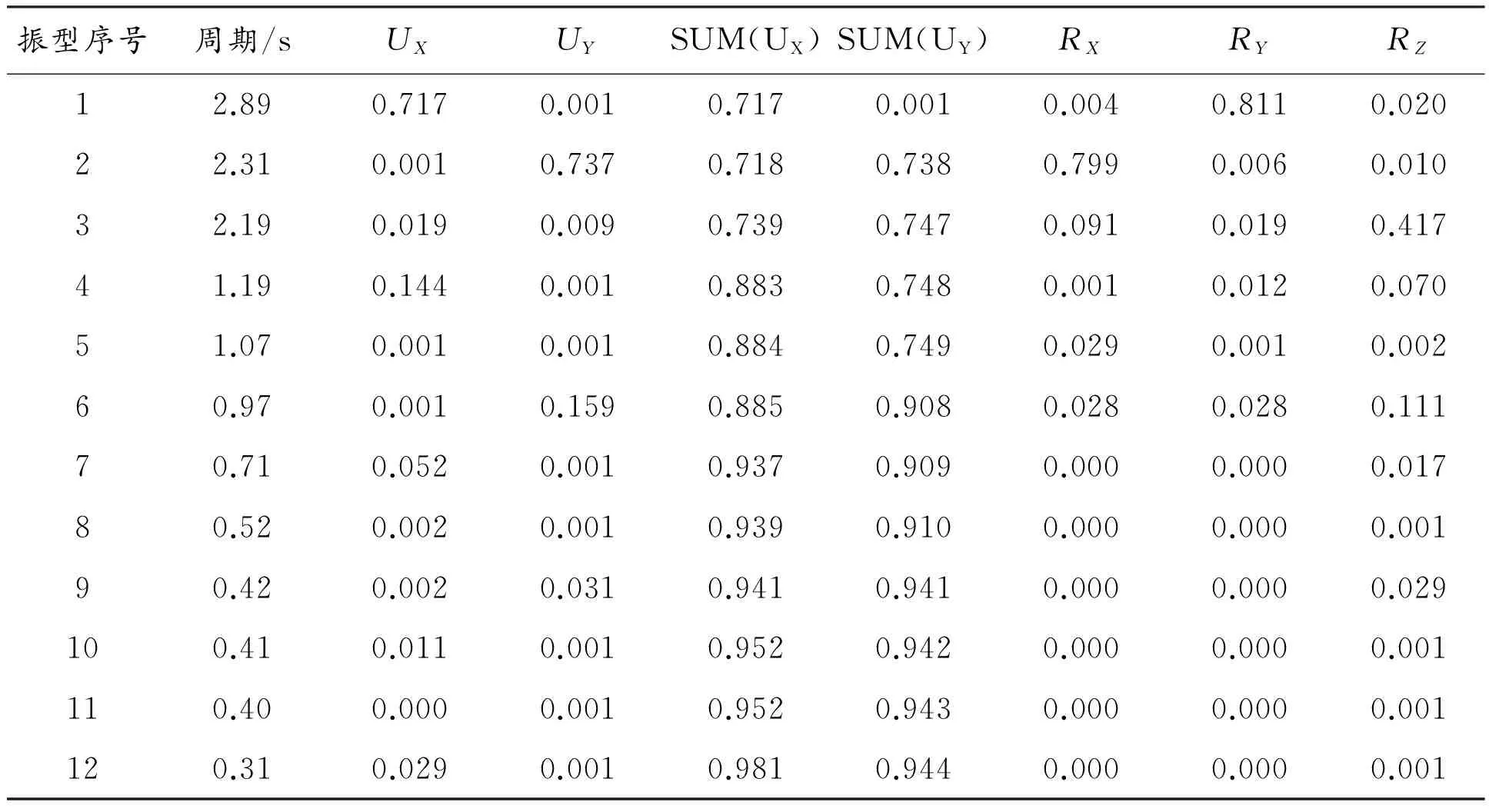
表1　未加支撑工程结构体系自振周期及其相应的质量参与系数

3.2反应谱分析

振型分解反应谱法是用来计算多自由度体系地震作用的一种方法。该法是利用单自由度体系的加速度设计反应谱和振型分解的原理，求解各阶振型对应的等效地震作用，然后按照一定的组合原则对各阶振型的地震作用效应进行组合，从而得到多自由度体系的地震作用效应。根据SAP2000对所设计模型进行反应谱计算所得数据如表2所示。

表2　未加支撑结构体系各个楼层的最大位移和与之对应的位移角

未加支撑结构依据反应谱分析法分析计算所得的4个相关位移包络图以及与之对应的位移图如图3～图6所示。

图3　纵向最大位移楼层结构体系包络图

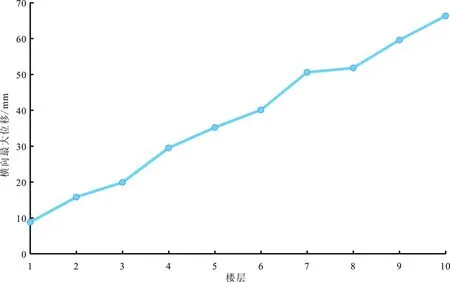
图4　横向最大位移楼层结构体系包络图

图5　纵向层间位移角结构体系包络图

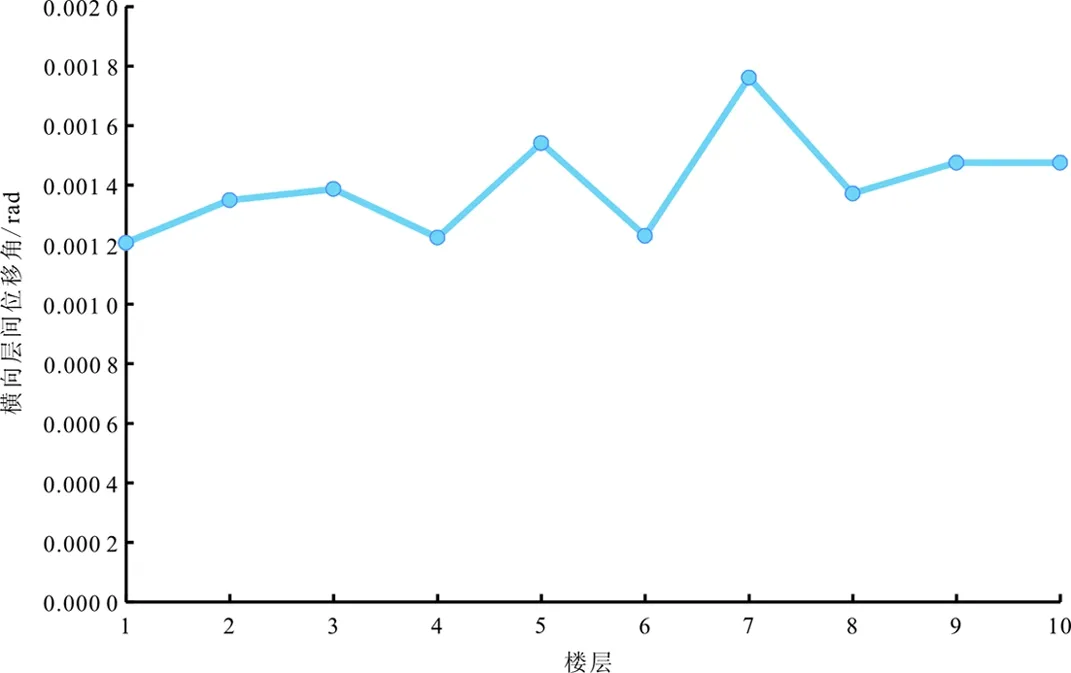
图6　横向层间位移角结构体系包络图

加支撑结构体系各个楼层的最大位移和与之对应的位移角如表3所示。加支撑结构依据反应谱分析法分析计算所得的4个相关位移包络图以及与之对应的位移图如图7～图10所示。

表3　加支撑结构体系各个楼层的最大位移和与之对应的位移角

图7　 纵向最大位移楼层结构体系包络图

图8　横向最大位移楼层结构体系包络图

图9　纵向层间位移角结构体系包络图

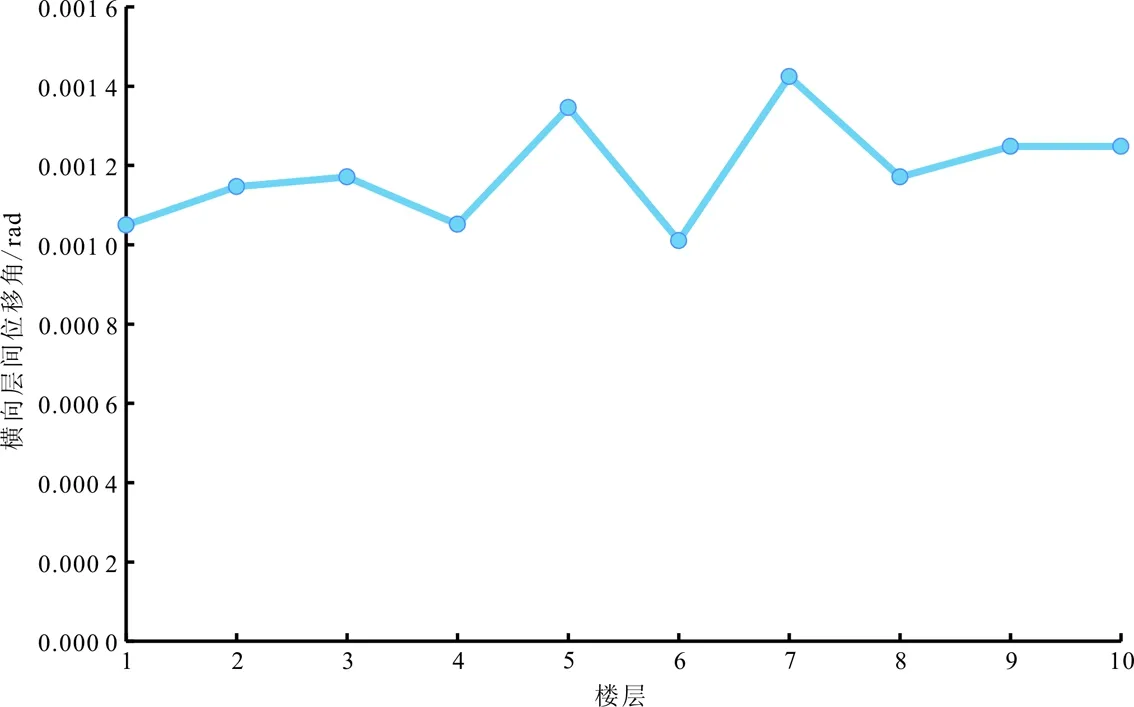
图10　横向层间位移角结构体系包络图

纵向位移和横向位移加上支撑后分别减少了15.2 mm和35 mm。在第7层，未加支撑前纵向最大层间位移角为1/391、横向最大层间位移角为1/568，加支撑之后显著减少到1/486和1/702，两数值均小于《建筑抗震设计规范》细则中的第5.5.1条规定务必满足弹性层间位移角低于规定限值即1/250[2]，支撑数量并非很多，对于建筑的影响却很大，数据显示结构是偏于安全的，能够达到大大减小体系变形和扭转效应的作用。

3.3弹性结构时程分析

根据《抗规》中的第5.1.2条规定[2]：“在地震情况下，针对各类不规则的建筑工程设计情况，除应用基本的计算程序之外还应该同时用时程分析法增加必要的相关验证的计算。”弹性结构时程分析由于能充分的反映出结构在计算中每一时刻的位移、每一时刻的速度和每一时刻的加速度，相对比于反应谱法却只能得出这个结构体系在多遇地震反应下的最大值，其优点是弹性结构时程分析理论上更为接近结构真实动力响应[5]。根据实际情况人们对于地震波选取有三种选择方案[6-7]：(1)选取相应的有代表性的地震记录；(2)选取相应的实际的地震波记录；(3)根据实际情况人工合成地震波。本文根据实际情况，主要取用的是Taft波、EL波和人工合成波Tangshan波。结构未加支撑与加支撑后各个结构层之间的最大位移和各个层间位移角如表4、表5所示，相应包络图如图11～图13所示。

表4　未加支撑时结构各个楼层最大位移与所对应楼层的层间位移角

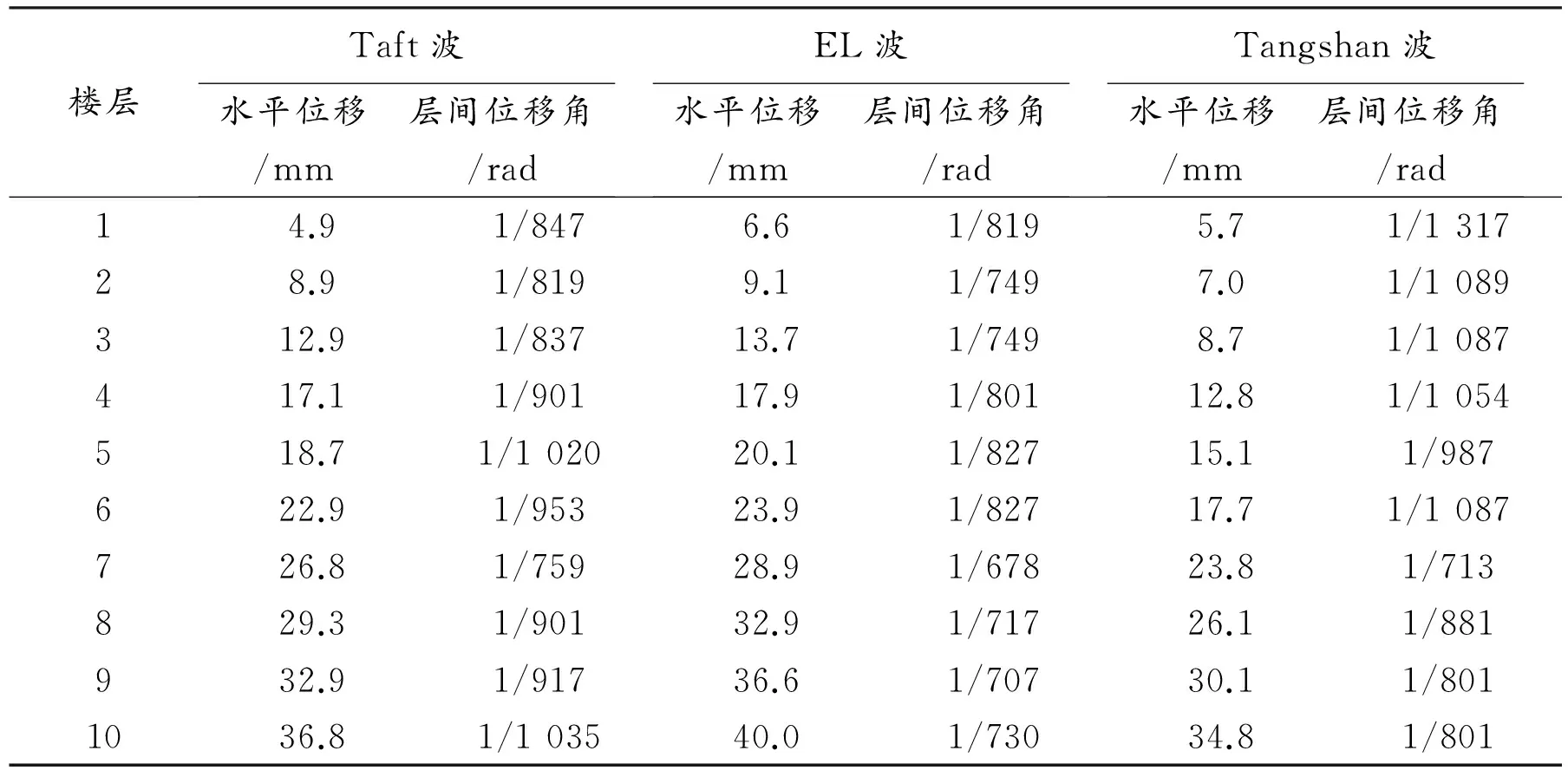
表5　 加支撑时结构各个楼层最大位移与所对应楼层的层间位移角

图11　Taft波时程分析下两模型位移包络图

图12　EL波时程分析下两模型水平位移包络图

图13　Tangshan波时程分析下两模型水平位移包络图

上述图表显示了结构支撑对于结构在时程分析下的影响程度，Taft波之中在未加支撑时横向最大位移为41.4 mm，加上支撑之后显著减小，降至36.8 mm；EL波之中结构在未加支撑时横向最大位移为48.8 mm，加上支撑之后降至40 mm，结构有无支撑对于此波影响最大；Tangshan波之中结构在未加支撑时横向最大位移为39.1 mm，加上支撑之后降至34.8 mm。显然有支撑时结构刚度均有所增加，达到了增加刚度以增加抗震性能的目的。

根据《抗规》5.1.2规定[2]：就是要求振型分解反应谱法计算所得数值的0.65倍，理论上应该大于每条时程曲线根据表格数据所得的底部结构剪力。所以计算的时程分析的计算位移是大于反应谱的计算位移即是合理的，同时可认定，结构弹性时程分析的合理性是优于反应谱法的。

4　小结

(1)结构的层间位移和位移角会随着结构层数增加而增大，且在反应谱分析下各楼层层间位移角均小于弹性层间位移角限值即1/250。

(2)为了充分说明该结构是具有相应的位移变形，能够保证结构可以提供相应的抗扭刚度，在结构的模态分析下通过前三阶振型验证，即结构的平动振型Y、X方向和结构的扭转振型。

(3)有结构支撑时位移显著降低，说明支撑给结构提供了相应的刚度。EL波位移数据减少的量是大于其它两个波位移减少量，说明有支撑时EL波下减震抗震效果最明显。

(4)所计算的时程分析的计算位移大于反应谱的计算位移是合理的，同时可认定，结构在弹性阶段弹性时程分析的合理性是优于反应谱法的。

[1]高层建筑混凝土结构技术规程：JGJ 3-2010[S].北京：中国建筑工业出版社，2011.

[2]建筑抗震设计规范：GB 50011-2010[S].北京：中国建筑工业出版社，2011.

[3]雷庆关,陈东.SAP2000在“结构动力学”中的应用探讨[J].安徽建筑工业学院学报(自然科学版),2012,20(3)：56-58.

[4]陆国威.新型轻钢龙骨结构多层住宅技术经济研究[D].武汉：武汉理工大学，2005.

[5]柳炳康，沈小璞.工程结构抗震设计[M].武汉：武汉理工大学出版社，2005.

[6]易方民，高小旺，苏经宇.建筑抗震设计规范理解与应用[M].2版.北京：中国建筑工业出版社，2011.

[7]李爱群,高振世,张志强.工程结构抗震与防灾[M].南京:东南大学出版社,2012.

[8]雷庆关，邱维.交错桁架结构的地震响应分析[J].安徽建筑工业学院学报(自然科学版)，2013,21(1)：6-8.

[9]Taranath B S. Structure analysis and design of tall Building[M]. New York:Mc Graw-FE, 1988.

[10]朱镜清.结构抗震分析原理[M].北京：地震出版社,2002.

[11]窦立军.建筑结构抗震[M].北京：机械工业出版社,2006.

[12]ATC-40.Seismic Evaluation and Retrofit of Concrete Building,Redwood City,CABSL2000,Building Standard Law[S]，2000.

[13]陈绍蕃.钢结构设计原理 [M].3版.北京：科学出版社，2005.

High-level seismic performance of irregular steel housing structure system

ZHANG Jing-wei,LEI Qing-guan,HUA Kui,ZHANG Yu-jian

(AnhuiJianzhuUniversity,Hefei230601,China)

Two kinds of structural models of structure with and without support were established by using SAP2000,and elastic modal analysis,linear response spectrum analysis as well as time history analysis of structure were performed.Mass participation factor of structure,the former 12th order vibration period,basic dynamic characteristics were obtained by the above analysis.Through the data,compare interlayer displacement of the two models,calculate the angle of displacement,and determine and evaluate the seismic performance architecture according to the data obtained.Results showed that structure with support can provide torsional stiffness and keep the structure in good deformation,thus effectively improving seismic cushioning properties.

irregular steel;elastic time history analysis;modal analysis;study on seismic performance

2016-01-26

安徽省高等学校自然科学研究重大项目(KJ2014ZD07)

张经纬(1991—)，男，安徽滁州人，硕士研究生。

1674-7046(2016)02-0016-08

10.14140/j.cnki.hncjxb.2016.02.004

TU973+.13

A