十形闭口截面压弯构件整体稳定性分析
赵滇生,郑舒蘅
(浙江工业大学建筑工程学院,浙江 杭州 310014)
十形闭口截面压弯构件整体稳定性分析
赵滇生,郑舒蘅
(浙江工业大学建筑工程学院,浙江 杭州 310014)
根据能量法推导十形闭口截面构件压弯临界屈曲方程,进而求解得到实用计算公式,再使用ANSYS有限元软件分析其在单向压弯下的屈曲性能。并分析材料非线性、几何非线性和残余应力等因素影响下长细比对该类截面钢柱整体稳定性的影响。
十形闭口截面;稳定性;非线性;长细比;ANSYS
现今多高层民用钢结构住宅中多使用箱型或H型钢柱,室内出现凸角,影响建筑美感和使用功能。钢结构异形柱能够完美地解决上述的问题[1]。本文将根据能量法推导任意闭口截面钢柱的微分方程,通过求解弯扭屈曲平衡方程得到实用计算公式。再通过有限元分析各类非线性情况下钢柱的稳定性能。
1 十形闭口截面压弯构件理论公式的推导
1.1十形闭口截面压弯构件屈曲荷载的推导
根据薄壁杆件理论和能量变分原理,由压弯构件屈曲时的总势能П的一阶变分δП=0,可以得到十形闭口截面压弯构件弯扭屈曲平衡微分方程:
(1)
式中:u、v分别为截面变形后的x、y方向位移;
φ为截面扭转角;
B为双力矩;
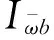
E1为换算弹性模量;
i0为对剪心的极回转半径;
A为截面面积。
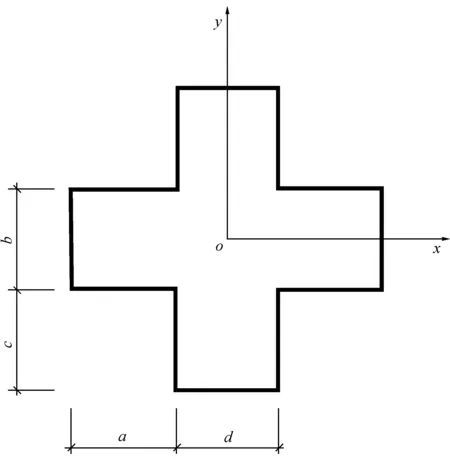
图1 十形闭口截面钢柱截面
忽略屈曲前变形的影响,将两端简支的边界条件代入式(1)可得十形闭口截面钢柱弯扭屈曲内力相关方程:
(2)
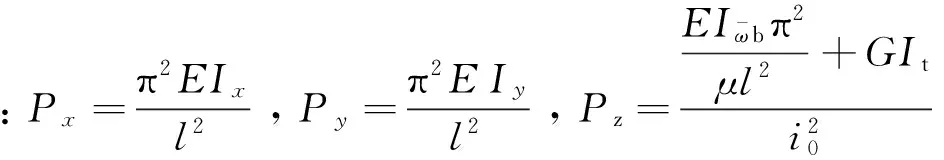
将 Mx=-P·ey,My=-P·ex代入式(2)中,化简后可得关于P的一元三次方程:
AP3+BP2+CP+D=0
(3)
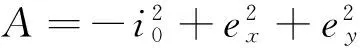
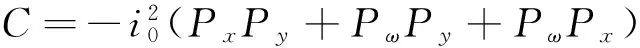

求解一元三次方程(3),可得三个根,其中最小实要即为构件屈曲的临界荷载Pcr。
1.2十形闭口截面压弯构件实用计算公式
设十形闭口截面构件为单向压弯,将式(3)进行适当地简化可以得到在工程中适用的线性公式[2]:
(4)
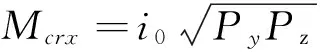
考虑二阶效应与初始缺陷的影响后,将式(4)转化为
(5)
式中:Pcr为构件无弯矩作用时的受压极限荷载;
Py为构件受压全截面屈服时的承载力,Py=Afy。
令Pcr/Py=φx,考虑部分截面塑性发展系数γx,式(5)可写成:
(6)
式中:Wx为弯矩作用平面内较大受压纤维的毛截面抵抗矩;φx为弯矩作用平面内轴心受压杆件的稳定系数;
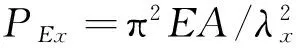
将Py=φyAfy与Mcrx=φbxWxfy代入式(4)中,并且考虑材料的分项系数后可得弯矩作用平面外的稳定验算公式:
(7)
式中:φy为弯矩作用平面外轴心压杆的稳定系数;φbx为均匀弯矩作用受弯构件的整体稳定系数。
2 十形闭口截面压弯构件整体弹塑性稳定性分析
2.1有限元弹性分析
采用通用有限元软件ANSYS,选取SHELL181壳单元分析。约束构件两端节点的水平位移,以及柱底截面失稳主轴两侧节点的纵向位移,以模拟两端铰接。构件两端截面施加与轴力和弯矩等效节点集中力。
根据图1所示,选取a=200mm,b=240mm,c=180mm,d=240mm,壁厚t=10mm的十形闭口截面,变化长细比,来分析压弯构件屈曲性能,屈曲特征值与理论推导值见表1。
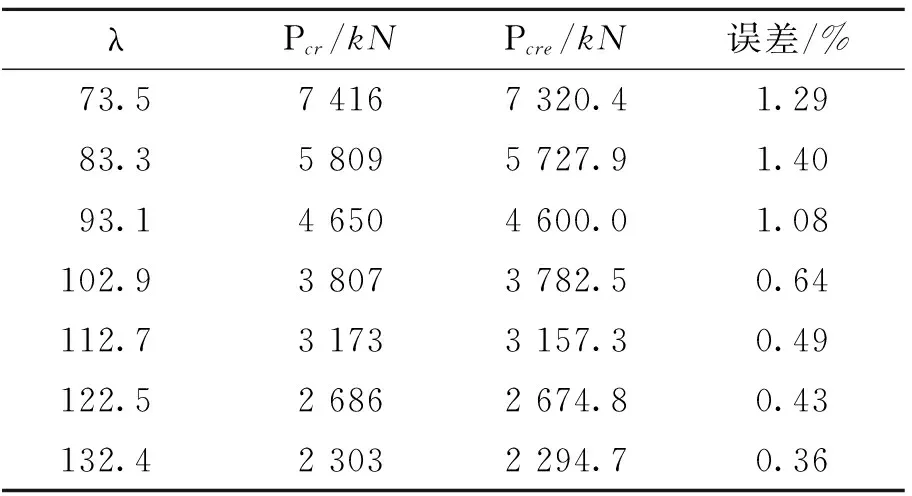
表1 十形截面柱特征屈曲分析
注:Pcr为理论推导值,Pcre为有限元分析特征值;误差=(Pcr-Pcre)/Pcr。
由表1 可见,特征屈曲值和理论值的误差均在1.5%以下,并且随着长细比增加误差减小。证明了理论推导值与模型均为正确。
2.2初始缺陷的影响分析
因实际工程钢构件的初始几何缺陷与力学缺陷会降低压弯构件的整体稳定性,有限元计算中考虑这些不利因素的影响。根据钢结构施工质量规范中允许的误差,取构件的初弯曲为长度的1/1 000。残余应力分布模式和峰值参考文献[3]选取。选取截面尺寸为a=150mm,b=200mm,c=150mm,d=200mm,t=10mm的GZ1。残余应力的分布模式与加载模型见图2。

图2 钢柱长、短边残余应力分布模式及加载模型
2.3构件长细比对稳定承载力的影响
针对GZ1截面的压弯构件,施加弯矩M/Mp为0~1。通过有限元分析,可以得到构件屈曲极限荷载值P。计算出不同长细比下P/Py,M/My的比值列于表2,两者的相关关系曲线见图3。

表2 不同长细比十形闭口截面钢柱有限元计算结果

图3 不同长细比弯矩-轴力相关关系曲线
由表2和图3可知:
1)当构件承受的弯矩较小时,其极限轴力随长细比的增加而降低,长细比大的构件更容易失稳;
2)弯矩较大时,构件长细比对极限轴力的影响不大。说明长细比主要会对十形闭口截面薄壁钢柱的轴压承载力产生影响,而对弯矩的影响不明显。
2.4实用公式的验证
对前文推导出的实用计算公式,不考虑弯矩不对称以及截面塑性发展系数的影响:
(8)
将表2中有限元计算出的P/Py代入式中便可反算出M/Mp的值。得到实用公式计算出的轴力弯矩相关曲线图,见图4。将有限元的计算结果一同绘制在图中,用实线表示有限元计算结果,虚线表示实用公式计算结果。长细比由上到下为43.2,62.1,86.9。

图4 有限元结果与公式结果对比图
由图4可见,在弯矩较小时随着长细比的增加,极限轴力出现下降,弯矩较大时长细比的影响减小。压弯实用计算公式与有限元分析的数据吻合较好,
表明推导出的实用计算公式可以用于此类十形闭口截面钢柱的稳定承载力验算。
3 结 语
根据有限元分析结果,可得以下结论:
1)有限元特征屈曲值和理论值吻合较精确,证明屈曲荷载理论推导正确。
2)长细比对十形闭口截面稳定承载力会产生一定的影响。当弯矩较小时长细比对承载力的影响较大;当弯矩增大时,长细比的影响减弱。
3)由有限元数据与本文推导出的实用公式对比,实用公式可用于此类十形闭口截面构件的稳定承载力验算。
[1]陈骥.钢结构稳定理论与设计[M].5版. 北京:科学出版社, 2011.
[2]朱俞江,童根树.箱形截面压弯构件的平面外稳定计算[J]. 钢结构, 2003(5):11-12.
[3]陈绍蕃.钢结构设计原理[M].3版. 北京:科学出版社, 2005.
[4]朱震华. 薄壁箱形截面双向偏心受压构件的试验与理论分析[D].西安:西安建筑科技大学,2010.
[5]王新敏.ANSYS工程结构数值分析[M].北京:人民交通出版社,2007.
Analysis of Global Stability on the Bended Units with Cross Closed Section
ZHAODiansheng,ZHENGShuheng
2016-04-07
赵滇生(1957—),男,浙江义乌人,副教授,研究方向为钢结构、空间结构。
TU375.3
B
1008-3707(2016)10-0004-04

