在数学试题探究中提炼模型获取通法
——利用“轴对称”求折线段和最小值问题探微
王斌(龙岩市初级中学,福建龙岩364000)
在数学试题探究中提炼模型获取通法
——利用“轴对称”求折线段和最小值问题探微
王斌
(龙岩市初级中学,福建龙岩364000)
利用“轴对称”求折线段和最小值问题,通过变式、引申、拓展等渠道,引导学生探究数学试题、提炼问题模型、获取通性通法,可以有效提升学生分析问题与解决问题的能力。
解题教学;模型提取;模型变式;模型拓展;题型概述
在数学中考复习中,提高学生的解题能力是解题教学的关键,就题讲题无法使学生的思维得到拓展,当学生再次遇到类似的题型仍然会无从下手。那么,在解题教学中,讲什么?如何讲?讲解的重点是什么?结合多年的教学反思,笔者认为要从学生实际和题目特点出发,有所取舍、有所侧重地进行解题教学讲解。下面,通过利用“轴对称”求折线段和最小值问题探微,谈谈以试题为源头,以模型为基础,通过变式来巩固,通过拓展来提升的方式,让学生获取解题通法,掌握解题技巧,提升解题能力。
一、题目呈现
题目:如图1,Rt△ABC中,∠C=900,AC=BC=4,E为边AC上一点,且CE长为1,若点P是斜边AB上的动点,求PC+PE的最小值。
从解题教学的策略来看,此题的讲解关键是引导学生如何提取与原题有关的模型(模型是学生所熟知的),通过分析,理解模型,进行恰当的变式和拓展,帮助学生理清这一类题型的思路,最终达到掌握解题的基本思想和基本技能。

二、模型提取
上述几何问题中的本源是什么?基本图形是什么?其实可以追朔到人教版(2013年)数学八年级上册中的课题学习:最短路径问题。
模型:如图2(1),直线同侧有两点A、B,要在直线上找一个点P,使PA+PB的和最小,请在图中找出点P的位置。

解析:如图2(2),作出点B关于的对称点B′,利用轴对称的性质,可以得到PB=PB′,这样,问题就转化为:当点P在的什么位置时,PA与P B′的和最小?在连接A,B′两点的线中,线段A B′最短,因此,线段AB′与直线的交点P的位置即为所求。我们可以进一步概括出此类题型的特点:两定点+一动点,且动点在直线上,两定点在直线的同一侧。其解决的方法就是:作一定点关于直线的对称点,连结对称点和另一定点的线段和直线的交点就是所求的,折线段和最短值就是这条连线段的长。
因此,教材中的例题、习题等往往是我们提取模型的重要素材。事实上,许多数学中考试题就是由这些题目中变式或拓展而来的。
三、原题解析
与模型相比,原题的背景变为三角形,但关键的特征和模型是一样的,所以我们可以利用模型方式解题(见图3):寻找C点或E点关于直线AB的对称点,此题中C点关于直线AB对称点较好确定,过C点作关于AB的对称点D,连结DE,DE交AB于点P,此时PC+PE的值最小,最小值为线段DE的长,连结AD,易知AD= AC=4,∠CAD=2∠CAB=2∠BAD=2×450=900,利用勾股定理:所以,PC+PE最小值为5。

四、模型变式
当学生探讨意犹末尽之时,趁热打铁,对原题进行变式,可以加深对原题认识的作用,进而培养学生在复杂的背景中抽取关键数学模型的能力,提升在实际背景下解决问题的能力。
变式一:如图4所示,正方形的面积为12,△ABE是等边三角形,点E在正方形ABCD内,在对角线上有一点,使PD+PE的和最小,则这个最小值为()
解析:此题与原题相类似,只不过一定点在正方形内,点D关于直线AC的对称点是B点,PD+PE=PB+PE,当P点为BE与AC的交点时,PB、PE的和最小,最小值为BE的长,因为△ABE是等边三角形,所以,故选A。

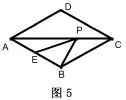
变式二:如图5所示,在菱形ABCD中,AB=2,∠BAD=60°,点E是AB的中点,P是对角线AC上的一个动点,则PE+PB的最小值为。
解析:此题与原题相比,背景变为了菱形,做法也是找一点(B点)关于动点所在直线的对称点(D点),易知△ABD为等边三角形,由E为AB的中点可得△ADE为直角三角形,∠DAE=600,求得DE=,所以PE+PB的最小值为。
变式三:如图6(1),长方体的底面长为5cm宽为4cm高为9cm,点A在长方体的棱边上且距长方体上沿3cm,点P为长方体上沿的动点,则在长方体侧面从点A到点P再到点C的最短路程为cm。

解析:沿点A所在的棱线展开,如图6(2)所示,点A到点P再到点C的最短路程实际上就是在直线MN上找一点P,使得PA+PC的值最小。作A关于直线MN的对称点A′,则PA=PA′,所以PA+PC=PA′+PC;当PA′+PC的值最小时,点P应为A′C与MN的交点,设A′C与MN相交于点为P′,此时P′A+P′C等于线段A′C,在Rt△A′BC中,A′B=A′M+BM=3+9=12 cm,BC=5+4=9 cm,A′C= 122+92=15cm,所以最短距离为15cm。
五、模型拓展
当学生经过模型的各种变式训练,已经掌握模型的精髓后,我们可进一步在原模型的基础上引导学生探索新的问题:前面我们研究的背景都是直线一侧有两个定点,直线上一动点问题,我们是否可以改变定点或动点的个数得到解题的通法呢?
1.“两定点+两动点”
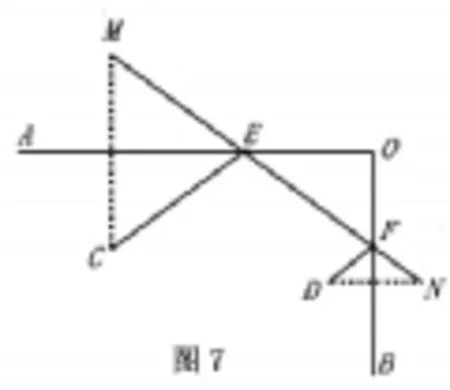
模型:如图7,C、D为定点,E、F分别为直线OA、OB上的动点,当EC+EF+FD最短时,请你确定点E、F的A′B2+BC2=位置。
解析:(1)作点C关于直线OA的对称点M,可得EC=EM;(2)作点D关于直线OB的对称点N,可得FD= FN,则EC+EF+FD=EM+EF+FN;(3)由两点之间线段最短可知:当EM+EF+FN=MN时,EM+EF+FN最短;此时,点E、F分别是MN交直线OA、OB的交点。
模型变式:如图8,在直线y=2x-4与抛物线y=2x2-x-3相交于点A、B(点A在点B的左侧),E点是抛物线对称轴上的动点,点F是轴上的动点,求四边形AEFB最短周长。
解析:(略)
2.三个动点
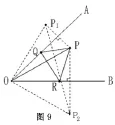
例:如图9,∠AOB=450,角内有一动点P,PO=10,在AO,BO上有两动点Q,R,求△PQR周长的最小值。
解析:作P关于OA,OB对称点P1,P2。于是有PQ+ QR+PR=QP1+QR+RP2≥P1P2,由对称性易知△P1OP2为等腰直角三角形,OP=OP1=OP2=10,P1P2=10。

六、题型概述
利用“轴对称”求折线段和最小值问题,通常是利用轴对称,把折线段和最短问题转化为两点之间线段最短问题,不管背景是正方形、菱形、圆、抛物线还是其它图形,我们要明确定点、动点和动点所在直线,并善于作出定点关于动点所在直线的对称点或动点关于其它动点所在直线的对称点。这样对这类问题的解决才可能事半功倍。
总之,进入中考复习阶段,我们要善于引导学生挖掘试题的模型、提炼模型解法,通过变式、引申、拓展等渠道提升学生分析问题,解决问题的能力。
[1]朱桂平.提取模型融会贯通——例谈中考压轴题的教学策略[J].中国数学教育(初中版),2014(7).
[2]胡云亚.由“将军饮马”引申的中考压轴题简析[J].数理化解题研究(初中版),2012(3).
[3]宋毓彬.用轴对称求线段和的最小值[J].数理化解题研究(初中版),2012(1).
(责任编辑:王钦敏)
——从广州一模的一道选择题谈起

