流场构建中径向基函数节点选取方法研究
黄家勇,张红梅,陈志高,朱世芳
(1.武汉大学 测绘学院,湖北 武汉 430079;2.武汉大学 动机学院,湖北 武汉 430072)
流场构建中径向基函数节点选取方法研究
黄家勇1,张红梅2,陈志高1,朱世芳1
(1.武汉大学测绘学院,湖北武汉430079;2.武汉大学动机学院,湖北武汉430072)
针对现有基于径向基函数的感潮河段局域时空流场模型构建中节点选取缺乏依据的现状,利用走航式ADCP资料研究了聚类算法、贪婪算法和梯度算法等3种节点位置选取方法,结合实验将3种不同节点位置选取方法下获得的余流场和潮流场与调和分析方法的结果进行对比分析,并采用交叉验证法评估节点选取方法构建模型。结果表明,3种节点选取方法各有特点,在实际应用中应根据不同的流场特点及工程需要选择合适的方法构建流场。
感潮河段;走航式ADCP;流场构建
感潮河段局域时空流场构建对于流速预报、流量计算、河道施工、流体动力学分析等意义重大(Wu et al,2013;单慧洁等,2015)。由于风应力、热通量、降水、蒸发、潮流、余流、地下水通量等对流速影响相对较小,且难以预测,感潮河段流速分析通常只考虑影响河口循环的主要因素潮流和余流,通过对流速观测数据调和分析得到余流和潮流调和常数构建流场模型。ADCP(Acoustic Doppler Current Profile,声学多普勒流速剖面仪)可以同时实现不同水深层的流速流向测量,测量速度快,在测量过程中不会对流场产生扰动,结合GPS和底跟踪技术(陈志高等,2013),可以快速获取流速的空间分布,实现大区域的高时间、空间分辨率流速测量,操作简单,是目前流速测量的主要手段(高菲等,2011;田淳等,2003)。
构建感潮河段局域时空流场的经典方法是基于内插点调和分析,实现局域流场构建。为了充分利用时间及空间分布不均匀走航测量数据,Candela等采用格林函数表示流速的平面分布,获得局域平面流场 (Candela et al,1992;张芩,2000);Münchow等(2000)将Candela方法扩展到三维流场构建;Vennell等(2006)采用以高斯函数为基函数的Candela方法实现了局域流场构建;黄奖等(2009)将径向基函数法应用于厦门湾断面重复走航;沈俊强等(2012)采用Candela方法分离厦门内湾东西口门海域潮流,分析潮流和余流特征。然而,已有研究常采用等间距点或格网点作为节点,均忽略了对径向基函数中节点位置及个数选取方法的分析及对比,而节点个数和位置对最小二乘解算的稳定及流场拟合的结果影响重大。为此,本文以高斯函数作为基函数,基于聚类算法、贪婪算法和梯度算法等3种节点选取方法构建流场模型,结合实验分析了3种节点选取方法的特点,以根据不同水域的流场特点选择最优方法,获得符合实际情况的最优时空流场。
1 局域流场构建模型
基于点内插调和分析是在走航起点和终点间等间距内插得到内插点,然后在每一个走航测次中,根据内插点附近的实际测量点进行反距离加权计算各内插点在该测次中的流速及对应的时间。得到内插点在每个测次中的观测值,然后对单点时间序列采用潮流调和分析公式计算潮流的调和常数,当数据序列较长时,调和分析具有较好的建模精度(方国洪,1986)。

式中,U(t)是t时刻某地点流速观测值,U0是潮流的余流值,m是调和分析所采用的分潮个数,Ui、ωi、θi分别是第i个分潮(i=1,…,m)的振幅、角速度、当地迟角。记

则上式可以写成

将内插点的时间序列代入上式,采用最小二乘即可解算出潮流调和常数和椭圆要素,实现潮流分离,通过测量区域内所有内插点的潮流调和常数可
以内插得到任意点的潮流调和常数,即可构建局域流场模型。
Candela等最早提出基于走航式ADCP资料的潮流分离方法是将测量流速中的余流和潮流调和常数表达为一组格林函数的线性组合,然后采用最小二乘法解算基函数中的系数实现局域流场模型构建,具有更好的空间相关性。本文采用以高斯函数为基函数的Candela法,也称为径向基函数法,将式中的U0、ai、bi用相同的形式F(X)表示。
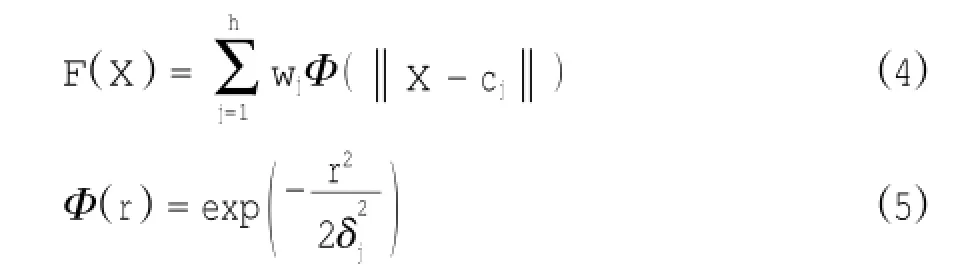


式中,w0为式中U0项对应的基函数权值矩阵,wCi,wSi分别是第i个分潮余弦项和正弦项对应的权值矩阵。
确定模型的基函数后,节点位置及其对应扩展系数的确定是模型解算的关键。本文采用聚类算法、贪婪算法和梯度算法等3种节点选取方法解算局域流场模型中节点位置、扩展系数、权值等参数。
1.1聚类算法
聚类算法是由Moody等(1989)提出的一种最经典的径向基函数(RBF)网学习算法。其思路是先对所有测量点进行聚类确定RBF网中h个节点的位置,并根据各节点之间的距离确定节点的扩展常数,然后采用最小二乘法计算流场模型参数。具体操作步骤如下:
(1)首先选择h个不同的节点初始位置,一般从测量点中随机选取或者等间距选取;
(2)计算所有测量点与每个节点的距离;
(3)对于所有测量点,按照最小距离原则分类到聚类域w1(k),w1(k),…,wh(k);
(5)如果前后两次计算得到的对应节点位置不再变化,则节点位置确定。否则,重复步骤(2)-(5);
(6) 根据式(6)计算潮流调和分析方程中的权值矩阵W,然后将W代入模型计算流速测量点对应的拟合流速U(Xi),进而计算得到模型内符合精度σh;
(7) 增加节点个数至h+1,重复步骤(1)-(6),直至得到对应的模型内符合精度σh+1。
聚类算法中各基函数具有统一的扩展系数

式中,dmax是所选节点之间的最大距离,h是节点的个数。
1.2贪婪算法
贪婪算法是由Vennel(2006)提出的一种径向基函数网络学习方法。贪婪算法根据模型拟合残差确定节点,将模型拟合效果最差点作为新增节点,使模型能够更好的拟合该点及附近测量点;然后再次拟合模型,根据拟合残差最大原则寻找下一个新增节点。贪婪算法基函数的扩展系数计算方法同式(7),确定径向基函数网络的节点位置步骤如下:
(1) 选取流速绝对值最大点作为初始节点加入节点集,根据式(6)计算权值矩阵W,并根据模型计算拟合流速U(Xi),得到各测量点的拟合误差ei=Ui-U(Xi);
(2) 将绝对值最大ei对应的测量点为作为新增节点加入节点集,然后将原有节点和新增节点代入式(6)重新计算模型参数及各测量点的拟合残差;
(3) 根据残差最大寻找新的节点,重复上述操作直至模型内符合精度σ不再减小,获得足够的节点数目。
当节点数目和坐标确定后,根据式(6)计算最终权值矩阵W,得到局域流场模型。
1.3梯度算法
梯度算法(Platt,1991)与BP算法训练多层感知器的原理类似,通过最小化目标函数E实现节点坐标及其对应的扩展系数、权值的调节。

其中,ei为测量点Xi的流速拟合残差,Ui为测量点Xi的流速测量值,U(Xi)为模型在点Xi处的Ui采样时刻的流速拟合值,P为总的测量点数。
若给定节点数h及其坐标(cj,x、cj,y)、扩展常数δj和权值wj的初值,为使目标函数最小,需分别对cj,x、cj,y、δj和wj求梯度,得到各自调节量。

式中,(Xi,x,Xi,y)为测量点Xi的平面坐标,η为学习率。
将测量数据代入式(10)-(13),求得各调节量,计算调整后的cj,x、cj,y、δj和wj。

将调整后的参数代入式(6),根据采样时刻及位置计算U(Xi),并与观测数据Ui比较,得到模型内符合精度。重复以上操作,直至相邻两次模型精度变化小于设定阈值,得到用于流场构建的径向基函数的最佳节点位置cj、扩展系数δj和权值wj及模型内符合精度σh。

2 实验与分析
2.1实验数据
为了检验3种节点选取方法构建流场的可靠性,实验选用徐六泾附近流域实测的走航式ADCP测量数据,实测流域是感潮河段,走航断面如图1(a)所示。走航式ADCP测量断面长度约为3.5 km,完成一次走航式测量耗时约20 min,每小时进行一次走航式测量,数据包含28次重复观测,总的测量时间长度超过一个日潮周期,重复观测过程中当前测次的测量终点是下一个测次的测量起点。走航观测恰逢秋季大潮期,观测得到的最大涨潮流速为1.38 m/s,最大落潮流速为1.85 m/s。数据中还包括测量区域附近锚定ADCP采样时间间隔为半小时,长达一个月的测量数据,通过对锚定ADCP测量数据进行频谱分析如图1(b),可以看出流域内主要分潮包括K1、M2、M4、M6、M8。根据Thomson等(2001)提出的最小频率分潮的周期应小于或等于观测资料的长度的调和分析分潮选取原则(Thomson et al,2001),而交叉验证部分建模数据长度为14 h,因此采用M2、M4、M6、M8等4个分潮。
2.2实验分析
2.2.1余流对比
利用调和分析方法及3种节点选取方法构建流场得到的余流在走航断面内插点上的分布如图2-图4所示,由于数据密度较大,每20个内插点取一个绘制到图上。图2(a)、图3(a)、图4(a)分别是调和分析方法与聚类算法、贪婪算法、梯度算法构建模型得到的余流对比。图中黄色带箭头矢量表示调和分析得到的余流,红色带箭头矢量表示流场模型计算得到的余流。调和分析得到的余流最大值为0.83 m/s,平均值为0.56 m/s。
从图2(a)、图3(a)、图4(a)这3幅图中可以看出,在内插点上调和分析得到的余流与本文3种不同节点选取方法下构建流场得到的余流大小和方向基本重合,在岸边和河道中间浅滩区域流场模型得到的余流与调和分析结果之间有一定偏差,这是因为调和分析各点单独解算,而本文方法对测量区域构建流场模型,具有更好的空间相关性。3种节点选取方法构建流场以及传统节点选取算法与调和分析方法得到余流的差值均方根见表1。从表中可以看出,传统节点选取方法构建流场模型与调和分析方法下余流误差均方根最大,贪婪算法具有整体最优,且节点位置确定比聚类算法合理,贪婪算法与调和分析得到的余流的误差均方根最小,仅为0.028 m/s。梯度算法具有局部最优,与调和分析计算得到余流较差的均方根最大,达到了0.055 m/s。
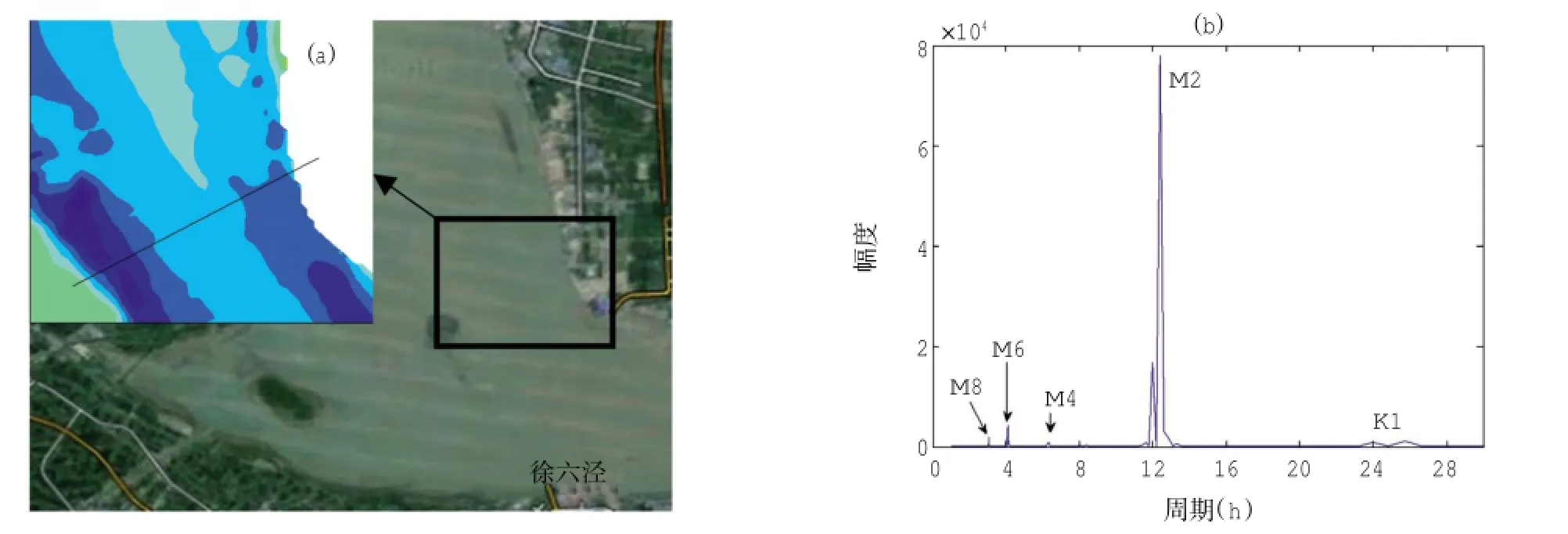
图1 测量断面位置及流速频谱分析
2.2.2潮流对比

图2 聚类算法与调和分析的余流(a)和M2潮流椭圆(b)对比(图中颜色条对应的刻度为河床的高程(下同))
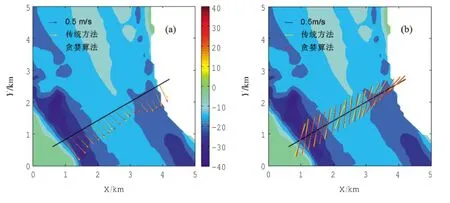
图3 贪婪算法与调和分析的余流(a)和M2潮流椭圆(b)对比
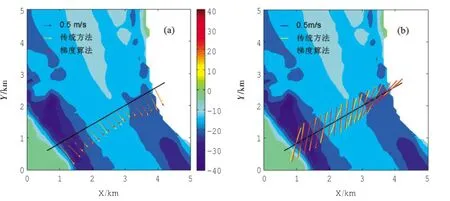
图4 梯度算法与调和分析的余流(a)和M2潮流椭圆(b)对比
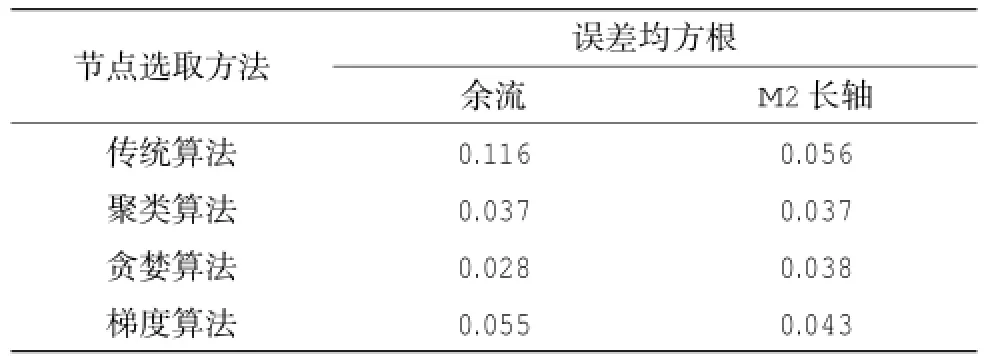
表13 种不同节点选取方法及传统节点选取方法下构建流场与调和分析得到余流和M2长轴的误差均方根
从图1(b)可以看出测量流域M2分潮振幅远大于其他3个分潮,因此这里只分析占主导地位的M2分潮潮流椭圆。将调和分析和3种节点选取方法构建流场模型模拟得到的结果在测量点上绘制出M2分潮潮流椭圆,如图2(b)、图3(b)、图4(b)。图中,黄色细线是调和分析得到的M2分潮潮流椭圆,红色细线是流场模型构建得到的M2分潮潮流椭圆。由于测量区域是近海感潮河段,潮流主要是沿河道方向,在垂直于河道方向上没有潮流波动,得到的潮流椭圆接近为一条直线。调和分析得到的M2潮流椭圆长轴最大值是1.16 m/s,平均值是0.98 m/s。3种不同节点选取方法下构建流场与调和分析计算的得到的M2潮流椭圆的长轴的误差均方根大小关系与余流较差均方根一致,且均小于调和分析计算值的5%。
从图2(b)、图3(b)、图4(b)可以看出,本文中3种不同节点选取方法下构建流场与调和分析相比得到的M2分潮潮流椭圆吻合较好,仅在河道中间的浅滩处有较大偏差。在天然河道中,流场变化较为平缓,而实验中调和分析得到的潮流椭圆在中间浅滩测点与相邻测点方向明显不一致,且该点所在区域水下地形没有明显变化。本文采用的Candela方法对区域内所有点整体解算,相邻点之间具有更好的空间相关性,所有内插点上M2潮流椭圆长轴具有比较一致的变化趋势,计算结果符合天然河道流速变化规律。
2.2.3模型验证
为了进一步验证模型的可靠性,将28个测次的数据分成两个部分,前14个测次数据作为实验组,采用本文3种不同节点选取方法以及传统节点选取方法分别构建流场模型;后14个测次数据作为验证组,用来验证实验组构建的局域流场模型的可靠性。分别用流场模型模拟实验组和验证组数据与测量数据对比计算模型的内符合精度和外符合精度,得到的模型验证结果如表2。
从表2中可以看出,传统节点选取方法的内符合精度和外符合精度都是最差的。聚类算法的内符合精度较好,而外符合精度较差,达到了0.257m/s。由于聚类算法节点选取只与测量位置分布有关,不能反映流速特征,具有整体最优性,因此内符合精度较好,而外符合精度较差。梯度算法具有较差的内符合精度,因为梯度算法中目标函数最小同时顾及了节点位置、扩展系数和权值,具有局部最优,因此得到的内符合精度比其他3种节点选取方法差,但是构建的模型更接近真实值,得到了较好的外符合精度0.202 m/s。实验中贪婪算法具有最好的内符合精度和外符合精度,因为本文所用数据中为走航断面的重复测量,采样点分布密集,流速的空间变化不大,且测量数据质量较好。计算过程中,聚类算法和贪婪算法的运算速度较快,而梯度算法耗时长。对于本文实验数据,贪婪算法比较适用;如果对运算速度没有要求,梯度算法同样适用。

表2 3种不同节点选取方法及传统节点选取方法下构建流场的内外符合精度对比(单位:±m/s)
3 结语
(1) 聚类算法计算简单,运算速度快,但节点选取只与点位分布相关。贪婪算法不需要先验参数,但节点均为测量点且节点位置不会随着个数的增加变化,易受测量粗差和采样密度影响。梯度算法根据待求参数的梯度不断调整参数值,节点和参数均满足内符合精度最小,避免了病态矩阵造成的不稳定解问题,稳定性更好,但运算速度慢,受参数初值影响较大。
(2) 基于径向基函数的感潮河段局域时空流场构建中,聚类算法适用于测量精度较差、区域内流速的空间分布变化不大的流场构建,贪婪算法适用于密集采样且测量精度高的走航数据构建流场,梯度算法适用于运算速度要求不高的流场构建。在应用中可根据需求选用合适的节点选取方法构建流场模型。随着测量区域的增大以及水文条件的变化,3种节点选取方法构建流场模型的适用性以及模型的空间和时间外推能力有待进一步的验证。
Candela J,Beardsley R C,Limeburner R,1992.Separation of tidal and subtidal currents in ship-mounted acoustic Doppler current profiler observations.Journal of Geophysical Research:Oceans(1978-2012),97:769-788.
Moody J,Darken C J,1989.Fast learning in networks of locally-tuned processing units.Neural computation,1:281-294.
Münchow A,2000.Detiding Three-Dimensional Velocity Survey Data in Coastal Waters.Journal of Atmospheric and Oceanic Technology, 17(5):736-748.
Platt J,1991.A resource-allocating network for function interpolation. Neural computation,3:213-225.
Thomson R E,Emery W J,2001.Data analysis methods in physical oceanography.Newnes.
Vennell R,Beatson R,2006.Moving vessel acoustic Doppler current profiler measurement of tidal stream function using radial basis functions.Journal of Geophysical Research:Oceans(1978-2012), (111):275-278.
Wu H,Deng B,Yuan R,et al,2013.Detiding measurement on transport of the Changjiang-derived buoyant coastal current.Journal of Physical Oceanography,43:2 388-2 399.
陈志高,张红梅,赵建虎,2013.基于GPS的ADCP流速和流量精确确定方法.中国矿业大学学报,42:670-675.
单慧洁,张钊,汪一航,等,2014.温州鳌江近海建设工程环境影响潮汐潮流数值模拟.海洋通报,(3):250-258.
方国洪,1986.潮汐和潮流的分析和预报.海洋出版社,58-63.
高菲,周根富,姜志成,等.2011.ADCP技术在河流流量测验中的应用.江苏水利,(1):27-29.
黄奖,葛勇,2009.船载ADCP资料的潮流分离方法在厦门港断面重复走航中的应用.台湾海峡,28:123-129.
沈俊强,潘伟然,张国荣,等,2012.基于三维调和分离的同安湾口门断面冬季潮流和余流特征的分析.台湾海峡,31:338-344.
田淳,刘少华,2003.声学多普勒测流原理及其应用.黄河水利出版社.
张芩,2000.船载ADCP资料的潮流分离技术.海洋通报,19:49-55.
(本文编辑:袁泽轶)
Study on the method of selecting optimal centers in the construction of local flow field based on the radial basis function
HUANG Jia-yong1,ZHANG Hong-mei2,CHEN Zhi-gao1,ZHU Shi-fang1
(1.School of Geodesy and Geometics,WuhanUniversity,Wuhan 430079,China; 2.School of Power and Mechanical Engineering,Wuhan University,Wuhan 430072,China)
In terms of the current situation that there is a lack of center selecting method in the flow field construction of tidal reach using radial basis function(RBF),three methods of selecting optimal centers,including clustering algorithm, greedy algorithm and gradient algorithm,are studied to construct flow field based on ship-mounted Acoustic Doppler Current Profiler(ADCP)data in this paper.The residual and M2 tidal ellipse of the constructed flow filed and traditional harmonic analysis are contrasted.The performance of flow field is assessed by cross-validation technique.Results show that the practical requirement of construct flow filed should be taken into consideration to choose the optimal selecting method due to the three methods of selecting optimal centers having respective characters.
tidal reach;ship-mounted ADCP;flow field construction
P731.2
A
1001-6932(2016)05-0516-07
10.11840/j.issn.1001-6392.2016.05.005
2015-07-07;
2015-09-07
国家自然科学基金(41576107;41376109;41176068);国家重大专项(2016YFB0501703)。
黄家勇(1991-),男,硕士研究生,主要从事水文水资源相关的研究。电子邮箱:huangjiayong@whu.edu.cn

