土石坝有限元分析中的应用接触单元法在混凝土心墙

王桔

（湘潭市水利水电勘测设计院　湘潭市　411100）

土石坝有限元分析中的应用接触单元法在混凝土心墙

王桔

（湘潭市水利水电勘测设计院湘潭市411100）

为研究混凝土心墙土石坝中混凝土心墙与土石坝坝体之间的摩擦接触对心墙、坝体应力应变的影响，文章以某混凝土心墙土石坝为例，采用ANSYS有限元分析软件建立二维模型，引入点点接触单元模拟混凝土心墙与其周围土体间的接触问题，研究了心墙与坝体的受力特性，并将其与不考虑心墙与坝体之间摩擦接触的情况比较。结果显示，点点接触单元可以模拟心墙及其周围土体间的接触面，且引入接触单元后，心墙、坝体的受力均减小，运行期心墙的受力减小最明显。

接触单元土石坝混凝土防渗墙应力

引言

许多学者和专家对土石坝中防渗墙的应用作了大量的研究，但是在研究过程中，他们大多没有深入考虑防渗墙与坝体之间的接触问题。实际上，混凝土防渗墙与其周围土体之间存在着起固壁作用的泥浆，它具有一定的塑性和徐变性能，不考虑土体材料与混凝土材料间的接触，也就忽略了泥浆固壁对混凝土防渗墙墙体受力的影响。为研究混凝土心墙土石坝的实际应力情况，有必要引入一种方法考虑心墙与其周围土石坝坝体之间的摩擦接触问题，据此，本文根据接触单元的力学机理，引入点-点接触单元，基于某心墙土石坝，对该心墙土石坝进行有限元分析。

1 接触单元的力学机理

1.1接触单元的选择

在有限元分析中，通常在两种材料接触面上设置接触单元［1～2］来模拟接触面上应力状况。有限元分析中常用的接触单元类型主要有以Goodman单元［3］为代表的无厚度单元和以Desai单元［4］为代表的有厚度单元。薄层单元的厚度难以取到合适的值，且带厚度的单元在有限元分析软件中也不容易应用，而Goodman单元类型能够较好模拟接触面的错动与张开，且单元参数相对容易确定，本次选用无厚度单元进行分析。ANSYS支持的无厚度度单元包括面-面、点-面、点-点接触三类［5］。面-面接触单元只支持一般的静态或瞬态、屈曲、模态、子结构或谱分析问题；点-面接触单元不适用于不光滑连续的接触。本文选取点-点接触单元CONTAC12。

1.2模拟接触面的模型选择

ANSYS软件处理接触面模拟问题时，需要采用合理的模型进行模拟。有限元分析中通用的模型包括等效连续模型、接触单元模型及接触边界模型。等效连续模型采用的连续性假设将导致参数定义困难和几何模型过于简化；接触单元模型适用范围有所限制，对精度也有一定影响［6］；接触边界模型往往需要进行多次迭代求解，对计算能力的要求比较高。当今电子计算机的快速发展，这种计算能力的要求是不难实现的，本次选用接触边界模型。

1.3接触单元的力学机理

取接触面单元由两片长度为L的接触面12和34组成，假设两片接触面之间由无数微小的弹簧连接。在受力前两接触面完全重合，即单元没有厚度只有长度，是一种一维单元，并令两相邻接触单元之间，只在结点处有力的联系。每片接触面两侧有两个节结点。一个单元共有4个结点。

在结点力｛F｝e作用下，两接触面间的弹簧受内应力为：

相应的在两片接触面之间产生相对位移：

角标s表示切向，n表示法向。

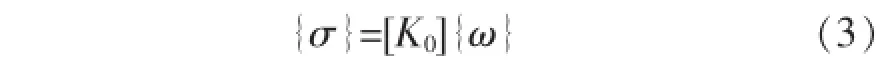
在线性弹性假定下，应力｛σ｝与相对位移｛ω｝成正比，写成关系式为：，ks、kn分别为切向及法向的单位长度刚度系数（N/m3）。对于弹性材料为常量，若材料具有非线性特征，视为变量。

取线性位移模式，把每一片接触面上沿长度方向各点的位移表示为结点的位移，用u、v分别表示为x、y方向上的位移，则顶面及底面的位移分别为：

接触面单元内各点的相对位移为（取压为正）：

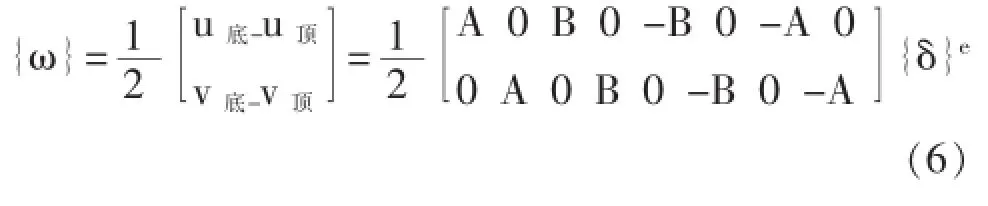
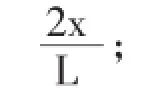
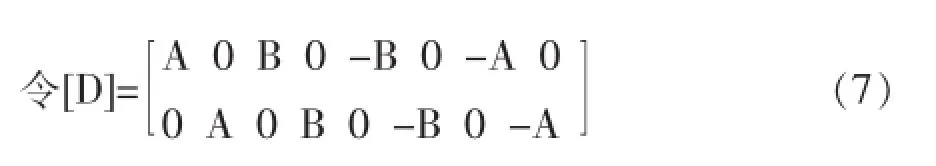
上式可写成

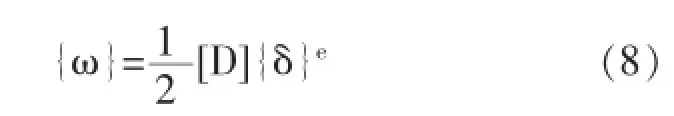
由虚位移原理推得：

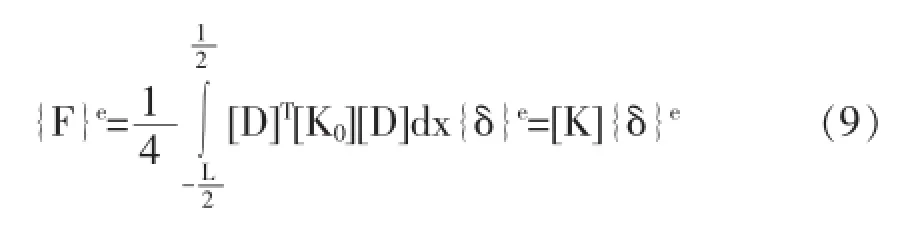
式中

式中L——接触单元的长度；

kn——法向模量。

以上刚度矩阵是在标准坐标系下建立起来的，而实际上接触面不一定是水平的，这就需要进行坐标系的转化。取接触面仰角β，则局部坐标系与整体坐标系存在如下关系：

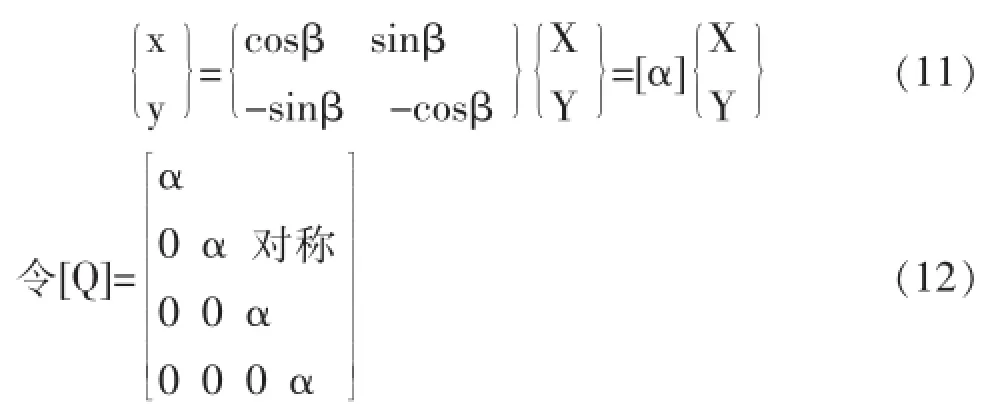
则结点力和结点位移的局部坐标系与整体坐标系间有如下关系：

｛F｝e=［Q］｛F¯｝e，｛δ｝e=［Q］｛δ¯｝e（13）

F¯和δ¯分别表示整体坐标的结点力和结点位移。将式（1）～式（13）代入式（1）～式（9），即可得到用整体坐标系表示的劲度关系：

｛F¯｝e=［Q］-1［k］［Q］｛δ¯｝e=［k¯］｛δ¯｝e（14）在由｛δ¯｝e求应力时也应作坐标变化。

1.4ANSYS接触迭代算法

在有限元分析计算中，进行接触迭代的算法比较多，主要包括求解带约束的泛函极值问题的方法、数学规划的线性补偿方法、直接求解的方法等。本文问题涉及到要实现接触面上接触力的传递以及接触面没有穿透，这两点必须在接触面的法向方向上实现。在用有限元软件分析中，这两点通常用求解带约束泛函极值问题的方法来完成，带约束的泛函极值问题的求解方法主要分为罚函数法，拉格朗日乘子法及推广拉格朗日乘子法等［5］。

拉格朗日乘子法的刚度矩阵中有可能存在零对角，选择求解器就会受一定的限制，且随着自由度的增加，刚度矩阵有所增大，计算也就变得更加复杂；推广拉格朗日乘子法需人为定义ANSYS中的TOLN（最大穿透值）值来确定接触面允许的最大穿透值［7］，与罚函数法相比，它的迭代次数可能会更多。本此采用罚函数方法迭代求解。

2 接触单元在混凝土心墙土石坝中的应用

2.1工程概况

本工程实例为某一加固病险粘土心墙土石坝。大坝典型横断面及坝体各特征数值见图1，为简化计算，本文将典型断面近似看成对称面。该土石坝已经运行近40年，坝基沉降基本趋于稳定。此次加固是通过在粘土心墙中修建混凝土防渗墙的措施来解决坝体严重的渗漏问题，防渗墙沿坝轴线布置，墙厚0.6m，深入基岩1.0m，加固后横断面见图2。

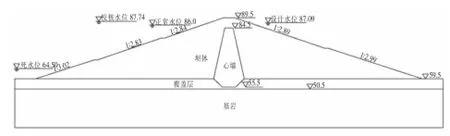
图1　大坝加固前典型横断面图

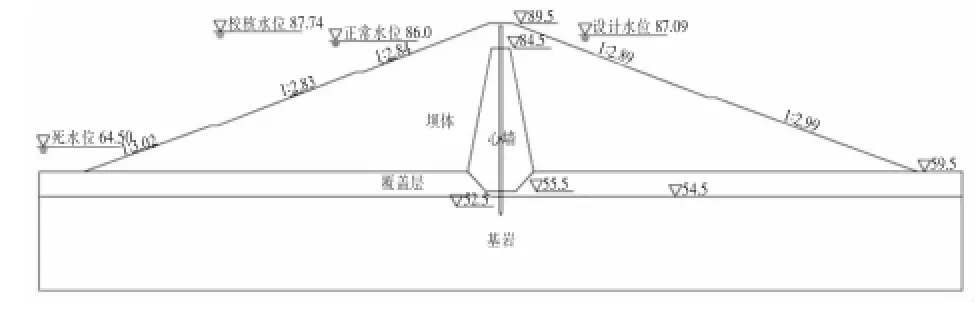
图2　大坝加固后典型横断面图

2.2模型及参数选择

（1）模型及网格划分。

根据典型断面建立二维模型（见图3），此次计算中，土料及混凝土心墙均采用plane42单元，混凝土与土体间接触问题采用CONTAC12接触单元模拟。以水平向为X轴方向，指向坝体下游面为正；竖直向为Y轴向，向上为正；Z轴垂直纸面（Z≈0）。用四节点四边形及少数的三节点三角形单元划分模型，模型共划分为6个单元组，1377个平面单元，1 554个节点及60个接触单元。考虑到防渗墙所受周围土体之间的摩擦约束主要在坝基面以上，故接触单元设置在坝基面以上防渗墙与土体接触处。为了能更好的应用点点接触单元，在墙体与周围土体相接处的网格应尽量趋于一致。

图3　大坝网格划分图

（2）模型材料参数及计算方案。

模型材料分为坝壳、粘土心墙、覆盖层、基岩及混凝土防渗墙五种材料，材料参数根据相关实例确定［8～10］，如表1所示。

表1　模型材料参数表

本次按工况①：防渗墙竣工期；工况②：防渗墙正常运行期两种工况分别对混凝土心墙坝考虑接触问题和不考虑接触问题，即有、无引入接触单元（分别为方法一、方法二）进行平面应力分析。后一工况的计算将以前一工况的应力场作为初始条件，而将模型仅在坝基（坝基沉降近似趋于稳定）土体重力荷载下并分六次加载坝体重力计算得出的应力场作为工况①的初始应力场，水荷载一次加载。此外，计算模型中，粘土心墙、坝壳材料采用Duncan-ChangEB模型，坝基与防渗墙看作线弹性模型，并借助ansys软件进行计算。

2.3计算结果

2.3.1初始应力场

在坝基（坝基沉降近似趋于稳定）土体重力荷载下并分六次加载坝体重力计算得坝体水平向及竖直向位移变形云图如图4。

图4　水平及竖向位移变形云图

由图4可知，坝体水平位移和垂直位移沿坝轴线基本成对称分布。水平位移在土体自重的作用下，上游部分水平位移指向上游，下游部分水平位移指向下游，最大水平位移为2.14cm。垂直位移自坝体两坡面向坝体心墙逐步增大，坝体最大沉降为20.89cm，最大沉降发生坝体中部，约1/2坝高处。坝体变形符合一般土石坝受力变形规律［11］，故ANSYS能实现有限元中土体非线性邓肯张E-B模型的加载。

2.3.2防渗墙竣工期应力情况

有、无引入接触单元求得坝体及墙体水平及竖直向应力情况见表2。

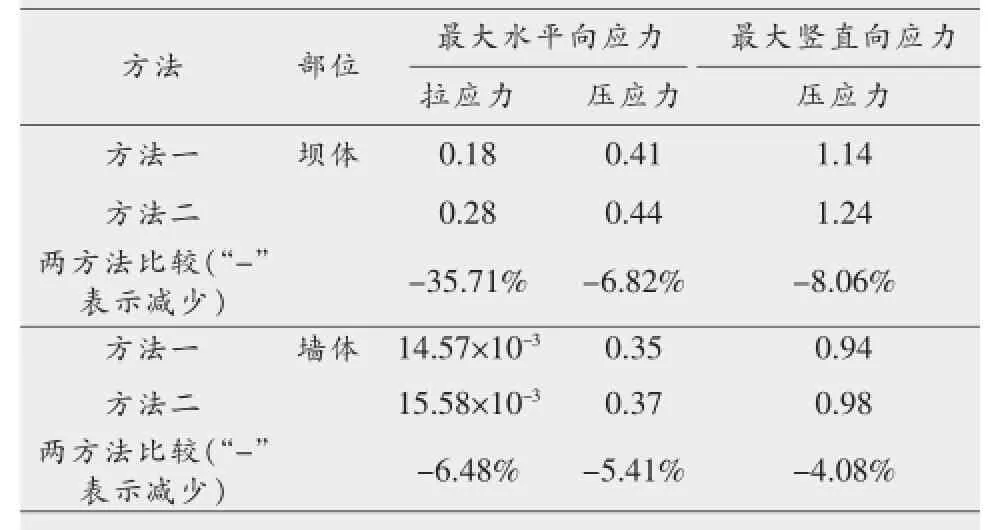
表2　防渗墙完工期坝体及墙体水平及竖向应力情况MPa

从Ansys计算云图可以看出两种方法坝体的最大应力分布情况基本一致，最大竖向压应力均发生在坝基中央附近。两种方法计算得出的防渗墙应力沿高程分布情况见图5、图6。

2.3.3防渗墙正常运行期应力情况

在水荷载、围土挤压及基岩约束下，两种方法求得坝体及墙体水平及竖直向应力情况见表3。

两种方法计算得出的防渗墙应力沿高程分布情况见图7、图8。

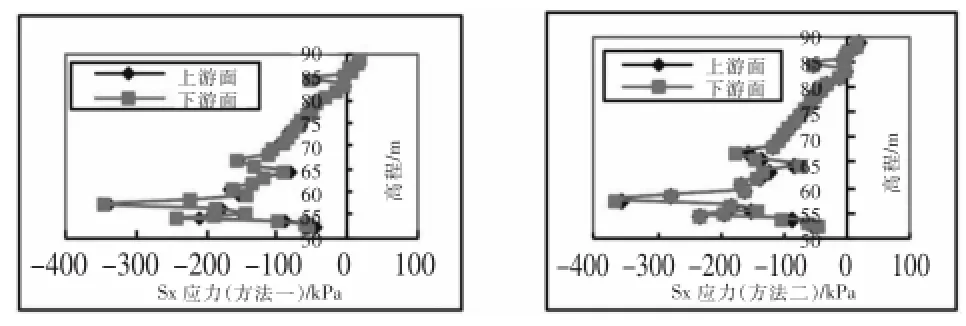
图5　防渗墙竣工时水平应力Sx沿高程变化

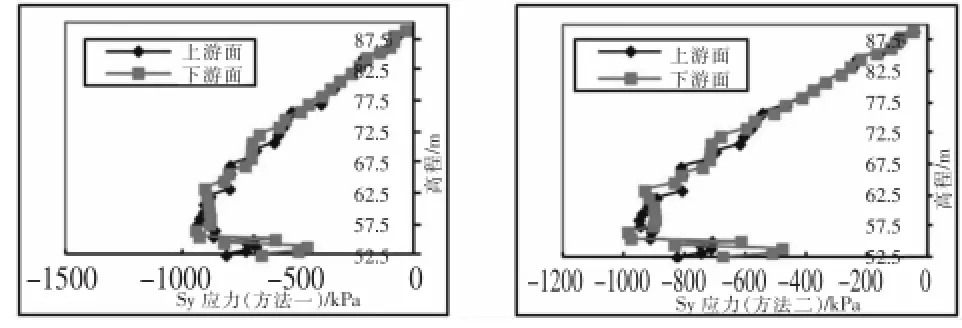
图6　防渗墙竣工期墙体竖直应力Sy沿高程变化

表　3　防渗墙运行期坝体水平及竖向应力情况　MPa

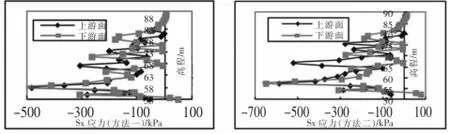
图7　防渗墙运行期墙体水平应力Sx随高程变化情况

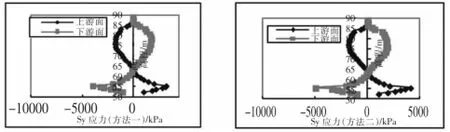
图8　防渗墙运行期墙体竖直应力Sy随高程变化情况

此外，两种方法两种工况下第一主应力与第三主应力的最大值情况见表4。

由表2～表4及图2～图8，点-点接触单元可以来模拟混凝土防渗墙与其周围土体之间的接触问题。引入接触单元后，两种工况下计算得出防渗墙、坝体所受的应力均小于未引入接触单元时求得的应力，防渗墙表现得更为明显。运行期较竣工期减少量更明显，水平向应力较竖直向应力减少量更大，最大可以减少38.0%。

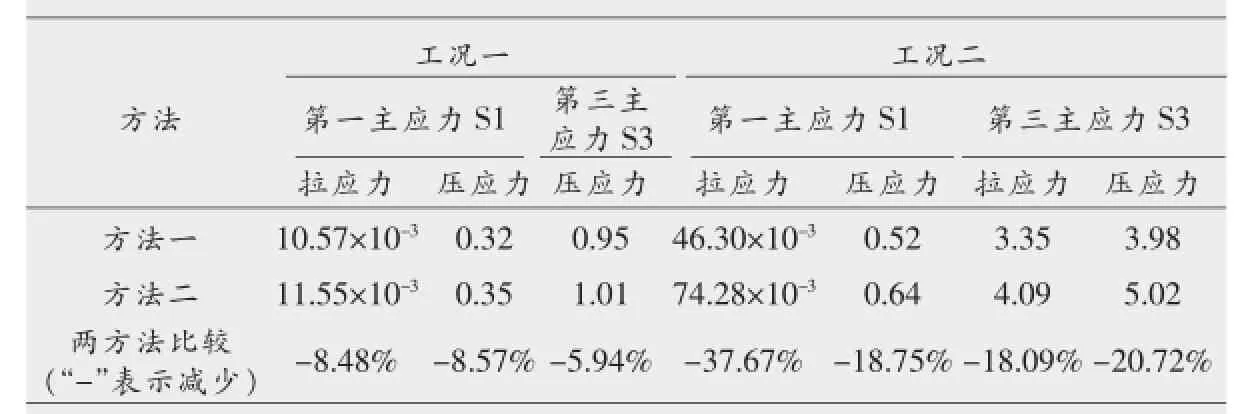
表4　防渗墙竣工期及运行期墙体最大主应力情况　MPa

3 结　论

本文借助有限元软件ANSYS，引入接触单元对混凝土心墙土石坝进行有限元分析，主要结论如下：

（1）接触单元可以实现力在不连续位移间的传递，将它引入到有限元分析中，是比较符合墙体实际受力情况的。

（2）当引入接触单元考虑防渗墙与坝体之间的接触面问题时，心墙及坝体计算得出的应力均小于未引入接触单元时计算得出的应力，防渗墙表现更为明显，且运行期受水荷载作用，应力减少更大，此外，运行时期的防渗墙水平向拉应力表现最突出，减少量达38%。

［1］Clough G W， Duncan J M. Finite element analysis of retaining wall behavior ［J］. Journal of the Soil Mechanics and Foundations Division，1971， 97（12）： 1657-1673.

［2］安关峰，高大钊.接触面弹粘塑性本构关系研究［J］.土木工程学报，2001（1）：88-91.

［3］Goodman R F， Tayor R L， Brekle T L.A model for the mechanics of jointed rock ［J］. Journal of Soil Mechanics and Foundation Engineering Division， 1968， 94 （3）： 637-660.

［4］Desai C S， Zaman M M， Lightner J G， et al. Thin layer element for interfaces and joints ［J］. International Journal for Numerical and Analytical Methods in Geomechanics， 1984， 8 （1）： 19-43.

［5］刘涛，杨凤鹏.精通ANSYS［M］.北京：清华大学出版社，2002.

［6］张楚汉，金峰.岩石和混凝土离散-接触-断裂分析［M］.北京：清华大学出版社，2008.

［7］王伟，卢廷浩，宰金珉，等.土与混凝土接触面反向剪切单剪试验［J］.岩土力学，2009，（5）：1303-1306.

［8］路阳.土石坝加固中混凝土防渗墙应用研究［D］.武汉：武汉大学，2010.

［9］刘娜.土石坝三维非线性有限元分析及防渗墙应力状态研究［D］.西安：西安理工大学，2007.

［10］华东水利学院力学教研室主编.土工原理与计算.上册［M］.北京：水利电力出版社，1982.

王桔（1985-），女，硕士研究生，工程师，主要从事水利工程设计工作，手机：18273223164，E-mail：wj_whu@yeah.net。

［11］陈慧远.土石坝有限元分析［M］.南京：河海大学出版社，1988.（2016-07-11）