四旋翼飞行器极点配置姿态控制器设计

肖 勇,孙志毅

(太原科技大学，太原 030024)



四旋翼飞行器极点配置姿态控制器设计

肖 勇,孙志毅

(太原科技大学，太原 030024)

针对四旋翼飞行器姿态控制系统具有多变量、干扰敏感、强耦合等特性，将飞行器动力学模型在平衡点处线性化，在满足超调量和调节时间性能指标的情况下，采用了状态反馈极点配置将系统闭环极点配置在期望的位置上，从而实现飞行姿态的平稳控制。为了检验所述算法，通过Matlab软件设计了极点配置控制器，并实现了在四旋翼飞行器实验平台上的稳定控制，证明了该控制算法的有效性及稳定性。

四旋翼飞行器；姿态控制；极点配置

四旋翼飞行器一直是小型无人飞行器的研究热点，它具备起落空间需求少、飞行姿态灵活等性能，所以非常适合在有限的空间内进行作业，包括用于空中测绘、消防救援、农业等方面。飞行器姿态控制系统是一个具有多自由度和多控制输入的欠驱动系统[1]，其动力学系统具有多变量、非线性、强耦合和干扰敏感的特性，使得飞行控制系统的设计变得非常困难。因此，飞行器姿态控制问题在理论和工程应用上都是具有重要探索意义的研究课题。

文献[2]提出运用自适应逆控制方法进行四旋翼飞行器姿态稳定控制，该方法有效地减少噪声和扰动的影响因素，对系统鲁棒性有一定的提高。文献[3]针对四旋翼姿态控制设计了鲁棒自适应反步控制器来抵消干扰和参数不确定性等因素。但上述方法都存在控制器模型较为复杂，控制率计算繁琐等，在实际应用中易产生系统时间上的延迟。

本文以四旋翼飞行器姿态控制问题为应用背景，采用具有计算简单、动态响应迅速等优点的状态反馈极点配置控制器，通过Matlab仿真软件设计了极点配置控制器将系统闭环极点配置在期望位置上，实现四旋翼飞行器姿态的平稳控制，最后在实验平台上成功应用，进一步验证了姿态控制系统的控制效果及其可行性[4-5]。

1 四旋翼飞行器动力学建模

建立如图1所示OXYZ坐标系。其中，坐标原点位于支撑点O，指向正前方电机的轴为X轴，指向右侧电机的轴为Y轴，采用左手定则确立坐标系Z轴。其中，前向、左侧和右侧电机转动带动螺旋桨运动产生的力Ff、Fl、FY、与Z轴同向为正向。尾部电机转动带动螺旋桨运动产生的力FS，与Y轴同向为正向。

为了便于动力学分析及建模，本文对控制对象做出如下假设：

(1)假设系统为刚体，忽略系统摩擦力、电机阻尼转矩；

(2)假设系统左右部分完全对称，质心在几何中心O；

(3)忽略伺服电机达到给定转速的时间；

(4)假设螺旋桨在转动过程中固定不可形变。

俯仰角θ：飞行器与OXY平面的夹角；

横滚角：δ飞行器与OYZ平面的夹角；

偏航角：φ飞行器与OXZ平面的夹角；

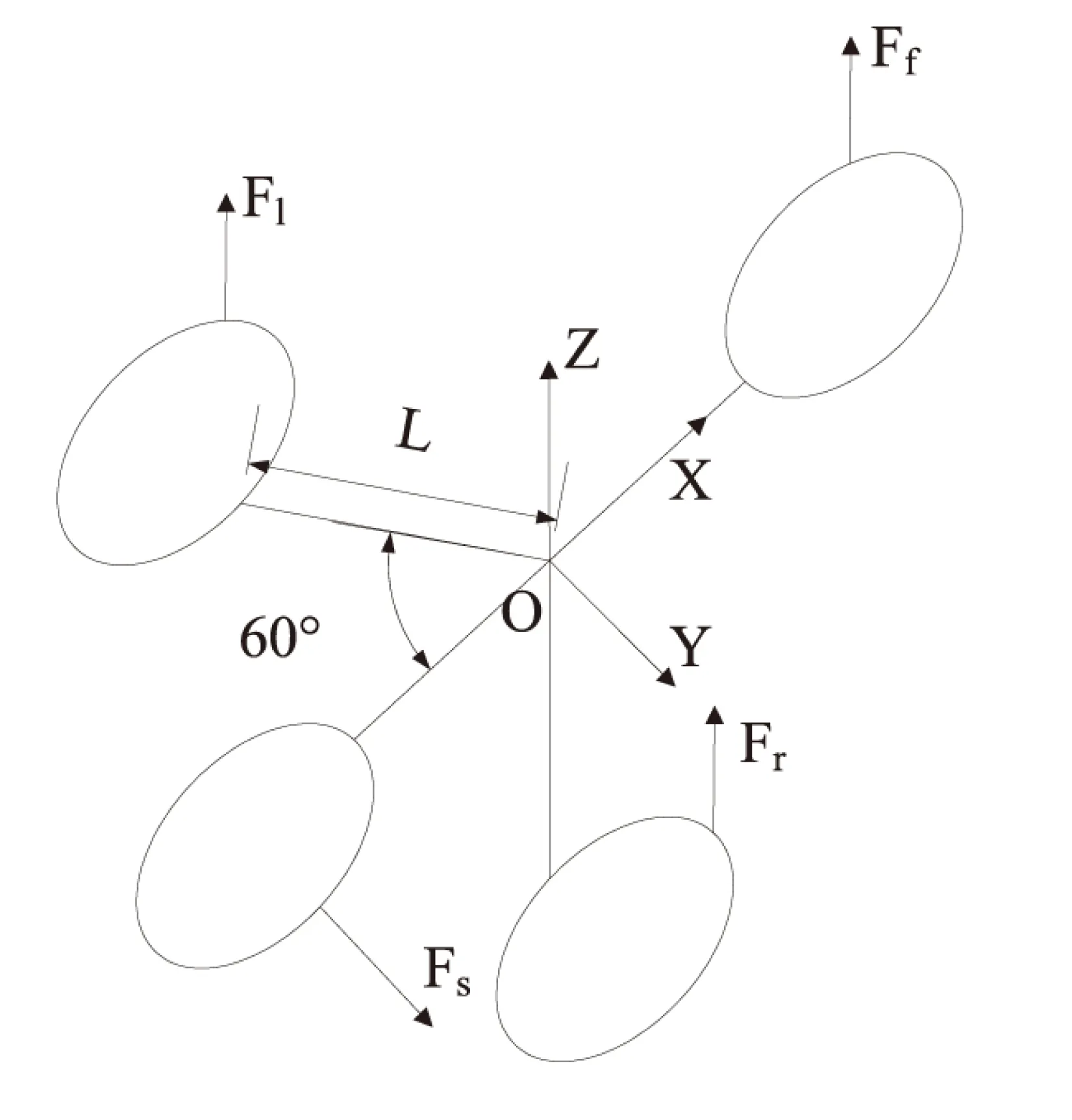
图1 四旋翼飞行器受力分析图

针对飞行器关键受力和力矩，并忽略系统摩擦力、电机阻尼转矩，通过受力分析，然后根据牛顿定律和欧拉方程通过化简可推导出四旋翼飞行器非线性动力学微分方程组：

(1)

其中，Lf为支撑点O到各个旋翼的长度，左侧与右侧电机于X轴之间的夹角为60°.vf、Ff为前向电机电压及产生的升力，vl、Fl为左侧电机电压及产生的升力，vr、Fr为右侧电机电压及产生的升力，vs、Fs为尾部电机电压及产生的力，Jθ、Jδ、Jφ分别为三个姿态角的转动惯量，k为电压升力比。

2 四旋翼飞行器极点配置控制器设计

为了分析方便并得到解析解，需要对方程组进行必要的线性化处理。由于控制的目的是保持四旋翼飞行器稳定于平衡状态，即飞行器三个姿态角θ、δ、φ趋近于0，此时，令sinα≈0，cosα≈1，代入式(1)整理得到线性化后的四旋翼飞行器姿态控制系统状态方程为：

(2)

式中，

由于系统闭环极点的复平面分布情况决定了系统的稳定性和动态性能，而状态反馈极点配置的含义是，以一组期望极点为动态性能指标，根据极点配置定理推导出使控制系统特征值匹配到复平面期望位置的状态反馈控制参数，从而达到系统对动态性能的要求。

式(2)状态方程通过计算可知：rankUc=6.

即系统状态完全能控，所以四旋翼飞行器姿态控制系统∑(A,B,C)是能实现任意极点配置的。

对于四旋翼飞行器姿态控制系统，本文主要参考两个时间域性能指标进行设计：

超调量：

(3)

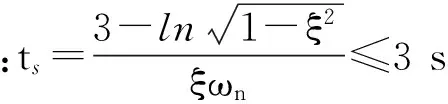
(4)

计算式(3)与(4)，可得出四旋翼飞行器姿态控制系统的的两个主导极点为：

λ1,λ2=-1.73±1.4j

对于其他4个非主导极点，可以在左半s平面远离主导极点对的区域内任意选取，其区域右端离虚轴的距离至少等于主导极点对虚轴距离的3到6倍，本文取为λ3,λ4=-5，λ5,λ6=-6.

3 实验结果与分析

实验所采用的四旋翼飞行器，其硬件系统组成框图如图2所示，计算机经过PCIE-PCI转接卡与运动控制板卡相连，它用安装在平台上的三个编码器检测飞行仿真器的俯仰角、横滚角、偏航角的实时数据，然后通过运动控制板卡反馈入控制器计算四个电机的控制量——电机电压，并驱动相应的电机运动，带动螺旋桨产生升、降力，从而达到稳定控制的目的。

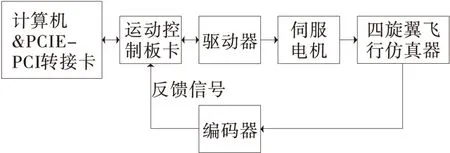
图2 四旋翼飞行器硬件系统组成框图

其中，四旋翼飞行器硬件平台物理参数如表1所示：

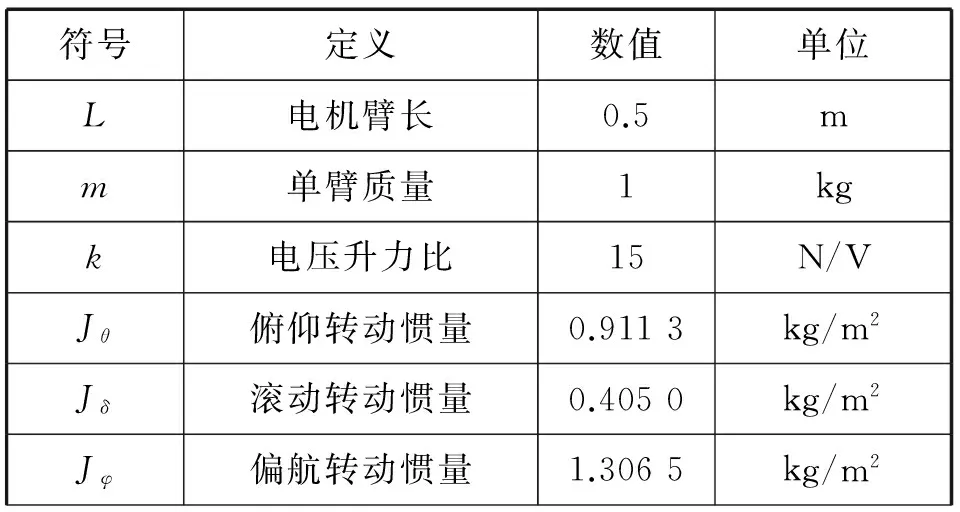
表1 四旋翼飞行器硬件平台物理参数

将表1数据代入式(2),计算得到反馈增益矩阵K结果如下：

K=

为了对飞行器姿态控制系统进行仿真实验，本文采用MATLAB软件进行仿真设计[6-7]，通过仿真可以得到整个四旋翼姿态控制系统的仿真输出情况如图2所示，其中，横坐标轴为T/s，纵坐标轴为angle/°，给定曲线为正弦信号。由图3可以看出，系统的输出响应及跟踪效果反映出了极点配置控制器良好的控制效果，其静态误差很小，动态性能都能达到控制要求，由此可以看出极点配置控制算法的有效性和稳定性。

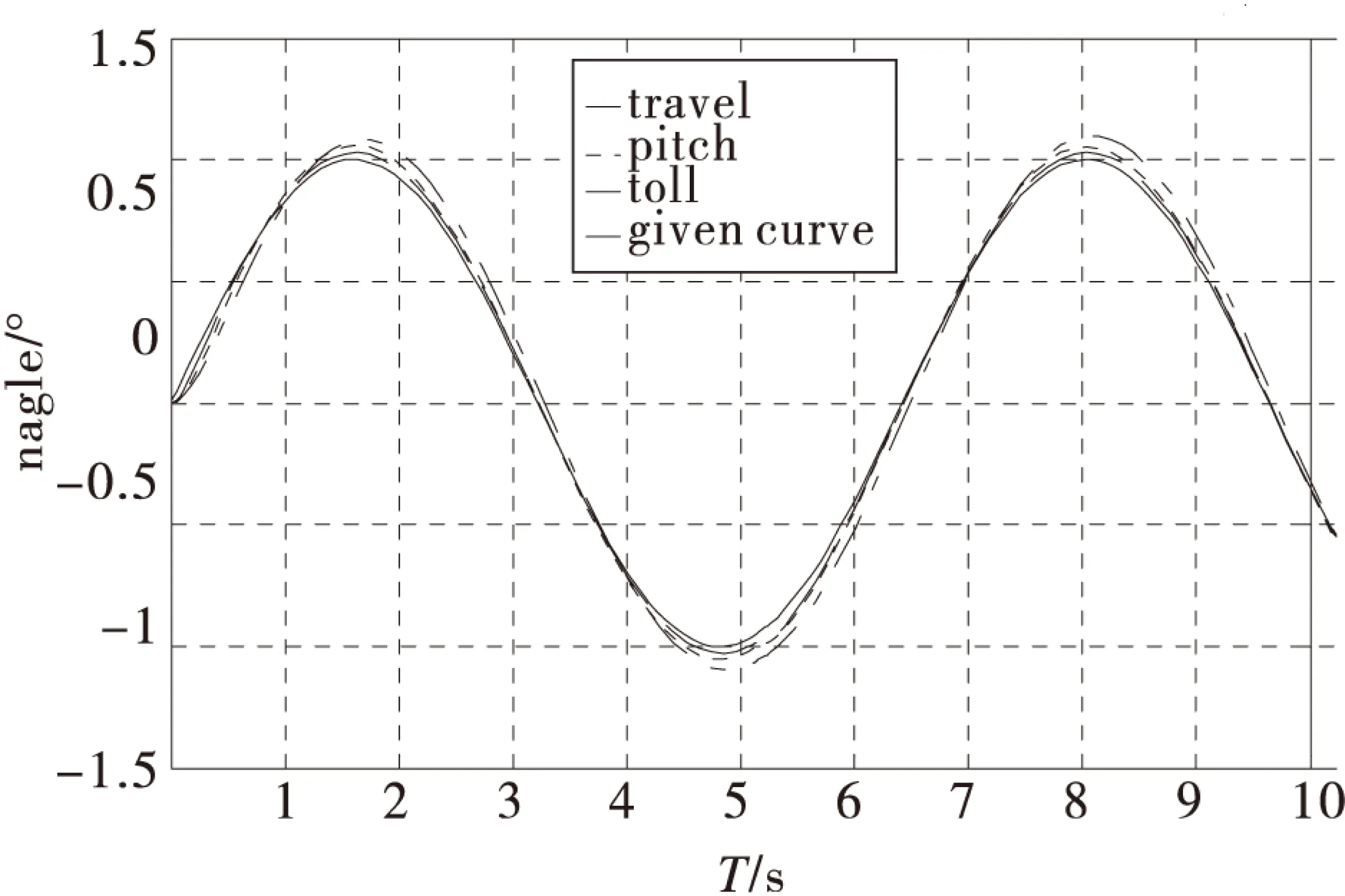
图3 姿态角仿真曲线

在得到良好的仿真结果后，在四旋翼飞行器上进行实际实验，得到控制效果如下：

如图4所示姿态控制曲线，其中，横坐标轴为T/s，纵坐标轴为angle，图中曲线角度从上至下分别为俯仰角θ、横滚角δ、偏航角φ.各个姿态角给定值为0的情况下，系统能在此状态下保持稳定，说明姿态控制效果比较良好，其中有伴随着0.3°左右的轻微抖动。

如图5所示俯仰角跟踪曲线，在等待系统达到稳定平衡状态稳定的时候，在17 s处给俯仰角增加了6°的给定，可以看出俯仰角能在3 s内正确跟踪所设置角度，最后达到比较稳定的状态，但由于各个姿态角的相互影响，在俯仰角跟踪过程中横滚角也有一定的0.2°左右的小角度抖动。

由图6所示干扰性检测曲线，等各个姿态角处于平稳状态后，在15 s对各个姿态角增加了1°左右的干扰量，可以看出系统在经过5 s后能够逐渐趋于稳定，验证了系统鲁棒性。

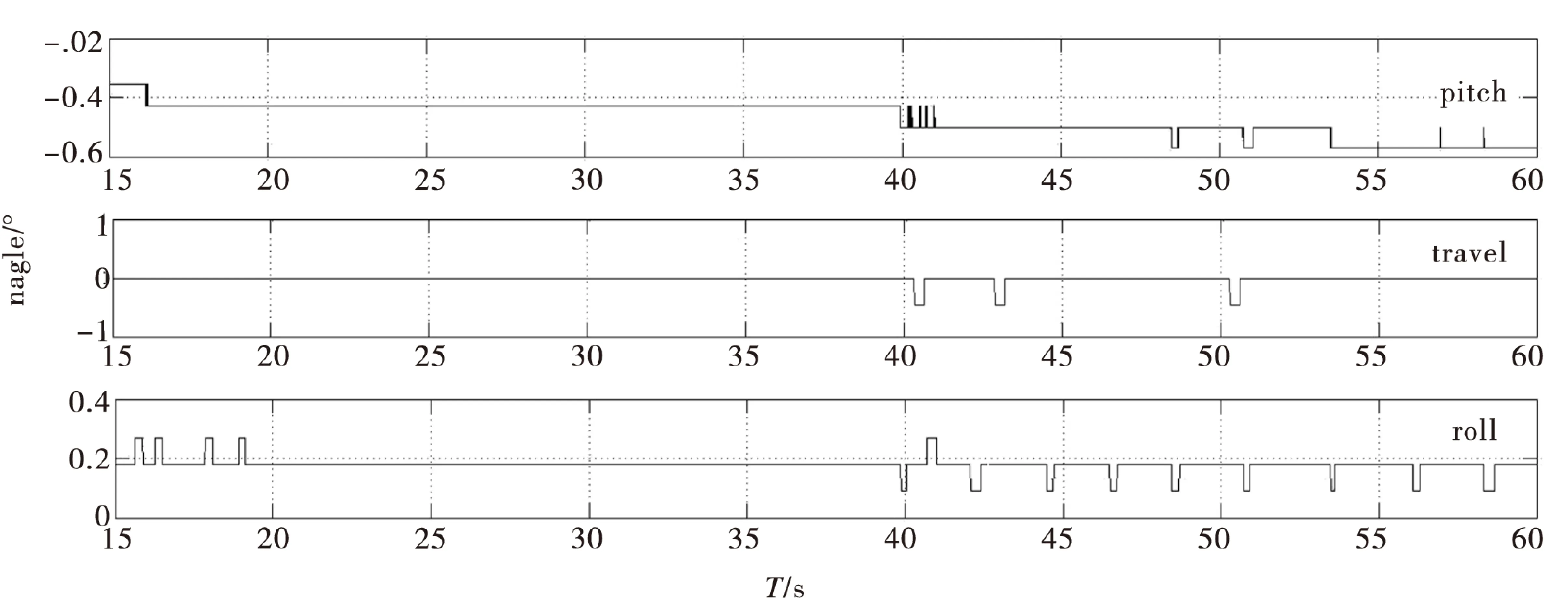
图4 姿态控制曲线

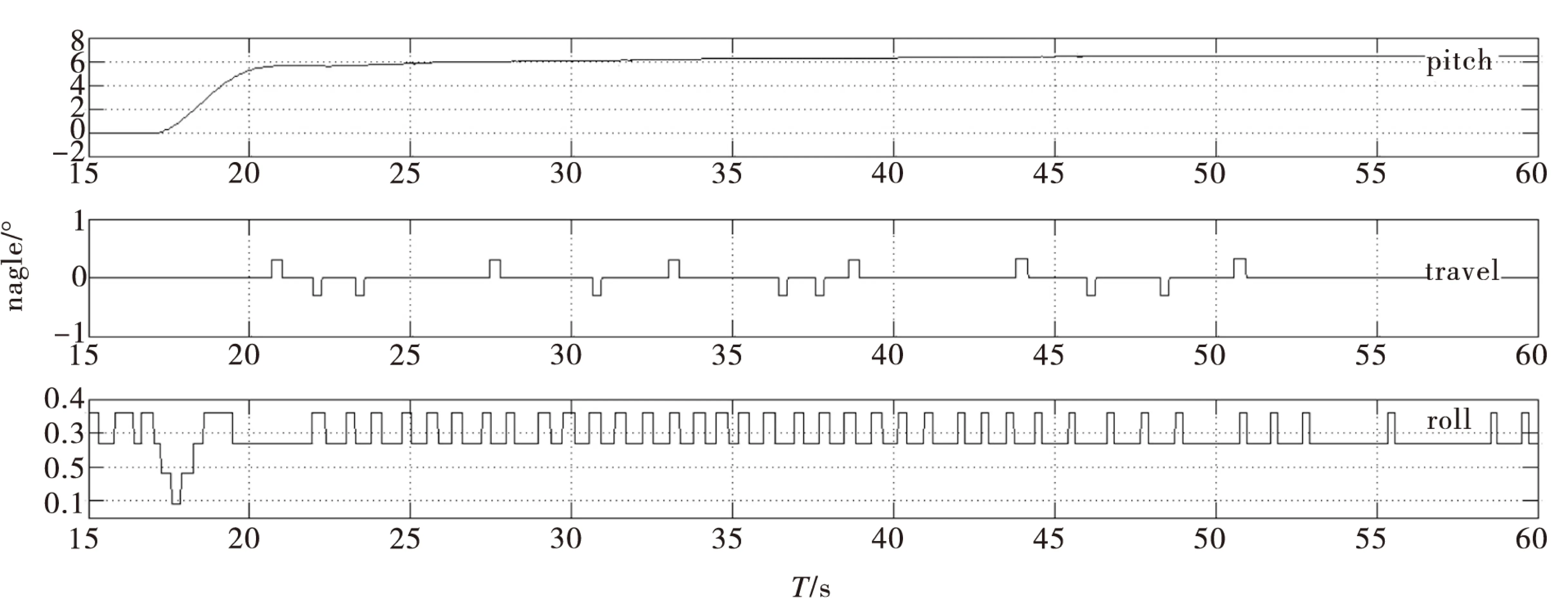
图5 俯仰角跟踪曲线

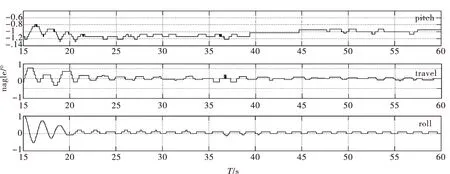
图6 干扰性检测曲线

从上述实测图可知，系统实际性能指标和仿真性能指标有一定的偏差，这是由于电机模型及摩擦力矩误差所造成的死区电压、增量式编码器的采集精度有限以及电机在转动过程中的抖动而造成的稳态误差，是不可避免的。而本文设计的极点配置控制器具有良好的姿态控制效果，在增加一定的干扰情况下，四旋翼飞行器各个姿态角能在一定时间内重新保持稳定，体现了良好的稳定性和鲁棒性。

4 结 语

根据四旋翼飞行器姿态控制系统的数学模型，运用状态反馈极点配置理论设计了四旋翼飞行器姿态控制器。相对于文献提到的自适应逆控制、鲁棒自适应反步控制等控制方法[8-10]，所采用的极点配置控制方法控制器参数简单，动态性能指标设计完善。仿真结果跟实际试验结果都表明，该控制器能良好的控制四旋翼飞行器达到指定姿态，满足四旋翼飞行器姿态控制的稳定性和快速性的要求，并具有较强的鲁棒性。

[1] OLFATI-SABER R. Nonlinear control of underactuated me chanical systems with application to robotics and aerospace vehicles[D].USA：MIT, 2001.

[2] 李劲松,宋立博,颜国正.基于自适应逆控制方法的小型四旋翼无人直升机姿态控制[J].上海交通大学学报,2012 ,46(6):956-961.

[3] 甄红涛,齐晓慧,夏明旗,等.四旋翼无人机鲁棒自适应姿态控制[J].控制工程,2013 ,20(5):915-919.

[4] ERGINER B,ERDINC A.Design and implementation of a hybrid fuzzy logic controller for a quadrotor VTOL vehicle[J].International Journal of Control ,Automation and Systems,2012,10(1)：61-70.

[5] GUIBERME V, MANUEL G, Francisco R. An integral predictive/nonlinear H∞ control structure for a quadrotor helicopter[J].Automatica, 2010,46(1):29-39.

[6] 张建军,黄庆学,马丽楠.基于MATLAB/Simulink的四连杆机构动力学仿真及改进[J]. 太原科技大学学报,2015,36(5)：390-396.

[7] 王正林,王胜开,陈国顺. Matlab/Simulink与控制系统仿真[M].北京：电子工业出版社,2005.

[8] 曹立佳,张胜修,刘毅男,等. 带有自适应参数近似的块控反步控制器设计[J].航空学报,2011,32(12):2259-2267.

[9] 固高公司.固高教学产品 M at lab 实时控制软件使用手册[M].深圳: 固高公司, 2004.

[10] 韩建达,何玉庆,赵新刚.移动机器人系统-建模、估计与控制[M].北京：科学出版社,2011.

Pole Placement Controller Design for Quadrotor Attitude

XIAO Yong, SUN Zhi-yi

(Taiyuan University of Science and Technology, Taiyuan 030024, China)

Quadrotor attitude control system is multivariate, it possesses sensitivity to interference and strong coupling. To attain the stable control of attitude, the dynamic model of quadrotor at balance point was linearized, and the implementation of state feedback pole assignment, which is applied to assign the pole of closed-loop system under the condition that the performance index of both overshoot and time can be satisfied, was presented. Matlab was used to design a pole assignment controller to test the given algorithm and to realize stable control of quadrotor experimental platform. The given algorithm is proved to be effective and stable.

quadrotor， control of attitude， pole placement

2015-12-10

山西省回国留学人员科研资助项目(2014-058)

肖勇(1991-)，男，硕士研究生，主要研究方向为飞行器控制。

1673-2057(2016)05-0354-05

TP29

A

10.3969/j.issn.1673-2057.2016.05.004