模块化多电平换流器子模块均压方法

渠爱霞，韩如成，许敏敏

(太原科技大学 电子信息工程学院，太原 030024)



模块化多电平换流器子模块均压方法

渠爱霞，韩如成，许敏敏

(太原科技大学 电子信息工程学院，太原 030024)

子模块的均压问题是研究模块化多电平换流器(MMC)的关键技术。针对传统子模块电容电压均衡控制存在调制波计算量大的问题，提出一种优化的电容电压均衡控制策略，该策略在传统子模块电容电压均衡控制的基础上，引入2个开关，并设置2个电容电压偏差参考值与实际值进行比较来判断开关的开通与关断。这种方法不仅可以使电容均压计算量减少，而且可以切除故障子模块。最后，在MATLAB/Simulink中搭建MMC的仿真模型，仿真验证该方法的正确性和有效性。

模块化多电平换流器；子模块；电容均压；电容电压偏差参考值

2002 年，德国学者 R.Marquart 和 A.Lesnicar最早提出了模块化多电平换流器(modular multilevel converter，MMC)拓扑结构的概念[1]。与传统的两电平、三电平换流器拓扑结构相比，MMC不仅具有其原有的优点，而且由于其模块化结构，还具有其它的优势[2]。通过改变接入换流器MMC的子模块数量，来快速实现不同功率和电压等级的要求，这种方法不但可以降低开关频率和谐波含量，而且便于实现集成化设计，缩短项目时间，节约成本等优点[3-5]。因为MMC的优势，使得它在有源滤波、电机拖动、无功补偿及高压直流输电等方面具有良好的发展前景[6-7]。

子模块电容电压相等是MMC正常运行的前提条件，所以电容均压为MMC的关键技术。对于MMC的均压问题，文献[8]提出引入双保持因子和能量平衡因子的分组排序，虽然对传统的电压排序法进行改进，但当子模块数量很多时，实现复杂，开关频率仍高。文献[9]采用桥臂总能量和能量均衡的闭环控制方案来实现子模块电容电压的均衡。但该方法对运算能力要求较高。文献[10]采用子模块电容电压平均值控制和子模块电容电压均衡控制方法，但电容电压均衡控制需计算每一个子模块的电容电压的修正量，造成调制波的计算量增加。本文对子模块电容电压均衡控制进行优化，在额定电容电压和实际电容电压相比较之后，加入开关，对其进行判断。设定合适的额定电容电压和实际电容电压之间偏差的参考值，参考值△U1设为需要均衡调节的最小值，参考值△U2设为电容电压允许的最大偏差。当电容电压偏差大于参考值△U2，小于参考值△U2时，进行电容电压均衡控制；当电容电压小于参考值△U1时，则不进行控制。但当电压偏差大于参考值△U2时，切除子模块。这样不仅可以使调制波的计算简单，而且可以迅速去掉故障子模块。最后，通过仿真验证了该方法的正确性和有效性。

1 MMC的拓扑结构和工作原理

1.1 MMC的拓扑结构

模块化多电平换流器的拓扑结构如图1所示，一个换流器有三相组成，每相由2个完全对称的桥臂组成，且每个桥臂是由若干个子模块(sub module，SM)和电感串联而成，电感可以抑制短路电流和桥臂环流，提高系统运行的可靠性。

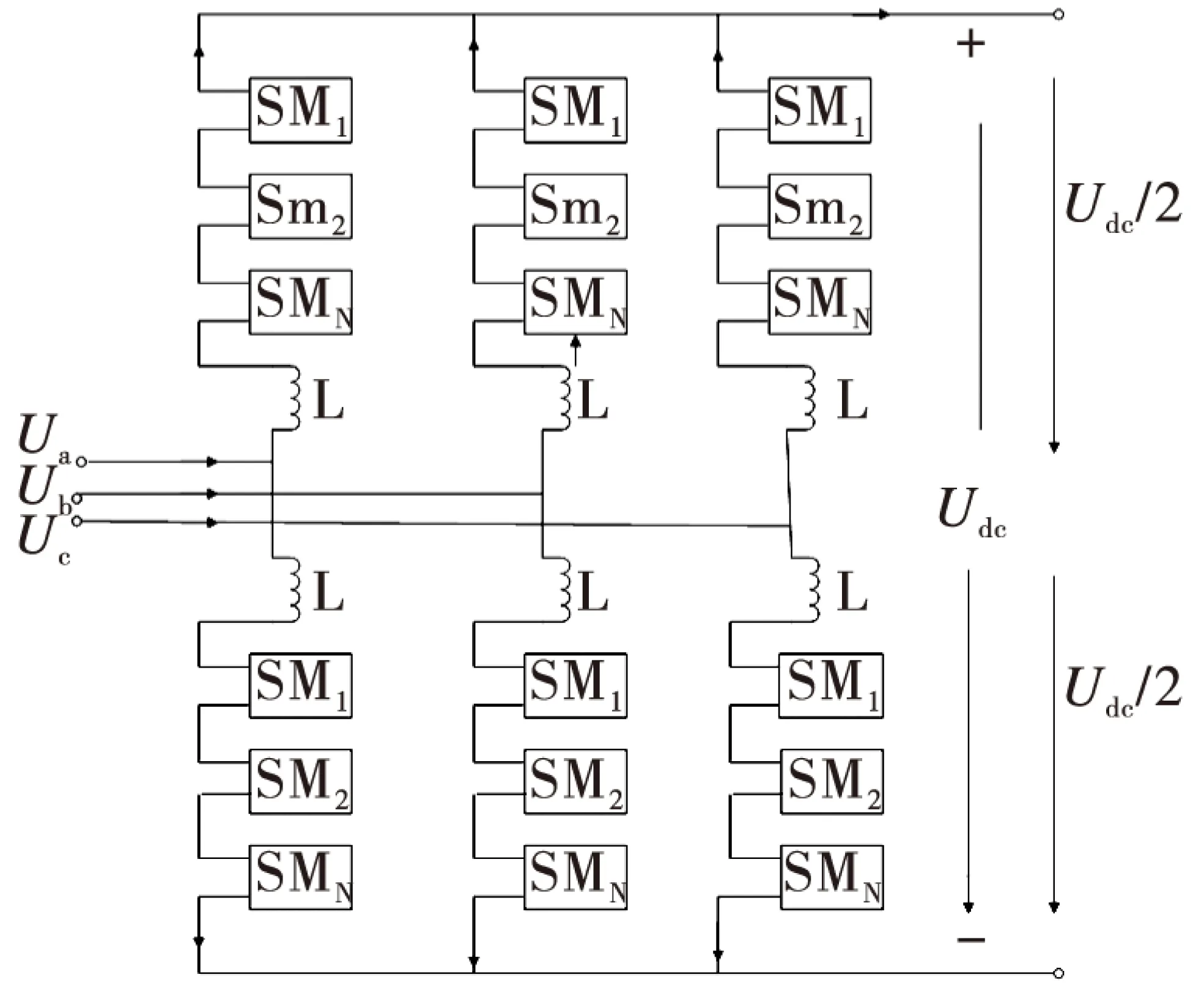
图1 MMC的拓扑结构

图2 子模块的拓扑结构

就目前情况来看，几乎所有的MMC都采用半桥式拓扑结构，如图2所示。子模块的结构是由2个晶闸管IGBT、2个二极管D和1个电容C组成。

1.2 MMC的工作原理

根据IGBT的触发信号和电流方向的不同，其子模块的工作状态也不同，可以分为闭锁、投入、切除。如表1所示。

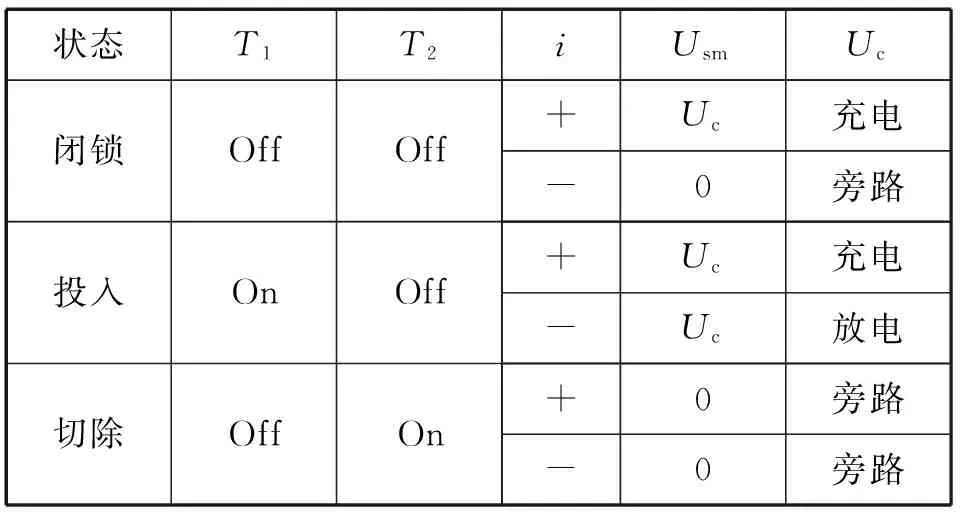
表1 子模块的工作状态

根据表中子模块的工作状态，可以把输出电压等效为一个可控电压源，当T1导通时，输出为Uc；当T2导通时，输出为0.假设MMC一相桥臂内第i个子模块的工作状态函数为Si，并定义如下：

(1)

则第i个子模块的输出电压为:

Ui=SiUc

(2)

MMC的每个桥臂输出电压之和Uarm，为桥臂中串联的所有子模块的输出电压之和。假设桥臂中的所有子模块具有相同的电容电压Uc.

(3)

由于三相MMC具有对称性，以a相为例进行分析，图3为MMC的a相等效电路图。

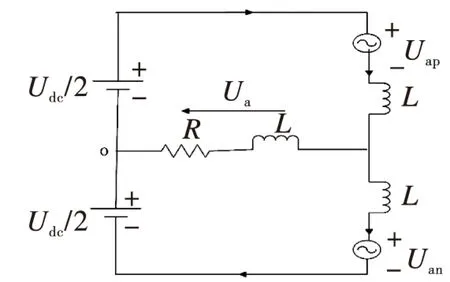
图3 a相等效电路图

由于桥臂上的电感很小，在不考虑桥臂电流在电感上的压降时，可以得:

(4)

则：

(5)

式中:Udc为直流电压，Uap为a相上桥臂电压，Uan为a相下桥臂电压，Ua为a相输出电压。

2 均压方法

模块化多电平换流器MMC的子模块电容相互独立，由于子模块之间开关损耗和触发脉冲的不同，会造成电容电压之间的不平衡。电容电压的不平衡会直接影响换流器的正常运行，进而影响输出电压的波形质量。因此，如何维持电容的均压非常关键。

2.1 传统电容电压均衡控制

传统的均压方法实质是在MMC各子模块调制波的基础上分别叠加子模块电容电压均衡控制和子模块电容电压平均控制的修正量，来保证子模块电容电压的平均分配。

子模块电容电压的均衡控制如图4所示。该控制方法是通过子模块的电容电压与参考电容电压相比较，经过PI控制器后，结合上、下桥臂的电流方向，实现均衡控制。

图4 子模块电容电压均衡控制

因此，以a相桥臂为例进行分析，可知，上、下桥臂子模块的调制波计算公式为：

(6)

式中，Udc为直流侧电压，Ui为交流侧输入电压，UCa为电容电压平均控制的修正量，UjB为电容电压均衡控制的修正量。

2.2 优化电容电压均衡控制

传统均压的方法是在每个子模块原有调制波的基础上进行修正，避免各模块之间因各种损耗和触发脉冲的不同，导致电容电压不相等。可是，由调制波的计算公式(6)可知，当MMC具有很多子模块时，计算每个子模块的调制波显得非常复杂，计算量较大。

因为子模块电容电压是相对一致，而不是完全一致，所以可以对传统子模块电容电压均衡控制进行如图5的改进。优化的电容电压均衡控制是在传统电容电压均衡控制中，设置2个电容电压偏差参考值。

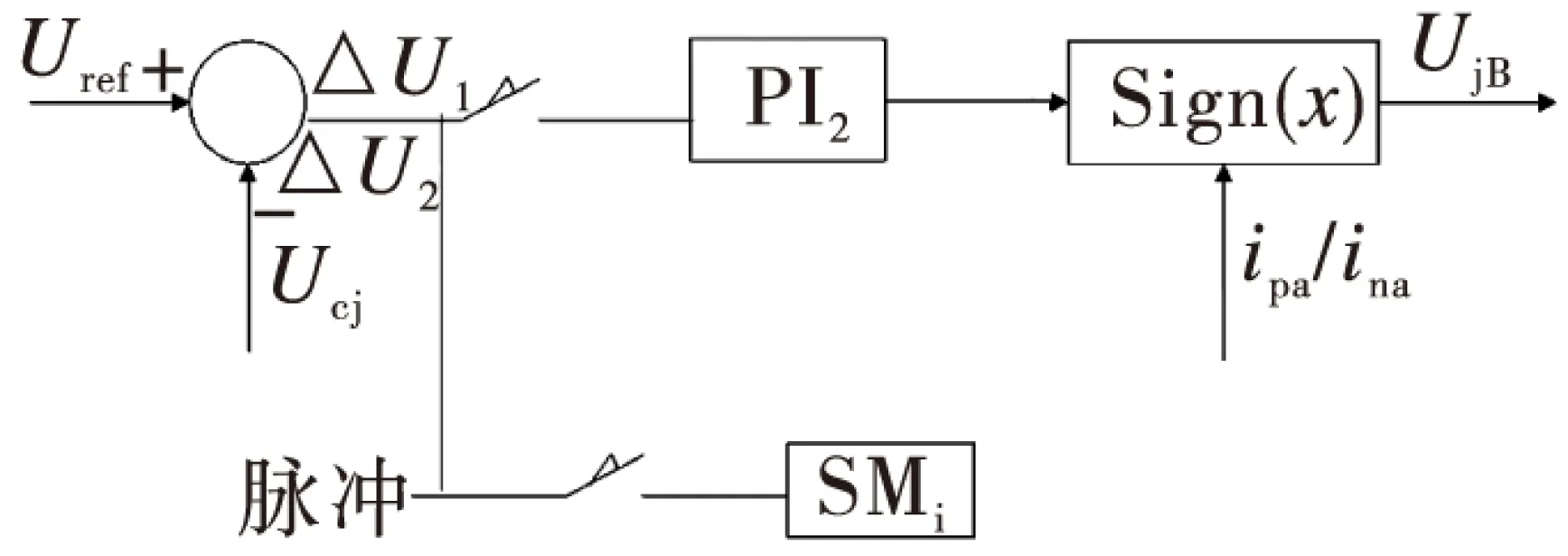
图5 优化子模块电容电压均衡控制

参考值△U1设为需要均衡调节的最小值，当实际电容电压的偏差小于参考值△U1时，不进行电容电压均衡控制时，不影响输出波形的质量；当实际电容电压的偏差大于参考值△U1时，若不进行电容电压均衡控制，会影响输出电压质量，因而必需进行均衡调节。因此，的选取非常重要。△U1选的太小，不能达到最好的优化效果，但△U1选的太大，可能影响模块化多电平换流器的正常运行。

参考值△U2设为电容电压允许的最大偏差，当实际电容电压的偏差小于参考值△U2时，子模块没有损坏，不影响模块化多电平换流器的正常运行；但当实际电容电压的偏差大于参考值△U2时，表明子模块出现故障。因而，△U2的取值也非常重要。

因为参考值△U1是对调制波进行修正，所以，它的选取原则是在不影响调制波产生脉冲的基础上，取最大值，减少计算量。而参考值△U2的设置是为了快速切除故障子模块，它的选取原则是在不影响MMC正常运行的情况下，即根据电容电压的最大偏差选取合适的值。

所以，优化的均压控制方法为：当实际电容电压偏差大于参考值△U1，小于参考值△U2时，开关1闭合，对电容电压进行均衡调整；当实际电容电压偏差小于参考值△U1时，开关1断开，不进行电压均衡调整。当实际电容电压偏差大于参考值△U2时，子模块出现故障，此时开关2断开，子模块切除。这种改进不仅可以简化调制波的计算，使计算量减少，而且可以快速切除故障子模块。

3 仿真结果

为了验证该方法的正确性和有效性，在MATLAB/Simulink仿真中，搭建五电平模块化多电平换流器的仿真模型。仿真的参数选取如下：交流侧电压幅值为5.5 kV，基频为50 Hz，每个桥臂有8个子模块组成，子模块电容参考电压为2 kV，子模块电容为1.9 mF，桥臂电感为2 mH，载波频率是1 kHz，负载电阻为1 kΩ，负载电感为15 mH.

以整流侧a相上桥臂作为研究对象，又因为a相上桥臂四个子模块的一致，所以可以取第一个子模块的电容电压做研究。

参考值△U2的取值是根据最大电容电压偏差进行选取，文中电容电压最大偏差为2.4，所以选取2.4相邻几个值进行分析。因为△U1的取值与△U2有关，所以它的选取是在不影响调制波产生脉冲，并结合△U2的值，根据多次实验结果，选取合适的几组值进行分析。

图6为传统均压输出电容电压的波形，电压在2 kV作用波动；图7～图10分别为△U2=2.3、2.4、2.5、2.6时，△U1取不同值时的电容电压波形。

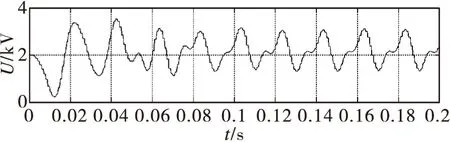
图6 传统均压方法

图7 优化均压方法

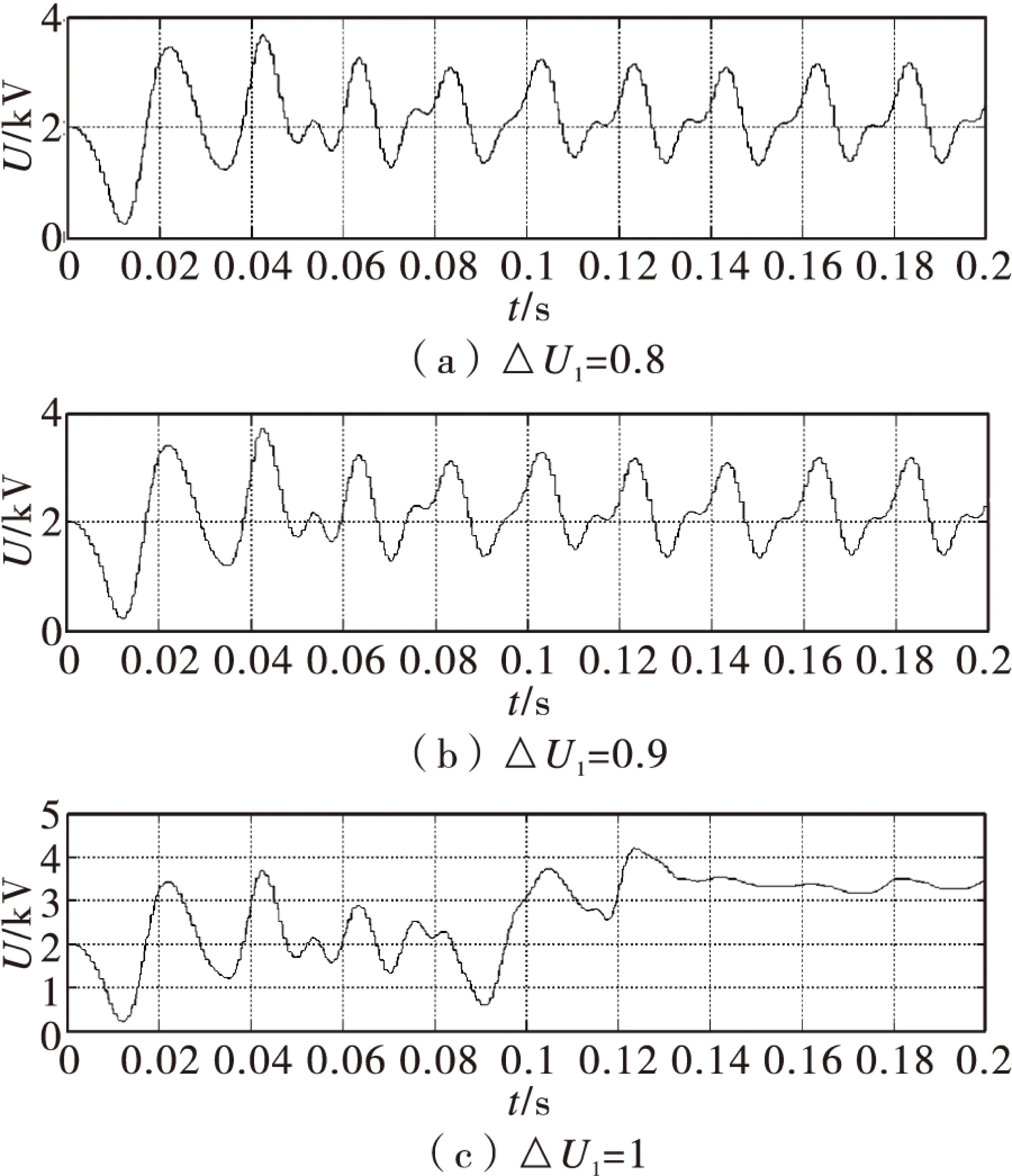
图8 优化均压方法

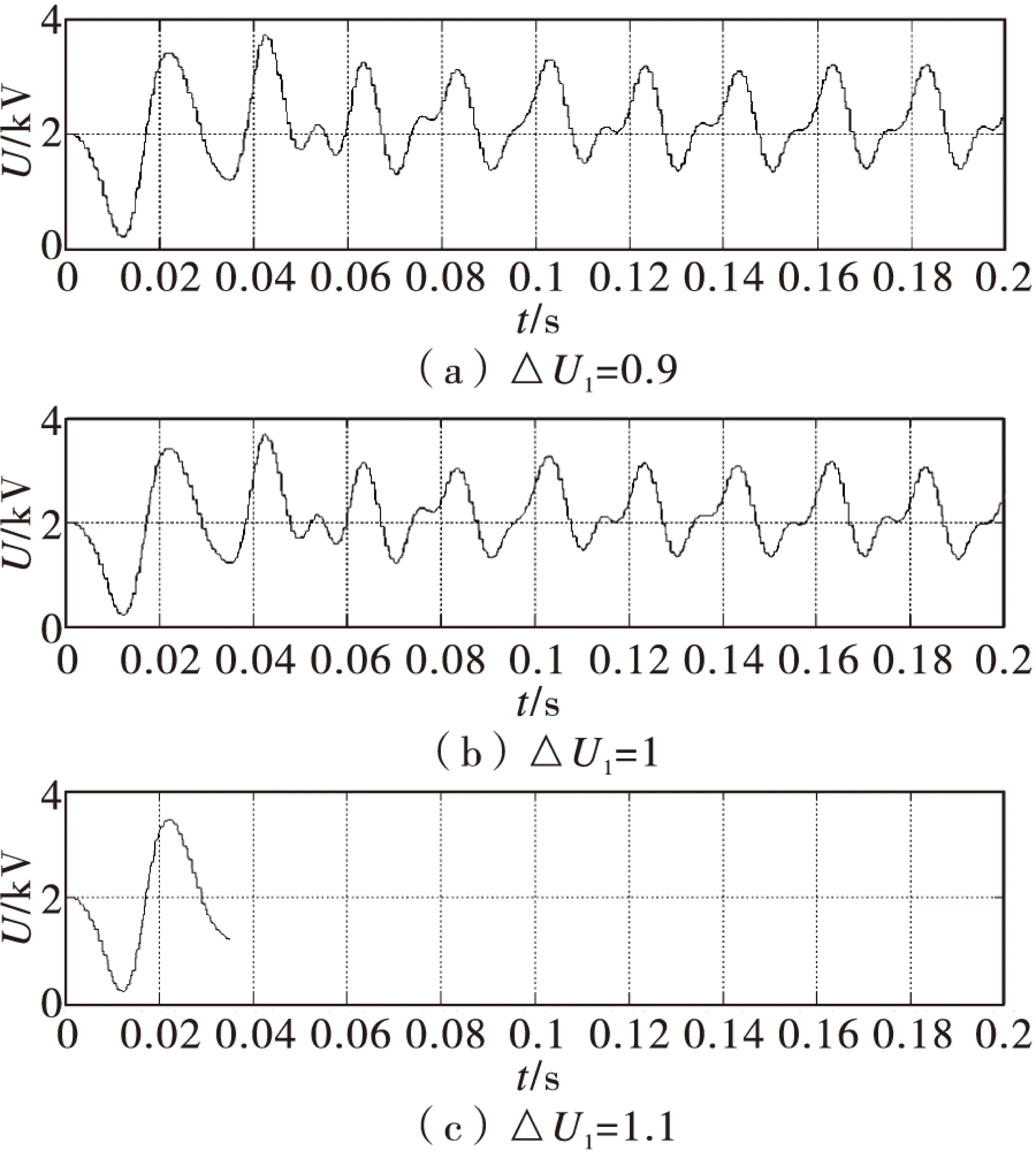
图9 优化均压方法

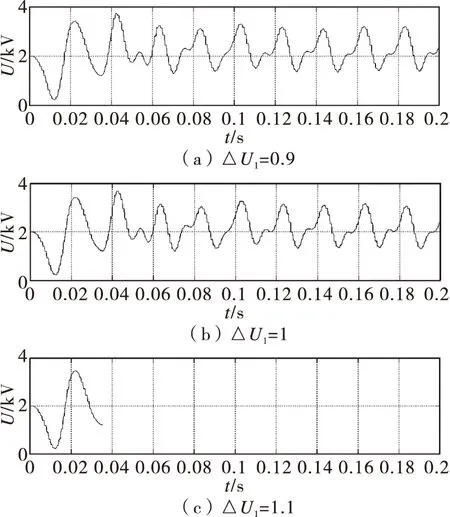
图10 优化均压方法

从图7可以看出，当△U2=2.3时，不论△U1取多少，电容电压的输出波形都是错误的，尤其当△U1=1.1时，MMC运行到0.035时代数循环出现错误，停止运行。这说明当△U2=2.3时，脉冲不能正常输送给IGBT，影响正常运行。

从图8可以看出，当△U2=2.4时，△U1=0.8或0.9时，输出电容电压与图6传统均压输出的波形基本一致，这表明改进的均压方法不影响电容电压的输出质量。但△U1=1时，输出电容电压波形明显变化，因此当△U2=2.4时，△U1=0.9最合适，因为△U1小于0.9时，电容电压输出与传统相同，大于0.9时，电容电压输出与传统明显不同。

从图9可以看出，当△U2=2.5时，△U2=0.9或1时，输出电容电压与图6传统均压输出的波形基本一致，这表明改进的均压方法不影响电容电压的输出质量，但△U1=1.1时，MMC运行到0.035时代数循环出现错误，停止运行。因此当△U2=2.5时，△U1=1最合适，因为△U1小于1时，电容电压输出与传统相同，大于1时，MMC的运行出现问题。

从图9可以看出，当△U2=2.6时，不论△U1取多少，电容电压的输出情况与△U2=2.5时一样。

通过实验可以看出，当△U2≤2.3时，MMC不能正常运行，当△U2≥2.5时，MMC的运行情况与△U2=2.5的基本一致。因为本文的目的是减少调制波的计算量和切除故障子模块，所以△U1取值越大越好，但△U2的取值不易过大。通过上面几组实验的对比可知，当△U1=1，△U2=2.5最为合适。

由调制波的计算式(6)可知，本文所提出的优化均压方法可以在电容电压波动幅值基本一致的情况下，简化调制波的计算量，快速得到所需触发脉冲。最后，由于参考值△U2的引入，可以快速切除故障子模块。

4 结论

本文先介绍模块化多电平换流器的拓扑结构和工作原理，然后针对传统电容电压均衡控制存在计算量大的问题，提出一种优化的MMC电容均压优化方法。通过引入2个开关，并设置2个电容电压偏差参考值与实际值进行比较来判断开关的开通与关断，不仅可以简化调制波的计算量，而且可以快速切除故障子模块。最后，经过多次仿真实验取得合适的偏差参考值，并验证该方法的正确性和有效性。

[1] MARQUARDT R.Modular multilevel converter：An universal concept for HVDC-networks and extended dc bus applications[C]∥2010 International Power Electronics Conference(IPEC)，Sapporo，2010：502-507.

[2] 林周宏，刘崇茹，李海峰，等.模块化多电平换流器的子模块电容电压分层均压控制法[J].电力系统自动化，2015，39(7)：175-181.

[3] SOLAS E，ABAD G，BARRENA J A，et al.Modulation of modular multilevel converter for HVDC application[C]∥2010 14th International Power Electronics and Motion Control Conference (EPE/PEMC 2010).Ohrid，Macedonia：IEEE Japan，2010：84-89.

[4] PEDRAM S，MILLER R D.A new multi-level inverter with FACTS capabilities for wind applications[C]∥Proceedings of IEEE Applied Green Technologie Conference.Denver，America：IEEE，2013：271-276.

[5] 徐政.柔性直流输电系统[M].北京：机械工业出版社，2013：27-30.

[6] GNANARATHNA U N，GOLE A M，JAYASINGHE R P.Efficient modeling of modular multilevel HVDC converters (MMC)on electromagnetic transient simulation programs[J].Power Delivery，IEEE Transaction on，2011，26(1)：316-324.

[7] 喻锋，王西田，林卫星，等.一种快速的模块化多电平换流器电压均衡控制策略[J].中国电机工程学报，2015，35(4)：929-933.

[8] 陆翌.一种模块化多电平换流器的子模块优化均压方法[J].电力系统自动化，2014，38(3)：52-58.

[9] 司志磊，张兴，董文杰.模块化多电平换流器闭环均压策略研究[J].电力电子技术，2012，46(9)：58-60.

[10] 王思蕴.模块化多电平变流器控制方法的研究[D].浙江：浙江大学，2013.

Method for Balancing Sub-module Voltage in Modular Multi-level Converters

QU Ai-xia，HAN Ru-cheng，XU Min-min

(School of Electronic and Information Engineering，Taiyuan University of Science &Technology，Taiyuan 030024，China)

The problem of sub-module′s capacitor voltage balancing is the key technology on modular multilevel converter (MMC).Based on traditional sub-module′s capacitor voltage balancing control of large modulation wave computation problems，a kind of optimized capacitor voltage balancing control strategy was put forward.On the basis of traditional sub-module′s capacitor voltage balancing control，this strategy introduces two switch and sets up two reference values of capacitor voltage deviation compared with actual value to determine the opening of switch on and off.This method can not only reduce amount of calculation for capacitor voltage balancing，but also remove the fault modules.In the end，the MMC simulation model is built in the MATLAB/Simulink，which verifies the correctness and effectiveness of such method.

modular multilevel converter，sub-module，capacitor voltage balancing，the reference value of capacitor voltage deviation

2015-10-15

渠爱霞(1988-)，女，硕士研究生，主要研究方向为电力电子与电力传动。

1673-2057(2016)05-0342-06

TM762

A

10.3969/j.issn.1673-2057.2016.04.002