设置级配碎石功能层的沥青路面有限元模拟
杨大田,李 聪
(国家山区公路工程技术研究中心, 重庆 400067)
设置级配碎石功能层的沥青路面有限元模拟
杨大田,李 聪
(国家山区公路工程技术研究中心, 重庆 400067)
级配碎石功能层指在半刚性基层与沥青面层之间铺筑10~15 cm厚的级配碎石,形成的倒装结构。级配碎石具有典型的非线性力学特性。利用有限元法,建立级配碎石功能层的沥青路面三维有限元模型,通过数值计算,得到沥青面层层底最大拉应力、沥青面层内剪应力以及半刚性基层底部最大拉应力。计算结果表明:级配碎石功能层厚度设计为10~15 cm,回弹模量设置超过300 MPa比较合理。
半刚性基层;级配碎石;功能层;有限元模拟
半刚性基层沥青路面易出现反射裂缝、水损害等缺陷。为了解决上述问题,通常在半刚性基层上铺设土工织物夹层,但该措施存在对环境条件要求高、抗剪切能力弱、成本高等缺点;或通过增加沥青面层厚度,以减少并延缓反射裂缝扩展到沥青层表面。然而这些措施不能从根本上解决反射裂缝的产生[1]。经过多年试验和观察,在欧美等国家,目前逐渐对新建和改建沥青路面采用了柔性基层。柔性基层沥青路面是相对于半刚性基层沥青路面而言的一种路面结构[2]。常见柔性基层包括沥青稳定碎石、级配碎石等。级配碎石铺筑在半刚性基层与沥青面层之间,作为功能过渡层,其处于三向受压状态,从而弥补了级配碎石整体性差的缺点。由于级配碎石不能承受拉应力和拉应变,因此可以消除半刚性基层出现裂缝时释放出来的应变能,抑制沥青面层裂缝产生;同时,级配碎石层增强了路面排水能力,可防止沥青路面水损坏。
在半刚性基层与沥青面层之间加铺级配碎石柔性功能过渡层,在一定程度上弥补了级配碎石柔性基层在整体性方面的不足[3]。本文利用有限元法,建立级配碎石功能层的沥青路面三维有限元模型,通过数值计算得到沥青面层层底最大拉应力、沥青面层内剪应力以及半刚性基层底部最大拉应力,并分析级配碎石功能层厚度及模量对其的影响,为级配碎石功能层厚度设计和配合比设计提供理论依据。
1 路面有限元模型
1.1 几何模型
利用ABAQUS有限元软件建立三维模型,模型尺寸为5 m×5 m×5 m[4]。X轴为行车方向,Y轴为垂直于行车方向,Z轴垂直于X轴和Y轴构成的水平面。几何模型见图1。
图1 几何模型
1.2 模型定义
依次定义材料属性、装配件、分析步、施加荷载和边界条件、划分网格、提交工作、结果可视化。其中定义材料属性和装配件时,根据路面结构实体的分层特点,分层定义材料属性。计算时,模型单元类型选择为8节点6面体非协调模式单元类型,而非协调模式单元适合非线性问题,即适合本文对级配碎石上基层沥青路面结构的分析。
定义边界条件和设置荷载一般初始分析步(Initial)时,荷载可根据具体施加时间在不同的分析步(Step-1,Step-2,……)施加。X方向施加边界条件限制沿X方向的位移为0,即XSYMM(U1=UR2=UR3=0);Y方向施加边界条件限制沿Y方向的位移为0,即YSYMM(U2=UR1=UR3=0);Z方向施加边界条件限制Z方向底面位移为0,即ENCASTRE(U1=U2=U3=UR1=UR2=UR3=0)。荷载采用双圆均布荷载形式,标准轴载F=100 kN,轮胎接地压强P=0.7 MPa,2轮中心间隙d=31.95 cm,荷载半径δ=10.65 cm。根据应力等效原理,把圆形荷载等效转换为矩形荷载,矩形荷载边长为长L=22.77 cm,宽B=15.68 cm[5]。模型网格划分见图2。

图2 网格划分
1.3 材料参数
为分析级配碎石用于沥青路面与半刚性基层间功能过渡层时的受力特点,本文拟定了级配碎石功能层沥青路面结构,并与典型的常规半刚性基层沥青路面结构进行比较分析。级配碎石功能层路面结构与半刚性基层路面结构基本一致,不同之处是将半刚性基层的一部分用10~15 cm级配碎石层[5-7]代替,两者的路面结构参数见表1和表2[8-9]。

表1 路面结构计算参数

表2 材料泊松比
1.4 方案设计
为研究级配碎石模量和厚度对路面各结构层力学性质的影响,拟定了如下3种厚度和5种模量的级配碎石功能层方案:
1) 级配碎石模量定为400 MPa,级配碎石层厚度分别为10、13、15 cm。
2) 级配碎石层厚度定为13 cm,级配碎石模量分别为300、350、400、450、500 MPa。
2 结果及分析
2.1 级配碎石功能层厚度对沥青面层应力的影响
当级配碎石模量为400 MPa时,沥青混凝土层底部处的最大拉应力值随级配碎石功能层厚度的变化规律见图3。
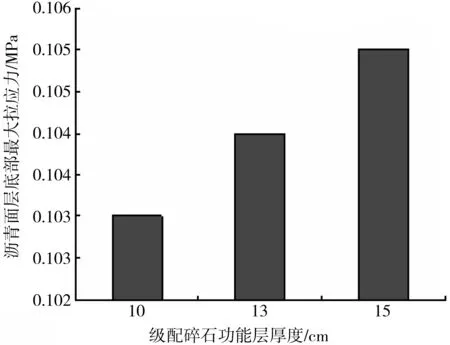
图3 沥青面层层底最大拉应力与级配碎石功能层厚度关系
从图3可知,级配碎石功能层的厚度从10 cm增至15 cm时,沥青面层底部处的最大应力值增长率为1.0%,表明级配碎石功能层的厚度对沥青混凝土层底部最大拉应力的影响较小。
当级配碎石模量为400 MPa时,沥青混凝土层不同深度处随级配碎石过渡层厚度变化的最大剪应力值见表3。
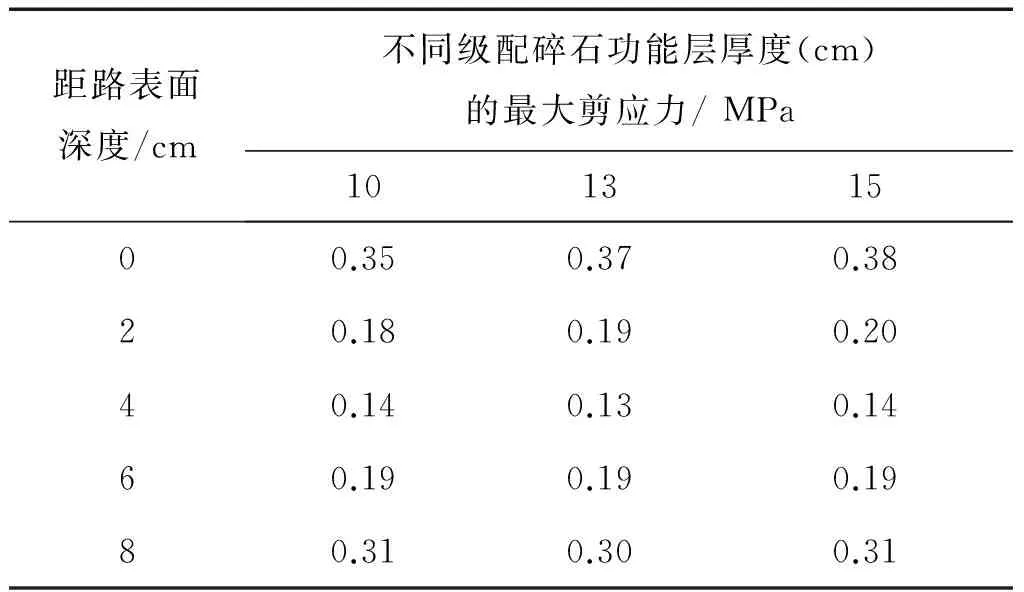
表3 沥青混凝土层不同深度处最大剪应力
从表3可以看出,随着级配碎石功能层厚度的变化,沥青混凝土层底部的最大剪应力几乎没有变化。由此可知,级配碎石功能层厚度在10~15 cm较为合适。
2.2 级配碎石模量对沥青面层应力的影响
本文对相同厚度级配碎石层和半刚性基层(厚度为13 cm)沥青混凝土路面进行了计算,结果见表4。

表4 沥青面层底部X方向的最大应力
注:半刚性基层模量取1 500 MPa。
从表4可以看出,在半刚性基层与沥青面层之间未加级配碎石功能层时,沥青面层底部X方向最大应力值为-0.222 MPa,比加了一定厚度级配碎石功能层的沥青面层底部的应力值要大。在设置了相同厚度的级配碎石功能层沥青路面结构中,级配碎石模量越大,沥青面层层底最大应力值就越大,且为拉应力。
由于级配碎石功能层处于半刚性基层与沥青面层之间,因此,级配碎石层表面受到拉应力,但由于级配碎石具有不传递拉应力的良好特性,故致使面层的拉应力不能传递到半刚性基层上,从而具有很好的消除拉应力功能。沥青面层底部最大拉应力值增长较小,模量从300 MPa增至500 MPa时,沥青面层层底的最大拉应力从2.265倍降至1.982倍,表明级配碎石模量对沥青面层层底的应力具有较大影响。
由于沥青面层发生剪切变形与其受到剪应力有关,因此本文还分析了沥青面层不同深度处的剪应力值,见表5。
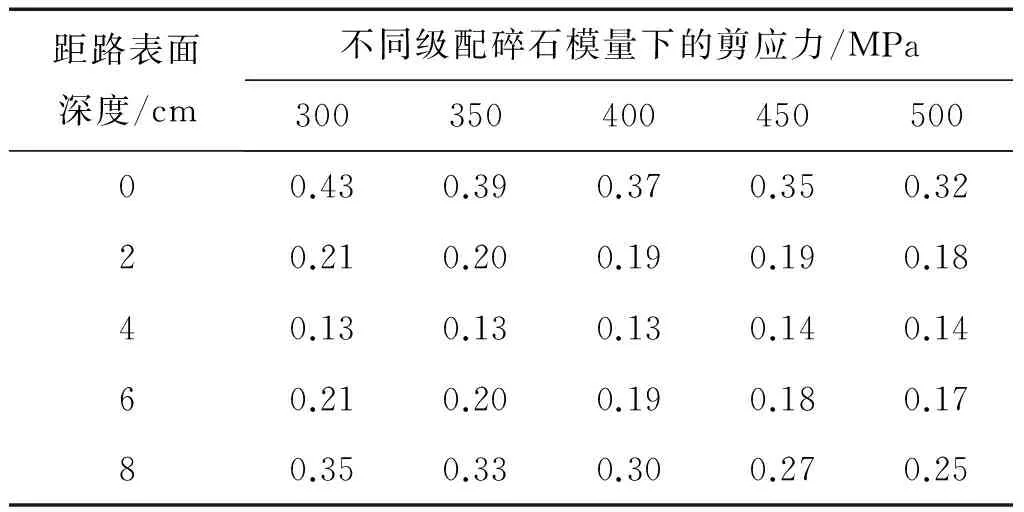
表5 沥青面层不同深度处的剪应力
由表5可知,沥青面层与级配碎石结合处的剪应力相对较大,同时沥青面层顶部的剪应力也较中间部位的大,具有沥青面层顶部和底部剪应力大的特点,这与一般典型半刚性基层沥青路面剪应力变化规律不一致[10]。且随着级配碎石模量的增大,在面层和级配碎石与沥青面层结合处的剪应力明显减小,表明级配碎石模量对沥青面层内的剪应力有明显影响。
3 结论和建议
1) 级配碎石功能过渡层的厚度对沥青面层层底受力、面层内部剪应力和最大应力有一定影响,但影响较小。基于有限元计算比较和分析,并考虑经济技术等综合因素,建议级配碎石层厚度为13 cm。
2) 级配碎石模量对沥青路面面层层底应力和沥青面层内的剪应力有显著影响。进行级配碎石配合比设计时,级配碎石模量应不小于300 MPa。
[1] 宋志峰,刘海鹏,蒋应军.级配碎石基层沥青路面非线性力学响应分析[J].交通标准化,2014,42(11):51-54.
[2] 李福普,严二虎.沥青稳定碎石与级配碎石结构设计与施工技术应用指南[M].北京:人民交通出版社,2009.
[3] 王 亮.级配碎石上基层路用性能研究及路面结构分析[D].沈阳:沈阳建筑大学,2011.
[4] 谢 晖.基于FWD检测的半刚性基层沥青路面结构性能评价[D].上海:同济大学,2007.
[5] 从志敏,邹晓翎,龚红仁.重载对沥青路面车辙及疲劳寿命的影响[J].武汉理工大学学报,2013,35(4):54-58.
[6] 交通部中交公路规划设计院.公路沥青路面设计规范:JTG D50—2006[S].北京:人民交通出版社,2006.
[7] 曲立杰,张德才.沥青路面级配碎石层应力消散的细观研究[J].公路交通科技,2014,31(9):13-17.
[8] 张敏江,王 亮,周 宇.级配碎石上基层沥青路面结构力学响应分析[J].沈阳建筑大学学报(自然科学版),2011,27(1):64-69.
[9] 任成志.沥青路面当量回弹模量的研究[J].中外公路,2003,23(6):23-24.
[10]夏文军,杨大田.半刚性基层沥青路面剪应力正交分析[J].西部交通科技,2009(7):28-31.
Finite Element Simulation of Asphalt Pavement with Graded Debris Layer
YANG Datian, LI Cong
Graded debris function layer indicates laying 10~15 cm thick graded debris between half rigid bed course and asphalt pavement, which forms a inverted structure. Graded debris has typical non-linear mechanical properties. This paper introduces using finite element method to set up 3D finite element model for asphalt pavement with graded debris function layer, with numerical calculation, we obtain max. tensile stress at the bottom of asphalt pavement, inner shearing force of the asphalt pavement and max. tensile stress at the bottom of the semi-rigid bed course. Results of calculation show: It is suitable to design 10~15 cm thick graded debris function layer and the 10~15 cm, and the modulus of resilience be over 300 MPa.
Semi-rigid bed course; graded debris; function layer; finite element simulation
10.13607/j.cnki.gljt.2016.05.001
国家山区公路工程技术研究中心开放基金(gsgzj-2012-12)
2016-07-05
杨大田(1973-),男,重庆市人,博士,讲师。
1009-6477(2016)05-0001-04
U416.217
A

