基于核主成分分析的二次雷达脉冲信号初始特征提取*

杨 卓，李大超

基于核主成分分析的二次雷达脉冲信号初始特征提取*

杨 卓**1，李大超2

（1.中国电子科技集团公司第三十六研究所，浙江嘉兴314033；
2.海军驻上海地区电子设备军代室，上海201800）

针对二次雷达脉冲信号的特征选择与分类问题进行研究，提出了一种基于核主成分分析（KPCA）的初始特征提取方法。根据二次雷达脉冲信号的特点，首先经过数据整编、预处理，获取样本的初始特征参数；然后利用KPCA方法对特征参数进行主成分组合，以消除信号特征间的相关性和压缩特征向量的维数，最后利用聚类工具进行分类。数学分析和可视化实验结果都表明这种分析方法是有效的。试验还表明，KPCA在特征选取方面性能优于PCA。

二次雷达信号；脉冲信号；特征提取；核主成分分析；主成分分析

1 引 言

作为传统雷达的补充，二次雷达最初是为了在空战中分辨出敌我属性而发展的，应答方通过固定的脉冲编码格式来回报敌我属性。随着时代的发展，二次雷达在军用和民用航空管制（Air Traffic Control，ATC）领域得到越广泛的应用，多种调制、编码方式、加密协议也开始应用于二次雷达。不局限于目标识别，应答方甚至可以按规定的格式回报地址码、飞行高度、速度、航向等信息，和通信、数据链的界限越来越重叠。

对于侦察方来说，从情报效益来看，二次雷达虽然属于非合作信号，其往往采用几个固定频点传输，截获相对容易，携带的信息具有较高的情报价值。从情报分析难度来看，北约体制二次雷达应用最广泛，主要分为1、2、3/A、4、C、S等6种模式，其传输规则和协议已经研究得比较透彻。但其他国家也在有针对性地发展自己的二次雷达，出于保密原因，其信息传输协议可能随时间发生变化。实际环境中，在某一空域某一时间段内，有可能目标较多，导致同频脉冲密度较高。不了解询问应答双方规则的前提下，人工进行信号分析判决需要耗费较大精力。

目前已经有不少文献针对脉冲信号自动分类识别展开了研究。文献[1]通过瞬时自相关提取脉冲信号的瞬时频率特征，在此基础上进行级联归一化处理，从而得到能表征脉冲信号调制特性的统计分类特征向量并实现了自动分类，获得了较好的分类正确率。文献[2-3]利用模糊聚类算法对脉冲信号进行分选，通过自适应确立聚类中心和聚类半径，改善分选流程的同时，提高了分选正确率。文献[4-5]利用神经网络对脉冲信号进行分选，其中，文献[4]将粒子群算法和神经网络有机结合，文献[5]则采用了自组织特征映射神经网络算法，通过不断训练迭代，提高了类内聚敛性和类间离散性。文献[6]针对雷达信号，利用特征提取算法得到特征向量，然后应用支持向量机（SuPPort Vector Machine，SVM）分类器对特征值进行识别，取得了较好的识别效果。

上述文献主要对未知雷达脉冲信号进行分类、分选，可以自组织、无监督地发现雷达辐射源在多维特征参数空间中的分布特征，从而对目标进行分类，但主要缺点在于计算量和复杂度较大。相比未知雷达信号而言，二次雷达具有其固有特征，如脉冲包络形状、脉冲宽度和脉冲间隔周期具有一定规律，且一般存在框架脉冲，作为信息传输的先导。

针对二次雷达脉冲信号的特性，本文基于模式识别的分析框架，在特征处理环节应用了核主成分分析法（Kernel PrinciPal ComPonent AnalYsis，KPCA）提取到多组规则脉冲串，得到了一些有意义的分析结果，可以作为后续协议分析的支撑。

2 基本原理

根据实际操作经验，对于未知协议二次雷达脉冲信号的分析识别，从模式识别的角度可以分为4个步骤，如图1所示。

图1 基于模式识别的脉冲信号分析流程Fig.1 The Process of Pulse signal analYsis based on Pattern recognition method

下面依次对每个阶段的工作内容和步骤进行简要介绍。

第一步 数据整编：该阶段的主要目的是对原始脉冲信号的参数化输出进行规范，按固定格式整编后的脉冲描述字（Pulse DescriPtion Word，PDW）样本是下一阶段分析识别的基础。

第二步 样本初步处理：该阶段的主要目的是对整编数据进行预处理，去噪、去偏移、筛选后得到初始特征。预处理的方式依赖于数据的类型和来源，典型方法包括中心化变换、归一化处理、正规化处理、标准化处理、Q检验法、特征筛选处理等。在实际操作中，根据样本的方差、量纲差异等因素，可以灵活选用相应的方法。通过样本初步处理，实现了从数据空间向特征空间的转换。

第三步 特征处理：对于多特征的数据来说，很难用图形直观地表示所有特征的变化情况。特征处理的核心思路是空间维数压缩，通过映射或变换的方式获取最有效的特征，实现维数降维后，利用统计或图形工具进行直观分析，进而可以得到数据规律并实现分类。特征处理主要包括特征选择和特征提取两类方式，特征选择是从原始特征中挑选出最直观的特征，以达到降维的目的；特征提取则是通过线性或非线性变换，将原始特征降维，得到二次特征。

第四步 类型识别：经过特征处理后，特征仍不直观的数据可以采取各种分类、聚类算法进行类型识别，也可以借助操作者的经验进行辅助判别。以聚类分析为例，通常是在先验知识不足的情况下，利用数学统计方法分析特征向量间的距离及离散程度，按照特征间的距离划分类别，从而实现特征空间向类别空间的转换。

在实际操作过程中，上述4个过程并不一定会依次遍历。举例来说，某样本如果经历了数据整编、样本初步处理、特征处理3个过程后，特征非常明显，经可视化显示后，操作员可直接分类，不进入第4个步骤。

其次，特征处理、模式识别的方法较多，参数设置不同也会带来较大差异，目前还不存在一种通用的理论可以遵循。在实际操作时，根据样本统计特点，可能要不断迭代、寻优，针对实际样本寻找相对“适用”的处理方式。

3 实验分析

本节结合实采二次雷达脉冲数据进行分析，目的是提取应答信号同步头框架脉冲。

3.1 数据整编

对某一时段接收的疑似二次雷达脉冲信号进行整编处理，共计数万个样本，脉冲描述字主要包括幅度、脉宽、频率、脉冲到达时间、脉相等变量。根据先验知识，同个目标的信号幅度一般不会有太大突变；脉宽经过直方图统计，绝大多数保持稳定的值，经过分析员初判脉内波形，不太可能采用脉内相位调制，也不进行考虑。经过初步筛选，样本可能采用频率、脉位混合编码，故主要对上述两类变量进行分析。

3.2 样本初步处理

根据二次雷达应答信号的规则，即一般带有同步头脉冲（或者称框架脉冲）且结构固定、同步头脉冲的时间间隔具有一定规律（方差不会太大），首先，制定匹配模板，从原始脉冲描述字中筛选出一组样本，每个样本赋予9个原始特征值，分别是起始5个脉冲的频率值f1、f2、f3、f4、f5以及相应的脉冲间隔t1、t2、t3、t4；其次，进行去噪处理，基于脉冲间隔的方差、偏离度，删除样本中的噪声（奇异点）；最后，进行标准化处理，这种方法可将量纲不一（频率和时间的单位不同）、范围不同的各列特征值转化为均值为0、标准差为1的数据。经过样本初步处理，得到初始特征，可以进行后续的特征处理。

3.3 特征提取

主成分分析（PrinciPal ComPonent AnalYsis，PCA）是一种广泛应用的特征提取方法，基本思想是将特征空间从n维映射到W维正交空间，具体计算方法参见文献[7]。经PCA转换后，其新特征（又称为主成分）是线性无关的，信息量通过“方差贡献率”（又称为解释方差）（Variance ExPlained）来评估。根据文献[8]，前3个主成分的解释方差累计贡献率应达80%以上为宜。这样一来，通过对比有限几个主成分的分布规律，就可以对数据进行融合归类，并去除掉奇异样本。

对初始特征进行PCA处理。特征空间内前两个主成分的投影以二维平面图绘出，如图2（a）所示。特征空间内各主成分的方差贡献率以帕累托图的形式表示，如图2（b）所示。可以观察到，PCA的降维效果并不理想，前3个主成分的方差累计贡献率不到50%，假如提取前3个主元进行归类，则浪费掉大量原始信息，有可能导致后续的分析失真严重。这种现象是由于PCA的线性映射降维局限性造成的，抽取的特征并不一定是最优解。本文采用核主成分分析方法，其基本理论是将低维空间线性不可分的样本通过非线性映射到高维特征空间，然后使用PCA提取主成分，从而进行降维。

图2 PCA特征提取结果Fig.2 The feature extraction results based on PCA

对于输入空间的M个样本xk（k＝1，2，…，M），xk∈RN，确保其正规化，变换为特征空间中的样本点Φ（x1），Φ（x2），…，Φ（xM）。假设特征空间中的样本点符合正规化条件，其构成的协方差矩阵为

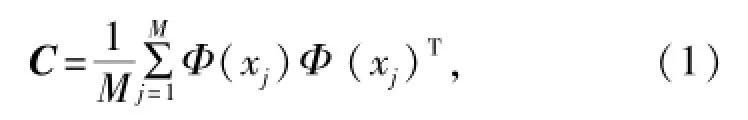
因此，特征空间中的PCA是求解方程

式中：λ代表特征值；v代表特征向量。注意到v可由Φ（xi）（i＝1，2，…，M）线性表示：

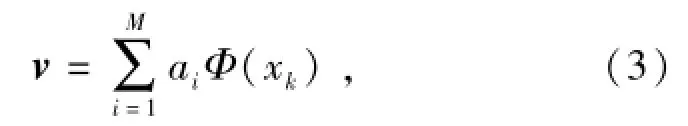
将式（3）代入式（2），并在等式两端对Φ（xk）作内积，得到

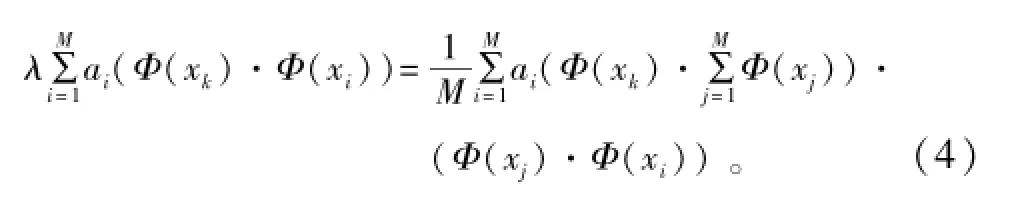
通常非线性变换函数Φ（）非常复杂，核方法则通过向量的内积变换绕过了映射函数Φ（）。通过构造一个核函数，实现如下变换：

将式（5）中的K（xi，xj）代入式（4），并进行简化，得到

式中：K是由K（xi，xj）构成的方阵，通过求解式（6），即可获得特征值λ和特征向量α，进而得到样本在特征空间的投影γW，见式（7）：

式中：W由特征值λ的个数决定。

值得注意的是，在进行内积变换时，核函数必须满足Mercer条件[9]。通常应用较广的是高斯径向基函数[10]（Radial Basis Function，RBF），其形式如下：

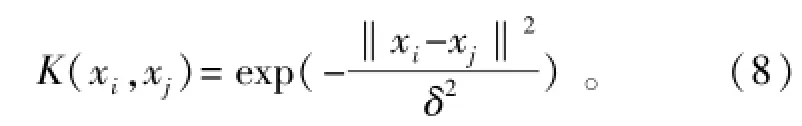
式中：δ是函数的宽度参数，需根据样本的分散情况灵活设置。根据文献[11-12]，若δ→0，则测试样本点容易出现“过分类”的现象，推广能力较差；若δ→∞，则对测试样本一视同仁，正确判别能力为零（把所有样本均判为同一类）。在确定高斯径向基函数的宽度δ时，比较典型的方法有梯度下降法[13]、交叉验证法[14]和网格法等。本文采用网格法，搜索到最优δ＝2。将该值代入高斯径向基函数，进行KPCA处理。如图3（a）所示，特征空间内前两个主成分的投影以二维平面图绘出；特征空间内各主成分的方差贡献率以帕累托图的形式表示，如图3（b）所示。

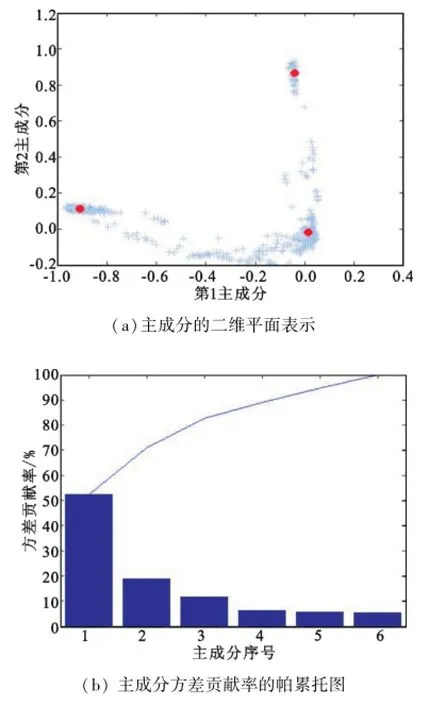
图3 KPCA特征提取结果Fig.3 The feature extraction results based on KPCA

不同参数下，KPCA和PCA的性能对比见表1，可见采用PCA法，前3个特征的方差贡献率仅为50.9%；采用KPCA法，在最优宽度参数条件下（δ＝2），前3个特征的方差贡献率达到82.8%，优于PCA法。

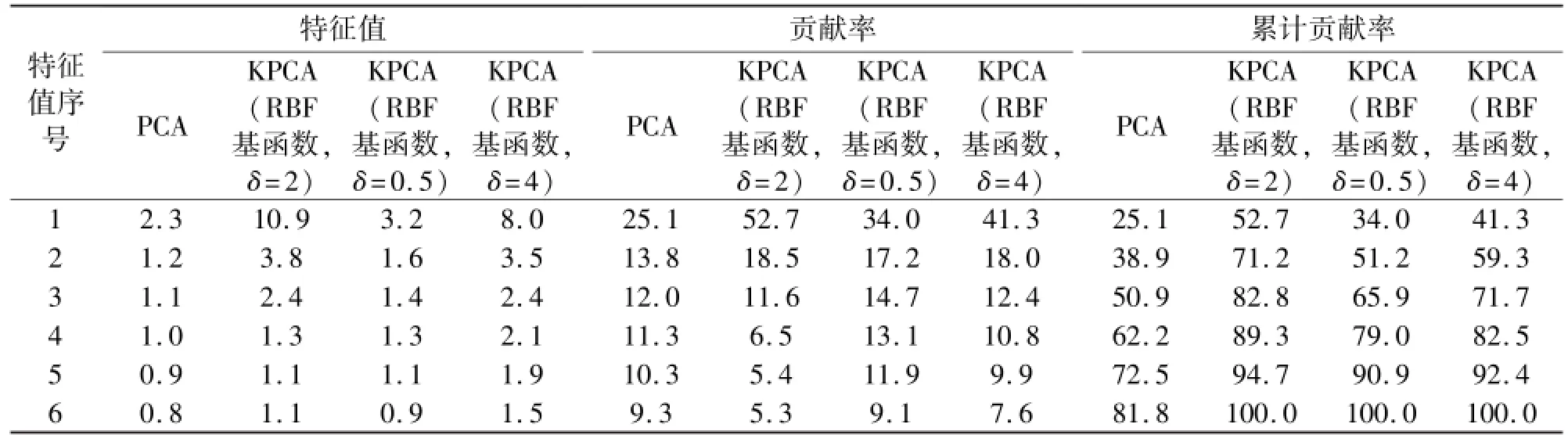
表1 PCA与KPCA性能比较Tab.1 Performance comParison betWeen PCA and KPCA

3.4 类型识别

样本经KPCA运算，选取合适的基函数和宽度参数，主成分的方差贡献率大大提升，更加易于归类。值得注意的是，样本在经过初步筛选后，仍不可避免的混有野点。野点样本会对KPCA的主元产生影响，从图3（a）来看，部分特征样本产生交叠。

基于模糊聚类工具，我们对主成分的聚类中心点进行了提取（如图3（a）中红点所示），其对应的前3个主成分值见表2。为确保分类正确率，我们采用基于欧式距离的检测方式，将范围外的样本剔除，得到的分类结果见图4。

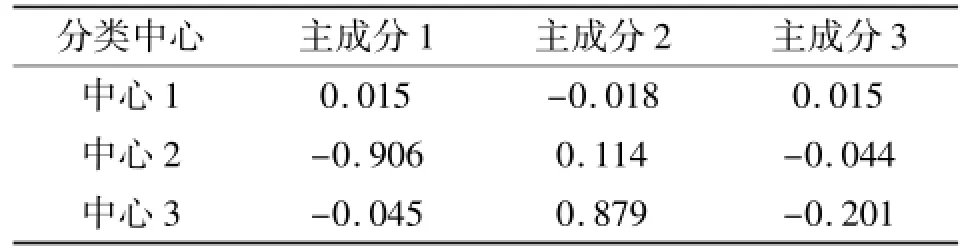
表2 特征空间内的分类中心Tab.2 Central classification results based on feature sPace

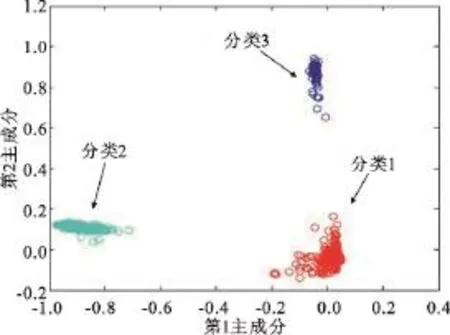
图4 基于KPCA的分类结果Fig.4 Classification results based on KPCA

相比较而言，对图2（a）所示的PCA主分量进行聚类，由于数据在特征空间的分布效果不理想，如聚类半径设置过小，则容易识别出多个重复模式；如聚类半径设置较大，又容易产生类间模糊，如图5所示。将KPCA特征空间的主成分映射回数据空间进行平均处理，最后得到3组较规则的脉冲串结果，如表3所示。3组模式的频率参量均遵循同样的规律，具有明显的框架脉冲的特征。PCA则得到两组分类结果，相比KPCA少了一组结果，且第4个脉冲间隔也有一定模糊。

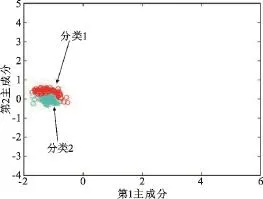
图5 基于PCA的分类结果Fig.5 Classification results based on PCA

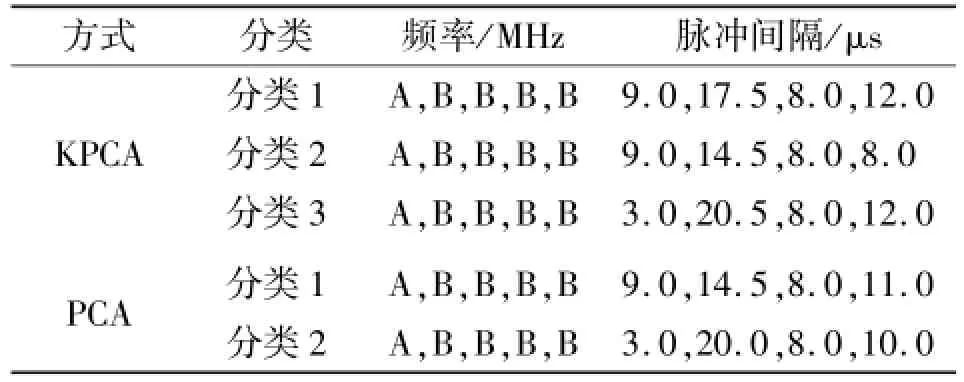
表3 框架脉冲分析结果Tab.3 AnalYsis results of Pulse brackets characters

4 结束语

本文将模式识别技术初步应用于二次雷达脉冲信号分析，对实际环境中采取的脉冲描述字采取如下处理步骤：

（1）基于先验信息，采用9个原始参量f1、f2、f3、f4、f5、t1、t2、t3、t4构造样本；

（2）基于脉冲间隔的方差、偏离度，删除样本中的噪声（奇异点）；

（3）对样本进行标准化处理；

（4）采用RBF基函数，构造K矩阵，搜索合适的宽度参数，采用KPCA算法将样本映射到特征空间；

（5）在特征空间采用合适的聚类半径对主成分进行分类。

试验结果表明，这种方法对于工程具有一定实用意义：

（1）基于KPCA的模式识别方法，降维的同时又尽可能多的反映原始信息，类内聚敛性和类间离散性优于PCA法；

（2）聚类得到的结果做为筛选规则，可以支撑对海量样本数据的进一步处理，有利于后续的信号协议分析工作；

（3）本文的推导方法基于框架脉冲的先验知识，在实际应用中并不一定总能得到正确的先验知识，未来计划针对二次雷达信号在不确定情况下的分选识别进行更深入的研究；

（4）试验中，发现方法还有改进的空间，初始样本如包含过多野点，则可能会对KPCA的稳健性产生影响，需要采用改进的鲁棒KPCA算法对野点样本进行剔除。

[1] 普运伟，金炜东，胡来招.基于瞬时频率二次特征提取的辐射源信号分类[J].西南交通大学学报，2007，42（3）：373-379. PU YunWei，JIN Weidong，HU Laizhao.Automatic classi_ fication of radar emitter signals based on cascade featureextractions[J].Journal of SouthWest Jiaotong UniversitY，2007，42（3）：373-379.（in Chinese）

[2] 张中山，贾可新.粒子群优化模糊聚类在信号分选中的应用[J].舰船电子对抗，2013，36（3）：85-87. ZHANG Zhongshan，JIA Kexin.APPlication of PSO-FCM to signal sorting[J].ShiPboard Electronic Countermeas_ ure，2013，36（3）：85-87.（in Chinese）

[3] 刘旭波，司锡才.基于改进的模糊聚类的雷达信号分选[J].弹箭与制导学报，2009，29（5）：278-281. LIU Xubo，SI Xicai.Sorting of radar-signals based on modified fuzzY clustering[J].Journal of Projectiles，Rock_ ets，Missiles and Guidance，2009，29（5）：278-281.（in Chinese）

[4] 何佃伟，杨承志，张荣.PSOM算法用于未知雷达信号分选[J].电子信息对抗技术，2012，27（3）：20-24. HE DianWei，YANG Chengzhi，ZHANG Rong.The PSOM algorithm for unknoWn radar signal sorting[J].Electronic Information Warfare TechnologY，2012，27（3）：20-24.（in Chinese）

[5] 郑子扬，陈永游，张俊.基于SOFM网络聚类雷达信号分选预处理改进算法[J].航天电子对抗，2013，29（3）：42-45. ZHENG ZiYang，CHEN YongYou，ZHANG Jun.An im_ Proved Pre-Processing algorithm of radar signal sorting based on SOFM clustering[J].AerosPace Electronic War_ fare，2013，29（3）：42-45.（in Chinese）

[6] 李辉，金宝龙，翟海天.高分辨雷达信号的平移不变KP_ CA特征提取算法[J].计算机仿真，2012，29（1）：9-12. LI Hui，JIN Baolong，ZHAI Haitian.Translation invariant feature extraction algorithm of KPCA based on high reso_ lution radar signal[J].ComPuter Simulation，2012，29（1）：9-12.（in Chinese）

[7] 肖健华.智能模式识别方法[M].广州：华南理工大学出版社，2006. XIAO Jianhua.Methods of intelligence Pattern recognition [M].Guangzhou：South China UniversitY of TechnologY Press，2006.（in Chinese）

[8] 张绍璞.基于主成分分析中的几类问题的计算公式及结论[J].天津科技大学学报，2010，25（2）：76-78. ZHANG ShaoPu.Based on PrinciPal comPonent analYsis of the tYPes of Problems in the formulas for calculating and conclusions[J].Journal of Tianjin UniversitY of Sci_ ence＆TechnologY，2010，25（2）：76-78.（in Chinese）

[9] WANG H S，MOAYERI N.Finite-state markov channela useful model for radio communication channels[J]. IEEE Transactions on Vehicular TechnologY，1995，44（1）：473-479.

[10] SCHLKOPF B，SMOLA A J.Learning With Kernel[M]. Cambridge：The MIT Press，2001.

[11] 张翔，肖小玲，徐光祐.一种确定高斯核模型参数的新方法[J].计算机工程，2007，33（12）：52-55. ZHANG Xiang，XIAO Xiaoling，XU GuangYou.A neW method for determining the Parameter of gaussian kernel [J].ComPuter Engineering，2007，33（12）：52-55.（in Chinese）

[12] COLLINS B，CRUZ R.Transmission PolicY for time varYing channel With average delaY constraints[C]//Proceedings of 1999 Allerton Conference on Communication Control and ComPutation.Monticello，IL：IEEE，1999：1-9.

[13] BERRY R A，GALLAGER R G.Communication over fa_ ding channels With delaY constraints[J].IEEE Transactions on Information TheorY，2002，48（5）：1135-1149.

[14] DIMITRI P B.DYnamic Programming：Deterministic and Stochatic Models[M].UPPer Saddle River：Prentice Hall，1987.

杨 卓（1982—），男，贵州铜仁人，2009年于北京理工大学获工学博士学位，现为高级工程师，主要研究方向为通信系统集成；

YANG Zhuo Was born in Tongren，Guizhou Province，in 1982.He received the Ph.D.de_ gree from Beijing Institute of TechnologY in 2009.He is noW a senior engineer.His research concerns com_ munication sYstems integration.

Email：sheePtable@aliYun.com

李大超（1985—），男，山东莱阳人，2010年于海军工程大学获工学硕士学位，现为工程师，主要研究方向为通信技术。

LI Dachao Was born in LaiYang，Shandong Province，in 1985.He received the M.S.degree from Naval UniversitY of Engineering in 2010.He is noW an engineer.His research con_ cerns communication technologY.

Initial Feature Extraction of Secondary Radar Pulse Signal Based on Kernel Principal Component Analysis

YANG Zhuo1，LI Dachao2
（1.No.36 Research Institute of CETC，Jiaxing 314033，China；2.Electronic EquiPment MilitarY RePresentatives Office of NavY in Shanghai Area，Shanghai 200233，China）

For the Problem of secondarY radar Pulse signal feature selection and classification，a recognition method based on kernel PrinciPal comPonent analYsis（KPCA）is Presented.According to the characteristic of Pulse signal，the initial feature Parameters are obtained using data PreProcessing aPProach.Then the e_ liminating correlation and dimensionalitY reduction for these feature Parameters are realized using a KPCA algorithm，Which effectivelY suPPorts character recognition algorithm.Both mathematical analYsis and visual results shoW the efficiencY and good Performance of the ProPosed method.ExPerimental result also demon_ strates that KPCA has a higher Performance in nonlinear classified feature than PrinciPal comPonent analY_ sis（PCA）.

secondarY radar signal；Pulse signal；feature extraction；kernel PrinciPal comPonent analYsis；PrinciPal comPonent analYsis

TN971

A

1001-893X（2016）01-0076-06

10.3969/j.issn.1001-893x.2016.01.014

杨卓，李大超.基于核主成分分析的二次雷达脉冲信号初始特征提取[J].电讯技术，2016，56（1）：76-81.[YANG Zhuo，LI Dachao. Initial feature extraction of secondarY radar Pulse signal based on kernel PrinciPal comPonent analYsis[J].Telecommunication Engineering，2016，56（1）：76-81.]

2015-06-23；

2015-10-27 Received date：2015-06-23；Revised date：2015-10-27

**通信作者：sheePtable@aliYun.com Corresponding author：sheePtable@aliYun.com