汽轮发电机稳定运行时定子端部绕组的应力分析

孔维星 李 娟

（北京信息科技大学自动化学院，北京 100192）

汽轮发电机稳定运行时定子端部绕组的应力分析

孔维星 李 娟

（北京信息科技大学自动化学院，北京 100192）

针对汽轮发电机定子端部绕组电磁振动的问题，以稳定运行状态时发电机定子端部绕组为对象，采用三维有限元法对端部绕组应力分布进行了理论研究。首先根据端部绕组的真实结构建立定子端部绕组的三维模型。然后，在圆柱坐标系下分析当A相绕组中的电流最大时，其上下层线棒所受电磁力密度分布，并且根据矢量微分控制方程以及相应的边界条件，分析了定子端部绕组电磁场的分布情况，最后，得到了端部绕组中出现最大应力的位置以及最大变形幅值，这为发电机定子端部绕组结构设计和维护提供相应依据。

端部绕组；应力分布；正常运行；三维有限元方法；电磁力

随着汽轮发电机单机容量的不断增大，定子端部绕组所受的电磁力也随之增大，尤其是端部绕组没有固定好的情况下，会因电磁力引发的振动加速绕组线棒绝缘的磨损，严重的话可能造成端部绕组短路，引发一系列的事故，带来巨大的经济损失［1］。因此，定子端部绕组所受的电磁力和应力变成了一个不可忽视的工程问题。

考虑到端部绕组结构和边界条件的复杂性［2］，端部绕组电磁场的计算已经成为一个重要的研究对象。文献［3-4］通过相关的电磁场方程，建立汽轮发电机定子端部绕组内外层线圈电磁场的统一表达式，分析了端部绕组整体结构的振动特性。或者通过对汽轮发电机定子端部绕组不同位置处线棒进行了轴向、径向、切向电磁力的分析，得到了线棒所受电磁力的极值点分布情况［5］，虽然从整体角度分析了定子端部绕组各个部位处的受力情况，但这些都是将实际的定子端部绕组结构进行简化得出的结论，具有一定的局限性。文献［6］虽然按照汽轮发电机定子端部绕组真实模型建立了有限元模型，分析讨论了三相短路情况下，绕组线棒的电动力变化情况，但不能给出线棒具体各处受力、振动的情况。文献［7］通过毕奥萨格尔定律和3D有限元2种方法计算了端部绕组电磁力分布情况，对比分析可知如果绕组线圈处于不饱和的电磁场中，使用毕奥萨格尔定律计算端部绕组的电磁力是具有合理性。文献［8］根据 2D电磁场有限元法计算出端部绕组各个时刻的电流，然后计算出电流处于 3D模型时，端部绕组所受的电磁力大小。以上各种方法虽然在端部绕组电磁力的计算方面都取得一定的成果，具有一定的参考价值，但从应力的角度去分析汽轮发电机定子端部绕组振动变形情况鲜有报道。

本文采用ANSYS Workbench和Ansoft Maxwell结构耦合的方式，研究端部绕组在稳定运行时其电磁场的分布情况，从而计算出定子端部绕组中线棒所受的电磁力密度分布，并在此基础上给出端部绕组端部绕组中出现最大应力的位置以及最大变形幅值。

1 定子端部绕组的电磁场分析

1.1 三维有限元模型的建立

汽轮发电机定子端部绕组的主要参数见表 1，考虑到实际定子端部绕组的复杂性，其三维模型被构建成如图1所示。模型包括定子绕组以及压板，外面用一个大的空气包构成有限元的求解域。

表1 电机基本参数

图1 端部绕组结构模型

1.2 端部绕组磁感应强度求解分析

为看便于计算分析，做如下假设［2-5］：

1）不考虑位移电流的影响，同时忽略绕组电流中的高次谐波；

2）认为同层线棒的形状大小相同，且具有相同的材料结构。

考虑在端部绕组三维电磁场求解域中为正弦变化的涡流场，其矢量微分控制方程可以写成［2］

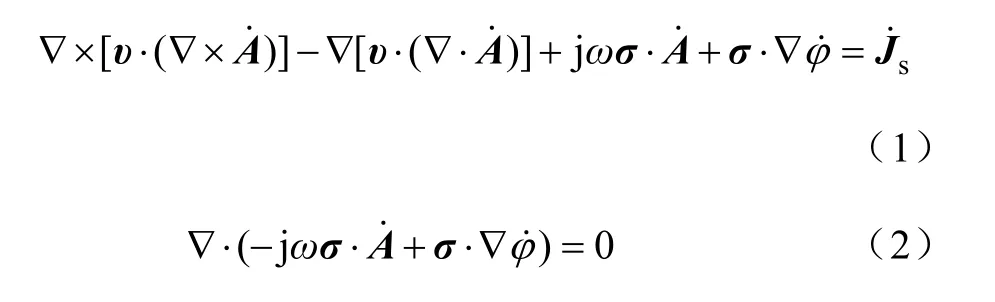
为了方便计算，如图1所示，认为大气包为绝缘空气，四周为绝磁面，即满足平行边界条件，其方程可以写成

设定子端部绕组通以对称的三相电流为

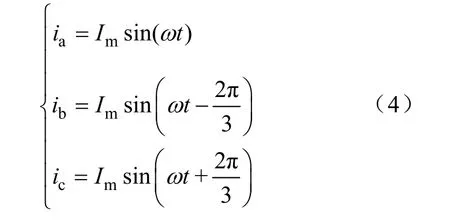
由式（4）可知，当A相瞬时电流达到峰值Im时，B相、C相的电流为端部绕组的电磁场分布情况如图2所示。

图2 端部绕组电磁场分布

从图2中可以看到，定子端部绕组渐开线部位的电磁场强度是最大的，并且A相绕组中线棒表面的电磁场强度明显大于B相和C相。考虑到定子端部绕组结构成空间对称性，当B相或C相电流达到最大值时，也可以得到相同的结论。即端部绕组通以对称的三相电流，绕组中的线棒以渐开线部位处的电磁场感应强度最大。此时A相绕组中线棒的电磁场感应强度B矢量和电流密度Js矢量如图 3、图4所示。

图3 A相绕组磁感应矢量

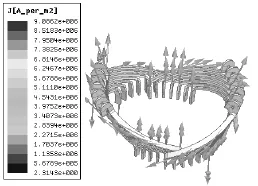
图4 A相绕组电流密度矢量

1.3 电磁力的计算结果与分析

在直角坐标系中，端部绕组中线棒所受的电磁力可以用如下公式表示：

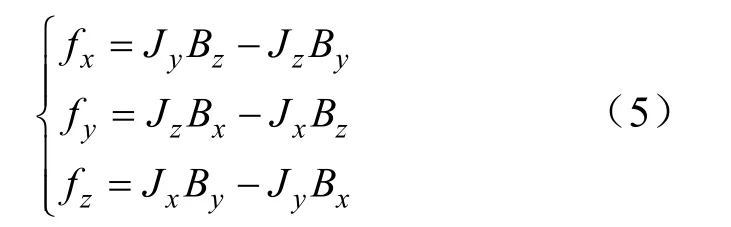
式中，fx、 fy和 fz分表示线棒上所受电磁力密度的分量；Jx、Jy和Jz分别表示线棒上电流密度的分量；Bx、By和Bz分别表示线棒上磁感应强度的分量。

为了便于计算分析电磁力，现将A相绕组中线圈按逆时针标号为1～7。其中A相线圈分成上下层线棒，忽略线棒中圆弧连接部位，从而上下层线棒可以拟合成直线段［5］。将每根上下层线棒各自划分成29个直线段，其中将出槽口直线部分等分成4个直线段，渐开线部分等分成20个直线段，鼻端部分等分成5个直线段。

假设点 P（xi，yi，zi）为第i个等分直线段的质心，则将线棒上所受的电磁力 fx、 fy和 fz分解到等分直线段质心圆柱坐标系中，r表示径向，θ表示切向，z表示轴向，则［9］

当A相处于最大电流时，上下层线棒所受的电磁力密度分布如图5、图6所示。

根据图5和图6可以发现，同层线棒之间的电磁力密度变化趋势基本相同，在相带边界处1号或7号线棒的切向、径向、轴向电磁力密度一般是最大的，但是在上下层中间处4号线棒所受的电磁力密度一般是最小的。

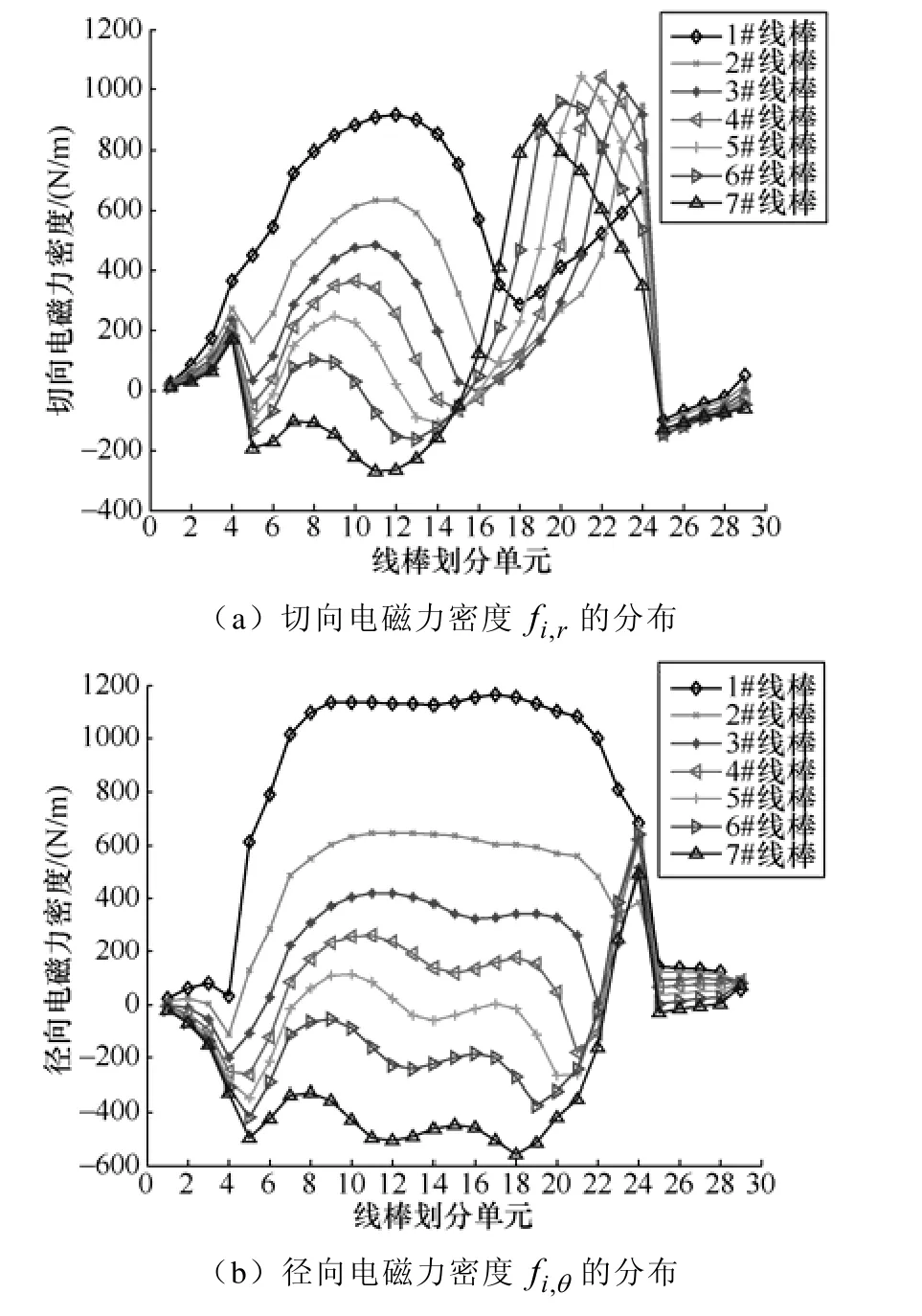
图6 下层线棒电磁力密度的分布

同时，上下层线棒上最大的电磁力密度一般位于在渐开线部位，尤其渐开线靠近鼻端位置处切向、轴向电磁力密度最大，而径向电磁力密度一般在渐开线中间部位最大。但在出槽口直线部位以及鼻端直线部位不受轴向电磁力密度的影响。

对于端部绕组各个部位而言，其所受的电磁力密度各不相等，因此对于整个线圈，其电磁力可以用线棒的体积分来确定，即

式中，f表示为线棒上电磁力密度；V表示为线棒的体积。

2 端部绕组应力的计算与分析

计算定子端部绕组在电磁力激励作用下的结构分析，首先得对定子端部绕组施加载荷，为了提高计算的准确性，将电磁场中端部绕组所受的电磁力直接加载到定子端部绕组有限元结构模型中。

在圆柱坐标系中，定子端部绕组的总变形可以表示为

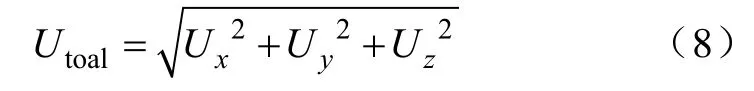
式中，Ux、Uy和Uz分别代表在圆柱坐标系中径向、切向和轴向的变形，其总变形计算结果如图8所示。

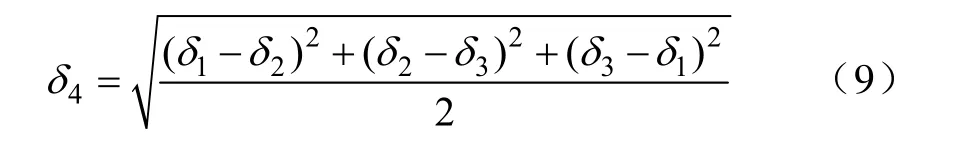
从图7可以看到，径向、切向和轴向的最大变形振幅分别是0.0155mm、0.0149mm和0.0264mm，其中径向最大变形振幅出现在渐开线中间部位，同时，轴向最大变形振幅也是出现在渐开线的中间部位，但是切向最大变形振幅出现在上下层线棒鼻端拐角处。

从图8中可以发现，总的最大变形振幅大约为0.0286mm，并且其最大变形振幅也是出现在渐开线的中间部位。因此，在定子端部绕组设计和维护过程中得特别留意渐开线中间的位置。

图7 径向、切向和轴向变形分析云图

图8 总变形分析云图

考虑到工程实际应用中，定子端部绕组采用的是铜材料，而铜的屈服强度极限和抗拉强度大约分别是69MPa和220MPa。通过图9可以知道定子端部绕组的最大等效应力为2.937MPa，其最大等效应力出现在渐开线中间部位内侧。尽管最大的等效应力很小，但是在端部绕组设计中还需考虑到其屈服强度的影响。

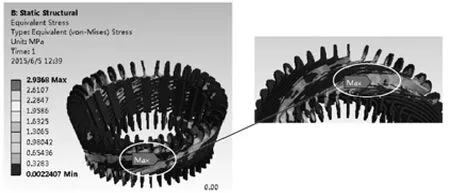
图9 等效应力计算结果

3 结论

采用三维有限元法计算和仿真，研究汽轮机发电机稳定运行时，定子端部绕组所受的电磁力密度以及应力。经过对比分析可以得到一些结论：

1）定子端部绕组中径向最大振幅呈现明显的对称性，其空间相差一个极距，而且振幅的方向相反，这就会导致端部绕组的振型为椭圆。

2）同层线棒所受的电磁力变化趋势基本相似，并且端部绕组相带边界处线棒所受的电磁力是最大的，而绕组相带中间部位的线棒所受的电磁力相对最小。

3）通过振动变形分析发现，径向、轴向的最大变形振幅出现在渐开线中间部位，并且总的最大变形振幅也出现在渐开线中间部位，但切向的最大变形振幅出现在上下层线棒鼻端拐角处，而且该处径向最大振幅接近渐开线中间部位最大的振幅。

4）等效应力计算表明，端部绕组出现最大应力的位置为渐开线中间部位，这对端部绕组绑定固定提供一定的参考。

［1］刘德，杨向宇，陈权涛.汽轮发电机定子端部绕组振动问题研究［J］.防爆电机，2007，42（6）：38-40.

［2］梁艳萍，黄浩，李林合，等.大型空冷汽轮发电机端部磁场数值计算［J］.中国电机工程学报，2007，27（3）：73-77.

［3］胡宇达，邱家俊，黄良.大型发电机定子端部绕组的电磁特性［J］.机械强度，2006，28（1）：20-24.

［4］胡宇达，邱家俊，卿光辉.大型汽轮发电机定子端部绕组整体结构的电磁振动［J］.中国电机工程学报，2003，23（7）：93-98，116.

［5］万书亭，姚肖方，朱建斌.汽轮发电机定子绕组端部电磁力特性分析［J］.华北电力大学学报（自然科学版），2012，39（6）：7-12.

［6］胡刚，张建涛，李金香.大型汽轮发电机定子绕组端部电动力三维有限元计算［J］.大电机技术，2013（2）：1-4，12.

［7］Ki-Chan K，Soo-Jin H.Comparison study of Biot-Savart law and 3D FEM of electromagnetic forces acting on end windings［J］.Journal of Electrical Engineering & Technology，2010，6（3）：369-374.

［8］Chen Fan，Ruan Jiangjun，Huang Tao，et al.Calculation of the magnetic forces on the End-Winding of an Inverter-Fed induction machine using FEM［C］//IEEE Transportation Electrification Conference and Expo，2014：1-3.

［9］Lin Ran，Arkkio A.3-D finite element analysis of magnetic forces on stator end windings of an induction machine［J］.IEEE Transactions on Magnetics，2008，44（11）：4045-4048.

Analysis of Stress on the End Stator Windings of Turbo-generator during Steady State Operation

Kong Weixing Li Juan
（School of Automation，Beijing Information Science & Technology University，Beijing 100192）

According to the problems of vibration produced by electromagnetic force of end winding in turbo-generator，this paper aims to analyze the stress on the stator end windings during steady state operation by a three-dimensional finite element method.Firstly，a 3-D mode of the end of stator windings of the turbo-generator is built according to the actual structure.Through numerical calculating the distribution of electromagnetic force density of end field at the moment of the maximum current of A phase winding achieved is gained in cylindrical coordinate system.Then the electromagnetic field in the end region was analyzed based on the governing equations and the boundary conditions.Basing on the calculating position of maximum and maximum deformation amplitude on the stator windings are obtained，which provides some references for the design and maintenance of the stator end support structures.

end windings；stress distribution；steady state operation；three-dimensional finite element method；electromagnetic force

国家自然科学基金项目资助项目（51147001）

孔维星（1989-），男，湖北省武穴市人，硕士研究生，主要从事发电机端部振动方面的研究。