常州市“十三五”期间经济增长率预测

何勇

（常州市统计局，江苏常州　213022）

常州市“十三五”期间经济增长率预测

何勇

（常州市统计局，江苏常州213022）

本文立足常州市改革开放以来的统计数据，综合使用HP滤波法、劳动生产率法、随机时间序列模型法三种计量模型方法科学预测常州市“十三五”期间经济增长率，为政策制定和决策参考提供数据支撑。

常州；经济增长率；预测

今年是常州市“十三五”的开局之年，科学预测常州市“十三五”期间潜在经济增长率，对于实现经济社会发展目标至关重要。本文侧重通过统计数据建立计量模型的方法，综合使用HP滤波法、劳动生产率法、随机时间序列模型法三种方法来科学预测常州市未来潜在经济增长率。

一、基于HP滤波法的ARIMA预测

潜在产出是分析宏观经济运行态势、制定经济政策的重要工具和依据，在测算潜在经济增长率的众多方法中，HP滤波法是一种相对简单、应用普遍的方法，Hodrick和Prescott认为经济变量既不是永恒不变也不是随机变动，其趋势是缓慢变动的。

通过HP滤波法剔除宏观经济运行的周期性波动后得到潜在经济增长率，这种方法的优点在于依赖的指标少，但是经济学理论支撑不够充分，只能说明数据变化的趋势，难以从中得出具体的政策含义和经济学规律，属于典型的“数据挖掘”方法。本文使用HP滤波法进行预测的目的是从增长率数据变化本身推测常州市“十三五”潜在经济增长率的可能区间，为其他预测方法提供参考。

（一）HP滤波结果

对1979-2015年经济增长率的HP滤波结果见图1。滤波结果表明，改革开放以来常州市潜在经济增长率维持在9%-15%的区间。按照“波谷-波峰”划分方法，常州市潜在经济增长率的长期趋势可以分为四个周期：第一个周期是1979-1995年，潜在经济增长率的波动区间在9.98%-14.96%之间；第二个周期是1996-2000年，潜在经济增长率的波动区间在14.44%-13.13%之间；第三个周期是2001-2006年，潜在经济增长率的波动区间在13.14%-13.56%之间；第四个周期是2007年至今，潜在经济增长率由2007年的13.42%回落至2015年的9.95%。

图1　HP滤波后常州市潜在经济增长率（Trend）

（二）对潜在经济增长率的ARIMA预测

ARIMA（p，d，q）模型是一类常用的随机时序模型，它是一种精度较高的时序短期预测方法，其基本思想是：某些时间序列是依赖于时间t的一组随机变量，构成该时序的单个序列值虽然具有不确定性，但整个序列的变化却有一定的规律性，可以用相应的数学模型近似描述时间序列的过去值、现在值来预测未来值。

由于ARIMA模型要求序列具有平稳性，因此对经过HP滤波得出的1979-2015年潜在经济增长率进行ADF单位根检验，结果表明该组数据在二阶差分后是平稳序列，因此在ARIMA模型中，d选择2；根据对二阶差分后的序列进行自相关分析，偏自相关系数在k=2后很快地趋于0，所以p选择2；自相关系数截尾趋势不明显，因此q的确定需要根据LM检验和AIC、SIC准则进行选择，通过运算处理及结果判断，ARIMA（2，2，2）更为适合本模型。

利用ARIMA（2，2，2）对2016-2020年的潜在经济增长率进行预测，预测结果表1，结果显示2016-2020年常州市潜在经济增长率下降态势较为明显，由“十二五”初期12.04%的潜在增长率下降到“十三五”末期7.48%左右的增长水平，远低于改革开放后历年的增速。另外，由于受长期经济增长趋势影响，ARIMA模型预测值在2016年和2017年会略微偏高。

表1　经济增长率的ARIMA模型预测结果

二、基于劳动生产率的预测

在发展方式一定的前提下，经济增长速度主要由各种生产要素的供给决定，其中，相比于资本、土地、技术等生产要素，劳动力要素的波动性是最小的，因为劳动力的数量主要由人口规模决定，而人口规模在短期内很难发生巨大变化，劳动力的质量主要由教育决定，而教育又是一个长期的投资过程，人口平均受教育年限在短期内也不会发生巨大改变，因此，从波动性最小的劳动力数据出发，可得到相对可靠的潜在经济增长率趋势预测。

（一）劳动年龄人口及全社会从业人员的预测

根据常州市第六次人口普查资料查得2010年各年龄的人口数和死亡率数据，根据温勇（2006）《人口统计学》方法可推算n年后除0到n-1岁以外的各年龄人口数，具体的计算公式为：

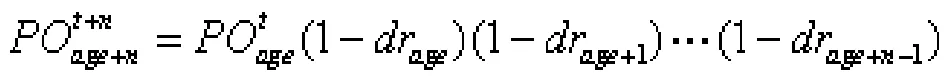
表2　15-64岁劳动年龄人口预测结果

预测结果表明2012年常州市的劳动年龄人口数量出现了下降，之后绝对值呈现逐年递减趋势，这个预测结果和国家统计局2013年公布的全国数据相一致，“2012年我国15—59岁劳动年龄人口在相当长时期里第一次出现了绝对下降，比上年减少345万人”，常州市和全国劳动年龄人口在2012年同时出现拐点印证了人口红利优势的消退。本文假设全社会从业人员绝对值变化和劳动年龄人口呈现高度正相关关系，根据2012-2020年劳动年龄人口当年变化率推算2012-2020年的全社会从业人员，具体的计算公式为：

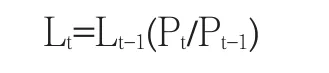
上式中，t为年份，L为全社会从业人员，P为15-64岁劳动年龄人口。

表3　经测算的2012-2020年全社会从业人员

（二）劳动生产率和潜在经济增长率预测

使用按1978年不变价格计算的常州市地区生产总值数据与当年全社会从业人员数相除的方法，可分别计算历年按可比价格计算的常州市平均劳动生产率，1978-2015年常州平均劳动生产率变化轨迹类似指数曲线或三次多项式曲线，分别对两种曲线拟合方程。令t为自1978年开始计数的年份，并令Xt为第t年的常州市平均劳动生产率，则有：

模型Ⅰ——指数函数：

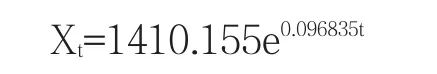
（修正的R2=0.996476）

模型Ⅱ——三次多项式函数：

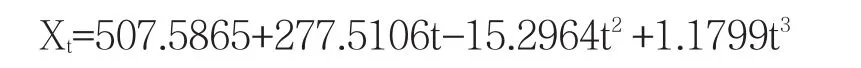
（修正的R2=0.997717）

经观察，模型Ⅱ修正的R2优于模型Ⅰ，故使用模型Ⅱ预测2016-2020年的平均劳动生产率，将这些预测值与相应年份的全社会从业人员的测算值相乘，得到按1978年不变价格计算的未来各年份常州市地区生产总值，据此可计算经济增长率预测值，计算结果列于表4。

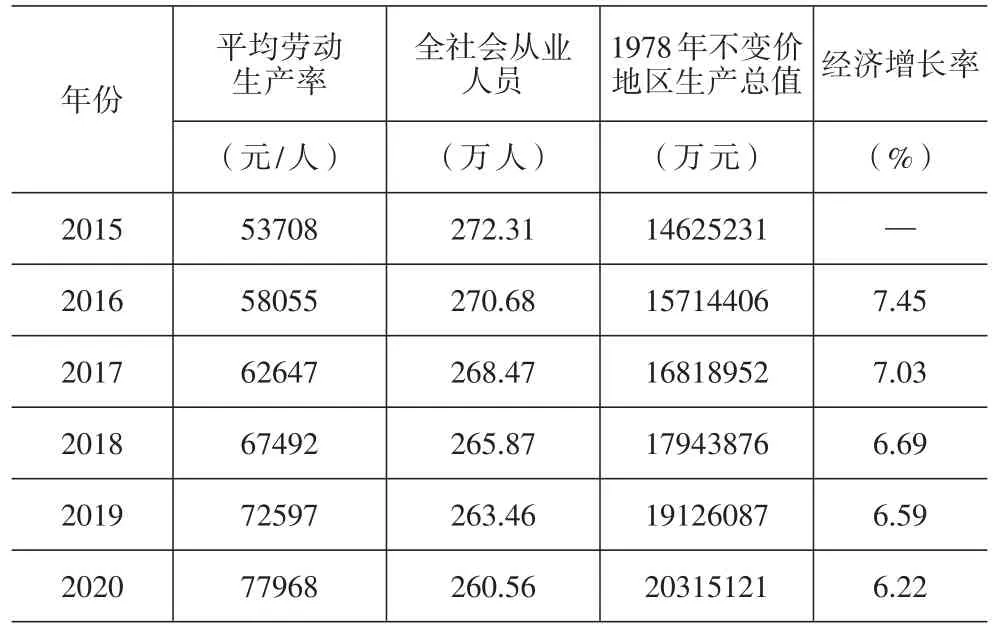
表4　常州市平均劳动生产率和经济增长率预测

结果显示，“十三五”期间常州市经济增长速度在6.22%-7.45%之间，较“十二五”期间9.2%-12.2%的增速区间明显下降。

三、基于生产函数的分析和ARMA的预测

生产函数代表了产出与要素投入之间的技术关系，从生产函数出发估计潜在产出的方法已经在发达国家广泛应用，具有明确的经济理论基础和基本分析框架，预测结果具有较为丰富的政策含义。这种方法的缺点主要在于资本、劳动力等外生变量指标的计算方法以及全要素生产率的函数形式还存在很大争论，对各种外生变量的预测也难免带有一定的主观成分，这降低了分析和预测的客观性和准确度。

（一）模型设定

按照索洛的经济增长理论分析框架，采用柯布—道格拉斯生产函数：Y=AKαLβ，其中Y表示总产出、K表示资本存量、L表示人力资本、A表示技术进步，α和β分别代表K和L的产出弹性系数。

假设规模报酬不变，α+β=1，于是生产函数可以进一步简化为如下形式：Y/L=A（K/L）α，简化后的模型变成一元模型，消除了多元共线性可能造成的干扰，模型得到一定优化。Y/L是人均产出，K/L是人均资本投入。将上式两边进行对数化处理，得到：

（二）数据的选取

1.Y的确定：Y代表总产出，本文取1978-2014年的常州市地区生产总值按1978年为不变价折算后的数据。

2.L的确定：人力资本不仅包括劳动力人数，还包括劳动力人群的年龄结构、性别结构、受教育情况和技能水平等多种因素，但由于资料的易得和有限性，本文人力资本取用的是1978年来的常州市全社会从业人员数。

3.K的确定：资本存量K根据国际上通常采用的方法，采用永续盘存法估算出从基期到报告期以来的固定资本形成存量。用公式表示为：Kt= It/Pt+（1-δ）Kt-1，其中，Kt表示第t年年末实际资本存量；It表示第t年固定资产投资完成额；Pt为固定资本投资价格指数；δ表示重置率；Kt-1表示上一年年末实际资本存量。

It和Pt的确定：It使用常州市1978-2014年的固定资产投资完成额。Pt为以1978年为基期的固定资产投资价格指数，由于缺乏常州市相关数据，本文利用《2015江苏统计年鉴》和《中国国内生产总值核算历史资料1952－1995》中的数据推算出以1978年为基期的各年固定资产投资价格指数，进而得出历年以1978年为基期的不变价投资额It/Pt。

δ的确定：永续盘存法考虑资本品的效率在各期呈几何下降趋势，我们用固定资产综合折旧率来替代重置率。根据国内外研究经验，δ的取值基本在5%-10%之间，本文结合上海市和无锡市处理折旧率的经验，取常州市1978-2000年的δ为5%，2000年以后为6%。

基年实际资本存量K0的估计：根据张军（2003）《中国省际物质资本存量估算》所提供的数据，推得江苏省1978年的初期资本存量为216.46亿元，根据1978年常州市工业经济份额占全省比重推算常州市1978年初期资本存量K1978=19.79亿元。

至此，已经确定了It、Pt、δ、K0的取值，根据永续盘存法求得1978-2014年的资本存量K。

（三）方程拟合

利用最小二乘法对生产函数方程进行回归分析得到：

LOG（Y/L）=2.0050+0.7440LOG（K/L）+［AR（1）= 1.2853，AR（2）=-0.4841］

回归方程参数估计结果显示，修正后的R2= 0.9975，F统计值为4450.68，D.W.≈2，各个自变量的收尾概率小于显著性水平0.01，拟合优度较好，检验效果显著。

（四）数据实证分析

由于假设规模报酬不变，α+β=1，已知α= 0.74，得到β=0.26，说明α和β每增长1%分别能带来0.74%和0.26%的地区生产总值增长。根据1978-2014年的地区生产总值（Y）年均增速、资本存量（K）年均增速、人力资本（L）年均增速，进而可以推算出由技术进步（A）、资本存量（K）、人力资本（L）对常州市地区生产总值的贡献率，详见表5

表5　1978—2014年常州市各要素的贡献率

从表5我们可以看出，1978-2014年经济增长主要由资本投入带动，资本贡献率为92.16%，其次由全要素组成的技术进步拉动，贡献率为4.28%，由于改革开放30多年来全社会从业人员年均增速仅1.77%，所以人力资本贡献率较小，为3.26%。

（五）“十三五”经济增长率预测

由于缺乏相关数据导致对索洛模型中外生变量推算困难，若是单纯利用回归方程推算外生变量可能导致总产出Y的预测结果不理想，所以本文仅对1978-2014年不变价地区生产总值数据作随机时序分析，为减少数据的波动性对序列进行指数化处理，再对处理过后的时间序列建立ARMA模型，通过运算处理及结果判断，ARMA（1，1）模型最为合适，具体预测结果见表6。

表6　基于ARMA模型对常州市地区生产总值增长率的预测

四、主要结论

综合上述三种模型预测方法，常州市“十三五”期间经济增速将呈现下降走势。其中，HP滤波法预测精度较差，主要目的是预测数据趋势，经济增速将由9.42%下降至7.48%，平均值为8.43%；劳动生产率法预测结果表明常州市经济增速将由7.45%下降至6.22%，平均值为6.80%；基于生产函数法的结果表明改革开放以来常州市经济增长主要由物质资本驱动，其次为技术进步和人力资本驱动，三者的贡献率分别为92.16%、4.28%和3.56%，利用ARMA模型对总产出的预测可知，“十三五”期间常州市的经济增速将由8.20%下降至5.49%，平均值为6.78%。虽然三种预测结果都证明“十三五”期间常州市经济增长率将出现下降，但是这种趋势符合经济长期高速增长后的阶段性特征，是今后经济发展的新常态，并且按照这种预测均速发展，到2020年常州市也能如期实现地区生产总值比2010年翻一番的规划目标。

（责任编辑：高萍萍）