整式加减中的“整体思维”

杨春鸟

整式加减中的“整体思维”

杨春鸟

同学们都知道，要把杂七杂八、大小不一的小东西一次搬走是件很麻烦的事，但如果将它们集中放在一个箱子里再搬走就省事多了.这种思想就叫整体思维.日常生活是这样，学习数学也不例外，整体思维常常会避繁就简，使问题得到巧妙解决.现结合整式加减中的具体实例，我们来看一下整体思维方法在解题中的灵活运用.

一、整体加减

例1已知m2-mn=21，mn-n2=-12.求m2-n2与m2-2mn+n2的值.

【解析】由于本题直接去求m、n值不易，通过观察可以发现m2-mn+mn-n2=m2-n2，所以m2-n2=21-12=9.同理，m2-mn-（mn-n2）=m2-2mn+n2，所以m2-2mn+n2=21+12=33.

本题通过整式的“整体”加减，达到求整式的值的目的，避免了分别求m、n值.

二、整体代入

例2若m、n互为倒数，则mn2-（n-1）的值为_____.

【解析】根据m、n互为倒数，可得mn=1，

因为mn2-（n-1）=（mn）n-n+1，把mn=1代入，得n-n+1=1.所以mn2-（n-1）=1.

例3已知3y2-2y+6=8，求整式y2-y+1的值.

【解析】已知3y2-2y+6=8，即3y2-2y=2，而y2-y+1可以变形为（3y2-2y）+1，把3y2-2y= 2代入，可得（3y2-2y）+1=2.

以上两例，通过对代数式的变形，使其出现已知中的“整体”部分然后再“整体”代入.这类问题关键是思考将哪部分看成一个整体，比如例3中如果将y2看成一个整体，同学们想一想该如何解决呢？

三、整体平移

例4如图，在长a米，宽b米的长方形地面上修建两条宽为c米的道路，余下部分作为草坪，则草坪面积是多少？

【解析】求草坪面积的常规思路为长方形面积减去道路面积，再加上两条道路重叠部分的面积即（ab-ac-bc+c2）平方米.

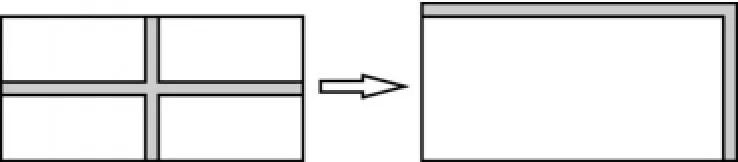
现结合图形，把两条道路靠边平移，这样，分散的草坪就转化为一个长为（a-c）米，宽为（b-c）米的长方形，其面积为（a-c）·（b-c）平方米.

对比这两种方法，易见用“整体平移”后的方法更简捷，启示我们在解题过程中，不要只着眼于“局部”，还要着眼于“整体”.

四、整体分割

例5如下图，在正方形网格中按规律填阴影，根据此规律，则第n个图中阴影部分小正方形的个数是_____.

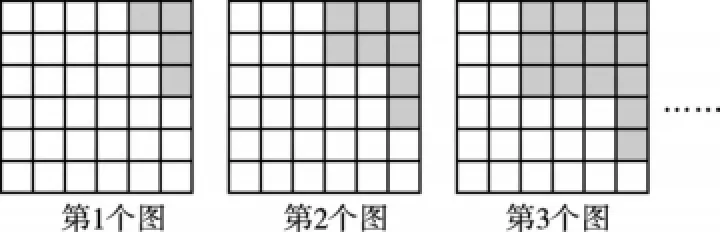
【解析】如果单纯看每个图形阴影部分小正方形的个数，很难看出其中隐含的规律.若把阴影部分进行整体分割，分割成两个长方形，其中一个长方形包含的阴影小正方形的个数是2，另外一个长方形与整体图形个数呈规律变化，可以看出第n个图中阴影部分小正方形的个数是n（n+1）+2.

此题利用对图形的“整体”分割，使“数形”规律更明确，从而优化了问题的特征与解题方向.另外，本题还有不同的“整体”分割的方法，有兴趣的同学可以互相探讨一下.

五、整体覆盖

例6已知正方形的边长为a，以各边为直径在正方形内画半圆，则所围成的阴影部分（如下图）的面积为_____.

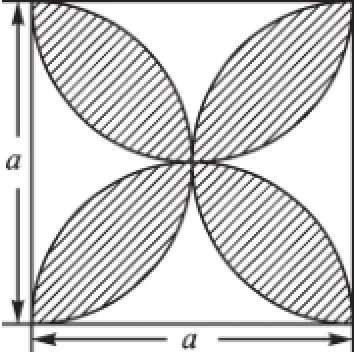
【解析】观察图形，四个半圆覆盖边长为a的正方形，四个半圆重叠部分即是阴影部分的面积.所以，阴影部分的面积为四个半圆面积之和减去正方形面积：

本题关键是通过观察图形的形成，寻找“整体”覆盖的基本图形即半圆，从而找出问题突破口.

（作者单位：江苏省海门市海南中学）

扫码学习更多整体思想在代数式中的应用