基于EEMD和PSO-SVM的滚动轴承故障诊断

陈园艺，孙建平

(华北电力大学 控制与计算机工程学院，河北保定071003)



基于EEMD和PSO-SVM的滚动轴承故障诊断

陈园艺，孙建平

(华北电力大学 控制与计算机工程学院，河北保定071003)

为实现滚动轴承故障的精确诊断，提出一种基于集成经验模态分解与粒子群算法优化的支持向量机的故障诊断方法。利用EEMD方法分解振动信号，依据经验选取合适的内禀模态函数进行能量值及包络谱特征幅值比等故障特征参量的计算，构建滚动轴承故障特征向量，然后基于少量不同故障部位及故障程度的样本，利用粒子群算法对支持向量机进行参数优化，进而训练样本并建立故障模型，最后对测试样本进行故障诊断，观察该方法的诊断效果。实验表明，该方法可对多种不同故障状态进行诊断，且分类精度高，证明了振动分析与智能算法结合的方法可有效实现滚动轴承的故障诊断。

滚动轴承；集成经验模态分解；粒子群算法；支持向量机；内禀模态函数

0　引言

滚动轴承是旋转机械设备中易受损的部件之一，它的寿命随机性大，失效时产生的振动和噪声会直接影响到机械设备的正常工作，使机械运行状态变差，快速定位轴承故障能缩短维修时间，提高机组的经济效益。随着机械设备逐渐向高速化、大型化和自动化方向发展，对滚动轴承的故障进行快速而准确地诊断也是目前机械故障诊断研究领域中的重点之一。

根据设备运行中的不同状态指标进行分类，目前滚动轴承故障诊断的常见方法有振动分析法、油液分析法、声信号分析法、温度分析法等，其中在大多数情况下，振动参数更能直接、准确、快速地反应机组运行状况，所以振动分析法也是机械故障诊断主要的工程应用方法。滚动轴承故障振动信号常表现为非平稳特征，这使得一些提取故障特征的传统方法在处理该类故障信号时存在一定的局限性，如傅里叶变换对信号在时域或频域的全局特性的描述不够全面，小波变换不具有自适应性[1]。文献[2]首次提出了经验模态分解方法(Empirical Mode Decomposition，EMD)，主要思想是将复杂的信号按不同时间尺度分解为一系列彼此正交的内禀模态函数(Intrinsic Mode Function，IMF)和余项之和，该方法在振动信号研究领域得到广泛应用，但也存在一些不足之处，如模式混叠、端点效应及包络线拟合问题等。文献[3]提出集成经验模态分解方法(Ensemble Empirical Mode Decomposition，EEMD)，借助高斯白噪声的特性，消除EMD的模式混叠现象。文献[4]提出分段3次HERMITE插值方法与基于斜率再优化的极值点延拓加窗函数法相结合，在解决欠包络和过包络问题的同时改善EMD的端点效应。文献[5]提出基于微分改进的EMD来改善传统EMD的混波问题。

本文将采用EEMD方法分解多种故障类型下的滚动轴承振动信号，依据经验选取合适的IMF分量，提取内禀模态能量值及内禀模态包络谱特征幅值比，构建故障特征向量，与基于粒子群算法优化的支持向量机结合，完成样本训练后，对滚动轴承进行多故障诊断。

1　EEMD

1.1EMD方法

EMD是一种具有自适应性的时频分析方法，它将原始信号分解为若干个相互正交的IMF分量之和，从而定义瞬时频率和瞬时幅值，非常适合用于处理非平稳、非线性信号。EMD分解过程中的基函数是依据信号本身产生的，而非小波分解等方法需要基于经验预选选择，分解所得的各个IMF分量包含不同的时间尺度和频率成分，这使得EMD具有多分辨率的特性，也决定了EMD方法的自适应性。每个IMF分量需满足2个条件：整段数据中，极值点与过零点的个数之差不超过1个；在任意时刻，由局部极大值点和局部极小值点分别构造的上下包络线相对于时间轴局部对称。

在此基础上，EMD对任意信号分解的具体步骤如下所示：

(1)找到信号x(t)的所有极大值点和极小值点；

(2)用3次样本插条方法构造上下包络线，计算均值，记为m(t)，计算x(t)减去m(t)后的值h(t)；

(3)判断h(t)是否满足IMF条件，如果满足则将h(t)看作第1个IMF分量c1(t)，否则将h(t)作为原始数据，重复步骤(1)至(3)直到满足IMF条件为止；

(4)将c1(t)从x(t)中分离出来，得到r(t)，判断r(t)是否仍能提取IMF分量，若能则将r(t)作为原始数据，重复步骤(1)至(4)，得到第2个满足条件的IMF分量c2(t)，否则终止；

(5)重复循环，当r(t)成为一个单调函数，循环结束。

此时已将一个复杂信号分解为若干个内禀模态函数和余量之和，如式(1)所示：

(1)

式中：c(t)表示IMF分量；n是分解得到的IMF分量的个数；r(t)表示余量，代表原始信号的平均趋势。

1.2EEMD方法

传统EMD方法存在一定的缺陷，如最为常见的模态混叠现象，是由于极值点分布不均匀或IMF不连续造成的。EEMD方法是在EMD方法的基础上改进得到的，高斯白噪声具有频率均匀分布的统计特性，可使信号在不同尺度上具有连续性，EEMD算法的实质即是通过在信号中加入白噪声来解决EMD分解的模态混叠问题。EEMD分解步骤如下：

(1)在原信号基础上多次加入幅值系数为k的白噪声序列ni(t)(i=1,2,…,m)，得到m个含有白噪声的新信号，如式(2)所示：

(2)

(2)对新信号xi(t)进行EMD分解，分别得到n个IMF分量，记为cij(t)(j=1,2,…,n)，余量记为ri(t)。

(3)计算各个新信号分解后所得IMF均值、余量均值，将其作为最终的IMF分量及余量结果，如式(3)、式(4)所示：

(3)

(4)

式中：cj(t)表示EEMD分解得到的第j个IMF分量；r(t)表示EEMD分解后的残余函数。

2　基于IMF分量的故障特征参量提取

对不同故障的滚动轴承振动信号进行EEMD分解后，得到若干个IMF分量。由于滚动轴承的故障信息多集中于高频带区，依据经验，选择频率较高的几个IMF分量进行故障特征参量的提取。

2.1内禀模态能量值

滚动轴承在发生不同类型的故障时，轴承其他部件会间断性撞击故障部位，激起不同程度的固有频率，显著表现即是随频率分布的能量会发生变化：正常时，振动信号的能量在各个频率带分布均匀；发生故障时，能量更集中于固有频率段，分布不均较为明显。由EEMD分解得到的IMF分量包含着原振动信号不同频带的信息，故障发生时，各个IMF分量能量值也将随之发生变化。提取内禀模态能量值作为故障特征参量，可在一定程度上区分故障类型[6,7]。各个IMF分量的能量如式(5)所示：

(5)

式中：c(t)代表IMF分量。

2.2内禀模态包络谱的特征幅值比

一旦在内圈、外圈滚动体及保持架等部位发生故障，内禀模态包络谱中相应故障特征频率处会出现谱峰。选择IMF分量的包络谱幅值比作为特征参量，可准确地反映滚动轴承的工作状况[8,9]。

对IMF分量进行HILBERT变换，进一步求得包络信号B(t)，如式(6)所示：

(6)

式中：H[c(t)]表示IMF分量的HILBERT变换。

对包络信号进行谱分析，依次得到IMF分量的包络谱。定义包络谱的特征幅值比如式(7)所示：

(7)

式中：A(fi)、A(fo)、A(fr)分别表示轴承在内禀模态包络谱中内圈、外圈、滚动体故障特征频率处的幅值。

3　基于粒子群算法优化的支持向量机

3.1支持向量机

支持向量机(Support Vector Machine，SVM)是CORTES和VAPNIK于1995年提出的一种基于统计学习理论的机器学习方法。它建立在统计学习理论的VC维理论和结构风险最小化的基础上，实现方法是通过非线性映射将低维空间的非线性分类转换为高维空间的线性分类，在追求经验风险最小化的同时也获得较好的推广能力，克服了神经网络的过学习及依据经验确定结构类型的固有缺陷。

设样本集为：(x1,y1),(x2,y2)，…，(xn,yn)，i=1,2,…,n，x∈Rd，y∈{-1,+1}。构造最优超平面：ωx+b=0，其中ω为系数向量，b为常数。引入松弛变量ζi，把寻找最优超平面问题转化为求解二次最优化问题，如式(8)：

(8)

式中：ζi表示噪声样本点与间隔之间的距离；C为惩罚因子，反映了对离群点带来的损失的惩罚力度。相应最优分类函数也如式(9)所示：

(9)

式中：辅助非负变量a为式(8)极值点处的LAGRANGE乘子。采用常见的RBF核函数作为分类核函数，如式(10)所示：

(10)

在解决滚动轴承的多故障识别问题时，往往需要构造多类分类器[10]。这里选取“一对一”的构造方法，即将一个k类问题两两组合，对每个组合构造一个SVM模型，每个SVM模型都成为上述的二分类问题，共有k(k-1)/2个SVM分类器，根据f(x)的符号判断出x属于两类中的哪一类，记该类一票，得票数最多的那一类为x在SVM判定下的所属类别。

3.2粒子群算法

粒子群算法(Particle Swarm Optimization，PSO)是一种能够快速收敛的全局搜索算法，它将待优化参数看做是n维搜索空间中的一群粒子，粒子均以一定的速度飞行，以优化问题目标函数确定的适应值、个体飞行经验和群体飞行经验为依据，对粒子自身速度和最优位置进行不断地动态调整，直至得到最优解[11]。算法描述如式(11)所示：

(11)

式中：ω是权重因子；C1，C2是学习因子，一般情况下C1=C2=2；r1和r2是[0,1]之间的随机数；k是速度弹性系数，通常取1。为了加快收敛速度，令权重因子ω随算法的迭代线性递减，如式(12)：

(12)

式中：itermax是总迭代次数；iter是当前迭代次数；ωmax、ωmin分别是权重因子的最大值和最小值。选择PSO算法对支持向量机的惩罚因子C和核函数宽度系数γ进行优化，能够使建立的模型具有更高的泛化能力和学习精度。

4　案例分析

实验数据取自美国Case Western Reserve University轴承数据中心，驱动端滚动轴承类型为SKF6205深沟球轴承，在该端安装加速度传感器，以48 kHz为采样频率采集振动信号。轴承故障类型包括内圈故障、外圈故障和滚动体故障3种，均属于人工点蚀故障。选取轴承正常振动数据和不同部位、不同程度时的9种故障振动数据进行故障模型建模。采样时间为1 s，轴承转速为1 750 r/min，几何参数为：滚动体直径8 mm，轴承节径38.5 mm，接触角0°，滚动体数9个[12]。实验使用数据有4种故障类型：正常、内圈点蚀、外圈点蚀、滚动体点蚀；包括3种点蚀故障深度：0.18 mm，0.36 mm，0.53 mm。共计10种类别。由于实验数据限制，每类振动信号均有10组振动数据，各选择8组作为训练集，2组作为测试集，则共有80组训练数据和20组测试数据。

4.1故障特征提取

这里重点选择EEMD分解得到的前3个IMF分量进行故障特征量提取。以训练集中正常类型的第一组振动信号数据为例，原信号及前3个IMF分量的时域波形如图1所示。

对第一个IMF分量进行包络谱分析，确定包络谱上内圈、外圈、滚动体故障特征频率处的幅值，计算幅值比。图3为第一组正常振动信号第一个分量的内禀模态包络谱，标注点的横坐标为外圈故障特征频率。

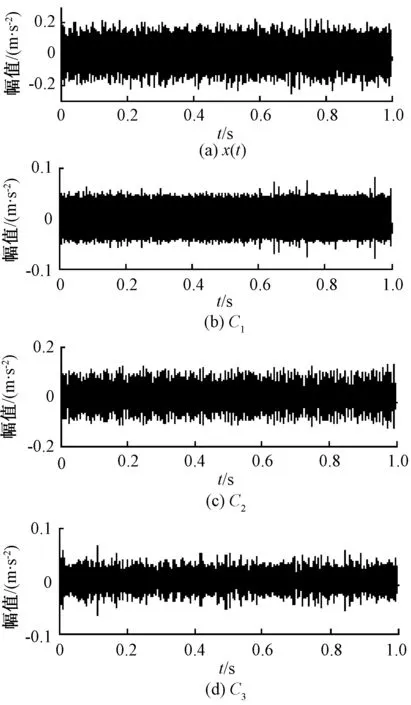
图1　正常信号及前3个IMF分量

图2　归一化的内禀模态能量值

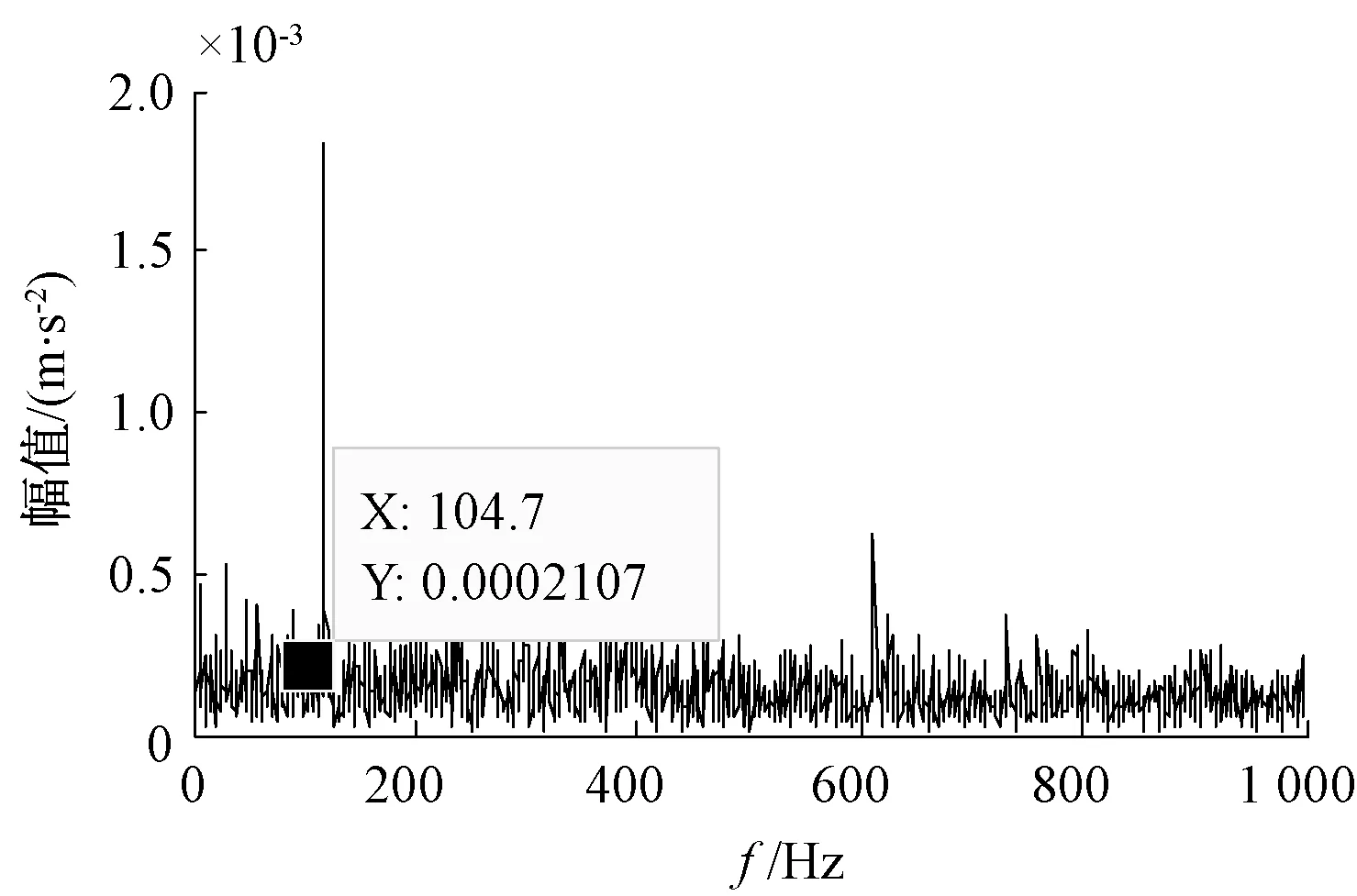
图3　C1的包络谱

经过上述步骤，获得80组训练集特征向量和20组测试集特征向量，部分训练集故障特征向量如表1。以内圈0.18 mm点蚀故障为例，理论上当内圈发生故障时，内禀模态函数的包络谱会在内圈故障特征频率处出现幅值谱峰，幅值比会因此减小，而数据显示内禀模态包络谱的故障特征频率幅值比明显低于正常、外圈、滚动体故障时的数值，与理论相同。

表1　部分训练集故障特征向量

4.2建模与诊断

基于80组训练集数据，利用粒子群算法对支持向量机参数进行寻优。设定粒子群算法的迭代次数为200，种群规模为20，支持向量机参数范围定为：C∈(0.01,103)、γ∈(0.01,10)，在MATLAB中计算出建模最佳参数。对20组测试集进行故障诊断，诊断结果如图4所示。

图4　测试集诊断结果

结果表明，基于粒子群算法的支持向量机对测试集的诊断准确率为95%，也证明了基于EEMD分解得到的IMF分量的内禀模态能量值及内禀模态包络谱特征幅值比能够较大程度地描述信号故障信息，利用EEMD分解方法和基于粒子群的支持向量机结合，可实现对滚动轴承多种不同故障状态的高精度诊断。

5　结论

本文基于EEMD分解方法得到IMF分量，提取内禀模态能量值及内禀模态包络谱特征幅值比等特征参量，构建滚动轴承故障特征向量，在避免EMD模态混叠问题的同时，突出信号故障特征，再基于少量不同故障部位及故障程度的样本，利用基于粒子群的支持向量机实现对测试样本的故障诊断。实验存在不足之处，即样本数量有限制，训练集和测试集样本都较少，但实验结果验证了方法的可行性。振动分析与智能算法结合的方法更适合在计算机上对故障的模式识别和自动化诊断，这也将成为机械故障诊断领域的一种新趋势。

[1]于德介，程军圣，杨宇. 机械故障诊断的Hilbert-Huang变换方法[M]. 北京：科学出版社，2006.

[2]HUANG N E，SHEN Z，LONG S R. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[J]. Proceeding of the Royal Society A Mathematical Physical & Engineering Sciences，1998，454(19)：903 - 995.

[3]WU Z H，HUANG N E. Ensemble empirical mode decomposition：A noise-assisted data analysis method[J]. Advances in Adaption Data Analysis，2009(1)：1-41.

[4]时培明，李庚，韩东颖. 基于改进EMD的旋转机械耦合故障诊断方法研究[J]. 中国机械工程，2013，24(17)：2367-2372.

[5]郑小霞，叶聪杰，符杨. 基于微分改进的EMD滚动轴承局部故障诊断[J]. 南京理工大学学报(自然科学版)，2014，38(1)：59-64.

[6]张璨，文福拴，王建军，等. 联合采用高通低通滤波与Hilbert-黄变换的非线性信号分析[J]. 华北电力大学学报(自然科学版)，2013，40(2)：5-9.

[7]盛敬，魏民祥，刘国满，等. 基于内禀模态特征能量法煤油机爆震特征提取[J]. 仪器仪表学报，2013，34(2)：462-468.

[8]陈盼娣，吕跃刚. 基于EEMD和Hilbert分析的滚动轴承故障诊断方法研究[J]. 电力科学与工程，2013，29(9)：70-73.

[9]张会敏，唐贵基. 基于CEEMD和奇异值差分谱的滚动轴承故障特征提取[J]. 电力科学与工程，2016，32(1)：37-42.

[10]尤晓菲，何青. 基于小波分解和SVM的滚动轴承故障程度研究[J]. 电力科学与工程，2015，31(11)：70-74.

[11]徐晓璐，吴涛，顾宏. 基于IPSO-SVM的地铁车辆牵引控制单元故障诊断[J]. 大连理工大学学报，2015，55(1)：67-72.

[12]周智，朱永生，张优云，等. 基于EEMD和共振解调的滚动轴承自适应故障诊断[J]. 振动与冲击，2013，32(2)：76-80.

Fault Diagnosis of Rolling Bearing Based on EEMD and PSO-SVM

CHEN Yuanyi，SUN Jianping

(School of Control and Computer Engineering, North China Electric Power University, Baoding 071003, China)

In order to realize the fault diagnosis for the rolling bearing with accuracy, based on ensemble empirical mode decomposition and support vector machine optimized by particle swarm optimization, a fault diagnosis method is put forward. EEMD method is used to decompose the vibration signal, while a suitable intrinsic mode function is selected on the basis of experience to calculate fault characteristic parameter, including energy value and feature amplitude ratio of envelope spectrum, to build rolling bearing fault feature vector. Then the particle swarm optimization is used to optimize parameters of support vector machine. Based on a small amount of samples with different fault location and fault degree, samples are trained to build fault model. Finally, test samples are conducted on fault diagnosis and the diagnostic effect of this method was observed. The results show that this method can be used to diagnose a variety of fault conditions, and get better classification accuracy. It is proved that the method which combines vibration analysis and intelligent algorithm can effectively realize the fault diagnosis of rolling bearings.

rolling bearing; ensemble empirical mode decomposition; particle swarm optimization; support vector machine; intrinsic mode function

2016-07-05。

陈园艺(1994-)，女，硕士研究生，主要从事风电机组齿轮箱故障诊断领域的研究，E-mail：1390371570@qq.com。

TH113；TP18

ADOI:10.3969/j.issn.1672-0792.2016.10.008