考虑暂态稳定约束的最大输电能力计算
兰 强,方勇杰
(1.国网西南电力调度控制分中心,四川 成都 610041;2.国网电力科学研究院,江苏 南京 210003)
考虑暂态稳定约束的最大输电能力计算
兰强1,方勇杰2
(1.国网西南电力调度控制分中心,四川 成都610041;2.国网电力科学研究院,江苏 南京210003)
基于最优潮流技术和稳定性量化分析理论的扩展等面积准则(EEAC),提出了在预想故障集下求解互联电力系统暂态稳定约束下的最大输电能力计算方法。基于最优潮流技术建立了最大输电能力的数学模型,采用EEAC量化分析算法获取预想故障集的暂态稳定裕度,针对不安全的预想故障,采用基于安全稳定模式的预防控制技术将非线性的暂态稳定约束转化成临界群机组出力的线性约束,并最终通过内点算法求解。广东电网仿真算例验证了算法的有效性和实用性。
最大输电能力;暂态稳定;最优潮流;扩展等面积准则(EEAC);预防控制
0 引 言
随着特高压交、直流工程的投运,以特高压为骨干网架的坚强智能电网快速发展,跨区输电规模持续增长,跨区输电交易能力大大增强。区域间最大输电能力计算(total transfer capability,TTC)能够充分利用现有电网资源,在确保安全性及可靠性的约束条件下,充分挖掘现有电网输电潜力,最大程度地提高联络线断面的电力传输能力,缓解当今能源供应紧缺状况,满足各区域的用电负荷需求,实现能源资源优化配置。同时,特高压跨省跨区电网互联将出现长距离、高电压、多区域弱联系的交直流混合输电系统,区域间功率交换使电力系统的运行越来越接近其稳定极限。因此,对暂态稳定约束下的最大输电能力的计算展开全面、深入的研究具有重大的社会经济效益。
最大输电能力是系统在没有热过负荷、节点电压越限、电压崩溃或任何如暂态稳定等系统安全限制前提下,互联系统联络线上总的输电能力。TTC是一组可变且相互影响的参数的函数,取决于系统参数、运行工况和运行约束。它不仅要考虑系统正常的运行方式,还要考虑各种故障情况下的静态安全约束和暂态稳定约束。
目前TTC的计算方法主要有基于最优潮流(optimal power flow,OPF)的计算方法、基于连续潮流CPF的计算方法和基于灵敏度的计算方法。其中基于OPF的TTC计算方法可以方便地处理各种系统约束,又可实现对系统资源进行优化调度,兼顾系统运行经济性和安全性,因此在TTC计算方面得到了广泛的应用。文献[1-2]通过对微分方程差分化建立了用静态TTC计算动态TTC的方法。文献[3-4]把基于约束转化技术,将功角稳定约束嵌入最优潮流模型中计算动态TTC。文献[5-6]将TTC模型求解过程分解为暂态稳定最优控制和最优潮流两个子问题。该类方法减轻了动态TTC方法的计算负担,提高了计算效率。
扩展等面积准则(extended equal area criterion,EEAC)[7]建立在时域仿真法的基础上,基于仿真轨迹获得安全稳定裕度、安全稳定模式、控制措施灵敏度等信息,已形成了一整套应用于实际电力系统安全稳定量化评估和优化决策的方法[8]。基于OPF技术建立了暂态稳定约束下的TTC数学模型,模型中全面各种约束条件,包括考虑机组发电功率上下限、支路和断面的热稳定极限、电压约束、等静态运行约束和预想故障集下的暂态稳定约束。在算法求解上,通过稳定性量化分析理论和算法EEAC获得预想故障集下系统的暂态稳定裕度,基于安全稳定模型的预防控制将非线性的暂态稳定约束转化成临界群出力的线性约束,提出了TTC的计算流程,并通过内点优化算法进行求解。
1 基于OPF的TTC数学模型
最大输电能力计算是在特定的电网状态下,根据网络参数、发电机出力变化范围、负荷功率变化范围、各类安全约束和灵敏度,在线计算区域间在某种负荷增长模式下的最大可用输电能力;形成以某一区域间安全条件下最大输电为目标的优化模型,通过快速的优化计算,得到当前网络状态下区域间最大输电能力所对应的发电机出力调整策略。
最优潮流法在求某一断面的TTC时,以输电断面上传输有功功率最大为优化目标。此时将潮流方程作为等式约束,把机组出力约束、节点电压约束、支路和断面的热稳定极限、电压约束等静态运行约束和预想故障集下的暂态稳定约束作为不等式约束,从而把TTC的计算问题转化为一个纯粹的非线性规划的数学问题。
1.1目标函数
TTC的计算问题可以描述为指定联络线组成的输电断面上传输有功功率最大化的优化问题,其目标函数可以表示为
(1)
式中:Pij为线路ij上沿指定方向(送电侧到受电侧)输送的有功潮流;SΩ为断面线路集合。将目标函数取为最大传输容量的负值,将TTC的计算描述为一个含约束的极小化问题求解。
1.2等式约束
系统的潮流方程是优化问题的等式约束,其表达式为
(2)
式中:PGi和QGi分别为节点i发电机有功、无功功率;PLi和QLi分别为节点i有功和无功负荷;Vi和θi分别为节点i的电压幅值和相角;θij=θi-θj;Gij和Bij分别为节点导纳矩阵的实部和虚部元素。
1.3不等式约束
1.3.1静态安全不等式约束
静态不等式约束的表达式为
(3)
式中,SG、SR、SN、SCL,分别表示可调有功发电机集合、可调无功发电机集合、节点集合以及线路集合。
以上不等式约束,分别表示可调发电机有功出力的上、下限约束,可调发电机无功出力的上、下限约束,节点电压幅值的上、下限约束,线路静态运行约束。
1.3.2热稳定约束
热稳定约束是指发生热稳定约束对应的故障集FS(n-1故障)中任意故障的情况下,支路集S(事先定义的容易发生功率越线的支路集合)中的所有支路都满足热稳定约束。其数学表达式为
(4)
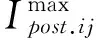
1.3.3暂态稳定约束
暂态稳定约束是指在暂态稳定约束对应的故障集FT中发生任意故障时,系统都不会暂态失稳。扩展等面积准则(EEAC)提供了系统在各故障场景下的暂态功角稳定裕度η,只要预想故障集中所有故障的η>0,则系统暂态稳定,据此可将暂态稳定约束表述为如下不等式约束:
ηk(u,x)≥ε>0k∈FT
(5)式中:u、x分别为系统控制变量和系统状态变量;ηk为预想故障集下故障k的暂态功角稳定裕度,它是关于系统控制变量和状态变量的复杂非线性函数;ε为暂态功角稳定裕度最小值,其ε>0可以保证系统留有一定的稳定裕度;FT为暂态稳定预想故障集。
2 暂态稳定约束实用化
由于TTC的计算需要考虑预想故障集下的暂态稳定约束,使得TTC的求解成为包含了微分和代数方程的函数空间的非线性优化问题,直接求解十分困难。因此,将基于EEAC揭示的暂态稳定机理,通过约束转化技术将非线性的暂态稳定约束转化成临界群机组处理约束,把TTC的计算问题转化为一个纯粹的非线性规划的数学问题。
2.1暂态稳定模式和限制性故障筛选
TTC的计算需要考虑多种可信的预想故障才具有适用价值,但是在大多数预想故障下系统都能维持暂态稳定。如果把所有的预想故障都加入式(5)中同时处理,必然会造成计算量过大,为此需采用适当的故障筛选方法来降低问题规模,使得暂态稳定约束集降阶化、条理化。
EEAC理论从多机系统运动轨迹出发,把系统划分为一对主导互补群{临界群S,余下群A},它们描述了系统的失稳模式。对于具有相同失稳模式的多种故障场景而言,满足最严重故障要求的调度功率完全可以满足该失稳模式下其他故障场景的要求。把相同失稳模式下的最严重故障作为限制性故障,搜索该故障的控制策略,得到的措施能够满足同一失稳模式下所有故障的要求。
综上所述,限制性故障的筛选流程如下:
1)依据EEAC理论对预想故障集进行暂态稳定评估,获取失稳故障;
2)依据失稳故障进行模式分类,对属于同一模式的故障归为同一类;
3)依据稳定裕度辨识各失稳模式中最严重故障,不同模式的最严重故障就构成限制性故障集,并将其作为TTC计算的作用约束。
2.2暂态稳定预防控制
暂态稳定约束式(5)是关于系统控制变量和状态变量的复杂非线性函数,为了使TTC的计算实用化,须将问题加以简化,用限制性故障的实用暂态安全稳定约束代替非线性约束。在研究多机系统的轨迹稳定性时,EEAC指出:在大扰动下系统倾向于以S机群领先于A机群的失稳模式失稳。在临界群S和余下群A之间进行有功调度,减少临界群S机组出力并在余下群A机组中补偿,则有利于系统稳定性。为了量化某一失稳模式下不同机组对稳定性的影响程度,EEAC算法根据两群内机组的能量分布给出了各机组的功角稳定性参与因子,S群机组和A群机组的参与因子分别在[0,1]、[-1,1]区间规格化,参与因子大小反应了机组对系统稳定性的影响。S群机组参与因子越大,减少其出力越有利于稳定该模式,A群机组参与因子越小,增加其出力越有利于稳定该模式。因此,可将两群增减总出力约束取代上述非线性暂态稳定约束,发电机出力调整方向是经模式分析获得的临界机群减出力、剩余机群增出力组合,其增减出力限值来自于预防控制计算。
预防控制策略搜索优化模型的目标函数为
(6)
式中:Ω是可调措施指标集;Cpk(ΔPk)是措施k的调整代价(表达为注入修正量ΔPk的线性函数)。
优化模型中需考虑系统的功率平衡约束和变量限值约束。
预防控制针对失稳的故障模式,综合各个模式的机组参与因子,剔除互斥的机组并排序。按照机组排序结果、候选控制措施的调整限值以及设定的步长形成多个调整方案并分别计算,选择满足所有故障模式且调整量最小的调整方案。
预防控制的计算结果在注入量空间中定义了一个由临界群发电机极限功率表示的暂态稳定域,该稳定域内的运行点满足约束(5),据此可将非线性的暂态稳定约束转化成线性的临界群机组出力约束,转化之后暂态稳定约束可以表示为
Pm≤Pm.OPF-ΔPmm∈Na.c
(7)式中:Pm为失稳模式m下临界群机组有功出力;Pm.OPF为临界群机组在不考虑暂态稳定约束的TTC运行方式下临界群机出力;ΔPm为预防控制计算出的为稳定失稳模式m的临界群机组有功出力调整量。
3 TTC算法
通过暂态稳定约束的实用化,TTC问题已转化成纯粹的非线性规划问题,其计算步骤如下:
1) 静态安全运行约束下的TTC计算。采用现代内点算法求解静态安全运行约束(包括发电机容量约束、节点电压约束、线路热容量约束)下的TTC。
2) 暂态稳定评估。基于EEAC的量化分析算法进行潮流和暂态稳定仿真,获得考察的预想故障集下系统的稳态场景和暂态过程;利用EEAC量化分析理论求取系统在各故障场景中的暂态稳定裕度。若存在故障场景使得系统暂态不安全,则提供失稳模式、机组参与因子,用于暂态稳定预防控制计算。
3) 过载评估。利用过载评估算法进行数据挖掘,求取系统在各故障场景中的故障后设备过载裕度。
支路的过载安全裕度η定义为
(8)
式中:Lrat为监测支路额定值;Lrea监测支路实际值。如果(Lrat>Lrea),则监测元件静态安全;如果(Lrat 4)最优解判断。根据评估结果,若系统在每一故障场景下均暂态和静态安全,则已获得最优解,输出TTC值;否则继续步骤5)。 5) 暂态稳定预防控制。若存在暂态失稳故障,则按照第2节方法筛选出限制性故障,通过暂态预防控制计算出临界群机组的调整量。 6) 过载预防控制。若存在故障后设备过载的故障,则采用潮流灵敏度分析技术计算出每台发电机出力对断面组成元件功率变化的灵敏度,按照灵敏度指标由大到小顺序对机组排序,逐步试探得热稳定控制策略。 7)计及热稳定约束和暂态稳定约束下的TTC计算。根据预防控制措施,修正相关控制变量的约束条件重新计算TTC,转步骤2)。 根据上述步骤,可得到如图1所示的TTC算法流程。 4.1TTC计算结果 以广东电网某实际运行工况断面为测试系统,该系统有110台发电机,716个母线,721条支路,负荷为28 649 MW,其中60%为感应马达模型,16%为恒阻抗模型,24%为恒功率模型。该网内,由“江茂双回+茂阳线+河春线”构成粤西外送断面,江茂双回为500 kV线路,茂阳线和河春线为220 kV线路。粤西外送断面承担着将粤西地区的电力输送到江门电网的任务,本算例将计算在预想故障集下粤西外送断面的最大传输容量。 图1 TTC算法流程 OPF目标函数设置为粤西外送断面线路的传输功率最大;控制变量包括为粤西地区机组、江门地区机组以及全网发电机无功出力;约束条件包括系统运行约束(节点电压约束、机组出力约束、线路电流约束)、N-1故障下的热稳定约束和暂态稳定约束。热稳定约束故障集FS设置为断面相关线路发生开断故障,S为断面相关线路组成集合;暂态稳定约束故障集FT设置为断面相关线路茂名侧线路首端发生三相短路故障,线路0.1 s后切除500 kV线路故障,0.12 s后切除220 kV线路故障。 表1 静态和暂态稳定约束下TTC计算结果 注:茂名厂、湛江厂属粤西地区机组,铜鼓厂、心田厂为江门地区机组粤西外送断面静态TTC为1618.7 MW,暂态稳定约束下TTC为1 410.9 MW 为显示暂态稳定性约束条件对TTC计算结果的影响,这里计算出了只考虑静态运行约束和考虑暂态稳定约束的两种情况下TTC的结果。表1列出了两种情况的计算结果,表2列出了两种情况下预想故障的暂态稳定裕度。 表2 不同运行方式下预想故障暂态安全裕度 从表1和表2所示的TTC计算结果可见,粤西外送断面受制于预想故障集下的暂态稳定约束,使其外送极限传输容量由1 618.7 MW降低为1 410.9 MW。因此,忽略暂态稳定约束不可避免地会导致系统运行风险,只有加入暂态稳定约束的TTC计算才具有实用价值。 基于OPF技术建立了考虑暂态稳定约束的TTC计算模型;限制性故障的筛选技术解决了多个预想故障处理的难题,使得暂态稳定约束集降阶化、条理化;基于EEAC的预防控制技术解决了在TTC中考虑暂态稳定约束的难题,并提出了工程可接受的适用算法,特别有利于TTC在在线计算环境下的工程实施。广东电网仿真算例验证了算法的有效性和实用性。 [1]North American Electric Reliability Council.Available Transfer Capability Definitions and Determination: A Reference Document Prepared by TTC Task Force[R].New Jersey,1996. [2]LA Scala Massimo,Trovato,Antonelli C.On-line Dynamic Preventive Control:An Algorithm for Transient Security Dispatch[J].IEEE Trans on Power Systems,1998,13(2):601-610. [3]袁越,久保川淳司,佐佐木博司.考虑暂态稳定约束的可用传输能力计算[J].电力系统自动化,2004,28(10):34-39. [4]刘明波,夏岩,吴捷.计及暂态稳定约束的可用传输容量计算[J].中国电机工程学报,2003,23(9):28-33. [5]杨新林,孙元章,王海风.考虑暂态稳定约束性约束极限传输容量的计算方法[J].电力系统自动化,2004,28(10):29-33. [6]A.L.Bettiol,L.Wehenkel,M.Pavella. Transient Stability-constrained Maximum Allowable Transfer[J].IEEE Transactions on Power Systems,1999,14(2):654-659. [7]薛禹胜.运动稳定性量化理论:非自治非线性多刚体系统的稳定性分析[M].南京:江苏科学技术出版社,1999:173-194. [8]徐泰山, 刘华伟, 鲍颜红,等.基于静态和暂态安全稳定模式的大电网在线预防控制方法[P].中国:CN200710135089.2,2007-11-8. [9]孙景强,房大中.暂态稳定约束下极限传输能力的计算[J].电力系统自动化,2005,29(8):21-25. [10]Chen L, Tada Y, Okamoto H, et al. Optimal Operation Solution of Power System with Transient Stability Constraints[J].IEEE Transactions on Circuits and Systems,2001, 48(3):327-339. [11]Scalaml,Trovato M,Antonelli C. On-line Dynamic Preventive Control:An Algorithm for Transient Security Dispatch[J].IEEE Trans.on Power Systems,1998,13(2):601-610. [12]Gan De-Qiang, Thomas R J, Zimmerman R D. Stability Constrained Optimal Power Flow[J].IEEE Trans.on Power systems,2000,15(2):535-540. [13]Yue Yuan,Junji Kubokawa,Hiroshi Sasaki.A Solution of Optimal Power Flow with Multicontingency Transient Stability Constraints[J].IEEE Trans.on Power Systems,2003,18(3):1094-1102. [14]孙景强,房大中,锺德成,等.暂态稳定约束下的最优潮流[J].电机工程学报,2005,25(12):12-17. [15]D.Ernst,D.Ruiz-Vega,M.Pavella,et al,A Unified Approach to Transient Stability Contingency Filtering,Ranking and Assessment[J].IEEE Trans.on Power Systems,2001,16(3):435-443. [16]David A K,Lin xu jun.Dynamic Security Enhancement in Power Systems[J].IEEE Trans.on Power Systems,2002,17(2):431-438. [17]Found A A,Tong J.Stability Constrained Optimal Rescheduling of Generation[J].IEEE Trans.on Power Systems,1993,8(8):105-112. [18]薛禹胜.暂态稳定预防控制和紧急控制的协调[J].电力系统自动化,2002,26(4):1-4. [19]鲍颜红,徐泰山,许立雄,等.暂态稳定预防控制及极限功率集群计算[J].电力系统自动化,2010,34(1): 32-35. Based on extended equal area criterion (EEAC) with optimal power flow and the quantitative analysis theory of power system stability, a new method is presented for implementing transient stability constrained total transfer capability (TTC). The mathematic model of TTC is established based on optimal power flow (OPF). According to stability margins calculated by EEAC, the harmful contingencies are identified. Based the preventive control calculation results, the transient stability constraints are converted into inequality constraints of control variables which are incorporated into OPF model. TTC is finally solved by modern interior point method. The effectiveness of the new method is verified by the simulation results using the data of Guangdong power system. total transfer capability; transient stability; optimal power flow; extended equal area criterion (EEAC); preventive control TM744 A 1003-6954(2016)04-0067-06 2016-02-22) 兰强(1985),工程师,主要研究方向为电力系统安全稳定分析与控制; 方勇杰(1964),研究员级高级工程师,主要研究方向为电力系统安全稳定分析与控制。4 仿真算例分析



5 结 语

