12 kV开关柜三相母线短路电动力有限元分析

胡传振，陈志英

(厦门理工学院电气工程与自动化学院，福建 厦门 361024)



12 kV开关柜三相母线短路电动力有限元分析

胡传振，陈志英

(厦门理工学院电气工程与自动化学院，福建 厦门 361024)

以ABB 12 kV开关柜三相平行母线排为对象，利用COMSOL 5.0建立母线排有限元分析模型，计算短路稳态与暂态下母线排所受电动力大小，并且绘制出三相母线所受电动力在x-y平面内的分布和随时间变化的规律.将仿真与经典公式计算结果进行对比，验证了该计算模型的有效性.仿真结果表明：各相所受电动力均是交变的，其频率为电流频率的两倍；暂态下，三相母线中B相所受到电动力最大，为6 989.4 N，为A相或C相所受电动力的1.07倍并且暂态分量存在了0.16 s.仿真结果为12 kV开关柜母线结构优化设计和电动稳定性分析提供参考依据.

开关柜；三相母线；短路；电动力；有限元；COMSOL

发电厂和变电所各类开关柜中广泛地使用母线连接各种电机和电器，传输电流和功率，并通过配电装置分配电能[1].当母线发生短路故障时，短路电流在母线上产生巨大电动力，尤其是在空间狭小的开关柜中，母线排之间距离相对较小，产生的破坏力更大[2-5].这不仅危及母线和开关柜本身运行，而且给整个系统安全稳定带来了隐患[6].为了避免母线导体受到过大电动力而发生形变或损坏，精确计算短路电动力至关重要[7].传统的方法是采用经典公式法计算母线所受电动力大小，经典公式法理论性较强，求解变量较多且计算时间较长，并不能直观地反应电动力在电磁场x-y平面内的分布和随时间的变化规律.这种方法所计算母线电动力与实际母线所受电动力存在偏差，为了得到精确结果，本文采用有限元法(finite element method)计算电动力[8].使用大型有限元分析软件COMSOL Multiphysics对12 kV开关柜母线短路电动力在稳态和暂态下进行精确计算和仿真分析，仿真计算出短路电动力最大值、出现时间以及随时间变化规律，为12 kV开关柜母线的尺寸设计、空间布局提供依据.

1　三相母线有限元物理模型的建立

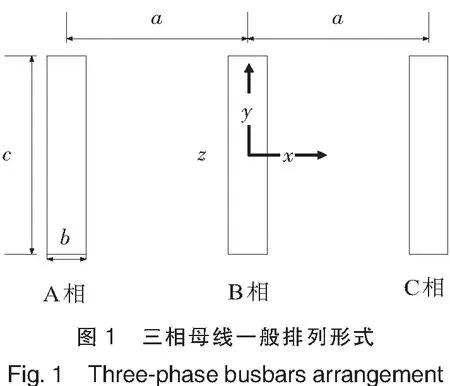
三相矩形母线截面在x-y平面的排列形式如图1所示.表1为ABB 12 kV某型号开关柜母线具体参数，其中短路电流峰值ip为50 kA，a为相邻导体中心距离，b为每相导体宽，c为每相导体高，d为每相导体长，长沿z轴方向，R/L为短路电流非周期分量的衰减系数[9].

表1　12 kV开关柜母线参数

矩形母线通过50 Hz交流电，三相母线发生对称短路时电流为

(1)

式(1)中：ip为短路电流峰值；ψ为初始相位角；φ为电流滞后电压的相位角；式(1)中第一项为电流周期分量，即稳态分量；第二项为电流非周期分量，即暂态分量.

关于模型的几点说明：

1)所建为二维模型，电流密度仅有z轴方向，磁通密度B位于整个x-y平面，又由于对称性，电动力只有x轴方向分量.

2)短路故障为三相对称短路，因为三相对称短路导致电动力最大.

3)母线相间距离远远小于导体长度，这样母线导体可视为无限长.因此仿真计算出结果均为单位长度导体所受电动力，最后再乘以母线实际长度，即得出母线排实际受力.

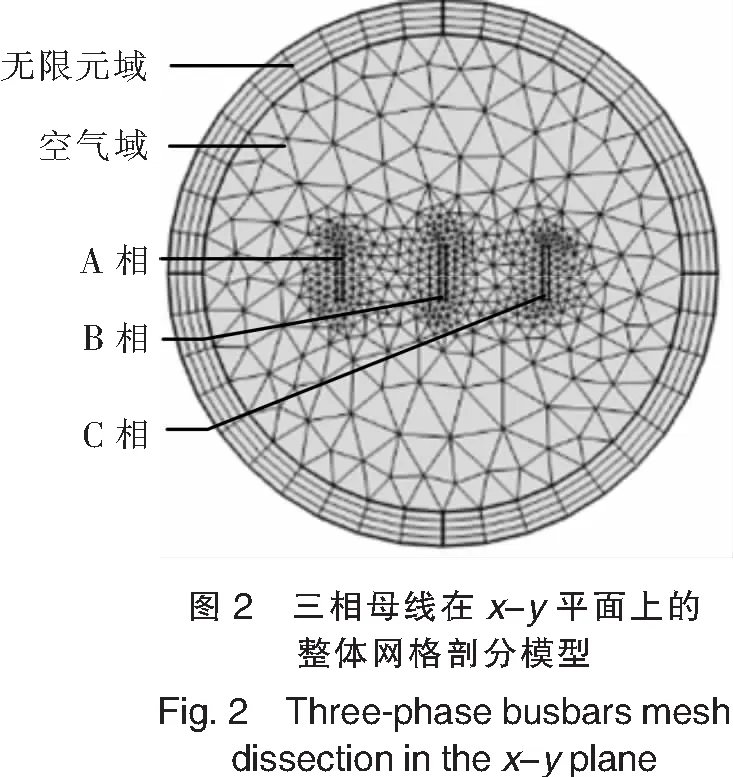
在COMSOL中建立x-y平面模型，剖分网格是一个重要环节，网格划分合理性对整个分析过程及计算结果精确度和正确性有着很大影响[10].将三相母线截面离散化后，得到三相母线在x-y平面上的整体网格剖分模型，如图2所示，母线及其周围剖分密度大，网格较小，远离母线地方网格较大，这样既能达到所要结果精度，又能节约计算资源，缩短运行时间.最外层矩形网格单元组成了无限元域，其作用是将几何模型在z轴方向有效延伸到无限.

2　三相母线短路电动力计算

2.1经典公式计算方法

短路时母线所受电动力取决于母线导体几何排列和外形尺寸，根据文献[9]中所推导经典公式计算如下.

单相交流稳态下最大电动力为

(2)

式(2)中：k1,2为回路系数；kc为形状系数；F0为单相交流稳态下最大电动力；u0为真空磁导率[9].

三相交流稳态下最大电动力为

(3)

(4)

三相交流暂态下最大电动力为

(5)

(6)

式(3)～(6)中：Fma、Fmb、Fmc分别为A、B、C三相所受最大电动力.

2.2有限元计算方法

母线截面位于x-y的平面内，矢量磁位Az满足二维电磁场微分方程

即

(7)

式(7)中：u为介质磁导率；ω为转动角速度；σ为电荷面密度；Jsz为源电流密度；Jz为z方向的全电流密度[11].

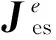
(8)

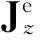
(9)

式(9)中，对任一导体截面积的积分就是通过这一导体的全电流.

为了计算作用在每个导体上的电动力，必须求得单元e内的磁通密度.磁通密度可由矢量磁位的分布按下面的关系求得.

(10)

(11)

设体积元dv内全电流密度J作用在dv上的力dF为

(12)

根据假设[3]，电动力只有x方向分量，故i相导体单元e所受到电动力为

(13)

式(13)中

(14)

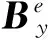
(15)

(16)

将式(15-16)代入式(14)，得到单元e所受x方向力的时间函数为

(17)

所有单元所受x方向力之和即为导体i所受电动力[12]，即

因此，单位长度导体所受到电动力为

(18)

3　仿真结果与分析

3.1稳态和暂态下最大电动力对比

当ψ-φ=0°时，有限元法(FEM)与经典公式(3)(4)计算所得稳态下，最大电动力值如表2所示.从表2中可以看出，两种方法计算结果比较接近，有限元法与经典公式法的结果误差不超过2%，经典公式法比有限元法结果小了7～23N，两种方法电动力最大值均为B相.计算机仿真结果也验证了文献[9]中的结论：B相受到最大电动力为A相所受到最大电动力的1.07倍.

表2　稳态下各相最大电动力值对比

表3所示为12 kV开关柜三相母线暂态下有限元法FEM与经典公式(5)(6)计算所得电动力最大值.表3中显示两种方法计算结果误差较小，均不超过1.5%，其中公式法计算得到B相所受的电动力比有限元法小了73 N，所以在设计母线时，应当参考有限元法的计算结果.

表3　暂态下各相最大电动力值对比

表4所示为三相母线排暂态下所受电动力最大值，其中ψ-φ每隔15°取一次.表4数据表明，当ψ-φ=75°或165°时，B相暂态下所受电动力达到最大值6 989.4 N；当ψ-φ=75°时，A相暂态下所受电动力达到最大值6 539.8 N；当ψ-φ=165°时，C相暂态下所受电动力达到了最大值6 551.2 N.

表4　三相母线排暂态下所受电动力最大值

3.2计算机仿真图像分析

当ψ-φ=75°且t=0.009 85 s时，A相暂态下所受电动力达到最大值，从图3(a)也可以看出A相和B相周围磁通密度最大，A相与B相母线导体Maxwell表面应力张量也达到最大值.图3(b)为ψ-φ=165°且t=0.009 8 s时，三相母线暂态下Maxwell表面应力张量，此时C相达到最大值.

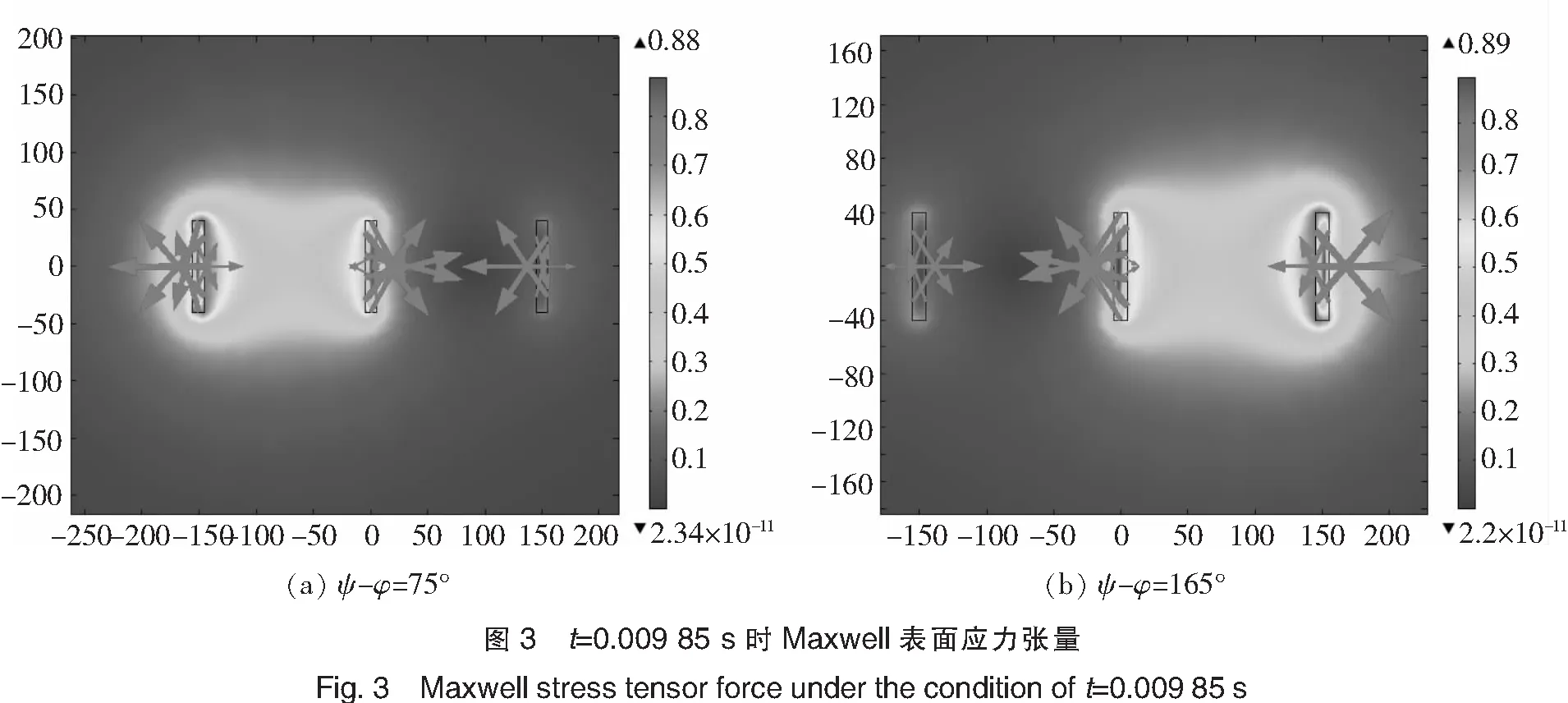
图4为ψ-φ=75°时，A相与B相暂态电动力大小随时间变化曲线.AB两相所受电动力均是交变的，其频率为电流频率的两倍，即100 Hz.图4(a)中，A相电动力最大值出现在工频第一个周期内，在前8个周期内暂态分量从最大值逐渐衰减趋向于0，在第8个周期后变成稳定变化的正弦波周期分量.图4(b)中，随着时间增加，电动力最大值包络线一开始呈指数下降，当t>0.16 s后，电动力最大值包络线趋于平稳.

3　结论

基于电磁学理论建立12 kV开关柜三相母线电磁场有限元模型，使用有限元法和经典公式法对母线短路电动力在稳态和暂态下进行计算对比和仿真分析，绘制出三相母线所受电动力在x-y平面内的分布和随时间变化的规律，并得出以下4点结论.

1)各相所受电动力均是交变的，其频率为电流频率的两倍，即100 Hz.

2)暂态下，三相母线中B相所受到电动力最大，为6 989.4 N，为A相或C相所受电动力的1.07倍.

3)12 kV开关柜三相母线暂态所受电动力最大值出现在第一个周期内，暂态分量存在了0.16 s.仿真计算出短路电动力最大值、出现时间以及随时间变化规律，为12 kV开关柜母线的材料选取、尺寸设计、空间布局提供了依据.

4)经典公式法计算得到电动力比有限元法小，如果采用公式法所设计出的母线可能无法满足稳定性要求，最好采用有限元法.

[1]吴励坚.大电流母线的理论基础与设计[M].北京:水利水电出版社,1985:1.

[2]程鹏,杨帆,范丰英,等.基于热-流耦合场的大电流母排热场计算及影响因素分析[J].低压电器,2013(5):14-19.

[3]李洪杰,王颖,冯允平,等.短外壳封闭母线电动力的计算[J].高压电器,1997(5):31-33,56.

[4]舒乃秋,关向雨,康兵,等.基于场路耦合有限元的三相共箱气体绝缘母线暂态电动力分析[J].电网技术,2015,39(5):1 456-1 462.

[5]胡冰,张晓峰.用有限元法计算三相矩形母线的短路电动力[J].电气应用,2005(2):83-85.

[6]骆明峰,陈为,刘明明,等.配电开关柜短路燃弧故障检测与保护装置[J].电器与能效管理技术,2015(7):21-24.

[7]廖宝文,曾奕,杨皓宇.有限元法计算三相管型母线的短路电动力[J].电气技术,2013(2):12-13,18.

[8]马慧,王刚.COMSOL Multiphysics基本操作指南和常见问题解答[M].北京:人民交通出版社,2009：143-144.

[9]孙鹏,马少华.电器学[M].北京:科学出版社,2012:40-55.

[10]TRIANTAFYLLIDIS D G，DOKOPOULOS P S，LABRIDIS D P.Parametric short-circuit force analysis of three-phase busbars-a fully automated finite element approach[J].IEEE Transactions on Power Delivery,2003(2):532-533.

[11]WEISS J，CSENDES Z.A one-Step finite element method for multiconductor skin effect problems[J].IEEE Transactions on Power Apparatus and Systems,1982,101(10):3 796-3 803.

[12]LABRIDIS D P，DOKOPOULOS P S.Electromagnetic forces in three-phase rigid busbars with rectangular cross-sections[J].IEEE Transactions on Power Delivery,1996,11(2):793-800.

(责任编辑李宁)

A Finite Element Analysis of Short-Circuit Force onThree-Phase Busbars in 12 kV Switch Cubicle

HU Chuanzhen，CHEN Zhiying

(School of Electrical Engineering & Automation，Xiamen University of Technology，Xiamen 361024，China)

A model of three phase parallel busbars in 12kV switch cubicle of ABB making was established by COMSOL finite element simulation software in order to calculate and simulate the results of three-phase busbars under the condition of steady state and transient state.The distribution of electromagnetic force in x-y plane was mapped as well as its pattern of electromagnetic force over time，and the results of the finite element model with those from classical formula method was compared to verify the validity of the calculation model.The simulation results show that electromagnetic force of each phase is alternating and its frequency is twice that of current frequency.The electromagnetic force of B phase is the largest under the condition of transient state and its value is 6 989.4 N，1.07 times that of A and C phase.Meanwhile，the transient component existed for 0.16 second.The calculation model and the analysis results can be helpful for configuration optimal design and short circuit fault monitoring of three phase busbars in 12 kV switch cubicle.

switchgear；three phase busbars；short circuit；electromagnetic force；finite element；COMSOL

2015-12-03

2016-04-20

福建省教育厅科技项目(JK2013036);厦门理工学院教改项目(JGY201407)

胡传振(1991- )，男，硕士研究生，研究方向为电器智能化技术及应用.通讯作者：陈志英(1978-)，女，副教授，硕士，研究方向为智能电器及其在线监测技术.E-mail：chzy207@163.com

TM591.2

A

1673-4432(2016)03-0034-06