高渗透率下分布式发电对大电网稳定性的影响*

张继元，黄 磊，舒 杰，王 浩，丁建宁

（1. 中国科学院广州能源研究所，广州 510640；2. 中国科学院可再生能源重点实验室，广州 510640；3. 广东省新能源和可再生能源研究开发与应用重点实验室，广州 510640；4. 中国科学院大学，北京 100049；5. 江苏省光伏科学与工程协同创新中心，江苏 常州 213164）

高渗透率下分布式发电对大电网稳定性的影响*

张继元1，2，3，4，黄 磊1，2，3，4，舒 杰1，2，3†，王 浩1，2，3，丁建宁5

（1. 中国科学院广州能源研究所，广州 510640；2. 中国科学院可再生能源重点实验室，广州 510640；3. 广东省新能源和可再生能源研究开发与应用重点实验室，广州 510640；4. 中国科学院大学，北京 100049；5. 江苏省光伏科学与工程协同创新中心，江苏 常州 213164）

为了研究高渗透率下分布式发电对大电网稳定性的影响，针对不同类型的分布式微源特性，提出了相应的并网控制策略，在此基础上建立逆变型分布式电源发电机的动态模型。通过理论分析和仿真，重点研究了分布式发电并网在不同渗透率下对电网静态电压的影响，分析了发电机转速及频率的动态特性，并探讨了不同控制策略的分布式微源在故障期间对电力系统的影响。仿真分析结果表明：微电网能够对大电网提供电压支撑，但渗透率过大会对电网稳定运行产生不利影响；采用电压源型控制策略的分布式微源，能够对故障后电网电压、频率的恢复起到积极作用。

分布式发电；高渗透率；控制策略；静态电压；动态特性

0 引 言

传统电力系统多以化石能源作为一次能源，由于大规模开采使用，造成了能源枯竭、环境污染等问题，严重影响当今社会的发展和进步［1］。基于分布式电源（distributed generation，DG）组建的微电网，为可再生能源（如太阳能、风能、潮汐能及地热能等）的综合利用提供了有效途径［2］。微电网不仅供电灵活、安全可靠，还能够削峰填谷、降低网损，实现绿色、环保的低碳电网，将是解决能源与环境危机的重要途径［3-5］。微电网容量的快速增长以及分布式微源所占比重的不断提高，对大电网的稳定运行产生一定影响。因此，针对高渗透率下分布式发电接入大电网，对电网运行的暂稳态影响进行相关技术研究，将具有重要的理论意义和实用价值。

微电网能够将多种可再生能源有效组织并合理利用起来，但是由于分布式电源多采用基于电力电子的控制技术，导致系统区别于传统电网，具有弱惯性、高抗性以及电气特性各异等特征，使得以分布式发电为基础的微电网构成复杂的供电网络，其运行特性相对传统大电网存在着并网运行、电网故障时孤岛运行、恢复并网等多种状态。处于并网运行情况下的微电网，能够接受上层调度，有效的调节电网的功率平衡，实现微电网的优化调度与经济运行。在电力系统发生电压跌落或故障的情况下，微电网根据孤岛检测以及控制策略，提供电压支撑实现低电压穿越，或者无缝切换至孤岛模式，配合当地供电网络，保障和支撑微电网内部的关键负荷，对于提高供电安全稳定性具有积极作用。

随着大规模分布式电源并网发电接入电网后，将极大地影响整个配电系统，太阳能及风能的功率受外界环境影响较大，可能造成配电系统中电压的波动和闪变，同时大规模的电力电子装置并网将会造成电力谐波污染［6-8］，同时原有的配电系统将作为有源网络进行规划，而系统潮流以及电压分布也将随之变化，尤其是电压的上升越限［9］。高渗透率的分布式发电接入必将对大电网的电压频率和功角稳定性产生重大影响，给大电网的稳定性、调度运行和控制保护策略等方面带来新的问题和挑战［10］，因此有必要研究高渗透率下分布式发电对大电网稳定性的影响、内在机理，以及提高稳定性的策略，为电网的安全运行和微电网规划建设提供理论指导，同时为制订相关大规模分布式发电接入大电网的技术标准和运行规范提供实验依据。

1 分布式微源建模

微电网将多种分布式及常规能源组合，如太阳能、风能、微型燃气轮机发电等，但分布式发电具有随机性和功率波动等特性。因此，需针对微电源进行建模和分析，对其运行特性和控制方法进行研究，以满足微电网强鲁棒性和快速调节的要求。

1.1 光伏发电系统

光伏电池属于半导体光电元器件，其典型的数学模型如下图1所示，由等效电流源、并联二极管以及串、并联电阻组成，其工作特性可通过此等效电路进行描述［11］。

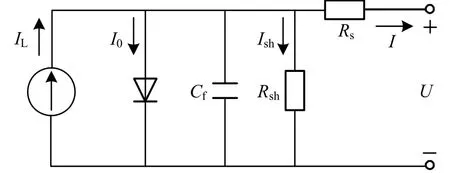
图1 光伏电池模型Fig. 1 Photovoltaic cell model

光伏电池输出电流和电压的非线性I-U特性关系如下式（1）所示。

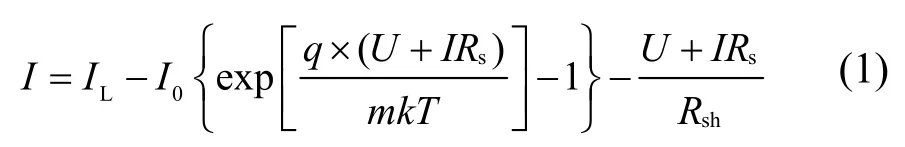
式中：IL为光伏电池短路电流；I0为二极管反向饱和电流，通常取10-4A；q为电子电量常数，1.6×10-19C；m为曲线拟合参数，无量纲，取值范围为1 ≤ m ≤ 2；k为波耳兹曼常数，1.38×10-23J/K；T为光伏电池温度；Rs、Rsh分别为光伏电池串、并联等效电阻，Rsh通常大于 1 kΩ；I、U分别为光伏电池输出电流、电压。

光伏电池的输出特性如图2所示。光伏阵列在特定环境下其P-U特性曲线呈近似抛物线形状，因而存在唯一与其工作电压对应的最大功率点。由此，调节光伏逆变器的输入电压达到特性曲线中对应的最大功率点位置时，即可实现对光伏的最大功率点跟踪（maximum power point tracking，MPPT）。

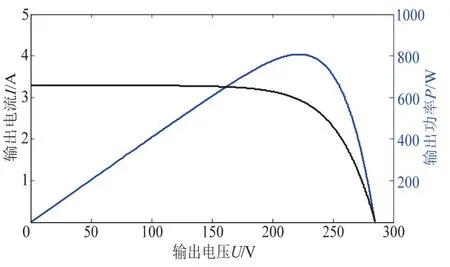
图2 光伏输出特性Fig. 2 Photovoltaic characteristic

1.2 风力发电系统

风力发电系统通常是由扇叶、发电机、整流器和逆变器组成。当气流流过扇叶时，产生与气流流动方向垂直的转矩带动发电机运转，将风能转化为电能［12］。

由空气动力学原理得风力发电系统的输出功率如式（2）所示。

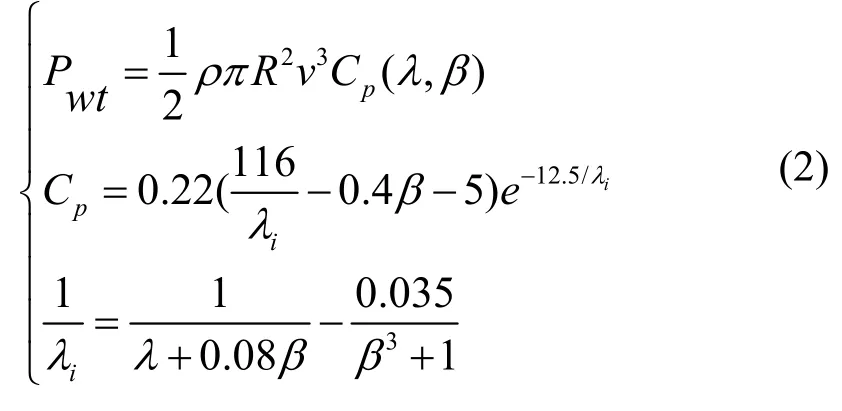
式中：ρ为空气密度，kg/m3；R为扇叶转动半径，m；v为风速，m/s；Cp为风能利用系数，与尖速比λ和桨距角β的相关。在风速和密度不变的条件下，风力系统的输出功率与Cp成正比关系。

随着风机转速不同，风力发电系统输出的功率也不同，但是存在最大输出功率点。不同风速下的功率特性曲线如图3所示，将输出功率曲线簇中的最大点连接起来得到最大功率曲线。

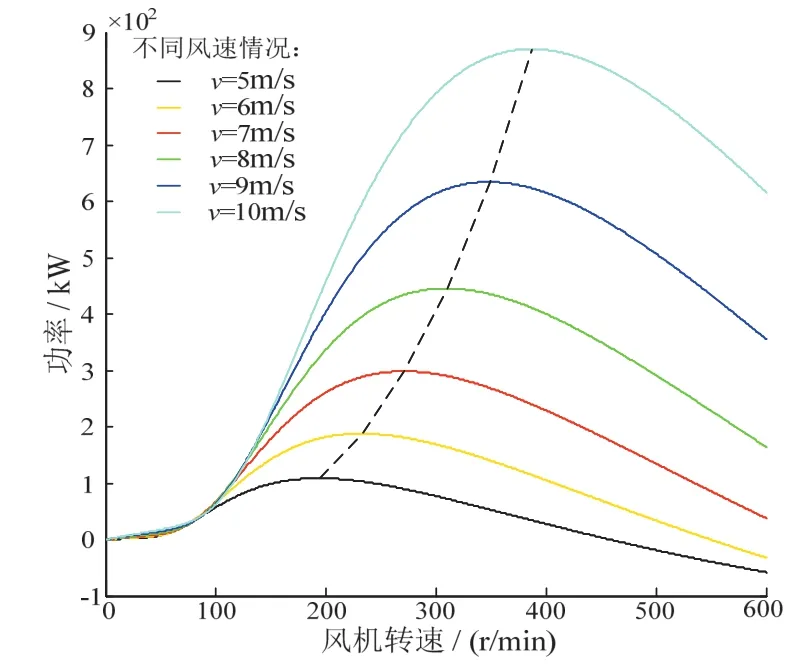
图3 风力系统功率特性曲线Fig. 3 Wind power system characteristic curve

1.3 微型燃气轮机

微型燃气轮机发电系统由燃气轮机、永磁发电机、整流器、逆变器和 LC滤波器组成，采用单轴结构，具有效率高、紧凑可靠的优点［13］。系统结构如图4所示。系统以Rowen所提单轴单循环重负荷燃气轮机模型为基础进行建模［14］，其中控制系统包括转速、温度、燃料和加速度控制模块。控制转速使得在特定负荷下维持转速基本不变；温度控制保证燃气轮机温度在设定的最大值下安全工作；燃料控制以确保足够的燃料流量；加速度控制限制转速变化率过高。燃气轮机带动发电机转动，所产生的交流电经过整流成直流电后，经由并网逆变器产生工频交流电送入大电网［15-16］，为符合微电网运行特性，常采用功率控制（PQ控制）或V/f控制。

燃气轮机的温度函数（f1）和转矩输出函数（f2）分别为：

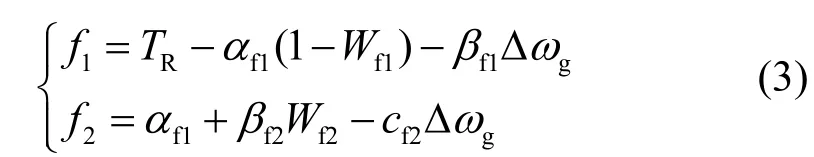
式中：TR为燃气轮机额定温度，视燃气轮机的类型而定；αf1、βf1、αf2、βf2、cf2为系统给定常数；Δωg为转子角速度偏差。

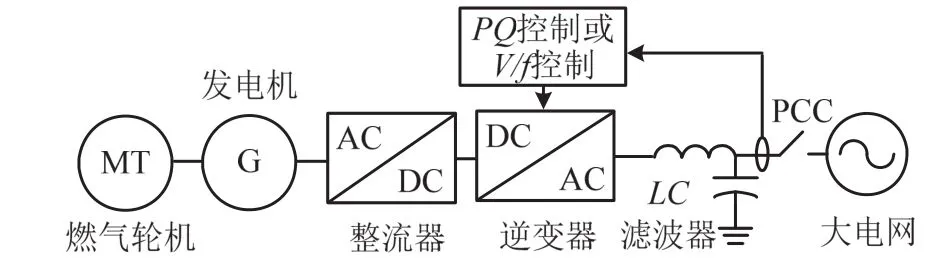
图4 微型燃气轮机发电系统结构Fig. 4 Micro gas turbine power generation system structure

2 微源并网控制策略

微电网中的分布式发电作为受控电源，通过并网逆变器不同策略控制为电压或电流源，与大电网进行交互。典型的并网逆变型拓扑结构如图5所示，采用三相全桥结构，逆变器的开关视为理想开关，基于空间矢量脉宽调制（space vector pulse width modulation，SVPWM）策略运行。

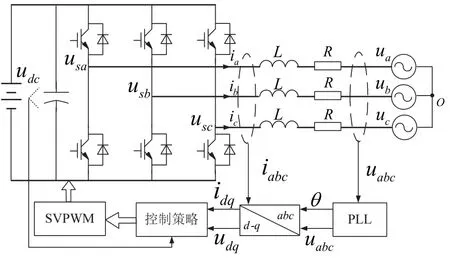
图5 并网逆变器拓扑结构Fig. 5 The topology of grid-connected inverter

根据上图可得到，以流入电网电流方向为正，得到三相静止坐标系下的逆变电压表达式：

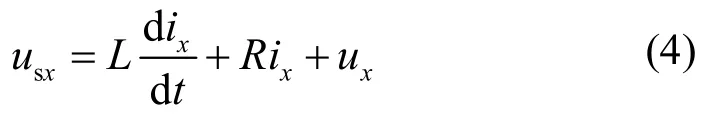
式中，x取三相ABC，由于电网交流变量的时变性，给控制系统的设计带来很大困难。因此，需将数学模型中三相静止坐标系转换成以电网基波频率同步旋转的两相d-q坐标系，通过PARK变换使ABC坐标系下的交流量变换为两相旋转坐标系 d-q轴中的直流分量。

PARK变换矩阵公式：

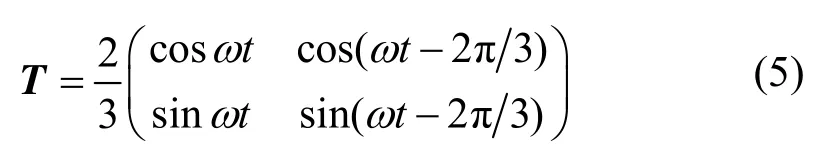
将公式（5）代入公式（4）中，可得到逆变电压在d-q坐标系下的直流分量表达式：

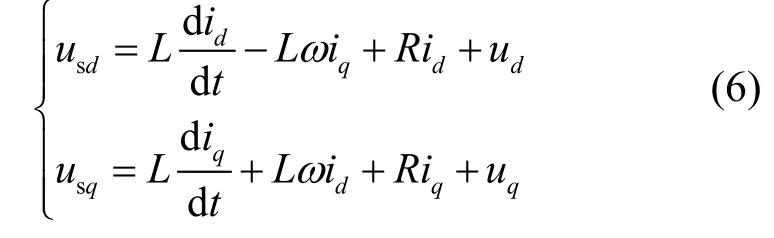
式中，usd、usq分别为逆变输出电压d轴、q轴分量，id、iq为系统输出电流d轴、q轴分量，ud、uq为电网直流分量。由上式可知，系统除受电网扰动影响，还受 id和 iq的耦合影响。根据文献［17］对其进行解耦控制，此时电流控制采用PI控制，实现d-q轴电流的无静差调节。同时在电流参考值前添加两个PI控制器，实现功率 PQ控制策略，这样可通过控制电流分量直接调整相应的功率，PQ控制策略流程图如图6所示。最终计算得出逆变电压usd、usq，将其送入控制器产生脉冲信号，驱动 IGBT从而发出指定电压波形。

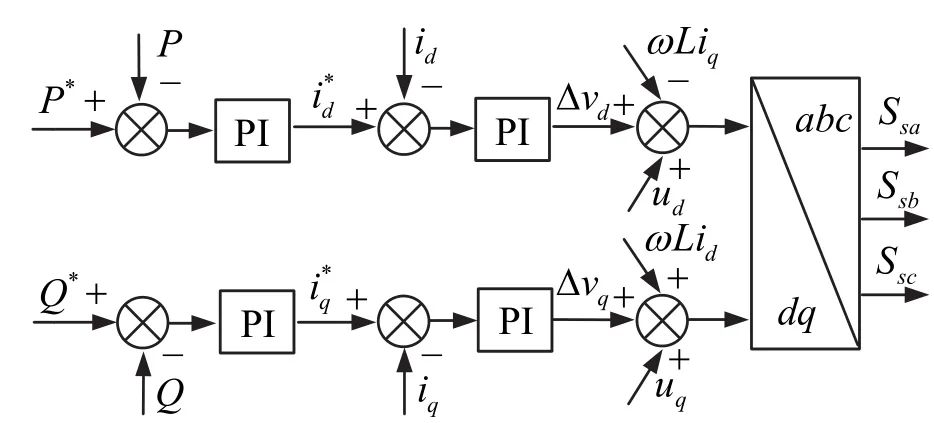
图6 PQ控制策略流程图Fig. 6 Diagram of the PQ control strategy

上述 PQ控制稳定运行的重要前提是，电力系统具有刚性的稳定电压，其电压频率稳定，拥有固定的电气时钟坐标轴，使得 PQ控制能够按照指令输出额定功率。

DG系统不仅具有PQ控制，而采用具有V/f控制策略的分布式发电单元，还可辅助稳定支撑系统运行，能够实现如频率调节、电压控制等功能，帮助建立稳定的系统电压，与采用 PQ控制的分布电源协同组成微电网系统。V/f控制方程如式（7）所示，模式中依据所承担的负荷特性以及预期所要求的V/f频率电压控制效果，需要整定不同的下垂控制系数。

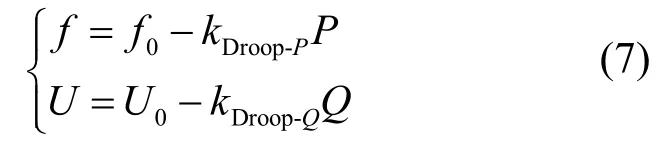
式中，f0、U0分别为空载输出的额定频率与电压幅值，kDroop-P、kDroop-Q为下垂系数。由f、U合成输出指令参考值。考虑到对功率分配精度的影响，下垂系数的选取如下式（8）所示［18-19］：

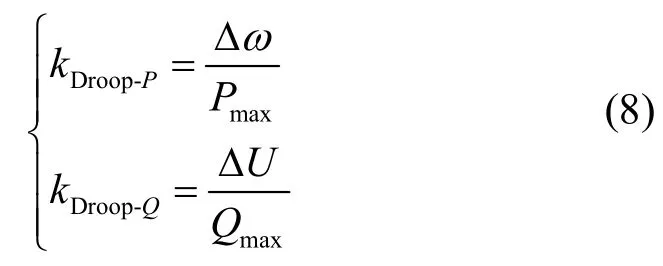
其中，Δω、ΔU分别为角频率和电压幅值偏差最大值，Pmax、Qmax分别为发电系统自身输出最大有功、无功功率。得到输出指令参考值后送入V/f控制，再经过电压外环和电流内环控制，从而精确快速的控制系统电压和频率。

3 分布式发电对电网稳定性的影响

微电网将大规模分布式发电整合后，作为相对于大电网的单一受控源，通过公共连接点（point of common coupling，PCC）实现并网与孤岛运行。目前文献多将微电网作为电流源型并网，系统在具有弱惯性条件下考察不同渗透率对系统稳定性影响，目前的研究缺乏对系统的精确建模，并且仍处于探索阶段。

本文研究探讨分布式发电并网对电网稳定性的影响，主要针对高渗透率下微电网接入对系统的静态电压稳定性和动态特性的影响进行分析。电力系统在不同渗透率的并网情况下能否保持暂态稳定，是电网安全可靠运行的必要前提。而随着大规模分布式发电通过微电网集中接入大电网后，由于微电网内部配置众多分布式电源，使得系统衍生了诸如高电抗、弱惯性等电力电子装置具有的特性，在与传统电网并网运行条件下，尤其是高渗透率下接入系统，势必会对大电网的稳定性产生一定影响。因此，有必要对微电网接入大电网后系统稳定及运行影响进行研究。

目前电力系统稳定性模型通常采用节点测试系统［20-21］，本文对其优化改进，以反映电力电子装置在微电网中的特性，采用图7中所示的微电网系统结构图，研究微电网对电力系统稳定性的影响。

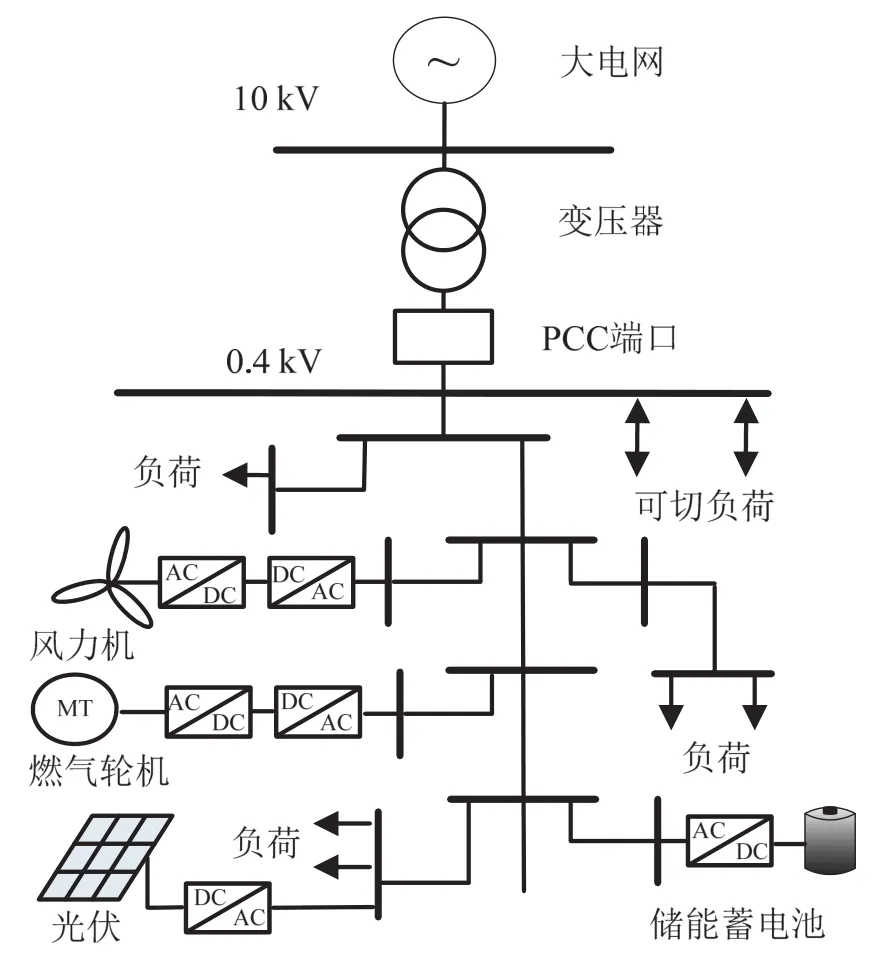
图7 微电网系统结构Fig. 7 Structure of micro-grid system

为定量研究不同渗透率下，微电网对大电网的影响，将渗透率λ定义为分布式发电（或微电网）与大电网交换功率占电力系统总功率的比率，即：

式中：Pm代表分布式发电（或微电网）并网功率，其数值可由微电网中分布式发电总功率PDG与微电网内部总负荷量Pload运算得到；PT代表电力系统总功率；Pi是微电网中第i台分布式微源发电功率；n是分布式微源总数。

由上述可知，当微电网内部分布式微源、负荷发生变化时，微电网渗透率λ也随之改变，通常渗透率λ≥10%即被认为是高渗透率，分布式发电与负荷功率的改变将与电力系统中的主同步发电机互相影响，使系统特性发生变化。用渗透率表征微电网与电网间的功率交换比率，对研究不同容量等级的微电网与电力系统的作用机理有重要意义。

3.1 静态电压稳定性

研究静态电压稳定性，是为了分析并网连接点PCC处的母线电压在不同渗透率情况下的变化趋势。图8所示为以λ=0时作为参考基准，在不同渗透率下的PCC电压曲线。

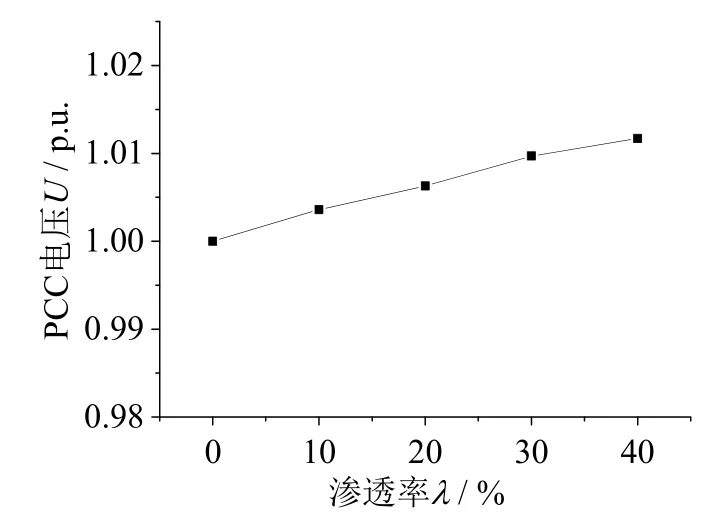
图8 不同渗透率下PCC电压变化Fig. 8 PCC voltage under different penetration

由上图可知，在分布式发电并网情况下，随着渗透率的不断增大（即微电网注入大电网的功率不断增大），系统在稳定状态情况下测定 PCC处电压也相应增大，说明在电力系统中，微电网向大电网注入的功率对电网电压起到了支撑作用。

电压稳定性的定义：在正常运行情况下或遭受扰动后，系统电压能够在允许范围内维持运行。通常电力系统的不稳定包括电压、频率的波动，是由于系统不能满足有功、无功功率的需求［22］。本文在研究不同渗透率下动态特性的同时，将研究不同控制策略的分布式微源对系统电压的影响。

3.2 动态特性分析

对系统的动态特性进行分析，针对电力系统在故障前后并网点PCC处的电压、频率变化进行检测，由此得出在不同渗透率情况下，微电网在故障期间及故障后对电网电压及系统稳定性的影响，并分析导致系统失稳的潜在因素。

3.2.1 动态稳定性分析

由于逆变型分布式发电在微电网应用中较为常见，因此选用逆变型DG发电机作为研究对象，通过变压器接入大电网，研究其对电力系统稳定性的影响。

通过调节DG的输出功率（PQ控制），使逆变型DG在λ=0、20%、40%三种渗透率下运行。为研究动态特性，设置电力系统的输电线路发生三相短路故障，并在发生故障100 ms后，通过跳开故障线路解除故障。在故障期间，逆变型DG发电系统和大电网保持连接。

图9是在三种不同渗透率下，系统发生短路故障期间，逆变型DG发电机的转速特性曲线。由图中可以看出，系统在故障清除恢复稳定运行时，随着渗透率的增加，发电机的转速偏差峰值也随之增大，系统自愈性降低。结合之前的分析可知，渗透率的增加能够为大电网快速恢复提供电压支撑，但同时系统振荡加剧，过高的渗透率可能会引起系统的崩溃。

3.2.2 动态频率分析

图10所示为发生故障期间，DG发电机输出频率的变化曲线。当系统运行在1 s处发生故障，并在100 ms之后清除故障，系统频率经历了不同程度的震荡并最终趋于稳定。大电网以额定频率50 Hz运转，当微电网渗透率由0增大至40%时，频率曲线振荡加剧，恢复至参考标幺值的过渡时间增长。在电力系统发生短路故障到恢复至正常范围的过渡时间内，由于微电网内部引入的电力电子装置，也会对电力系统造成高次谐波干扰，可导致系统频率的小幅度震荡。

3.2.3 不同控制策略特性分析

分布式微源采用不同的控制策略，导致其输出特性相异。为研究控制策略对系统电压的影响，检测在渗透率λ=20%情况下，DG采用V/f控制、PQ控制以及电流控制策略下的转速曲线，如图 11所示。由图可以看出：采用V/f控制策略下的转速偏差最小，振荡周期短以及最快恢复至稳定运行状态。PQ控制以及电流控制在上面的分析中可以看到，其控制本质相似，而V/f控制是通过控制电压的幅值与频率，使系统作为电压源形式与大电网并网运行，当电网故障清除后，能够为大电网的恢复提供功率支撑。

图12是在故障期间不同控制策略下PCC点的电压曲线。从图中可以看到，以故障前的稳态电压为标幺值，故障发生后电压降落曲线一致，在故障清除后，采用V/f控制策略的系统，能够对系统提供电压、频率的支撑，使得电压能够快速恢复至标幺值并稳定运行。

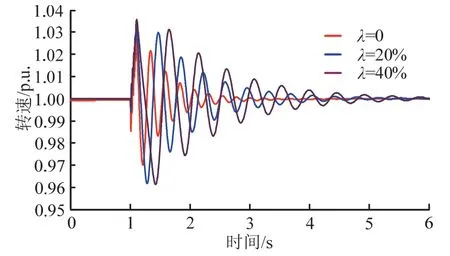
图9 故障期间转速曲线Fig. 9 Speed curve under different penetration during the fault

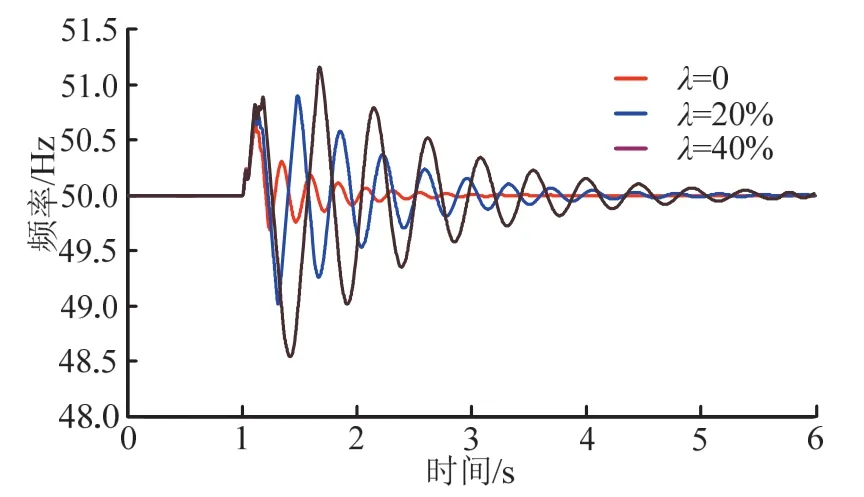
图10 故障期间频率曲线Fig. 10 Frequency curve under different penetration during the fault

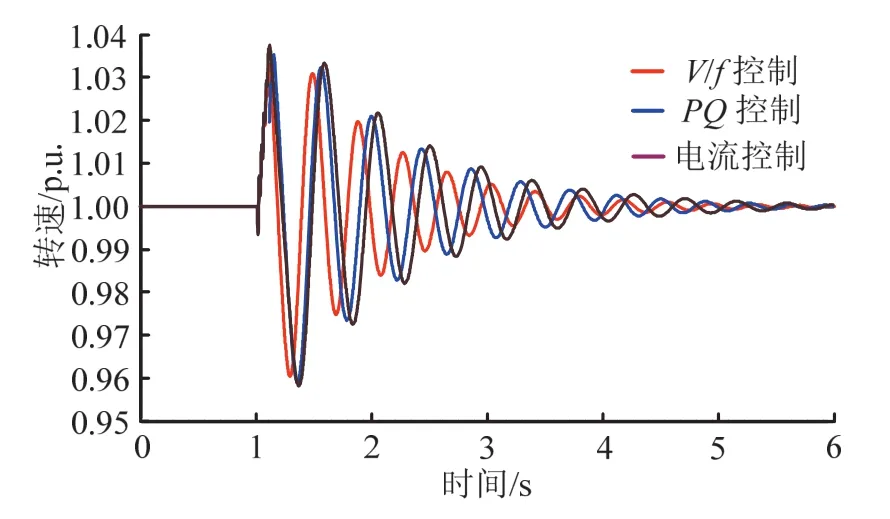
图11 不同控制策略在故障期间转速曲线Fig. 11 Speed curve under different control strategy during the fault

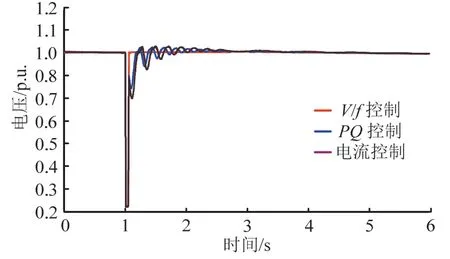
图12 不同控制策略在故障期间电压曲线Fig. 12 PCC voltage curve under different control strategy during the fault

4 结 论

为了研究高渗透率下分布式发电接入对大电网稳定性的影响，对不同类型的分布式电源特性展开研究，建立微电网中光伏发电系统、风力发电系统、燃气轮机等分布式电源模型，同时研究设计了应用于微电网的接口变换器，并提出相应的控制策略。在此基础上建立DG发电机的动态模型，通过仿真可知在不同渗透率下微电网对大电网的电压和频率的影响具有较大差异。微电网能够对电力系统的电压提供一定的支撑，但渗透率过大会导致发电机转速和频率的振荡，影响电网的稳定运行。而采用电压源型控制策略的分布式微源，能够对故障后大电网电压、频率的恢复起到积极作用，改善电网的动态特性。

［1］ 袁越，曹阳，傅质馨，等. 微电网的节能减排效益评估及其运行优化［J］. 电网技术，2012，36（8）: 12-18.

［2］ 杨新法，苏剑，吕志鹏，等. 微电网技术综述［J］. 中国电机工程学报，2014，34（1）: 57-70. DOI: 10.13334/ j.0258-8013.pcsee.2014.01.007.

［3］ 徐敏，阮新波，刘福鑫，等. 氢光联合供电系统的能量管理［J］. 电工技术学报，2010，25（10）: 166-175. DOI: 10.3969/j.issn.1000-6753.2010.10.025.

［4］ 张国驹，唐西胜，齐智平. 平抑间歇式电源功率波动的混合储能系统设计［J］. 电力系统自动化，2011，35（20）: 24-28，93.

［5］ KHANH L N，SEO J J，KIM Y S，et al. Powermanagement strategies for a grid-connected PV-FC hybrid system［J］. IEEE transactions on power delivery，2010，25（3）: 1874-1882. DOI: 10.1109/TPWRD.2010. 2047735.

［6］ 陈杨刚，杨奇逊，张涛，等. 微网中双向 DC-AC变流器的性能优化控制［J］. 电工技术学报，2016，31（7）: 81-91.

［7］ 赵波，薛美东，陈荣柱，等. 高可再生能源渗透率下考虑预测误差的微电网经济调度模型［J］. 电力系统自动化，2014，38（7）: 1-8. DOI: 10.7500/AEPS201210254.

［8］ 撖奥洋，邓星，文明浩，等. 高渗透率下大电网应对微网接入的策略［J］. 电力系统自动化，2010，34（1）: 78-83.

［9］ 王颖，文福拴，赵波，等. 高密度分布式光伏接入下电压越限问题的分析与对策［J］. 中国电机工程学报，2016，36（5）: 1200-1206. DOI: 10.13334/j.0258-8013. pcsee.2016.05.004.

［10］ KASHEM M A，LEDWICH G. Distributed generation as voltage support for single wire earth return systems［J］. IEEE transactions on power delivery，2004，19（3）: 1002-1011. DOI: 10.1109/TPWRD.2003.822977.

［11］ 周念成，邓浩，王强钢，等. 光伏与微型燃气轮机混合微网能量管理研究［J］. 电工技术学报，2012，27（1）: 74-84.

［12］ PUCCI M，CIRRINCIONE M. Neural MPPT control of wind generators with induction machines without speed sensors［J］. IEEE transactions on industrial electronics，2011，58（1）: 37-47. DOI: 10.1109/TIE.2010.2043043.

［13］ 王成山，马力，王守相. 基于双PWM换流器的微型燃气轮机系统仿真［J］. 电力系统自动化，2008，32（1）: 56-60. DOI: 10.3321/j.issn:1000-1026.2008.01.013.

［14］ 陈秋南，韦钢，朱昊，等. 风电/微型燃气轮机混合微电网电压波动优化控制［J］. 电力系统自动化，2014，38（9）: 226-231. DOI: 10.7500/AEPS20130823003.

［15］ JURADO F. Modelling micro-turbines using Hammerstein models［J］. International journal of energy research，2005，29（9）: 841-855. DOI: 10.1002/er.1102.

［16］ 刘君，穆世霞，李岩松，等. 微电网中微型燃气轮机发电系统整体建模与仿真［J］. 电力系统自动化，2010，34（7）: 85-89.

［17］ 张继元，舒杰，吴志峰，等. 微网双向变流器的解耦控制策略研究［J］. 新能源进展，2014，2（6）: 476-480. DOI: 10.3969/j.issn.2095-560X.2014.06.011.

［18］ 张庆海，彭楚武，陈燕东，等. 一种微电网多逆变器并联运行控制策略［J］. 中国电机工程学报，2012，32（25）: 126-132.

［19］ ZHONG Q C，WEISS G. Synchronverters: inverters that mimic synchronous generators［J］. IEEE transactions on industrial electronics，2011，58（4）: 1259-1267. DOI: 10.1109/TIE.2010.2048839.

［20］ 李斌，刘天琪，李兴源. 分布式电源接入对系统电压稳定性的影响［J］. 电网技术，2009，33（3）: 84-88.

［21］ 符杨，胡鹏，汤波，等. 微网对电网稳定性影响的仿真与分析［J］. 电源技术，2015，39（3）: 556-560. DOI: 10.3969/j.issn.1002-087X.2015.03.036.

［22］ 周双喜，朱凌志，郭锡玖，等. 电力系统电压稳定性及其控制［M］. 北京: 中国电力出版社，2004.

Impacts of Distributed Generations with High Penetration Level on Voltage Stability of Power System

ZHANG Ji-yuan1，2，3，4，HUANG Lei1，2，3，4，SHU Jie1，2，3，WANG Hao1，2，3，DING Jian-ning5
（1. Guangzhou Institute of Energy Conversion，Chinese Academy of Sciences，Guangzhou 510640，China；2. Key Laboratory of Renewable Energy，Chinese Academy of Sciences，Guangzhou 510640，China；3. Guangdong Provincial Key Laboratory of New and Renewable Energy Research and Development，Guangzhou 510640，China；4. University of Chinese Academy of Sciences，Beijing 100049，China；5. Jiangsu Collaborative Innovation Center of Photovoltaic Science and Engineering，Jiangsu Changzhou 213164，China）

In order to investigate the impacts of distributed generation （DG） with high penetration level on voltage stability of power system，this paper focuses on the characteristics of different DGs，presents corresponding grid-tied control strategies and the DG generators’ dynamic model. Theoretical analysis and numerical study was conducted for the effects of the grid-connection DGs on the grid static voltage，dynamic characteristics of DG speed and frequency under different penetration levels，as well as the impacts of DGs with different control strategies on the power system during the fault. The results show that micro-grid can provide voltage support，but with the penetration increases it generates negative effect on grid stability；and the voltage source DGs can promote the recovery of grid voltage and frequency after the fault.

distributed generation；high penetration level；control strategy；static voltage；dynamic characteristics

TK01+9；TM712

A

10.3969/j.issn.2095-560X.2016.05.007

2095-560X（2016）05-0379-07

张继元（1990-），男，博士研究生，助理研究员，主要从事电力电子技术在电力系统中的应用。

黄 磊（1986-），女，博士研究生，助理研究员，主要从事可再生能源发电预测、微电网仿真技术和能量管理研究。

舒 杰（1969-），男，博士，研究员，主要从事可再生能源及微电网技术研究。

2016-07-18

2016-09-18

广州市创新平台建设与共享专项（201509010018）；佛山市院市合作项目（2014HK100051）；中国科学院广州能源研究所所长创新培育基金（y407pa1001）；广东省协同创新与平台环境建设项目（2014B040404002）

† 通信作者：舒 杰，E-mail：shujie@ms.giec.ac.cn