A-调和方程与微分形式关系

顾志华,陈亚婷

(河北农业大学理学院，河北保定　071001)



A-调和方程与微分形式关系

顾志华,陈亚婷

(河北农业大学理学院，河北保定071001)

A-调和方程和微分形式在电磁学与流体力学中占有重要的地位，研究他们之间的关系尤为重要.介绍了2类加权微分形式，并证明了微分形式与A-调和方程之间的关系.

A-调和方程；黎曼流形； 微分形式；算子

MSC2010:43A15；35J60

A-调和方程理论在偏微分方程、位势理论和拟共形分析等领域发挥着非常重要的作用.求解调和方程是电磁学、流体力学和天文学等领域经常遇到的一类重要的数学问题,其中A-调和方程解的性质为研究的重点[1-6].而流形上的微分形式在物理学科也有着特殊的意义,所以研究调和方程与微分形式之间的关系也显得尤为重要.近几年中，A-调和形式理论的研究已经取得了显着的进步.该理论的结论以及它们的应用已经被发现[7-9].在本文中，引入了2类微分形式，这2类微分表达式与拟线性椭圆方程之间有着密切的关系.本文中用到的符号、表述都可以在文献[9]中见到.

设M和N是C3类的黎曼流形，算子*：∧k(M)→∧n-k(M)称为Hodge星算子，具有以下性质：对于任意的α，β∈∧k(M)，a,b∈R,*(aα+bβ)=a*α+b*β,对于任意的γ∈∧k(M)，有*(*γ)=(-1)k(n-k)γ.对于任意的α，β∈∧k(M)，內积〈α,β〉=*-1〈α,*β〉=*(α∧*β),Hodge星算子的逆算子记为*-1，满足*-1(*γ)=*(*-1γ)=γ.

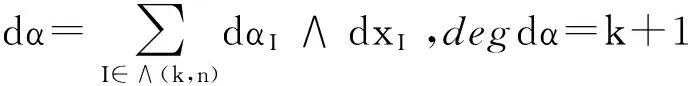
E-mail:guzhihuahbu@163.com

设ω(x)为权函数，若ω(x)∈Lloc(M)，ω(x)>0，则μ(E)=∫Eω(x)dx.

1　黎曼流形上的微分形式

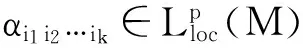
(1)

则称α是弱闭的微分形式.

定义2设γ是黎曼流形M上弱闭的微分形式，

(2)

若存在弱闭的微分形式θ，

(3)

使得几乎处处有

v0|θ|q≤ωq-1〈γ，*θ〉+v1ωq|θ|,

(4)

其中v0、v1是常数,则称γ是黎曼流形M上的DF1类.

定义3设γ是黎曼流形M上满足(2)的弱闭的微分形式，若存在弱闭的微分形式(3)，使得几乎处处有

(5)

和

|θ|≤v3ω|γ|p-1,

(6)

其中v2、v3是常数，则称γ是黎曼流形M上的DF2类.

定理1DF1和DF2满足DF2⊂DF1.

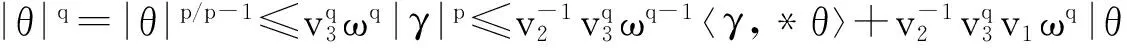
2　拟线性椭圆方程

设A:Λk(T(M))→Λk(T(M))是定义在k维切向量空间的Λk(T(M))的映射，即对于几乎处处的点m∈M，映射A(m,·):ξ∈Λk(T(M))→Λk(T(M)).假设对于几乎处处的点m∈M和任意ξ∈Λk(T(M))，

(7)

其中常数q>1,v0、v1>0.

(8)

(9)

证明：设微分形式γ，degγ=k-1是式(8)的弱解，即满足式(9)，微分形式α(m)在点m处等于A(m,dγ)，且θ=*-1α.由POINCARE′引理知dγ是弱闭的微分形式，且θ满足下式

满足式(4).证毕.

假设A(m,ξ)满足

(10)

(11)

其中v1、v2、v3是常数.

证明：θ、dγ的假设如同定理2，由式(10)和式(11)可得

相反，若dγ∈DF2，则存在弱闭的微分形式θ(满足式(5)和式(6)).

定义

其中α=*θ，则由弱闭的微分形式θ可得到γ是式(8)的弱解，且由式(5)、(6)得式(10)、(11)成立.

[1]IWANIECT,MARTING.Geometricfunctiontheoryandnonlinearanalysis[M].Oxford:ClarendonPress，2001.

[2]佟玉霞,徐秀娟,朱新华，等.A-调和方程弱解的双权Caccioppoli型不等式[J].数学的实践与认识,2007,37(03):130-134.DOI:10.3969/j.issn.1000-0984.2007.03.023.TONGYuxia,XUXiujuan,ZHUXinhua,etal.Two-weightCaccioppolitypeinequalityforweaksolutionstoA-harmonicequation[J].MathematicsinPracticeandTheory2007,37(03):130-134.DOI:10.3969/j.issn.1000-0984.2007.03.023.

[3]高红亚.A-调和方程很弱解的正则性[J].数学学报,2001,44(04):605-610.DOI:10.3321/j.issn.0583-1431.2001.04.005.

GAOHongya.RegularityforveryweaksolutionsofA-harmonicequations[J].ActaMathematicSincia,2001,44(04):605-610.DOI:10.3321/j.issn.0583-1431.2001.04.005.

[4]GAOHongya,CHENYinzhu.CaccioppoliytypeinequalityforweaksolutionsofA-harmonicequationanditsapplications[J].KyungpookMathmaticJournal,2004,44(3):363-368.

[5]高红亚,王岷,赵洪亮.A-调和方程障碍问题的很弱解[J].数学研究与评论,2004,24(1):159-167.DOI:10.3770/j.issn.2095-2651.2004.01.022.

GAOHongya,WANGMin,ZHAOHongliang.VeryweaksolutionsforobstacleproblemsofA-harmonicequation[J].JournalofMathematicalResearchandExposition,2004,24(1):159-167.DOI:10.3770/j.issn.2095-2651.2004.01.022.

[6]TUTL,MOJ.Interpolationsolutiontoaboundaryvalueproblemofharmonicfield[J].ActaMathematicaScientia,2013,33B(2):321-332.DOI:10.3969/j.issn.0252-9602.2013.02.001.

[7]包革军,李天祥,邢宇明.共轭A-调和张量的双权Hardy-Littlewood不等式[J].数学年刊A辑,2005,26A(1):113-120.DOI:10.3321/j.issn.1000-8134.2005.01.014.

BAOGejun,LITianxiang,XINGYuming.Two-weightedHardy-LittlewoodinequalityforA-harmonictensors[J].ChineseAnnalsofMathematics,SeriesA,2005,26A(1):113-120.DOI:10.3321/j.issn.1000-8134.2005.01.014.

[8]郑神州,舒连青.逼近双调和映射的紧性[J].北京交通大学学报(自然科学版),2012,36(6):137-140.DOI:10.3969/j.issn.1673-0291.2012.06.026.

ZHENGShenzhou,SHULianqing.Compactnessofapproximatebiharmonicmaps[J].JournalofBeijingJiaotongUniversity(NaturalScienceEdition),2012,36(6):137-140.DOI:10.3969/j.issn.1673-0291.2012.06.026.

[9]商秀印,顾志华.黎曼流形上微分形式的WT类[J].河北大学学报(自然科学版),2010,30(3):239-241.

SHANGXiuyin,GUZhihua.WeightedWT-classesofdifferentialformsonRiemannianmanifolds[J].JournalofHebeiUniversity(NaturalScienceEdition),2010,30(3):239-241.

(责任编辑：王兰英)

RelationshipbetweenA-harmonicequationanddifferentialform

GUZhihua,CHENYating

(CollegeofScience,AgriculturalUniversityofHebei,Baoding071001,China)

A-Harmonicequationanddifferentialformsareveryimportantinelectromagneticandfluidmechanics,andtheirrelationshipisparticularlyimportant.Thispaperintroducestwotypesofweighteddifferentialforms,andprovestherelationshipbetweendifferentialformandA-harmonicequation.

A-harmonicequation;Riemannianmanifold;differentialform;operator

10.3969/j.issn.1000-1565.2016.03.002

2015-04-18

保定市科学技术研究与发展计划指导项目(12ZS005；12ZS006；14ZN001)；河北省高等学校科学技术研究青年基金项目(QN2016243)

顾志华(1981-)，女，河北邯郸人，河北农业大学讲师，主要从事偏微分方程的研究.

O

A