不具有磁扩散的磁流体方程组的最新进展

向昭银

（电子科技大学　数学科学学院，成都 611731）

不具有磁扩散的磁流体方程组的最新进展

向昭银

（电子科技大学数学科学学院，成都 611731）

不具有磁扩散的磁流体方程组可以用于描述高温等离子体的强烈碰撞或者碰撞所产生的阻尼很小的磁流体运动。本文主要对不具有磁扩散的磁流体方程组经典解的整体存在性等问题的最新研究进展进行了综述，并提出了一些值得进一步深入研究的公开问题.

磁流体方程组；磁扩散；经典解；整体存在性

0 引 言

在本文中，我们将综述如下不可压缩磁流体方程组解的局部、整体存在性与大时间行为等方面的研究进展：

其中Ω⊂ℝd。这里，B和 u分别表示磁场和流体速度场，p是相应的压力，μ和 ν分别代表磁扩散系数和动力学粘性系数。

磁流体方程组（1）描述了导电流体在磁场中运动时磁场与流体相互作用的动力学行为。在方程组（1）的第三个方程中，▽·B=0反映了不存在磁单极，它可以由初始时刻磁单极的不存在性所确定；▽·u=0反映了流体的不可压缩性质；若记E为电场，j为电流密度，σ为介质的电导率，则方程组（1）的第一个方程可以在安培定律▽×B=ε∂tE+j中忽略位移电流（即ε=0），结合法拉第定律▽×E=-∂tB、欧姆定律j=σ（E+u×B）并取μ∶=1/σ所得到；方程组（1）中的第二个方程是具有外力作用的Navier-Stokes方程，它描述了动量守恒，其中外力为洛伦兹力j×B。

物理学家Alfven于上世纪40年代建立了磁流体力学［1］，并因此获得了1970年的Nobel物理学奖。数学上的研究起源于上世纪70年代。四十多年来，关于方程组（1）的解的存在唯一性等问题，已经取得了许多重要的进展。

1 关于具有磁扩散的磁流体方程组的研究

在完全耗散（即μ＞0且ν＞0）情形，Duvaut和Lions［2］在Sobolev空间HS（ℝd）中证明了方程组（1）的Cauchy问题经典解的局部存在性、唯一性以及小初值解的整体存在性。最近，Abidi和Paicu［3］在临界空间框架下研究了非齐次介质中的磁流体方程组（1），得到了类似于文献［2］的结果。在二维情形，Sermange和Temam［4］进一步证明了方程组（1）的Cauchy问题对于大初值，解也是整体存在的。由于三维Navier-Stokes方程大初值经典解的整体存在性是一个公开的问题，因此三维情形方程组（1）经典解的整体存在性也是一个公开问题。最近，He，Huang和Wang［5］等证明了对于大初值，只要初始磁场和初始速度场的差比较小，方程组（1）的Cauchy问题在三维情形仍存在整体经典解。另一方面，Jiu和Liu［6］也对具有某种径向对称结构的大初值，建立了方程组（1）Cauchy问题解的整体存在。具有完全耗散的方程组（1）在初边值条件下的相应问题也有许多重要的进展，上述有关Cauchy问题的大部分结论仍成立。

一个自然的问题是，对于具有部分耗散（即μ＞0与ν＞0不同时成立）的方程组（1）是否存在整体解？当Ω=ℝ2时，Cao和Wu［7］首次证明了具有混合部分粘性与部分磁扩散的方程组（1）整体经典解的存在唯一性及零粘性情形弱解的整体存在性；随后，Cao，Regm i和Wu［8］进一步证明了具有水平粘性和水平磁扩散的方程组（1）整体经典解的存在唯一性；Du和Zhou［9］则对粘性系数与磁扩散系数进行了更细致的分类，并在各种情形研究了经典解的整体存在性与正则性准则。关于零粘性及分数阶磁扩散方程组（1）经典解整体存在性的研究，我们参考［10—12］。

2 关于不具有磁扩散的磁流体方程组Cauchy问题的研究

值得指出的是，上述的所有研究工作中，为了得到经典解的整体存在性，都或多或少地要求磁场具有一定的扩散。但是，由于等离子体为良导体，即σ≫1。因此在等离子物理的许多研究问题中，都可以假设μ=0，此时方程组（1）可以转化为如下不具有磁扩散形式的磁流体方程组：

事实上，在等离子物理中，基于磁流体波的高温等离子的受热研究是一个相当有趣而具有挑战性的问题。因此，不具有磁扩散的磁流体方程组（2）可以用于描述高温等离子体的强烈碰撞或者由于碰撞所产生的阻尼很小的磁流体运动。

近年来，磁流体力学方程组（2）的数学理论也吸引了许多数学家的高度关注。对于光滑初值，利用标准的能量方法很容易证明解的局部存在性与唯一性。最近，许多数学家在低正则初值假设之下研究了局部适定性问题。例如，Fefferman等［13］通过建立一个新的交换子估计，在中证明了方程组（2）局部解的存在唯一性，其中，d=2，3；Chemin等［14］则在临界Besov空间中证明了局部解的存在性及d=3时的唯一性；Wan［15］进一步证明了d=2时的唯一性。

一个长期的公开问题是：不具有磁扩散的磁流体方程组（2）是否存在整体经典解？Bardos，Sulem和Sulem［16］证明了，对于强的背景磁场及小的局部化初始摄动，理想磁流体方程组（即方程组（2）中ν=0）存在光滑整体解且当t→∞时，非线性的相互作用是可以渐进忽略的。但是，Bardos等这种基于特征的方法不能应用于方程组（2）。Chiuderi和Califano［17］则从数值上证明了二维磁流体方程组（2）具有不依赖于欧姆电阻的能量耗散率。

在数学理论方面的研究，Lin和Zhang［18］取得了第一个突破。他们利用各向异性的Besov空间和Littlewood-Paley分解技巧对如下三维磁流体形式的方程组 Cauchy问题在平衡态（ø-，u-）=（x3，0）附近建立了解的经典解的整体存在性：

随后，Lin和Zhang［19］利用基本的能量方法对（3）建立了经典解的整体存在性，从而简化了文献［18］的证明；而Ren，Xiang和Zhang［20］则给出了基于基本的能量方法的简化证明及衰减估计。对方程组（3）的研究有两方面的意义：其一是方程组（3）与粘弹性流体方程具有相似的非线性结构，事实上，若ø为向量，则（3）就是标准的粘弹性流体方程；其二是在二维情形，由▽·B=0可知存在势函数ø使得B=（∂2ø-∂1ø），从而方程组（3）在二维情形等价于不具有磁扩散的磁流体方程组（2）。关于不具有磁扩散的二维磁流体方程组（2）的第一个数学结果属于Lin，Xu和Zhang［21］。他们利用Lagrange坐标和各向异性的Besov空间技巧证明了方程组（2）的Cauchy问题在平衡态（，）=（e1，0）附近存在整体经典解；随后，Zhang［22］给了一个基于基本能量方法的证明；Ren等［23］则进一步建立了解的衰减估计。最近，Zhang［24］证明了对于大初值，只要背景磁场充分强，方程组（2）仍存在整体强解；对在二维情形的相关工作，我们也参考［25，26］。关于不具有磁扩散的三维磁流体方程组（2）的Cauchy问题，Xu和Zhang［27］证明了对于一类具有某种相容性条件的初值，在平衡态（，）=（e1，0）附近存在整体经典解；Abidi和Zhang［28］则进一步去掉了关于初值的相容性限制。关于三维情形不具有磁扩散的磁流体方程组（2）在的大初值条件下的整体存在性问题，最近也有一些深入研究。比如，Lei［29］考虑方程组（2）在磁场旋转且垂直于速度场（即在球面坐标系下uθ=Br=BZ=0）情形有限能量解的整体存在性；Jiu等［30］以代替△u，并得到了类似于［29］的结果。

3 关于不具有磁扩散的磁流体方程组初边值问题的研究

上述有关不具有磁扩散的磁流体方程组经典解的整体存在性都是针对Cauchy问题，并不涉及边界条件。事实上，对于方程组（2）的初边值问题而言，关于Cauchy问题的研究技巧并不适用。

与速度场具有滑动边界条件、磁场具有非穿透边界条件

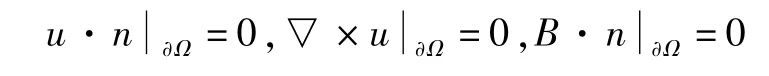
4 关于不具有磁扩散的磁流体方程组的一些公开问题

关于不具有磁扩散的磁流体方程组（2），存在大量尚未解决的公开问题。这里仅仅提出几个作者感兴趣的问题：

1）Cauchy问题大初值解的整体存在性；

2）在一般边界条件下初边值问题解的整体存在性；

3）自由边值问题解的整体存在性；

4）整体经典解的衰减估计等大时间行为；

5）粘性极限（即ν→0）问题。

［1］ALFVEN H.Existence of electromagnetic-hydrodynamic waves［J］.Nature.1942，150：405-406.

［2］DUVAUT G，LIONS J L.Inéquations en thermoelasticitéetmagnétohydrodynamique［J］.Arch.Rational Mech.Anal.，1972，46：241-279.

［3］ABIDIH，PAICU M.Global existence for the magnetohydrodynamic system in critical spaces［J］.Proc.Roy.Soc.Edinburgh Sect.A，2008，138：447-476.

［4］SERMANGE M，TEMAM R.Some mathematical questions related to the MHD equations［J］.Comm.Pure App l.Math.，1983，36：635-664.

［5］HE C，HUANG X，WANG Y.On some new global existence results for 3D magnetohydrodynamic equations［J］.Nonlinearity，2014，27：343-352.

［6］JIU Q，LIU J.Global regularity for the 3D axisymmetric MHD Equations with horizontal dissipation and vertical magnetic diffu-sion［J］.Disc.Cont.Dyn.Sys.-Series A，2015，35：301-322.

［7］CAO C，WU J.Global regularity for the 2D MHD equations with mixed partial dissipation and magnetic diffusion［J］.Adv. Math.，2011，226：1803-1822.

［8］CAO C，REGMID，WU J.The 2D MHD equations with horizontal dissipation and horizontalmagnetic diffusion［J］.J.Differential Equations，2013，254：2661-2681.

［9］DU L，ZHOU D.Global well-posedness of two-dimensionalmagnetohydrodynamic flows with partial dissipation and magnetic diffusion［J］.SIAM J.Math.Anal.，2015，47：1562-1589.

［10］CAO C，WU J，YUAN B.The 2D incompressible magnetohydrodynamics equations with only magnetic diffusion［J］.SIAM J. Math.Anal.，2014，46：588-602.

［11］JIU Q，ZHAO J.Global regularity of2D generalized MHD equationswith magnetic diffusion［J］.Z.Angew.Math.Phys.，2015，66：677-687.

［12］TRAN C，YU X，ZHAIZ.On global regularity of 2D generalized magnetohydrodynam ic equations［J］.J.Differential Equations，2013，254：4194-4216.

［13］FEFFERMAN C，MCCORM ICK D，ROBINSON J，et al.Higher order commutator estimates and local existence for the non-resistive MHD equations and related models［J］.J.Functional Analysis，2014，267：1035-1056.

［14］CHEMIN J，MCCORMICK D，ROBINSON J，et al.Local existence for the non-resistive MHD equations in Besov spaces［J］. Adv.Math.，2016，286：1-31.

［15］WAN R.On the uniqueness for the 2D MHD equations withoutmagnetic diffusion［DB/OL］.Eprint arXiv，2015，arXiv：1503. 03589.

［16］BARDOSC，SULEM C，SULEM P.Longtime dynam ics of a counductive fluid in the presence of a strong magnetic field［J］. Trans.Amer.Math.Soc.，1988，305：175-191.

［17］CALIFANO F，CHIUDERIC.Resistivity-independent dissipation ofmagnetrodydrodynam ic waves in an inhomogeneous plasma［J］.Phy.Rev.E，1999，60：4701-4707.

［18］LIN F，ZHANG P.Global small solutions to MHD type system（I）：3-D case［J］.Comm.Pure.Appl.Math，2014，67：531-580.

［19］LIN F，ZHANG T.Global small solutions to a complex fluid model in 3D［J］.Arch.Rational Mech.Anal.，2015，216：905-920.

［20］REN X，XIANG Z，ZHANG Z.Decay of smooth solution for the 3D MHD-type equationswithoutmagnetic diffusion［J］.Science China Mathematics，2016，to appear.

［21］LIN F，XU L，ZHANG P.Global small solutions of 2-D incompressible MHD system［J］.J.Differential Equations，2015，259：5440-5485.

［22］ZHANG T.An elementary proof of the global existence and uniqueness theorem to 2-D incompressible non-resistive MHD system［EB/OL］.（2014-04-23）［1015-11-20］.http：//arxiv.org/pdf/1404.5681V2.pdf.

［23］REN X，WU J，XIANG Z，ZHANG Z.Global existence and decay of smooth solution for the 2-D MHD equations withoutmagne tic diffusion［J］.J.Functional Analysis，2014，267：503-541.

［24］ZHANG T.Global solutions to the 2D viscous，non-resistive MHD system with large background magnetic field［J］.J.Differen tial Equations.2016，http：//dx.doi.org/10.1016/j.jde.2015.12.005

［25］HU X，LIN F.Global existence for two dimensional incompressible magnetohydrodynamic flows with zero magnetic diffusivity［EB/OL］.（2014-05-01）［2015-12-01］.http：//arxiv.org/pd f/140s.0082V1.pdf.

［26］WU J，WU Y，XU X.Global small solution to the 2D MHD system with a velocity damping term［J］.SIAM J.Math.Anal.，2015，47：2630-2656.

［27］XU L，ZHANG P.Global small solutions to three dimensional incompressible MHD system［J］.SIAM J.Math.Anal.，2015，47：26-65.

［28］ABIDIH，ZHANG P.On the global solution of 3-D MHD system with initial data near equilibrium［EB/OL］.（2015-11-10）［2015-12-01］.http：//arxiv.org/pdf/1511.02978v1.pdf

［29］LEI Z.On axially symmetric incompressible magnetohydrodynam ics in three dimensions［J］.J.Differential Equations，2015，259：3202-3215.

［30］JIU Q，YU H，ZHENG X.Global well-posedness for axisymmetric MHD system with only vertical viscosity［EB/OL］.（2015-07-09）［2015-12-01］.http：//arxiv.org/pdf/1507.02468.pdf.

［31］REN X，XIANG Z，ZHANG Z.Global well-posedness for the 2D MHD equations withoutmagnetic diffusion in a strip domain［J］.Nonlinearity，2016，to appear.

［32］TAN Z，WANG Y.Global well-posedness of an initial-boundary value problem for viscous non-resistive MHD systems［EB/ OL］.（2015-11-24）［2015-12-1］，http：//arxiv/pdf/1509.08349V3.pdf.

Recent Studies on the MHD EquationsW ithout M agnetic Diffusion

XIANG Zhaoyin
（School of Mathematical Sciences，University of Electronic Science and Technology of China，Chengdu 611731，China）

The MHD equations without magnetic diffusion can be applied tothe description of strong p lasma collisions or the extremely small resistivity due to these collisions.In this article，the recent studies on the MHD equations withoutmagnetic diffusion are exam ined，exposing several issues still in this area.

MHD equations；zero magnetic diffusion；classical solution；global existence

O175.2

A

10.16246/j.issn.1673-5072.2016.01.018

1673-5072（2016）01-0120-05

2016-01-11

国家自然科学基金项目（11571063）

向昭银（1978—），男，四川合江人，博士，教授，博士生导师，主要从事偏微分方程研究。

向昭银，E-mail：zxiang@uestc.edu.cn