现有洪水中人体失稳标准的评价及改进

夏军强， 陈　倩， 李　娜， 果　鹏

(1. 武汉大学 水资源与水电工程科学国家重点实验室， 湖北 武汉 430072； 2. 中国水利水电科学研究院 防洪抗旱减灾研究所， 北京 100038)



现有洪水中人体失稳标准的评价及改进

夏军强1， 陈倩1， 李娜2， 果鹏1

(1. 武汉大学 水资源与水电工程科学国家重点实验室， 湖北 武汉 430072； 2. 中国水利水电科学研究院 防洪抗旱减灾研究所， 北京 100038)

近年来城市洪涝灾害频繁发生，导致人员伤亡严重，因此研究洪水中人体失稳标准可为城市洪水风险管理提供科学参考.全面总结了已有洪水中人体失稳的试验研究及力学理论分析成果，表明现有基于水槽试验的洪水中人体失稳标准大多数不考虑失稳机理，而部分理论分析结果通常忽略人体所受浮力并且假定来流沿水深为均匀分布，与实际情况不符.当前较新研究成果尽管克服了上述不足，但忽略欧美人体结构与中国人体的差异，所以还需进一步完善.故有必要对洪水中人体的失稳标准进行改进.采用欧美人体结构的特征参数，修正了洪水中人体所受浮力的计算公式.利用已有洪水中真实人体失稳的水槽试验数据重新率定了人体起动流速公式中的相关参数，提出了改进后的洪水中人体失稳标准，并用城市洪水的实测资料对其进行验证.由于参数率定时采用水槽试验数据，其试验条件比真实洪水过程简单，故所提出的洪水中人体失稳标准偏于危险.

城市洪水； 人体失稳标准； 公式评价； 起动流速； 参数率定

全球气候变化和城市化进程加快改变了城市水循环过程，加剧了城市暴雨洪涝问题[1-2].在我国由暴雨引发的城市洪涝灾害频繁发生，人员伤亡严重.2012年7月北京发生特大暴雨洪水，2d内造成近80人死亡[3].洪水灾害已成为当今世界最主要的灾害之一，具有发生频率高、影响范围广等特点[4].据国际灾难数据库(EM-DAT)统计，1986～2015年间，全球共报道了3 557场次洪水，造成了20.3万人死亡.在水流作用下人体失去稳定是导致洪水中人员伤亡严重的重要原因之一.人类活动范围的扩大和极端天气事件的频繁发生，加大了人们承受洪水灾害的风险[5].因此有必要进一步研究洪水中人体的失稳条件，提出具有更好适用性的失稳标准.

洪水中人体失稳标准的研究成果主要是通过室内水槽试验，包括以儿童为测试对象的研究[6-7]和以成人为测试对象的研究[8-10]；另有一部分成果来自现场试验，包括Jonkman等[11]、Chanson等[12]的研究.以往所提出的基于水槽试验成果的洪水中人体失稳标准大多未涉及人体失稳的动力学机制，而是直接利用试验数据拟合得到水深流速之积与人的身高体重之积之间的经验关系.Jonkman等[11]虽然进行了理论分析，但忽略了人体所受浮力并假定来流沿水深均匀分布，使得所提出的标准与实际情况不符.

夏军强等[13]利用人机工程学原理，基于中国人体结构的特征参数，给出了不同水深下人体所受浮力的计算方法；并假定来流沿水深为指数函数分布，运用河流动力学中的泥沙起动理论，推导出洪水中人体滑移和跌倒失稳的起动流速公式.由于已有水槽试验研究大多以欧美人体为测试对象，而欧美人体结构与中国人体存在差异，因此本文在该工作的基础上，利用欧美人体结构的特征参数，修正洪水中人体所受的浮力公式，然后采用已有真实人体失稳的水槽试验数据，重新率定起动流速公式中的相关参数.在此基础上提出改进后的洪水中人体失稳标准，并利用已有的欧美城市洪水的现场实测数据对公式进行验证.

1　前人研究成果

影响洪水中人体稳定性的因素很多，主要包括洪水要素(水深、流速、水温、水流脉动特性、洪水中挟带的漂浮物等)，人体生理及心理要素(身高、体重、穿着、年龄及健康程度等)，地面要素(坡度、粗糙度等)，其他条件(能见度、风速条件等)4个方面[11].不同学者在开展洪水中人体稳定性试验时尽管采用的控制条件有所不同，但都考虑了以下影响因素：人的身高、体重，来流的水深及流速，并提出了相应的失稳标准.

1.1水槽试验成果

Foster和Cox[6]以6位9～13岁的男孩为试验对象，研究了洪水中儿童在站立和坐下2种情况时的稳定性.试验结果表明：坐下比站立时稳定性差；站立时测试对象体重越大稳定性越好.因该试验以儿童心理上感到不安全作为失稳判别标准，故所得结果适用范围有限.Yee[7]通过水槽试验同样研究了洪水中儿童的稳定性.该试验水槽底坡坡度为1%，测试对象为2名男童和2名女童，年龄在4～7岁，试验时均穿泳装，不穿鞋.以测试对象滑移或跌倒失稳不能继续试验，或者在来流冲击下感到不适作为失稳判定条件.试验结果表明：人体失稳时临界水深与流速之积受测试对象年龄影响变化很大，年龄最小的4号测试对象由于身体尚未发育完全，抵抗水流冲击能力远小于其他3位年龄较大的测试者.

Abt等[8]在水槽试验中考虑4种地面材料和2种底坡情况，以简化人体模型和20名成人为测试对象，研究了成人在洪水中的失稳条件.由于真实人体在水流作用下能调整站立姿势，研究发现成人抵抗水流冲击能力比模型高出60%～120%.通过对试验数据进行拟合，Abt等[8]得出失稳时水深和流速之积与人的身高体重之积之间的指数关系(见表1).表中：hf为水深；Uc为临界流速；hp，mp分别为人体身高和体重.该公式没有考虑洪水中人体失稳的动力学机理.Karvonen等[9]在一个大型水池中开展洪水中人体失稳试验，测试对象站在可移动钢架平台上，利用拖车牵引可移动平台来产生人体与水流的相对运动.通过对试验结果分析，Karvonen等[9]按水流情况、人体状况、鞋底与地面的接触情况、光线等条件定性将外界环境划分为较好、一般、较差3种情况，并提出对应于这3种情况时的来流单宽流量与人体身高体重之积之间的线性关系(见表1).Takahashi等[10]测量了3名成年人在水流作用下受到的拖曳力及摩擦力等，讨论了在不同来流方向、穿着及地面材料情况下的人体稳定性，并给出了不同地面和鞋底的摩擦力系数及拖曳力系数的变化范围.

1.2现场实测成果

为模拟真实洪水情况，Jonkman等[11]在英国Lea河下游一个渠道内进行试验，该渠道宽70 m，底部为1%的混凝土地面.测试对象是一名专业特技男演员，身高为1.7 m，体重为68 kg.通过试验，Jonkman等[11]进一步解释了洪水中人体的失稳机理，并将人体概化为长方体，通过简单力学分析推导出洪水中人体面对水流时的跌倒和滑移失稳公式(见表1).表中：μ为鞋底与地面间的摩擦因数；g为重力加速度；CD为水流拖曳力系数；B为人体平均宽度；CM，CF为系数；ρ为水的密度.应当指出，Jonkman等[11]的分析中没有考虑人体所受的浮力作用，但实际洪水中当水深较大时浮力影响不能忽略.

表1　已有洪水中人体失稳标准汇总Tab.1　Summary of criteria of human stability in floodwaters

Chanson等[12]用ADV流速仪测量了2011年1月发生在布里斯班真实城市洪水中的水流条件.实测数据表明真实洪水中水深和流速波动很大，且人体失稳时来流单宽流量小于水槽试验值.因此Chanson等[12]认为洪水中人体稳定性还受水流脉动的影响，并提出以瞬时流速和水深作为洪水中人体失稳条件(见表1)，其中U，h为瞬时流速和水深.

1.3前人试验数据及人体失稳公式对比

将已有洪水中人体失稳的计算公式及上述各水槽试验情况进行汇总，结果分别见表1和表2.试验数据及计算曲线比较如图1所示.图1中计算曲线采用欧美成人平均身高(1.77 m)和体重(75.1 kg)绘制，其中Karvonen等[9]公式的计算曲线，如图中两条虚线所示，从上至下分别表示外界环境较好及较差两种情况.

表2　已有洪水中人体失稳水槽试验情况对比Tab.2　Comparison of existing experimental conditions

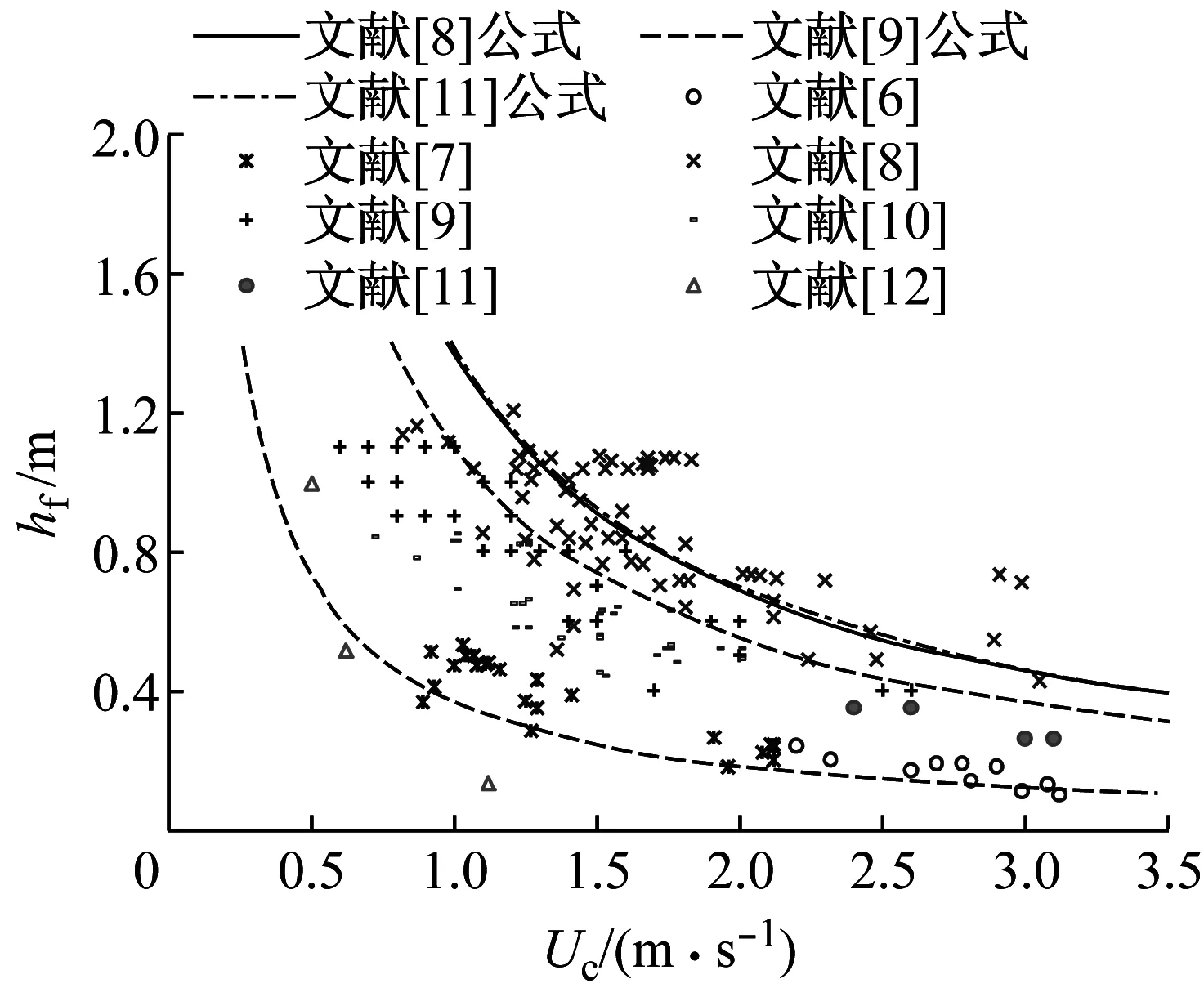
图1　洪水中人体失稳标准对比Fig.1　Comparison of different criteria for human stability in floodwaters

对图1中试验数据分析可知：

(1)由于试验条件差异，Abt等[8]试验所得测试对象的稳定性更好.Abt等[8]试验中测试对象有安全帽、钢绳等防护措施，且测试对象可调整站立姿势以提高抵抗来流冲击的能力；而Takahashi等[10]试验中测试对象没有防护措施，也不能自由移动.Karvonen等[9]的试验对象穿着救生衣，救生衣中存储的空气一方面增大了测试对象受到的浮力作用，另一方面还增加了人体迎流面的作用面积，从而增大了水流拖曳力的作用.Karvonen等[9]的测试对象站在可移动钢架平台上，钢架与鞋底摩擦因数小，不利于人体稳定.测试对象衣着和地面粗糙情况的差异，导致Karvonen等[9]所得的测试对象稳定性在同等来流条件下也低于Abt等[8]的试验结果.

(2)Chanson等[12]试验中人体稳定性明显低于水槽试验结果，这主要是由真实洪水中水深和流速脉动较为剧烈所致.另外，Chanson等[12]试验中测试对象年龄均在49岁以上，比上述水槽试验所用成人测试对象年龄偏大，故抵抗洪水冲击的能力相对较弱.

对图1中的曲线分析可知：由于Jonkman等[11]公式中的参数是由Abt等[8]的试验数据率定得到，取CM=0.16 m2·(s·kg0.5)-1[11]，故Abt等[8]和Jonkman等[11]公式的计算结果相差较小，且相比于其他公式而言，两者的计算结果偏于危险；Karvonen等[9]所提出的较好和较差外界环境时的计算曲线分别与水槽试验和真实洪水的试验数据符合较好，但由于只是定性地区分洪水发生时人体所处环境的好坏，使用时缺少统一的定量标准.同时Abt等[8]和Karvonen等[9]的公式是基于水槽试验数据直接拟合而提出的经验关系，并未涉及实际失稳机理，故计算精度不高，且适用范围有限.Jonkman等[11]公式虽基于力学分析，但对人体受力和来流条件做了过多假设，即未考虑人体所受浮力和流速沿水深方向应为不均匀分布，故计算结果与实际情况不符.

2　现有人体失稳标准的改进

已有研究表明，洪水中人的失稳方式主要有两种：滑移和跌倒[13-14].当来流水深较小但流速较大时，容易发生人体滑移失稳，失稳条件为作用于人体腿部的水流拖曳力大于脚底与地面之间的摩擦力，见图2a；跌倒失稳通常发生在来流水深较大但流速较小的情况下，失稳条件为作用力对人体脚后跟的倾覆力矩大于稳定力矩，见图2b.假设洪水中的人体面朝来流方向，则人体在水平方向上主要承受水流拖曳力FD和地面摩擦力FR作用；在垂直方向上承受自身重力Fg、浮力Fb以及地面的支持力FN作用.

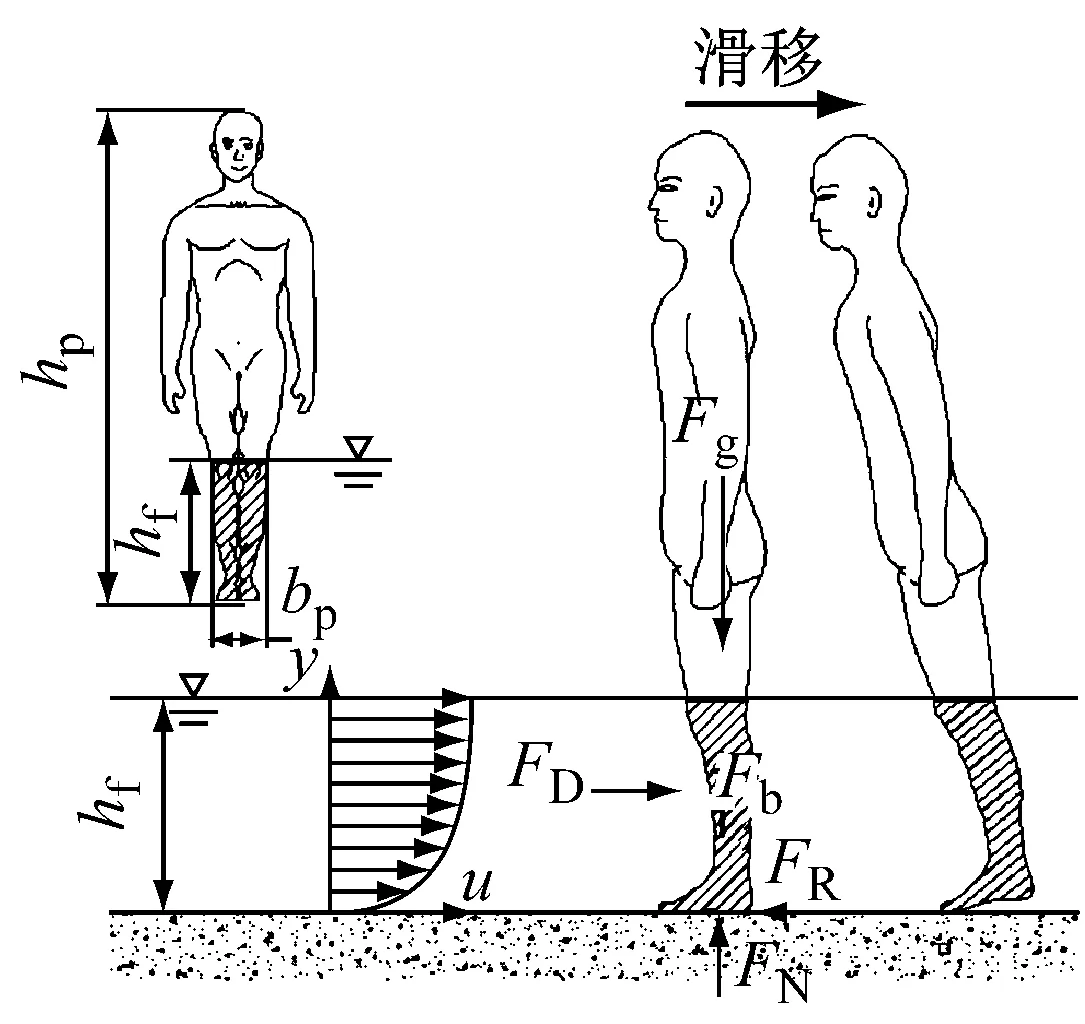
a 滑移失稳

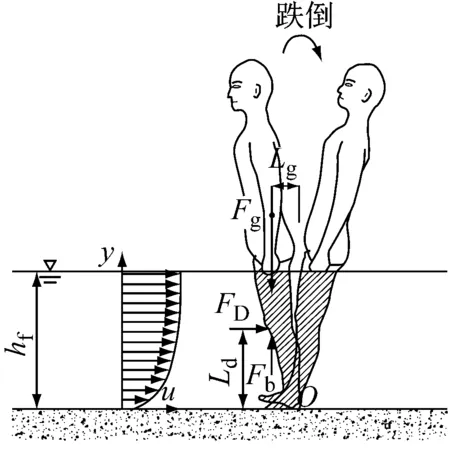
b 跌倒失稳图2　洪水作用下人体受力示意图Fig.2　Governing forces acting on a human body in floodwaters

夏军强等[13]利用河流动力学中泥沙起动理论，推导出了洪水中人体发生滑移及跌倒失稳时的起动流速公式，即

滑移：

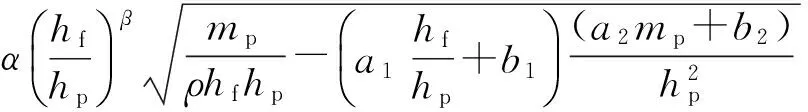
(1)

跌倒：

(2)

式中：α，β均为待率定的参数；a1，b1，a2，b2均为人体结构的特征参数.

上述公式推导中，浮力计算考虑了人体形状沿水深方向的不规则性，利用了人机工程学的原理，得出不同水深下的人体体积，进而求得浮力Fb的计算公式

(3)

式中：x为来流水深hf与人体身高hp之比；a1，b1均为量纲为一的参数，且满足a1+b1=1.根据中国人的平均身体特征参数，率定出a1=0.633，b1=0.367；a2，b2均为表征人体体积与体重之间关系的参数.据人机工程学的统计资料表明，人体体积Vp与体重mp之间存在一定的线性关系[15]，一般可表示为Vp=a2mp+b2，通常情况下可取a2= 1.015×10-3m3·kg-1，b2=-4.937×10-3m3.

由于欧美人体结构与中国人体存在差异，而已有试验研究中大多以欧美人体为测试对象，因此本文采用Harless[16]液浸法测得的人体肢体生物力学参数作为欧美人体结构平均尺寸，重新率定浮力计算式中的参数a1和b1，得a1= 0.735，b1= 0.265.同时人体体积虽因胖瘦和体形不同而有所差异，但由于人体密度差别不大，故存在一般的统计规律[15].因此本文欧美人体体积与体重关系中参数a2，b2取值与中国人体相同.

假定洪水中人体体重为60 kg，当水深达到髋部处，即0.47倍身高，此时人体所受浮力为155 N，达到人体重力的0.26倍，在这种情况下人体的有效质量仅相当于44 kg.由此可见，当水深较大时人体所受浮力较大，可抵消一部分的重力作用，故浮力对洪水中人体稳定性影响较大.因此Jonkman等[11]的研究中忽略人体所受的浮力会带来较大偏差，所以有必要在完善现有洪水中人体失稳标准时更精确地考虑人体所受的浮力作用.

3　公式参数重新率定

将已有洪水中人体失稳的水槽试验数据按滑移和跌倒失稳机制进行划分，分别重新率定起动流速公式(1)及(2)中的参数α，β.其中，式(1)及(2)中人体结构的特征参数采用基于欧美人体尺寸计算所得值.该率定过程分为两部分，首先利用各研究者的试验数据分别率定参数α与β，将率定后式(1)，(2)失稳流速计算值与实测值比较，对公式进行验证；然后综合所有试验数据对参数α，β再次率定，提出改进后的洪水中人体失稳条件.

3.1不同研究者试验数据单独率定

Abt等[8]采用20名成人进行水槽试验，所得的65组数据中有7组发生在流速大、水深小的急流情况，因此认为这7组属于滑移失稳，其余为跌倒失稳.为便于与Jonkman等[11]公式的率定结果比较，取坡度为0.015混凝土地面上的14组数据进行跌倒失稳时的参数率定.Karvonen等[9]测试7名成人在水中采用站立、行走、转弯等不同姿势时的稳定性，共获得38组跌倒失稳数据，考虑到本文所用公式中未考虑转弯情况，故采用除转弯外的34组数据进行率定.Takahashi等[10]共测试了3名成人在不同朝向时站立和坐下时的稳定性，得到滑移和跌倒失稳数据，本文仅采用面向水流站立时的试验数据.Foster和Cox[6]采用6名儿童进行试验共得到14组滑移失稳数据.Yee[7]对4名儿童进行试验，其中4号测试对象仅4岁，其试验结果受儿童生理及心理因素影响较大，故本文仅采用其他3名年龄较大儿童的试验数据.因式(1)及式(2)的公式结构相对较复杂，故采用SPSS软件进行参数率定，得到成人和儿童分别在滑移和跌倒时的参数α及β值，以及计算与实测值的相关系数R2，见表3.

表3　已有水槽试验数据单独率定参数Tab.3　Calibrated parameters using different experimental data

从表3可看出，起动流速公式中参数α，β率定结果有所差异，这主要是由于不同研究者的试验条件及测试对象的个体差异所致.在滑移失稳公式率定中虽然试验数据有限，但公式计算值与实测值仍较为符合(R2>0.5).将本文公式拟合效果与前人进行对比：Abt等[8]建立洪水中人体跌倒失稳时来流单宽流量与其身高体重之积间的经验关系，得到计算与实测值相关系数仅为0.48，小于本文相关系数0.709；Jonkman等[11]通过参数率定方法，得到Abt等[8]试验中滑移和跌倒失稳时计算与实测值的相关系数分别为0.62和0.46，均小于本文相关系数0.630和0.709；同时Jonkman等[11]还得到Karvonen等[9]试验中测试对象跌倒失稳时计算与实测值的相关系数为0.75，拟合效果同样低于本文(R2=0.959).将本文改进后的起动流速公式计算值与实测值绘制于图3中，可见计算与实测值符合良好，说明改进后的起动流速公式能够用于洪水中人体失稳条件的计算.

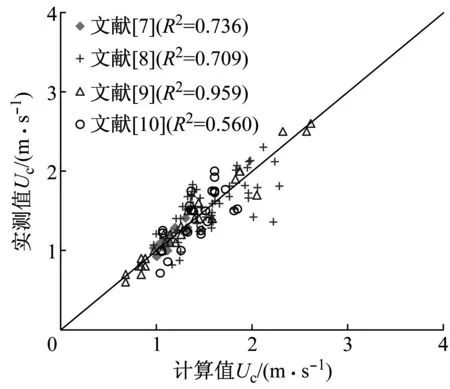
a 跌倒失稳

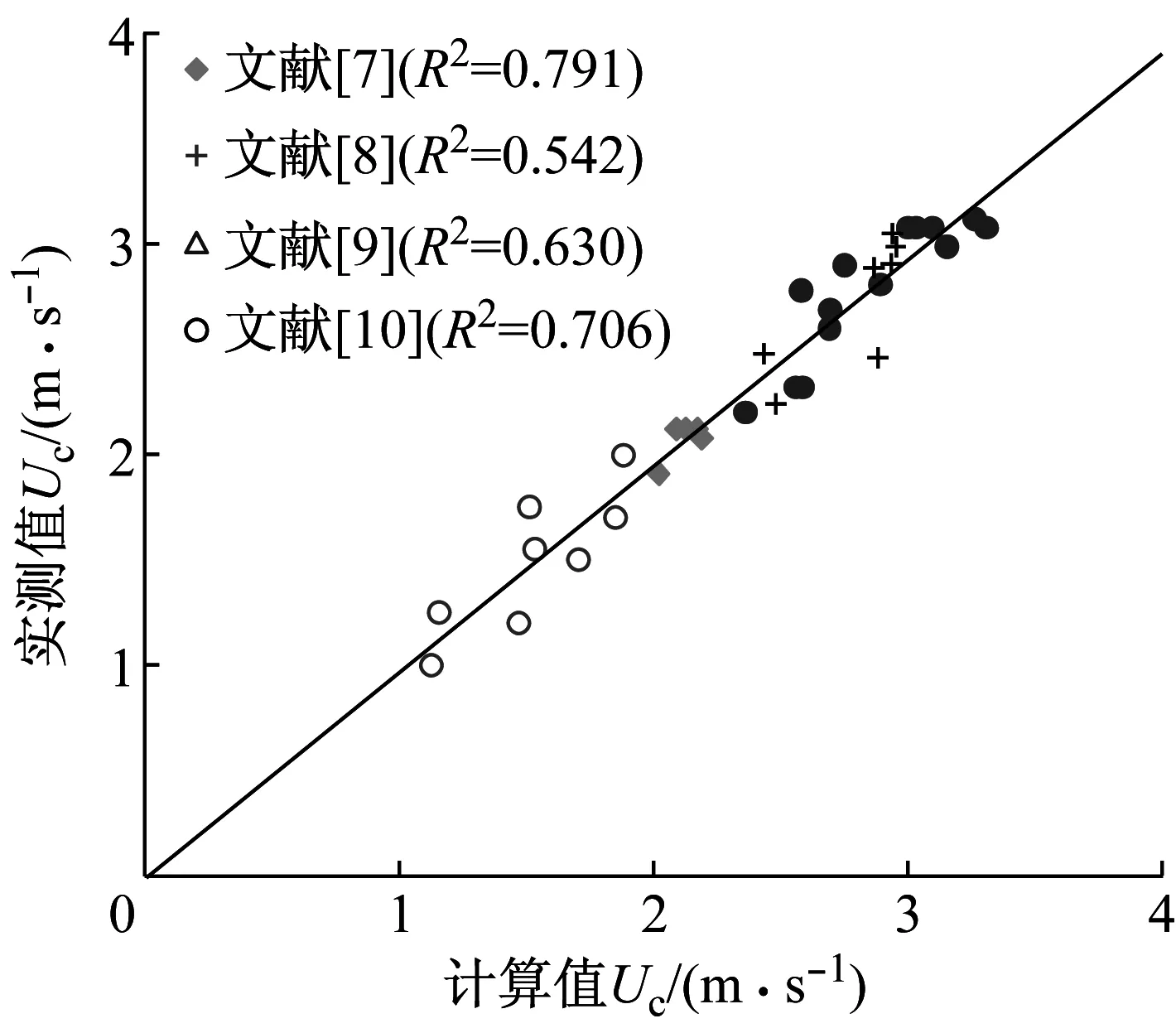
b 滑移失稳图3　不同失稳方式下已有试验数据率定结果Fig.3　Comparisons between calculations using further calibrated formulas and experimental data

3.2所有试验数据综合率定

为提出改进后的洪水中人体失稳标准，需要给定惟一的参数α及β值，因此，本文汇总上述所有水槽试验中的滑移及跌倒失稳数据，分别对式(1)及(2)中的参数进行率定，结果见表4.将率定所得参数代入公式(1)和(2)，同时取欧美成人平均身高1.77 m，体重75.1 kg，儿童平均身高1.26 m，体重25.5 kg，分别绘制成人和儿童在两种失稳条件下起动流速的计算曲线，如图4所示.需要指出的是水槽中试验条件比较理想，如水流恒定且不挟带漂浮物、地面状况良好、测试对象有安全防护措施等，而真实洪水中流动条件较为复杂.因此利用表4中参数计算的起动流速结果，与真实洪水中人体失稳条件相比，偏于危险.

表4　参数率定结果Tab.4　Calibrated parameters using all experimental data

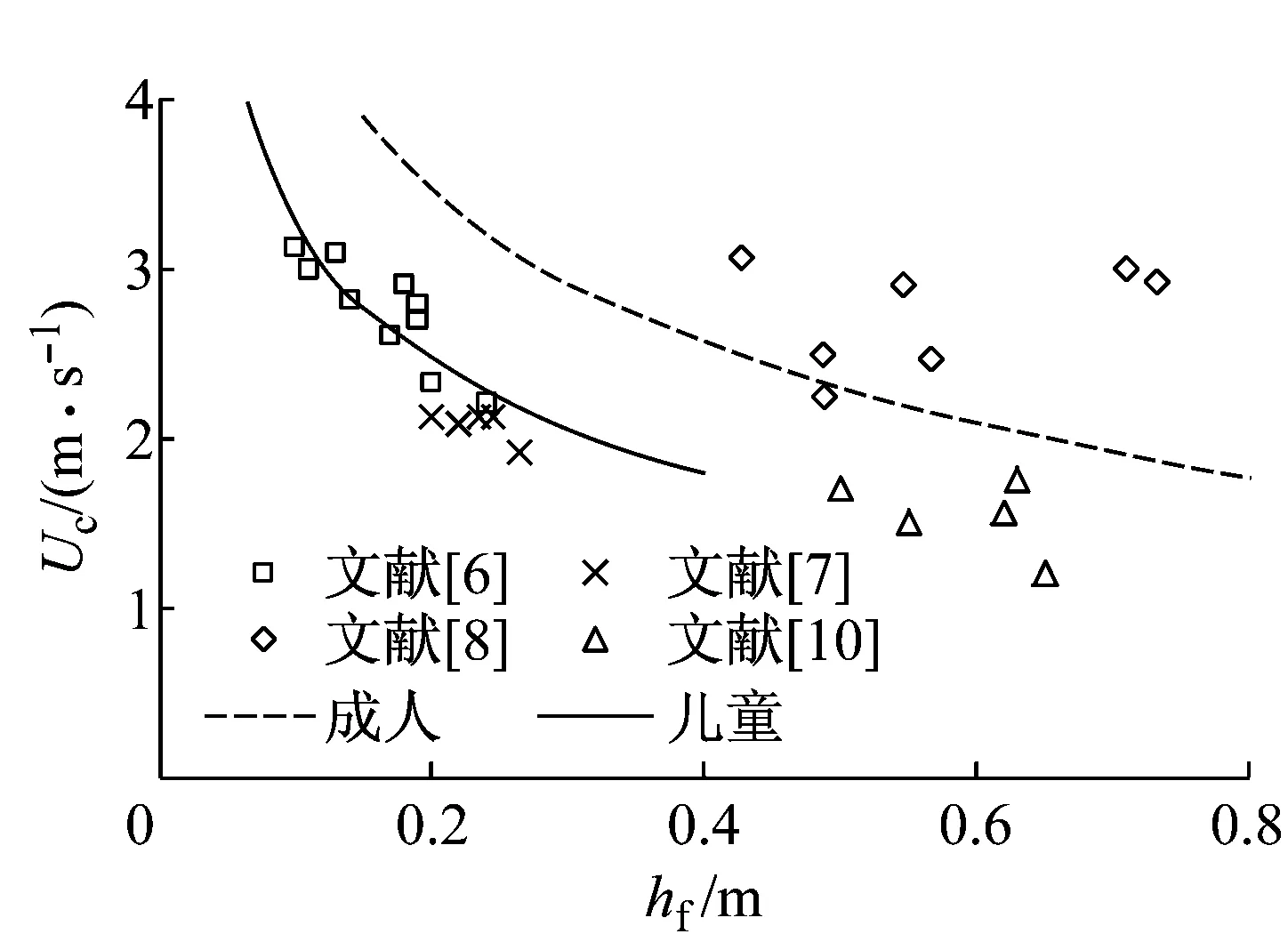
a 滑移失稳

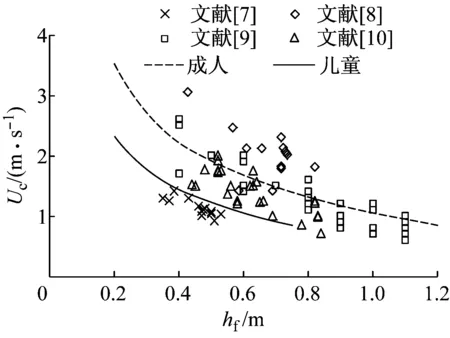
b 跌倒失稳图4　成人及儿童在不同失稳方式下起动流速的计算曲线Fig.4　Comparisons between experimental data for real human bodies including adults and children and calculations using further calibrated formulas at different instability modes

3.3现场试验数据验证

洪水中人体失稳的现场试验数据，包括Jonkman等[11]和Chanson等[12]的研究.Jonkman等[11]通过上游闸门控制天然渠道内的水深及流速进行原型试验，共得到4个失稳数据点，如图5中三角形点所示.Chanson等[12]在真实洪水中测量了三组水流条件，如图5中菱形点所示.其中①点来流条件下测试对象处于安全状态，②和③点处测试对象失去稳定性.利用这些现场试验数据对本文所提出的失稳公式进行验证，分别绘制欧美成人及儿童的跌倒失稳公式计算曲线.参数α，β取表4中的综合前人所有试验数据的率定值，结果如图5所示.图5表明，跌倒失稳公式计算曲线与Jonkman等[11]试验数据相关性较好，而Chanson等[12]的现场实测数据点位于计算曲线的下方.这主要是由于Jonkman等[11]在天然渠道中试验时水流条件良好；Chanson等[12]真实洪水试验中人体稳定性明显低于理论值，这不仅与真实洪水中水流脉动较为剧烈有关，另外测试对象年龄较大也会对试验结果造成一定影响.故基于水槽试验数据率定的参数用于计算真实洪水中人体的失稳条件，结果偏于危险，与上述分析相符.

图5　真实洪水实测数据验证

Fig.5Comparison between experimental data based on field measurement and calculations using derived formulas for adults and children

4　结论

近年来城市洪涝灾害频繁发生，导致人员伤亡严重.已有研究表明，洪水作用下行人很容易失去稳定，被洪水冲走后极有可能导致直接死亡.本文对现有的洪水中人体失稳公式进行改进，得到以下成果：

(1)考虑人体结构沿水深方向的不规则性，利用欧美人体结构的特征参数，修正了不同水深下人体所受的浮力.将已有洪水中人体失稳的水槽试验数据，按不同失稳机制进行划分，重新率定出滑移和跌倒失稳公式中的参数α及β，提出了改进后的洪水中人体失稳标准.

(2)利用已有真实洪水中的试验数据对本文公式进行验证，表明率定后的公式用于预测真实洪水中人体失稳条件时偏于危险.这是由于真实城市洪水中的水流条件较水槽试验条件复杂所致，如水流脉动剧烈、可能挟带漂浮物等.

(3)影响洪水中人体稳定性的因素众多，除水流条件和人体身高体重等特性外，还受测试对象的穿着、地面条件等因素影响.因此今后需进行更多真实洪水中的试验，便于提出适用于不同外界环境时洪水中人体的起动流速公式.

[1]刘春蓁, 占车生, 夏军, 等. 关于气候变化与人类活动对径流影响研究的评述[J]. 水利学报, 2014, 45(4): 379.

LIU Chunzhen, ZHAN Chesheng, XIA Jun,etal. Review on the influences of climate change and human activities on runoff [J]. Journal of Hydraulic Engineering, 2014, 45(4): 379.

[2]胡伟贤, 何文华, 黄国如, 等. 城市雨洪模拟技术研究进展[J]. 水科学进展, 2010, 21(1): 137.

HU Weixian, HE Wenhua, HUANG Guoru,etal. Review of urban storm water simulation techniques[J]. Advances in Water Science, 2010, 21(1): 137.

[3]肖湘. 专家解析我国暴雨致灾根源[J]. 中国减灾, 2012(15): 14.

XIAO Xiang. Analysis of experts on the root of rainfall causing disaster[J]. Disaster Reduction in China, 2012(15): 14.

[4]谭红专. 洪灾的危害及其综合评价模型的研究[D]. 长沙: 中南大学, 2004.

TAN Hongzhuan. Study of hazards associated with flood and its synthetic evaluation model [D]. Changsha: Central South University, 2004.

[5]宋晓猛, 张建云, 王国庆, 等. 变化环境下城市水文学的发展与挑战——Ⅱ. 城市雨洪模拟与管理[J] . 水科学进展, 2014, 25(5): 752.

SONG Xiaomeng, ZHANG Jianyun, WANG Guoqing,etal. Development and challenges of urban hydrology in a changing environment: Ⅱ: Urban stormwater modeling and management [J]. Advances in Water Science, 2014, 25(5): 752.

[6]Foster D N, Cox R J. Stability of children on roads used as floodways[R]. Sydney: Water Research Laboratory, 1973.

[7]Yee M. Human stability in floodways[D]. Sydney: University of New South Wales, 2003.

[8]Abt S R, Wittler R J, Taylor A,etal. Human stability in a high flood hazard zone[J]. Journal of the American Water Resources Association, 1989, 25(4): 881.

[9]Karvonen R A, Hepojoki H K, Huhta H K,etal. The use of physical models in dam-break analysis[R]. Helsinki: Helsinki University of Technology, 2000.

[10]Takahashi S, Endoh K, Muro Z I. Experimental study on people’s safety against overtopping waves on breakwaters[J]. Report on the Port and Harbour Institute, 1992, 34(4): 4.

[11]Jonkman S N, Penning- Rowsell E. Human instability in flood flows[J]. Journal of the American Water Resources Association, 2008, 44(5): 1208.

[12]Chanson H, Brown R, Mclntosh D. Human body stability in floodwaters: The 2011 flood in Brisbane CBD[C]∥5th IAHR international symposium on hydraulic structures. Brisbane: The University of Queensland, 2014: 25-27.

[13]XIA Junqiang, Falconer R A, WANG Yejiang,etal. New criterion for the stability of a human body in floodwaters[J]. Journal of Hydraulic Research, 2014, 52(1): 93.

[14]Cox R J, Shand T D, Blacka M J. Appropriate safety criteria for people[R]. Sydney: Engineers Australia, 2010.

[15]郭青山, 汪元辉. 人机工程学[M]. 天津: 天津大学出版社, 1995.

GUO Qingshan, WANG Yuanhui. Ergonomics[M]. Tianjin: Tianjin University Press, 1995.

[16]Drillis R, Contini R, Bluestein M. Body segment parameters[J]. Artificial Limbs, 1964, 8(1): 44.

Evaluation and Further Improvement of Existing Criteria for Human Stability in Floodwaters

XIA Junqiang1, CHEN Qian1, LI Na2, GUO Peng1

(1. State Key Laboratory of Water Resource and Hydropower Engineering Sciences, Wuhan University, Wuhan 430072, China； 2. China Institute of Water Resources and Hydropower Research, Beijing 100038， China)

There have been numerous urban flood disasters in recent years, causing considerable loss of life. Therefore, the current investigation can provide a scientific basis for flood risk management for people living in urban areas. This paper reviewed previous investigations into human stability in floodwaters. Most of the existing criteria are empirical; other theoretical analyses usually neglect the effects of body buoyance and non-uniform velocity profile of incoming flow, which does not agree with real situations. Although the latest research results have overcome those deficiencies, further improvement is still required because the adopted approach neglects the difference of body structure attributes between the European and Chinese people. Therefore, it is necessary to improve the criterion of human body stability in floodwaters. This paper modified the existing equation of buoyancy force with the parameters of human body structure of Americans or Europeans. Two parameters in the formulas of incipient velocity were re-calibrated based on existing experimental data and an improved criterion for the stability of children and adults in floodwaters was presented. Finally, the proposed formula was validated in detail against existing field experimental data. Because the control conditions for the laboratory experiments were better than those in real floodwaters, the criterion for human stability proposed in this paper tends to be more dangerous in terms of flood risk management.

urban flood; human body stability; formula evaluation; incipient velocity; parameter calibration

2015-04-22

国家自然科学基金(51379156)；水利部公益性行业科研专项经费(201401038)

夏军强(1974—)，男，教授，工学博士，主要研究方向为河流动力学.E-mail：xiajq@whu.edu.cn

X43

A