变压器绕组松动的振动实验分析
李阳海,王广庭,卢双龙,周 淼
(国网湖北省电力公司电力科学研究院,武汉 430077)
变压器绕组松动的振动实验分析
李阳海,王广庭,卢双龙,周淼
(国网湖北省电力公司电力科学研究院,武汉 430077)
变压器绕组故障是变压器故障中的重要部分,基于振动信号分析的方法可以实现变压器绕组运行状态的在线测量。阐述绕组的振动机理及传播路径,通过人为设置绕组松动故障,实测负载时不同松紧程度下的变压器油箱表面的振动信号。利用小波变换(WT)、经验模态分解(EMD)和总体经验模态分解(EEMD)三种方法对信号进行处理,并对信号能量熵求解,对比结果发现:针对绕组振动信号,三种能量熵变化规律与100 Hz处幅值均可作为初步判断绕组松动的指标。
振动与波;变压器;绕组松动;能量熵
变压器是电力系统中最关键的设备之一,它在运行过程中内部可能会出现故障,影响到变压器的正常运行,甚至对整个电力系统造成损坏。因此,为了可以及时发现变压器的故障隐患,避免突发事故,开展变压器状态监测与故障诊断的研究具有十分重要的意义[1]。
变压器绕组松动故障是导致变压器绝缘问题、绕组烧坏等严重故障及事故的主要前期原因。传统的绕组故障诊断方法有短路阻抗法、频响分析法、低压脉冲法和频率响应法等都需要变压器停机才能实现,无法满足在线监测的要求[2-4]。
基于振动分析的监测方法对变压器绕组的机械机构参数的状态和故障反应灵敏,而且可以安全可靠地达到变压器在线状态监测与故障诊断的目的。国内外学者们对通过在线监测变压器油箱表面振动信号来分析判断绕组及铁芯状况的设想做了大量研究[5-7]。
从研究现状来看,振动信号的处理目前并没有形成统一可靠的标准,因此这一方面是目前振动法研究应用的主要问题。
变压器的振动信号为非线性非平稳信号,只从时域和频域进行分析有很大的局限性。本文通过实验,人为制造绕组松动故障,测得不同松紧程度下的绕组振动信号,利用适合于非平稳信号分析的小波变换(Wavelet transform,WT)、经验模态分解(Empirical mode decomposition,EMD)和总体经验模态分解(Ensemble empirical mode decomposition,EEMD)三种方法对绕组振动信号进行处理。通过小波包(wavelet packet decomposition,WP)对时域信号进行降噪处理之后,分别求得小波包能量熵,EMD能量熵以及EEMD能量熵[8-10],对比三种结果发现,能量熵这一指标能够较好地判别绕组运行状态,其中EMD能量熵响应更加灵敏。
1 绕组振动机理及传播
电力变压器的绕组通常是由若干铜线绕制而成的线饼构成,当负载电流通过变压器绕组时,通电绕组在漏磁场的作用下会受到电磁力[11-12]。短路电流达到稳定时,电磁力为
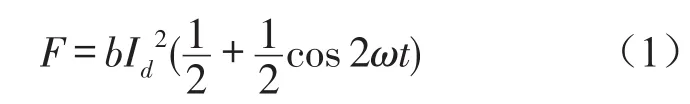
在研究绕组中的动态过程时,可以将绕组视为多自由度振动系统[13]。由于绕组单元数目通常很大,求解较困难,考虑到研究对象是整个线圈在电磁力作用下的运动,各个线圈之间的运动形式差异极小,因此可以认为每个单元的运动规律近似相同,建立整体的振动微分方程

假设绕组压紧力不变,变压器稳定运行时油温变化不大,则刚度K与阻尼系数C均为常数,将(1)代入(2)中求解可得
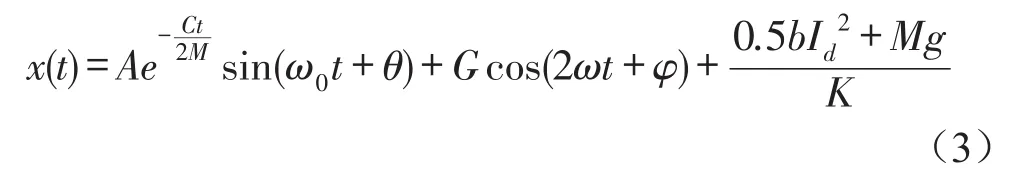
对式(3)求导两次,得到绕组的振动加速度为

式中A和θ的值取决于起始条件的积分常数;φ和G分别为

从结果中可以看出,短路过程中绕组处在由固有振动和强迫振荡所构成的复杂振动之中。绕组的固有振荡频率在很大程度上取决于绝缘垫块刚度K,而K与压紧程度相关,压紧程度越大,K越大,固有频率也越高[14]。上式中前两项为固有振动,经过一段时间之后会衰减,当短路电流达到稳定时,只剩最后一项强迫振动,振动频率为电源频率的2倍,且幅值与负载电流平方成正比。由于电流与磁通之间存在非线性,导致绕组所受电动力中含有高次谐波成分,所以绕组振动加速度信号的频率中还包含高次谐波成分。
2 实验和结果分析
2.1实验及结果
在负载情况下,变压器振动由铁心和绕组共同产生,将低压端短路,高压端施加电压,由于很小的电压就可以使负载电流达到很大,因此铁心的振动可以忽略不计,此时可以认为只有绕组的振动。
实验仪器采用德国m+p数据采集设备和数据分析软件,以及美国CTC三向加速度传感器,测试对象为10 kV油浸式变压器。测点布置如图1所示。
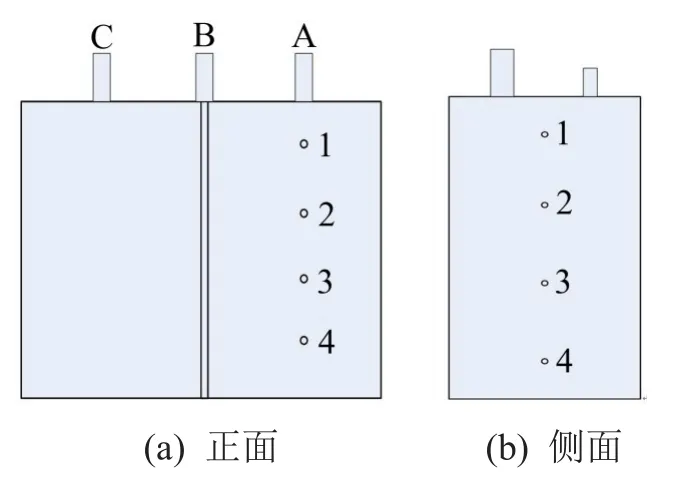
图1 测点布置图
实验过程中测试了短路电流从50%I到100% I(I为额定电流)变化时的振动信号,图2为侧面1号测点的时域图和频谱图。同时作出各个测点振动信号的100 Hz处幅值与负载电流平方的关系图,如图3所示。
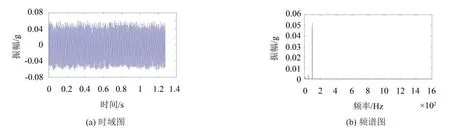
图2 侧面1号测点信号
从图3中可知,各个位置的振动加速度与短路电流平方均为正比关系,因此在一定程度上几个测点数据都可以代表绕组的振动情况。从频谱图中可以看出,绕组振动信号频率集中在100 Hz,高频谐波分量可以忽略。因此首先对比了各个测点在不同松紧程度下100 Hz处的振动幅值。

图3 侧面振动与电流平方关系
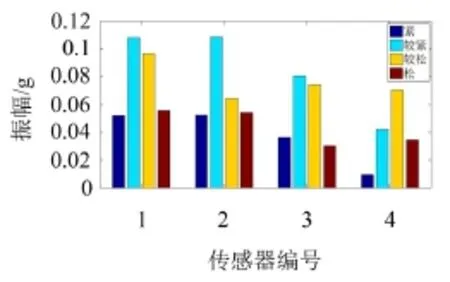
图4 侧面100 Hz幅值
通过图中对比可以看出,随着压紧力减小,各点100 Hz处的幅值先增大后减小。
由式(4)可得稳定后绕组振动加速度为

随着绕组压紧力的减小,绝缘垫块的初始压缩量减少,K的值也将减小。此时有两种情况,当K<4 Mω2时,绕组松动,K减小,G也减小,即振幅减小;当K>4 Mω2时,K减小,G先增大后减小,即振幅先增大后减小。实验结果与理论相符。
2.2数据处理与分析
小波变换、经验模态分解和总体经验模态分解是近年来常被用来对信号进行时频处理并提取特征的方法[15]。
小波变换是一种窗口大小固定不变而其时频窗可以改变的时频局部化分析方法。每次小波分解得到的低频逼近信号和高频细节信号平分被分解信号的频带,二者带宽相等。
Norden E.Huang等人提出任何信号都是由一些不同的基本模式分量(IMF)组成的,而EMD方法可以将信号的基本模式分量提取出来。EMD无需选取基函数,可自适应将信号分解到不同频段中。
EEMD是为了解决EMD存在的边缘效应、模态混叠等不足,在EMD基础上改进而来的一种方法,原理是利用了白噪声的均匀分布的统计特性,在信号中加入白噪声,使信号在不同尺度上具有连续性。
分别利用三种方法对变压器表面测得的绕组振动信号进行了分析,其中小波基函数选取dmey,之后分别得到分解结果的时域重构图及对应频谱图。其中,EEMD方法中,当添加的白噪声标准差太大时,会分解出额外的噪声分量,因此将其设置为0.01,为了计算效率将噪声添加次数设为50。限于篇幅,图中EMD和EEMD分解结果只选取了前五个IMF。
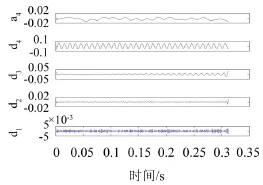
图5 小波分解结果
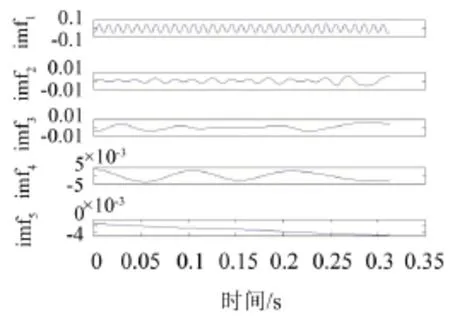
图6 EMD分解结果

图7 EEMD分解结果
对比三种方法的时频分解结果可知:小波分解结果与小波基的选取有很大关系,dmey小波可以较好地提取信号不同频段的特征;EMD分解没有得到100 Hz以上的高频部分,但由于绕组振动信号频率较为单一,并没有出现边缘效应及模态混叠;EEMD较全面地得到了信号各频段信息,不足之处在于运算时间会随噪声添加次数近似线性增长。
2.3能量熵对比
当绕组状态发生变化时,振动信号在不同频段的能量分布会发生相应的变化。因此可以引入能量熵来对绕组状态进行判断。能量熵是反映信号能量分布的混乱程度。根据Shannon信息熵的含义,此处能量熵HEN定义为[16]

其中pi=Ei/E,对于小波分解结果而言是每层高频细节信号和最后一层低频逼近信号中第i个频段能量占总体能量的比例;对于EMD及EEMD而言是第i个IMF的能量分布。
通过上述方法进行计算,得到绕组在不同压紧力下三种能量熵。结果如表1、表2所示。
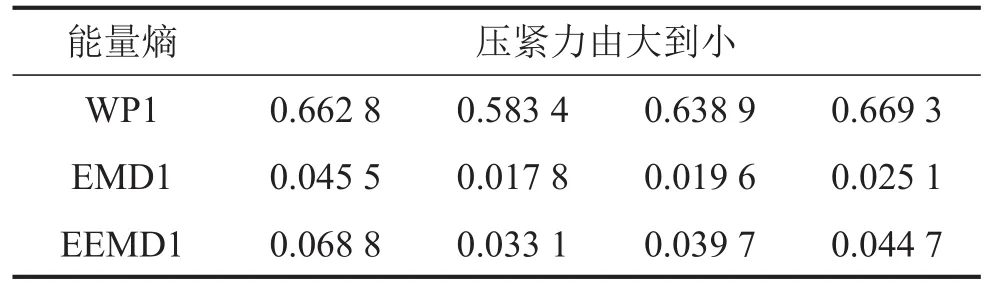
表1 侧面Z1能量熵
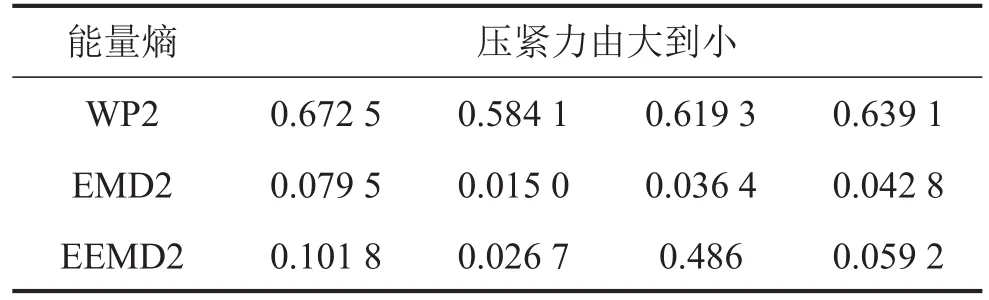
表2 侧面Z2能量熵
对比表中数据,随着压紧力的减小三种方法所得能量熵均是先减小后增大,其变化规律与100 Hz处幅值变化有一定联系。为了直观地观察能量熵的变化幅度,将表中数据作图8,可以发现EMD能量熵和EEMD能量熵变化程度相当,对绕组松动的响应较为灵敏。

图8 能量熵变化情况
根据能量熵的定义,HEN随着pi的增大呈先增大后减小的趋势,因此能量分布越平均,能量熵值越大,反之则能量熵越小。变压器绕组的振动信号100 Hz频率分量占绝对优势,因此当绕组开始出现松动,100 Hz分量的幅值增加时,其能量比例,即pi也会增加,因而能量分布更为集中,能量熵减小;而继续松动到K<4 Mω2后,100 Hz分量减小,能量熵相应地出现增大现象。
实验过程中由于调节压紧力的变动范围较大,使K的变化越过了临界点K=4 Mω2,能量熵经历了先减小后增大的过程。而在实际运行中,压紧力不会突然出现较大的变化,K通常会保持在4 Mω2以上,当监测到振幅增加、能量熵减小时,便能够判断绕组出现了松动,需要及时采取措施修复故障。
3 结语
通过人为设置变压器绕组松动故障的实验,测得不同松紧程度下的油箱表面振动信号,对信号的处理分析得到以下结论。
(1)绕组振动信号频率集中在100 Hz处,高频分量可以忽略。对比各点信号100 Hz频率分量处的幅值发现,振幅随着压紧力的减小,先增大后减小,结果符合理论分析结果。
(2)利用针对非线性非平稳信号的小波变换、EMD和EEMD等方法对信号进行了处理,处理结果显示小波变换与小波基的选取有很大关系,且由于振动频率单一,EMD并没有出现模态混叠,EEMD分解效果良好,避免了潜在的模态混叠,只是计算时间稍长。
(3)通过对比三种方法计算得到的能量熵,发现当绕组出现松动故障时,能量熵的变化与100 Hz处幅值的变化呈现恰好相反的规律。在实际运行中,绕组垫块刚度K>4 Mω2,压紧力小幅减小时,振幅增加,能量熵减小,二者均可用来对绕组是否松动作出初步判断,其中EMD和EEMD能量熵的变化更明显,为避免潜在的模态混叠,EEMD方法更加可靠。
[1]王世阁,钟洪璧.电力变压器故障分析与技术改进[M].北京:中国电力出版社,2004.
[2]DICK E P,ERVEN C C,Transformer diagnosis testing by frequency responseanalysis[J].IEEE Trans PAS-97,1978(6):2144-2152.
[3]LECH W,TYMINSKI L.Detecting transformer winding damage-the low voltage impulse method[J].Electrical Review,1966.10:768-772.
[4]王钰,李彦明,张成良.变压器绕组变形检测的LVI法和FRA法的比较研究[J].高电压技术,1997,23(1):13-15.
[5]BERLER Z,GOLUBEV A.Vibra-acoustic of transformer clamping pressure monitoring[C].Conference Record of the 2000 IEEE International Symposium on Electrical Insulation,Anaheim,CAUSA,April 2-5,2000.
[6]GARCIA B,BURGOS J C,ALONSO A M.Transformers tank vibration modelling as a method of detecting winding deformations-partI:theoreticalverification[J].IEEE Trans PD,2006,Volume 21:164-169.
[7]GARCIA B,BURGOS J C,ALONSO A M.Transformers tank vibration modelling as a method of detecting winding deformations-part II:experimental verification[J].IEEE Trans PD,2006,Volume 21:164-169.
[8]汲胜昌,刘味果,单平,等.小波包分析在振动法监测变压器铁心及绕组状况中的应用[J].中国电机工程学报,2001,21(12):25-27.
[9]臧状,陈江波,李辉,等.EEMD能量熵在配电变压器绕组状态监测中的应用[J].高压电器,2015,51(11):187-193.
[10]熊卫华,赵光宙.基于希尔伯特-黄变换的变压器铁心振动特性分析[J].电工技术学报,2006,21(8):9-13.
[11]谢书明,唐任远.大型电力变压器漏磁场分析与计算[J].沈阳工业大学学报,1994,16(1):18-22.
[12]KLADAS A G,PAPADOPOULOS M P,TEGOPOULOS J.Leakagefluxandforcecalculationonpower transformer windings under short-circuit:2D and 3D models based on the theory of images and the finite elementmethodcomparedtomeasurements[J]. Magnetics,IEEE Transactions,1994,30(5):3487-3490.
[13]BASTARDP,BERTRANDP,MEUNIERM.A transformer model for winding fault studies[J].Power Delivery,IEEE Transactions,1994,9(2):690-699.
[14]邵宇鹰,饶柱石,谢坡岸,等.预紧力对变压器绕组固有频率的影响[J].噪声与振动控制,2006,26(6):51-53.
[15]何正嘉,訾艳阳,张西宁.现代信号处理技术及应用[M].2006.
[16]YU Y,JUNSHENG C.A roller bearing fault diagnosis method based on EMD energy entropy and ANN[J]. Journal of Sound and Vibration,2006,294(1):269-277.
Experimental Research of Transformer’s Vibration due to the Winding Looseness
LL Yang-hai,WANG Guang-ting,LU Shuang-long,ZHOUMiao
(State Grid Hubei Electric Power Testing and Research Institute,Wuhan 430077,China)
The winding fault is an important part of transformer faults.Analysis of vibration signal can realize online monitoring of the winding operation.In this paper,the vibration mechanism of winding and the propagation path of vibration are introduced.By making the winding faults artificially,vibration signals of the oil tank surface of the transformer are measured under different winding looseness.These signals are processed with wavelet transform(WT),empirical mode decomposition(EMD)and ensemble empirical mode decomposition(EEMD).And the energy entropies of the three methods are also calculated.Comparison of the results shows that both variation laws of three kinds of energy entropy and the amplitude at 100Hz can be used as the criteria for preliminary estimation of the looseness of the winding.
vibration and wave;tarnsformer;winding looseness;vibration;energy entropy
TM3
ADOI编码:10.3969/j.issn.1006-1335.2016.05.008
1006-1355(2016)05-0034-04+55
2016-05-27
李阳海(1980-),男,重庆市人,博士生,主要研究方向为汽轮机热力性能试验及机网协调试验等研究工作。E-mail:45629450@qq.com

