混凝土的徐变恢复及其计算的数学模型

余伦明 王雷

摘 要：混凝土的徐变恢复，对于准确地预测可变应力作用下的高墩大跨连续刚构桥的徐变效应及阐明徐变的产生和发展机理具有重要的意义。本文提出基于双功能函数的混凝土徐变数学模型，可供广大工程技术人员参考。

关键词：混凝土；徐变恢复；数学模型；双功能函数

1.概述

高墩大跨连续刚构桥广泛采用悬臂挂篮浇筑的施工方法，结构体系的转换会对上部结构梁段的受力产生巨大的影响，T梁悬臂浇筑时刻与边跨合龙后及中跨合龙前的梁段的受力完全不同。因此在桥梁施工至合龙前的施工期内，梁单元截面的内力随时间呈现出不同的大小及拉压状态。混凝土的徐变恢复对于准确地预测可变应力作用下的高墩大跨连续刚构桥的徐变效应及阐明徐变的产生和发展机理具有重要的意义。

2.徐变恢复数学模型

由于应用线性叠加原理，把荷载减小或去除下的徐变恢复，简单地采用当量正荷载在相同加载及计算龄期下所引起的大小相等而方向相反的徐变效应来叠加，会带来较大的误差。一个重要的原因是混凝土的徐变不仅与当前应力有关，而且与应力历史有关，受荷载长期作用的混凝土构件，卸载后其徐变恢复明显地小于线性叠加原理的计算结果。也就是说，在应力减小的情况下，徐变恢复使得徐变应变与应力之间不再呈现线性关系，这种非线性关系归咎于构件卸载前的受压预载。因此对于卸载或减载下的徐变预测模型，有必要将徐变和徐变恢复作为两个不同的方面来考虑，即采用双功能函数的方法，将应力减小下的徐变模型通过一个持续荷载作用下的线性徐变模型和一个卸载情况下的徐变恢复模型来表示。

按照线性徐变叠加原理，在阶段可变应力作用下的应力-应变关系为：

上式中， 为 时刻的应变，包括初始应变和徐变应变； 为徐变函数； 为时段加载初期的应力； 为对应于时间刻度 的增量段应力增量。从（1）式可以看出，视应力减小（卸载）为增加一个负应力增量。也就是说，徐变恢复被当做一个负的反号徐变来处理。图1给出了应用线性叠加原理在卸载下的徐变应变时效图。与试验资料相比，应用公式（1）求出的应力减小状态下的徐变恢复显然被高估。

混凝土的徐变恢复应变与卸载前的常应力成正比，单位应力的徐变恢复称为弹性后效。在图1中，荷载进程分成了两个阶段，即在 时段的应力常量 和在 时段的减小的应力 ，显然卸载或部分去除的应力 引起了徐变恢复。按照上面介绍的双功能函数表示法，假如徐变函数 和徐变恢复函数 已知，则有下面的变形响应：

式（4）即为基于双功能函数的阶段可变应力作用下的应力-应变关系。上式可以延伸推广到更复杂的可变应力历史的情形，但需要记录阶段荷载的应力历史，详细的讨论及推导在初应变法的收缩徐变分析中作进一步介绍。

文献[1]基于CEB-FIP（MC90）模式给出了徐变函数如下：

为最优化参数，RH为环境相对湿度， 为名义厚度， 为混凝土的平均抗压强度。

上式中， 称之为徐变恢复终值， 称为徐变恢复随时间的发展系数，其各自的表达式为：

3.实验数据对比分析

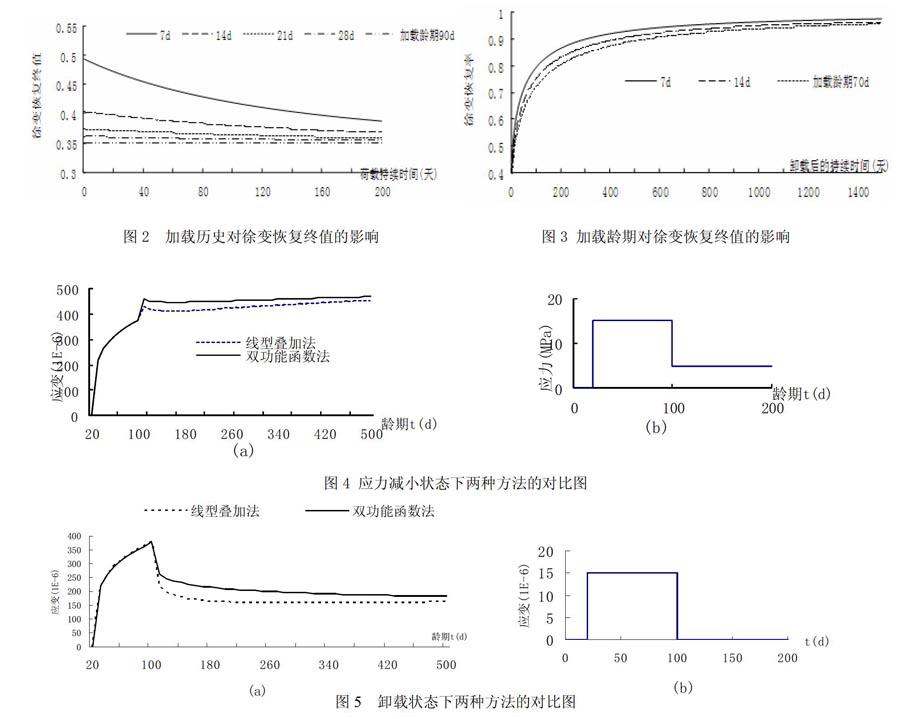
根据本文的双功能函数模型，及公式（1）～（2-11）的表达给出了应力减小状态下徐变恢复的相关响应。图2反映了徐变恢复终值与加载历史的关系，徐变的恢复随加载龄期而变化，当加载较早、荷载持续较短时，双功能模型反映了快速发展的徐变恢复，而后期加载（加载龄期在三个月后）其徐变恢复较小，且趋于稳定。图3反映了加载龄期对随时间发展的徐变恢复的影响，这与试验数据能够很好地匹配。

应力减小情况下的双功能函数表示方法，与试验数据之间有着很好的拟合度。图4、图5给出了按照线性叠加原理的等式（1）与按照等式（3）、（4）的双功能模型计算的徐变柔度的比较图。从图中可以看出，应用简单的线性叠加原理总的来说较大地高估了徐变恢复。

4.结束语

本文提出基于双功能函数的混凝土徐变数学模型，从理论上考虑了混凝土的徐变恢复，实验数据证明，本文方法对于准确地预测可变应力作用下的高墩大跨连续刚构桥的徐变效应及阐明徐变的产生和发展机理具有重要的意义，可供广大工程技术人员参考。

参考文献

[1] L.L.Yue， L.Taerwe. Two-function method for the predication of concrete creep under decreasing stress，Materials and Structures， 1993，25：268-273

[2] L.L.Yue， L.Taerwe. Creep recovery of plain concrete and its mathematical modelling，Magazine of Concrete Research，1992，44（161）：281-290

[3] 高政国，赵国藩. 混凝土徐变分析的双功能函数表达式，建筑材料学报，2000-9，4（3）：250-254

[4] 刘德宝，郑信光. 徐变系数计算的应用研究，同济大学学报，1998-10，26（5）：533-536

[5] 铁道部专业设计院桥隧处，杜士杰. 收缩、徐变理论在工程设计中的应用，铁道设计标准，1998，6：14-15

[6] 中国建筑科学研究院结构所规范室译. 验证文选集（90年CEB-FIP模式规范应用指南）：混凝土结构，北京：中国建筑科学研究院， 1993-04，28