运动控制在变桨控制系统中的应用

缪新磊，　秦栋平

福氏新能源技术(上海)有限公司　上海　201203



运动控制在变桨控制系统中的应用

缪新磊，秦栋平

福氏新能源技术(上海)有限公司上海201203

风力发电变桨控制系统本质上是一个运动控制系统,运动控制系统的跟随误差、定位时间和定位误差会影响变桨的性能,从而影响发电机的输出功率。从运动控制角度出发，分析了单轴变桨系统的数学模型，在原有PID控制器基础上引入速度前馈和加速度前馈，并用MATLAB软件进行了仿真验证。在某风机的实际应用中，仿真代码导入控制器，结果显示引入的前馈控制器可有效提高发电机输出功率的平稳性。

运动控制; 前馈; 控制器; 发电

作为自动控制的重要分支，运动控制技术[1]在很多领域大显身手，应用及其广泛，例如军事和宇航方面的雷达天线、火炮瞄准、惯性导航、卫星姿态，以及飞船光电池板对太阳跟踪的控制等。工业方面的各种加工中心、注塑机、数控机床、工业机器人、风力发电机等也要用到运动控制。

运动控制就是通过机械传动装置对运动部件的位置、速度进行实时控制管理,使运动部件按照预期的轨迹和规定的运动参数(如速度、加速度参数等)完成相应的动作。运动控制系统由于能够实现对运动轨迹、运行速度、定位精度及重复定位精度的精确控制，所以在以上所述各类控制工程中有着广泛应用。

一个狭义的运动控制系统包括运动控制器、伺服驱动器、交流伺服电机、反馈装置、机械传动机构和负载等[2]。运动控制系统快速精确的响应可以极大地提高驱动系统的性能，但与此同时，位置偏差及速度波动存在于很多机电系统的应用中，如风力发电变桨控制系统。

出于简化理论分析的需要，风力发电变桨控制系统可以用两惯性模型进行描述。在经典的两惯性控制问题中，通常假设只有驱动侧的速度反馈信号，而驱动力矩、负载侧的速度反馈和扰动力矩均不可测量，因此要求设计的控制器在仅使用驱动侧速度反馈的前提下，能够对负载侧进行有效地速度控制和位置控制。在风力发电系统中，如果能在变桨过程中降低位置偏差和速度波动，将会有效减小发电机功率输出的波动，并减小对电网的冲击。

该经典控制问题有一些解决方案，如基于极点配置的PI/PID控制器、基于状态反馈的两自由度控制结构等[3]。此外，众所周知，低阶的PID控制器及其变形在运动控制系统中具有压倒性的普及率，继续改善包括PID控制器在内的低阶控制器设计无论在理论上还是在实际中都有着重要的意义。

笔者建立了电机与负载的模型，在原有PID控制器基础上加入了速度前馈和加速度前馈[4]，有效降低了机械振动和跟随误差，使风力发电系统能够平稳地输出功率。

1　变桨控制系统的运动控制模型

变桨系统中每个桨叶采用一个单独的带旋变反馈的伺服电机[5]，驱动机械传动机构进行调节。具体而言,伺服电机由减速箱通过主动齿轮与桨叶轮毂内齿圈相连，带动桨叶进行转动，实现桨叶的桨距角控制。在轮毂内齿圈的边上再安装一个SSI编码器，直接检测内圈转动的角度，即桨叶桨距角变化，但这一参数不用作运算，即系统实际上是半闭环控制。

1.1单轴运动控制模型

变桨伺服控制系统可以简单理解为三个单独轴的点位运动，其核心控制思想为单轴的运动控制。单轴的两惯性电机与负载模型如图1所示。

图1　电机与负载模型

图中KML为传动机构的弹性系数，DML为传动机构的黏性摩擦因数，VM为电机速度，VL为负载速度，TML为力矩。根据图1可以得出下式：

(1)

式中：1/s为积分环节。

(2)

(3)

式中：ωr为共振频率；ωα为反共振频率；ζr为阻尼比；J为转动惯量；GTM(s)和GTL(s)为传递函数。

出于一般性讨论的目的，用s*=s/ωα替换s[6]，方程可以正规化为：

(4)

式(4)中q可以定义为惯性比，即驱动侧惯性Jm与两惯性系统全体惯性(Jm+Jl)的比值：

(5)

如图2所示，随着惯性比q的增大，共振频率和反共振频率会趋于接近，即倾向于零极点抵消。而零极点抵消会导致系统鲁棒性的降低，同时共振频率降低会导致控制系统需要提供更强的阻尼，从而会牺牲系统的稳定裕度和带宽，所以两惯性系统控制器的设计难度直接由惯性比q的大小决定。

图2　正规化两惯性模型的伯德幅值图

1.2变桨系统数学模型

风力变桨系统[7]由变桨控制器、变桨电机、传动系统、风机桨叶构成。根据变桨电机、传动系统和风机桨叶的力矩平衡关系，得到变桨系统数学模型：

(6)

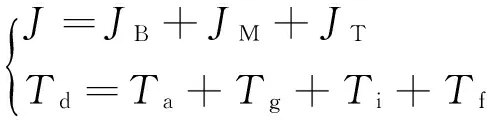
式中：J为折算到电机轴的变桨系统转动惯量，包括变桨电机的转动惯量JM、折算后传动系统的转动惯量JT、折算后风机桨叶的转动惯量JB；ω为变桨电机转速；b为与变桨转速有关的阻尼系数；Td为折算至电机轴的变桨系统扰动力矩,包括折算后的气动负载Ta、重力负载Tg、惯性负载Ti和摩擦负载Tf扰动力矩；TM为变桨电机的输出力矩。

对于运动控制而言，惯量匹配是一项非常重要的特性需求，而对于驱动器而言，良好的惯量匹配才能产生良好的动态性能。在理想的刚性连接情况下，仅需计算出所需扭矩，即可驱动系统，并使其处于高动态特性运转状态。然而，由于机械系统(例如减速机、皮带、联轴器等)的连接具有弹性变形，无法实现真正意义上的高动态控制特性，这就带来了惯量匹配问题[8]。在驱动器对负载的控制过程中，电流环的计算周期非常短，在惯量匹配值较大的情况下，系统需要给出一个非常大的偏差才能在PID调节中实现输出，当然，此时这一输出的扭矩会产生较大的振动。

2　前馈的引入

风力机主控系统结合当前风速、发电机功率等状态数据,下发桨叶节距角位置指令。变桨系统实时响应主控指令，驱动桨叶达到指定角度位置。为避免风速变化引起的大型风力发电机输出功率波动，系统在超过或低于额定风速下运转时，主动调节桨叶的节距角，改变传送到传动轴的转矩，从而使运行满足恒转矩和恒功率[9]。

在风力发电系统中，伺服系统的定位时间、定位误差及跟随误差是需要控制的几个参数。变桨系统需要实时响应主控发来的位置指令，在最短的时间内运动到指令位置，以满足功率输出的需要。跟随误差与运动速度相关，一般而言，速度越大，跟随误差越大，如果在位置环加入速度前馈，可以有效减小高速运动中的误差，降低对电网的冲击。速度前馈一般是实际反馈速度相乘一个比例值，并将所得加到由位置环PID运算出的速度指令上。

速度前馈的引入有效减小了位置跟随误差，但加减速阶段的位置跟随有些偏大。此时在速度前馈的基础上，引入加速度前馈，这一附加值输出给驱动器，驱动器在电流环计算中预先给出电流值，即可实现前馈控制。这一附加值是通过系统不断计算，以微秒级的周期循环并提供给驱动器电流环的。当速度前馈和加速度前馈给出后，根据当前值和机械常数计算出整个运动过程的惯量变化，并计算出力矩输出的前馈值给电机。这一前馈值与控制器给定值在电流环中的控制输出进行叠加，使扭矩输出可以快速实现稳态调整，从而减小扭矩输出的偏差。

经MATLAB/Simulink仿真工具[10]建模生成的控制器模型可以自动生成技术产生控制器的C代码，这一代码无需手工重写即可载入DEIF AWC400控制器中，应用于实际风电项目。

3　试验结论

为了获得足够的数据，笔者采用DEIF变桨控制系统，将AWC400作为变桨系统的控制器，IMD122A作为变桨伺服电机驱动器，在国内某知名风电公司风力发电机组上作了试验。

图3为控制器中引入前馈控制策略后,在发电状态下从主控数据缓冲区读取的指令位置与变桨实际位置的偏差，以及功率的对比。图中横坐标为时间(s)，左侧纵坐标为功率(kW),右侧纵坐标为偏差角度(°)。

图3　偏差与功率对比

速度前馈和加速度前馈的引入在很大程度上减小了位置跟随偏差，速度波动也随之减小。位置偏差如果能稳定在0.4°内，发电量将很平稳；如果有超过0.4°的区间，发电量将波动异常。

风机如果能保证在风速变化很剧烈的情况下稳定输出功率，将能有效减小对电网的冲击。变桨位置跟随偏差不是影响发电量的唯一因素，但却不可忽略。变桨运动控制系统采用哪种控制策略将直接决定自身性能，由于变桨系统传动机构采用减速器及齿轮传动，可以把变桨系统看成是弹性系统及非线性系统，前馈控制策略并不是专门针对非线性系统设计的，新的控制策略(如多项式控制策略)已在进一步研究之中。

[1] 朱小莉.基于DSP技术的运动控制卡的研究与开发[D].武汉： 华中科技大学，2007.

[2] 汪海波,田炜,鲁斌,等.兆瓦级风电机组电动变桨距系统测试平台设计[J].电力系统自动化,2010,34(24)： 74-77.

[3] 宿敬亚，樊鹏辉，蔡开元.四旋翼飞行器的非线性PID姿态控制[J].北京航空航天大学学报，2011，37(9)： 1054-1058.

[4] 杨辉，吴钦章，范永坤，等.加速度前馈在高精度伺服跟踪系统中的应用研究[J].光电技术应用，2007，22(6)： 48-51.

[5] 陈远，樊亚东，江政，等.小型永磁同步电机温度场分析中几个关键问题的解决方法[J].上海电气技术，2009，2(3)： 50-52.

[6] MA C B, CAO J Y, QIAO Y. Polynomial-method-based Design of Low-order Controllers for Tow-mass Systems[J]. IEEE Transactions on Industrial Electronics, 2013,60(3): 969-978.

[7] 禹华军.风力发电机组中的振动监测与分析[J].装备机械，2011(3)： 52-56.

[8] 宋华振.浅述贝加莱机器人控制中的惯量前馈控制技术[J].伺服控制,2011(8)： 91-92.

[9] 叶成城.兆瓦级风电机组电动变桨距控制系统的研究与实现[D].上海： 上海交通大学,2013.

[10] 陈永刚，刘大勇，阎秋生.基于PMAC的直线电机高定位增益前馈PID控制算法研究[J].机械制造，2013，51(12)： 35-37.

Wind turbine pitch control system is essentially a motion control system, the following error, positioning time and positioning errors of the motion control system can affect the performance of the pitch, thereby, it may affect the output power of the generator. From the perspective of the motion control, the mathematical model of the uniaxial pitch system was analyzed and the velocity feedforward and acceleration feedforward were introduced on the base of the original PID controller. It was demonstrated via the simulation by MATLAB software. In practical blower fan applications, the simulation code was led into the controller. The results show that the lead-in feedforward controller could effectively improve the smoothness of the generated output power.

Motion Control; Feedforward; Controller; Power Generation

2015年10月

缪新磊(1987—)，男，硕士，助理工程师，主要从事变桨控制系统工作，

E-mail： smi@deif.cn

TM614

B

1674-540X(2016)02-049-04