热荷载与风荷载作用下点式支承玻璃的破裂行为规律

赵 寒,王 禹,王青松,陈昊东,孙金华

(中国科学技术大学火灾科学国家重点实验室，合肥，230026)



热荷载与风荷载作用下点式支承玻璃的破裂行为规律

赵 寒,王 禹,王青松*,陈昊东,孙金华

(中国科学技术大学火灾科学国家重点实验室，合肥，230026)

在高层建筑火灾中，玻璃幕墙的破裂受到环境风和室内火灾的共同影响。研究了600 mm× 600 mm × 6 mm的浮法玻璃幕墙在点支承安装方式下受到热辐射荷载和风荷载情况下的响应规律。分析了不同工况下玻璃表面的温度变化、风荷载的大小与玻璃破裂时间的关系、玻璃破裂与温差之间的关系、玻璃裂纹扩展及其与风速之间的关系。结果表明在玻璃两侧分别受到热辐射和风荷载共同作用时，风荷载的增加会加速玻璃的破裂。研究结果可为玻璃幕墙的工程应用提供技术支撑。

点支承玻璃; 热荷载; 风荷载; 首次破裂时间

0 引言

随着社会的发展，人们对生活和工作环境的要求越来越高。玻璃由于其美观，经济和良好的透光性越来越广泛地应用到现代高层建筑中。但是它在给人们带来舒适生活的同时，也带来很大的安全困扰。一旦发生高层建筑室内火灾，玻璃受到热荷载的作用发生破裂就会形成通风口，大量的室外空气进入室内会加大火势，同时破裂的玻璃散落在地面，也给应急救援带来困难。当发生高层室内火灾时，玻璃一方面受到来自室内热荷载的作用，另一方面要受到环境风的作用。因此研究风荷载和热荷载双重作用下玻璃的破裂行为就显得尤为重要[1]。

Griffith理论[2]认为玻璃等脆性材料内部存在着众多微小裂纹或缺陷，当受到外力时这些缺陷或裂纹就会发生应力集中的现象，当应力集中到一定程度裂纹便开始扩展继而导致断裂。在热荷载对玻璃的影响方面，有许多学者通过实验和模拟的方法来研究玻璃的破裂行为。Emmons[3]首先提出了建筑中的这一结构问题。Keski-Rahkonen[4]经过大量的研究提出了温差判据公式：

(1)

其中σb是玻璃内部的热应力，E 是杨氏模量， β 是玻璃的线性膨胀系数，ΔT 是温差。Skelly等[5]做了四边遮蔽和不遮蔽的对比试验发现玻璃所能承受的最大玻璃中心与边缘的温差是90℃。Joshi和Pagni[6]和Wang等[7]利用威布尔分布分析了玻璃破裂的概率问题。Wang等[8]从实验和模拟两方面探究了点支承安装方式下玻璃的破裂行为，认为玻璃上打孔的位置与玻璃的破裂时间也存在一定关系。也有许多学者对风荷载对玻璃破裂行为的影响进行研究。Brown[9]认为风荷载对玻璃的影响要依赖于应力在时间维度上的积累，提出了布朗效应。在布朗效应的基础上，Gavanski和Kopp[10]从实验上验证了这一定律。

尽管前人进行了大量的关于玻璃破裂的研究，但在风荷载和热荷载双重作用下破裂特性方面的研究仍很不足，而在本研究的预实验中发现风荷载或热荷载单独作用与共同作用有明显的不同。因此，本实验将探究风荷载和热荷载双重作用下玻璃的破裂行为规律。

1 实验设计

实验装置由热辐射源、玻璃、玻璃支架、安装热辐射源和玻璃的箱体、风机以及测量系统组成，如图1所示。测量系统包括有10个贴片式热电偶、1个铠装式热电偶及数据采集仪。实验采用了工程上用的600 mm× 600 mm × 6 mm的浮法玻璃，玻璃的四边均做磨边处理。其中玻璃中心距地面的高度是800 mm。组合箱体下表面距地面为300 mm。而摄像机放置在与玻璃中心同一等高线上，且位于玻璃的一侧，记录玻璃破裂的过程。热辐射源距玻璃热荷载一侧表面为900 mm。设定热辐射源的加热功率是90 kW。本文确定风速的方法是：在玻璃表面选取9个点，如图2所示，计算其平均风速作为作用在玻璃表面的风速。通过前期的预实验，不断迭代风速，最终确定实验所需要的频率。

图1 点式支承玻璃破裂实验简图Fig.1 The schematic of experiment

图2 风速测点分布图Fig.2 The distribution of measuring points of wind speed

图3 玻璃与玻璃框架的连接方式Fig.3 The connection of glass and frame

本实验采用点支承的玻璃安装方式，玻璃与玻璃框架的连接方式如图3所示。玻璃与玻璃框架的连接，每一个孔有一个螺栓和两个螺母来完成固定，玻璃上有A，B，C，D四个孔，因此为了使得玻璃能够安装牢固，每一组实验都需要8个螺母。每一个孔的孔径为10 mm，孔径中心距最近的玻璃边缘为35 mm。

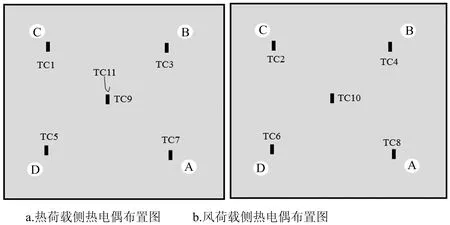
图4 点式支撑安装方式玻璃表面热电偶分布Fig.4 The distribution of thermocouples in the glass surface

热电偶的布置如图4所示。TC1，TC3，TC5，TC7，TC9布置在热荷载的一侧，直接测量热辐射源一侧玻璃表面的温度。TC2，TC4，TC6，TC8，TC10布置在风荷载的一侧，直接测量风荷载一侧玻璃表面的温度。TC11测量玻璃热辐射源一侧中心点附近的温度。热电偶TCi测量的温度用Ti表示。TC1～TC10位于孔径周围且距孔径中心15 mm(如图4所示)。为了保证实验时箱体的密封性，玻璃安装在一个玻璃框架的槽内。则本实验定义3种温差：

温差ΔT1公式为：

(2)

温差ΔT2公式为：

(3)

其中，Tmax是破裂时刻玻璃表面的最大温度，Tmin是破裂时刻玻璃表面的最小温度。

温差ΔT公式为：

(4)

本实验研究在热荷载不变的情况下，改变玻璃另一侧的风速，研究其对玻璃破裂行为的影响。实验台搭建完成后对浮法玻璃一共进行了12组实验，可依次标记为4个工况，分别按照0m/s、2m/s、5m/s、8m/s来改变施加在玻璃风载荷侧的风速。实验工况详见表1。为了保证实验结果的可靠性，每种工况做三组实验。本文使用的玻璃的相关力学和光学参数如下：密度ρ=2360 kg/m3，弹性模量E=61.6MPa， 泊松比v=0.22，韦氏硬度Hv=5.99 GPa，可见光透射率τv=0.77，传热系数U=5.70 W/(m2·℃)。

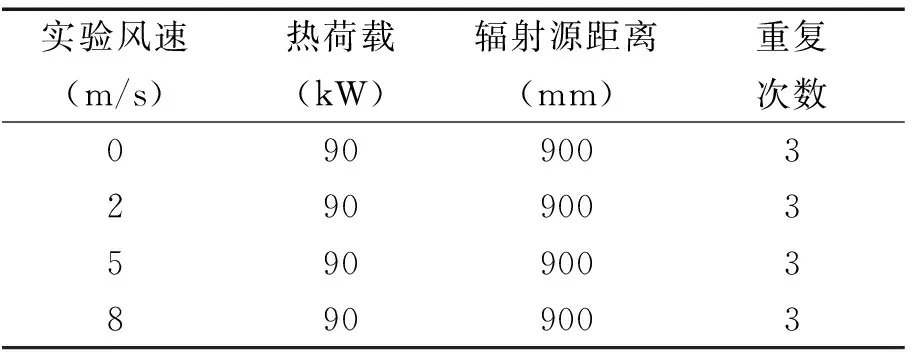
表1 实验工况概述

实验采用了单一变量的科学方法来研究玻璃的破裂行为，保持对玻璃的加热功率和热辐射源与玻璃表面的距离不变，通过改变风速的大小来控制实验的条件。

2 实验结果的分析讨论

由表2可以看出，所有玻璃在实验中全部发生起裂。在无风状态下玻璃发生起裂的位置全部在玻璃表面的打孔处，而有风状态下，有3组实验玻璃的起裂位置发生在玻璃的边缘，其它的也发生在玻璃表面打孔处。玻璃的起裂位置仅仅是研究玻璃破裂的一方面，玻璃破裂时的温差，有荷载情况下玻璃表面温度的变化，玻璃首次破裂时间等都是研究玻璃破裂非常重要的参数。

表2 实验结果汇总表

2.1 玻璃表面温度变化

图5是不同风速下玻璃表面及热荷载侧近玻璃表面附近空气温度的变化曲线。可以看出，所有测点温度都在一直上升，且热荷载侧近玻璃表面附近空气的温度(TC11)从加热开始就大于玻璃表面任何一个测点的温度，一直持续到玻璃破裂。组合箱体内温度要高于玻璃表面所有测点的温度，因此箱体内空气与玻璃表面存在着热对流作用。玻璃不仅受到来自热辐射源的辐射加热作用，同时也受到玻璃热辐射源一侧空气的对流作用。热荷载侧近玻璃表面附近空气的温度变化存在两个不同的阶段。图5a中TC11的斜率变化说明空气的温度经历一个非常快的上升过程，之后温度的上升率慢慢变小，最后维持在一个相对稳定的状态，直至实验结束。观察玻璃两个表面温度的变化曲线发现：在玻璃的热荷载侧表面，TC1，TC3的温度要大于玻璃表面中心点的温度(TC9)，而TC9的温度又大于TC5和TC7的温度，即距水平面的高度越高，玻璃表面的温度越高，其原因是由于组合箱体内的空气受到热的作用温度上升，而热烟气在浮力的作用下向上流动，造成在箱体内上部的空气温度要高于下部空气的温度[11]，上部热空气对玻璃的加热作用要大于下部空气对玻璃的加热作用，从而使得在热荷载侧玻璃表面上部温度要高于下部温度。在观察风荷载侧玻璃表面的温度变化曲线呈现相同的变化规律，原因则可能是热荷载侧温度高的玻璃上部对风荷载一侧表面的传热作用更大。实验中出现的上部温度远高于下部中心点温度[12]，这与开放空间下测到的温度变化趋势不同。

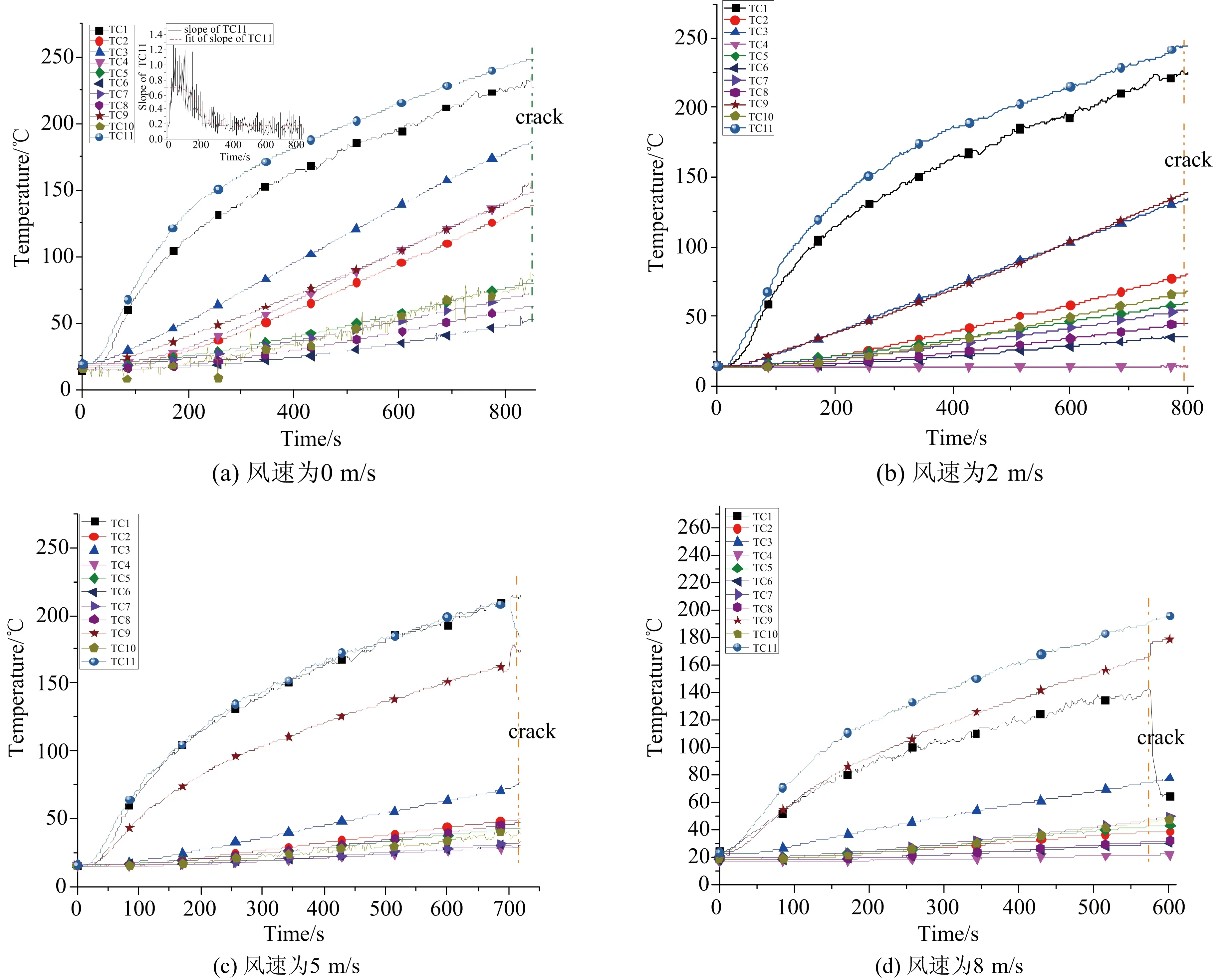
图5 不同风速下玻璃表面及附近空气温度随时间的变化曲线Fig.5 The variation of the temperature on the glass surface and inside cabinet in different conditions

图5a，图5b，图5c，图5d分别给出了四种工况下玻璃表面及附近空气温度随时间的变化曲线。实验结果表明，四种工况下，玻璃热荷载侧近玻璃表面空气的温度变化率基本相同。TC1，TC3，TC9在几组实验中都是玻璃表面温度最高的3个点，主要是因为热浮力的作用使得玻璃上部表面的温度要高于下部表面的温度。

图6是不同工况下风荷载一侧玻璃表面中心点温度。本文从每一种工况中选取一组实验中风荷载一侧玻璃表面中心点温度数据进行分析。所取数据从实验加热开始，到玻璃初次破裂结束(表2可知风速越大，玻璃发生初次破裂的时间越短)。可以看出，随着风荷载侧施加风速的增加，风荷载侧玻璃表面中心点温度呈递减的趋势。即在玻璃受热过程中，风荷载的引入有对玻璃风荷载侧表面降温的作用，且这种降温效果随风速增大而增强。

图6 不同工况下风荷载一侧玻璃表面中心点温度Fig.6 The variation of T10 in different conditions

图7 玻璃表面温差随时间的变化曲线(风速0m/s)Fig.7 The variation of temperature difference(ΔT1,ΔT2,ΔT) under no wind

图7是无风荷载状态下玻璃表面温差随时间的变化曲线。其中ΔT1是热荷载一侧玻璃表面和风荷载一侧玻璃表面的平均温度差，ΔT2是玻璃表面的最大温度差，ΔT是玻璃中心点热荷载一侧表面和风荷载一侧表面的温度差。由图7可知，玻璃表面的温差都是随时间而增大，其中ΔT2变化最大，而ΔT变化最缓慢。由于ΔT1考虑了玻璃表面所有的测点，得到的结果越趋向于真实值，因此，在此采用ΔT1进行分析。图7也可以看出使用这种定义方法更接近三者的平均值。

2.2 风速与玻璃破裂时间及温差的关系

实验结果显示12组实验中浮法玻璃全部破裂，本文统计了各实验工况初次发生破裂所需要的时间。结果表明：在无风荷载状态下，点式支承安装方式下玻璃发生初次破裂的平均时间是829 s，是这四种工况中发生首次破裂所需时间最长的；而在风荷载速度是8 m/s时，玻璃发生首次破裂的平均时间仅需要579 s，远小于无风状态下玻璃发生初次玻璃所需要的时间，即：玻璃风荷载侧表面受到的风荷载越大，其发生首次破裂所需要的时间越短。图8是玻璃首次破裂时间随风荷载变化的拟合曲线。比较无风荷载状态与有风荷载状态下的实验结果发现：保持玻璃受到的热辐射条件不变，玻璃两侧受到热荷载和风荷载双重作用时，风荷载的施加会加速玻璃的破裂，且玻璃受到的风荷载越大，这种加速作用就会越大。原因可能是玻璃在受热过程中由于热胀冷缩会导致产生向热辐射一侧的挠度，而风的作用会扩大这种挠度[13]，对玻璃的破裂起到加速作用。

图8 首次破裂时间随风速变化曲线Fig.8 Time to first break versus wind speed

图9是不同工况下温差ΔT1随时间的变化曲线。可以推断出：在玻璃两侧受到热荷载和风荷载双重作用时，玻璃表面的温差是随着时间递增的，玻璃内外表面的平均温差是不断扩大的。在无风状态下，玻璃首次起裂时温差为78℃，风荷载速度为2 m/s时，玻璃首次起裂时温差为75℃，风荷载速度为5 m/s时，玻璃首次起裂时温差为69℃，风荷载速度为8 m/s时，玻璃首次起裂时温差为62℃。即随着外部风荷载的增加，不仅首次起裂时间呈现递减趋势，同时首次破裂表面的温差ΔT1也呈现递减趋势。

图9 不同工况下温差ΔT1随时间变化曲线Fig.9 The variation of temperature difference ΔT1 in different conditions

玻璃的破裂是有热辐射产生的热应力和风荷载产生的机械应力共同作用的结果。根据公式1可知，玻璃内部的热应力与玻璃内部的温差是成正比。温差越大，则玻璃内部的热应力越大。而风压是与风速成正比的，风速越大，作用在玻璃表面的风压就越大。当作用在玻璃表面的风压越大，玻璃破裂时玻璃内部的热应力越小，不难推测出这两种作用是具有叠加效应的。因此，当玻璃两侧受到热辐射和风荷载双重作用时，风荷载产生的压力越大，玻璃破裂时玻璃内部的热应力越小(即玻璃内部温差越小)，而由于玻璃表面的温差随着时间的增加而增加，因此玻璃破裂所需的时间就越短。

2.3 裂纹的产生及扩展

在无风状态下玻璃起裂的位置全部经过四个支撑孔，但是在有风的情况下出现了3组经过从边缘破裂的情况(实验4、实验5和实验11)。所有的实验都是在同一种受热条件下：即热辐射功率为90 kW。可能原因是风荷载的施加改变了玻璃内部的应力分布，使得玻璃破裂时最大应力出现在玻璃的边缘，因而起裂的位置也发生在边缘。

图10 玻璃起裂时刻表面的裂纹扩展图(无风)Fig.10 Crack propagation figure when glass is broken under no wind

图11 玻璃起裂时刻表面的裂纹扩展图Fig.11 Crack propagation figure when glass is broken in difference conditions

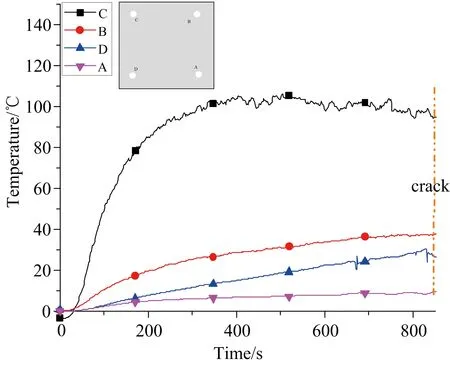
图12 实验2中四个支撑点的内外表面温差Fig.12 Temperature difference in the four support-points in Test 2

图10是无风状态下玻璃裂纹扩展图。相比于图10(a)和图10(b)，图10(c)在玻璃的下部形成孤岛1，但未脱落，2和3发生脱落。原因可能是因为为了保证实验腔体密封性的安装方式使得1部分在孤岛形成后脱落过程中受到玻璃框架的支撑作用没有完全的脱落，而2和3并没有受到这种支撑，所以发生了脱落。图12是实验2中四个支撑点(A，B，C，D)的内外表面温差。不难发现C点的温差最大，而A点的温差最小，而本组试验中起裂点发生在C处。所以在无风状态下，首次起裂位置主要发生在温差最大的支撑点处。

由图11可知，当玻璃首次起裂时，分布在玻璃表面的裂纹是随着施加在玻璃上风荷载的增加而变复杂的。由图10可知：在无风状态下分布在玻璃表面的裂纹很少，实验2为1个，实验1有两个，这两组工况也没有形成孤岛，而实验3裂纹为5条。图11(a)显示的风速为2 m/s时裂纹的个数是6条，图11(b)显示风速为5 m/s时裂纹的个数是8条，图11(c)显示风速为8 m/s时裂纹的个数是13条。即风荷载越大，在玻璃表面形成的裂纹越复杂。可能是因为风荷载改变了玻璃内部的应力分布，使玻璃的应力分布更复杂。一旦玻璃通过产生裂纹释放能量，会产生复杂的裂纹。

3 结论

本文研究外界风对点式支承浮法玻璃破裂行为的影响。重点研究了玻璃破裂时玻璃表面的温差和最大温差、首次破裂时间及玻璃起裂情况等。得出以下主要结论：

1.箱体内空气的温度在上升过程中温升速率不断下降。风荷载对玻璃表面具有冷却作用，降低了风荷载一侧玻璃表面中心点温度。

2.当玻璃两侧受到热荷载和风荷载双重作用时，玻璃发生破裂是由玻璃所受到的热应力与其受到的机械应力共同作用的结果，且这两种作用是有叠加效果的。玻璃破裂时所受到的机械应力越大，其破裂时玻璃内部所受到的热应力越小，反之亦然。

3.当玻璃两侧受到热荷载和风荷载双重作用时，玻璃风荷载一侧的风速越大，玻璃破裂所需时间越短。

4.在无风荷载作用下，玻璃破裂的起裂点往往发生在用于支撑玻璃的孔径处，但风荷载的作用会导致起裂点可能发生在玻璃的边缘。由于风荷载改变了玻璃内部的应力分布，因此风荷载越大，在玻璃表面形成的裂纹越复杂。

[1] 王志春，等. 风速对高度变化的曲线拟合[J]. 广东气象, 2008， 29(1): 13-15.

[2] 伍颖. 断裂与疲劳[M]. 武汉：中国地质大学出版社,2008,40-43.

[3] Emmons HW. The Need Fire Science[A]. Fire Safety Science - Proceedings of the 1st International Symposium[C], International Association for Fire Safety Science， 1986.

[4] Keski-Rahkonen O. Breaking of window glass close to fire[J]. Fire and Materials, 1988， 12(2): 61-69.

[5] Skelly MJ, et al. An Experimental investigation of glass breakage in compartment fire[J]. Journal of Fire Protection Engineering, 1991， 3(1): 25-34.

[6] Joshi AA, Pagni PJ. Fire-induced thermal fields in window glass. II-experiments[J]. Fire Safety Journal, 1994, 22(1): 45-65.

[7] Wang QS, et al. A stochastic analysis of glass crack initiation under thermal loading[J]. Application Thermal Engineering, 2014， 67(1-2): 447-457.

[8] Wang Y, et al. Effects of xing point positions on thermal response of four point-supported glass façades[J]. Construction and Building Materials, 2014， 73: 235-246.

[9] Brown WG. A practicable formulation for the strength of glass and its special application to large plates[M]. National Research Council Canada, 1974, 11.

[10] Gavanski E, Kopp GA. Storm and gust duration effects on design wind loads for glass[J]. Journal of Structural Engineering, 2011, 137(12): 1603-1610.

[11] 刘震. 小尺寸房间及走廊内烟气流动规律模拟研究[J]. http://www.paper.edu.cn, 2010.

[12] 邵光正. 火灾场景中水幕对玻璃破裂行为影响的实验研究[D]. 合肥：中国科学技术大学, 2015.

[13] 蒋凤昌. 点支式玻璃幕墙的结构计算与优化研究[D]. 镇江: 江苏大学, 2003.

Breakage of float glass with four-point supported under the combined effect of thermal loading and wind loading

ZHAO Han, WANG Yu, WANG Qingsong, CHEN Haodong, SUN Jinhua

(State Key Laboratory of Fire Science, China University of Science and Technology , HeFei 230026, China)

The glass breakagebehavior is significantly affected by the compartment fire and environmental wind in high-rise building fire. In this work, the four-point supported glass panes, with a dimension of 600 mm× 600 mm× 6 mm, are employed in experiments to study the glass breakage behavior. The glass breaking time, crack initiation and propagation are obtained, and the temperature difference on the glass is calculated. The wind load significantly affects the response characteristics of glass breakage: When glass façade is under the combined effect of wind loading and thermal loading, the wind load can accelerate the glass fracture. The results provide useful knowledge for the fire protection of glass façades.

Glass façades; Thermal radiation; Wind load; Time to first crack

2016-03-12；修改日期：2016-04-25

国家自然科学基金(51578524)；国家重点研究基础发展计划(973计划)(2012CB719702)。

赵寒(1991-)，男，中国科学技术大学火灾科学国家重点实验室硕士研究生，研究方向为环境风与火灾耦合作用下玻璃的破裂机理研究。

王青松，E-mail：pinew@ustc.edu.cn

1004-5309(2016)-00093-07

10.3969/j.issn.1004-5309.2016.02.06

X93; X932

A