八数码问题解法效率比较及改进研究 

付宏杰王雪莹周健周孙静朱珠张俊余

摘要：八数码问题是人工智能中的一个典型问题，目前解决八数码问题的搜索求解策略主要有深度优先搜索、宽度优先搜索、启发式A*算法。对这些算法进行研究，重点对A*算法进行适当改进，使用曼哈顿距离对估价函数进行优化。对使用这些算法解决八数码问题的效率进行比较，从步数、时间、结点数、外显率等各参数，通过具体的实验数据分析，进一步验证各算法的特性。

关键词：八数码；深度优先搜索；宽度优先搜索；A*算法；曼哈顿距离

DOIDOI：10.11907/rjdk.161867

中图分类号：TP312

文献标识码：A文章编号文章编号：16727800（2016）009004105

基金项目基金项目：

作者简介作者简介：付宏杰（1973-），女，吉林公主岭人，博士，吉林工程技术师范学院信息工程学院副教授，研究方向为人工智能、群体智能、机器学习。

1问题描述

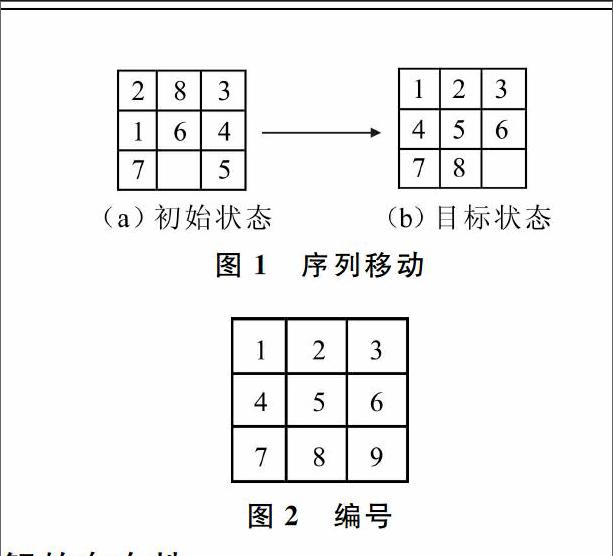
八数码问题就是在一个大小为3×3的九宫格上，放置8块编号为1～8的木块，九宫格中有一个空格，周围（上下左右）的木块可以和空格交换位置。对于问题，给定一个初始状态（如图1（a）初始状态），目标状态（如图1（b）目标状态）是期望达到1～8顺序排列的序列，并且空格在右下角，问题的实质就是寻找一个合法的移动序列。

2问题分析和模型表示

2.1模型建立

对于棋格，每个位置给定一个编号，从左上角开始顺序编号（见图2），对于任意的状态，记为p = s[0]s[1]s[2]s[3]s[4]s[5]s[6]s[7]s[8]，图1初始状态中的状态可以表示为 p=2 8 3 1 6 4 7 0 5，图2目标状态中的状态可以表示为 p = 1 2 3 4 5 6 7 8 0。

2.2分析解的存在性

不是每一个给定的初始状态都存在解，在分析之前，引入线性代数逆序和逆序数的概念：在一个排列中，如果一对数的前后位置和大小顺序相反，即前面的数大于后面的数，那么它们就成为一个逆序；排列中逆序的总数就成为这个排列的逆序数。例如，排列p=2 8 3 1 6 4 7 0 5的逆序数为1+6+1+0+2+0+1=11（不可解）。

使用线性代数理论可以论证，对于任意目标状态，只有初始状态的逆序数和目标状态的逆序数的奇偶性相同才有解（逆序数计算不包括0的逆序数）。例如p=1 2 3 4 5 6 7 0 8的逆序数为0，与p的逆序数奇偶性相同，因此是可解状态。

3搜索策略

搜索算法本质上是一棵将初始节点作为根节点的四叉树。从初始节点开始，以空白格向4个方向的移动作为分支。求解的过程就是寻找一条从根节点到目标结点的路径的过程。

为了方便论述，取目标状态为：p=1、2、3、4、5、6、7、8、0，本文用上、右、下、左分别表示空格的向上、向右、向下、向左4种操作。

3.1深度优先搜索算法（Depth-First-Search）

深度优先搜索策略是扩展当前结点，生成的子节点总是置于扩展栈的前端，这样搜索向纵深方向发展。

3.1.1算法策略

①将起始结点S加入栈中，如果此结点是目标结点，则得到解；②如果栈为空，则无解，失败退出，否则继续执行步骤Ⅲ；③将栈顶元素（记作结点N）从栈中取出；④如果结点N的深度等于最大深度，则转向步骤Ⅱ；⑤扩展结点N的所有结点，产生其全部的后继结点，并压入栈；⑥如果后继结点中有任一结点为目标结点，则求得解，否则转向步骤Ⅱ。

3.1.2搜索图解

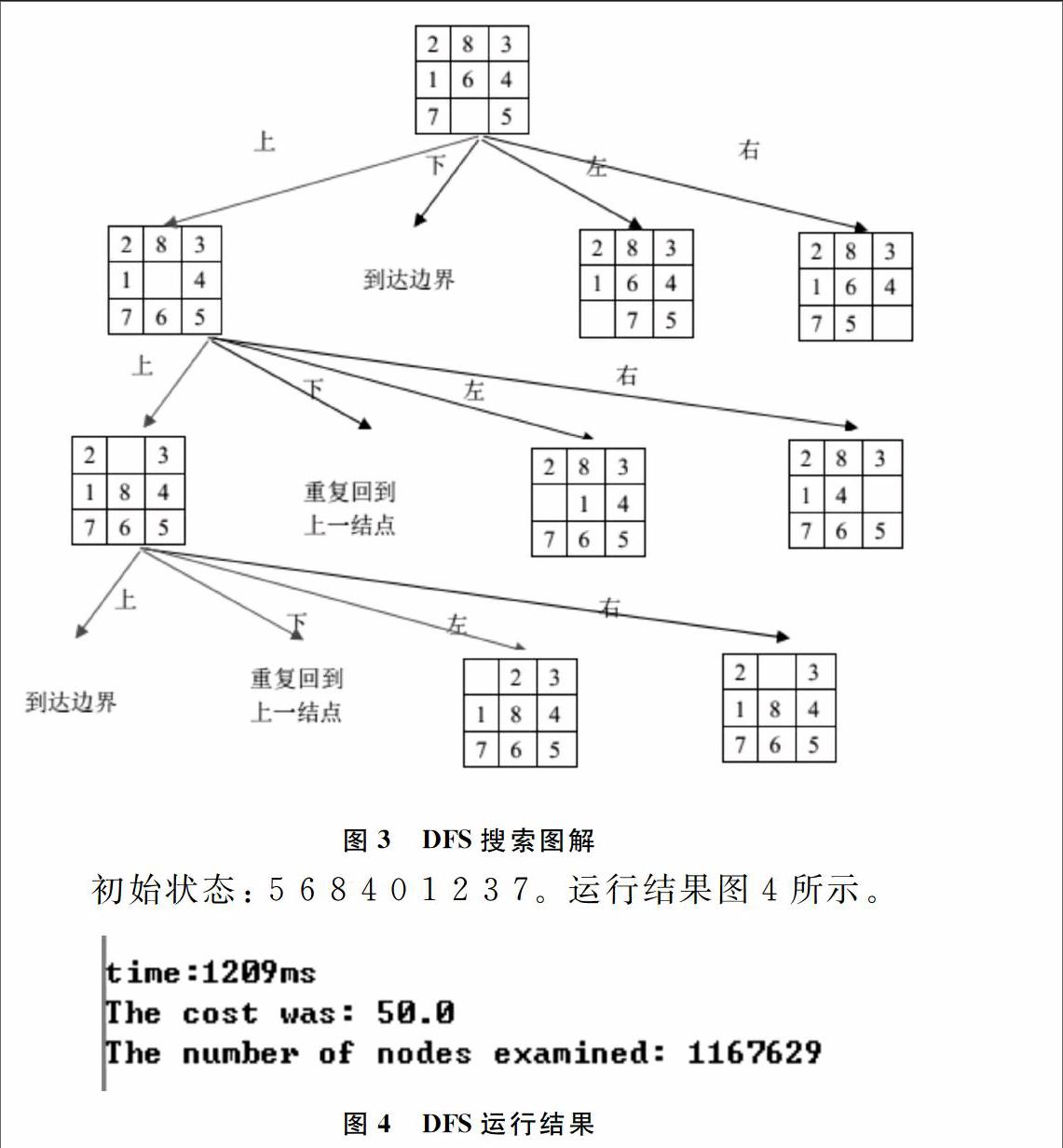
搜索图解如图3所示。

3.1.3算法优缺点分析

深度优先算法在解决八数码问题时有一个致命缺点，就是必须设置一个深度界限，否则，搜索会一直沿着纵深方向发展，会一直无法搜索到解路径。

即使加了限制条件，搜索到了解路径，解路径也不一定是最优解路径。

缺点：如果目标节点不在搜索进入的分支上，而该分支又是一个无穷分支，就得不到解，因此该算法是不完备的。

优点：如果目标节点在搜索进入的分支上，则可以较快得到解。

3.2宽度优先搜索算法（Breadth-First-Search）

宽度优先算法将扩展结点置于扩展队列的末端，使得搜索向横向发展。

3.2.1算法策略

①将起始结点放入队列中，如果该起始结点为一目标结点，则得到解；②如果队列为空，则无解，失败退出，否则继续步骤Ⅲ；③将第一个结点（记作结点N）放入队列中，并将它放入已扩展结点的队列中；④扩展结点N，如果没有后继结点，则转向步骤Ⅱ；⑤将N的所有后继结点放到队列末端，并提供从这些后继结点回到结点N的指针；⑥如果N的任一后继结点是个目标结点，则找到一个解（反向追踪得到从目标结点到起始结点的路径），成功退出，否则转向步骤Ⅱ。

宽度优先搜索对于八数码问题的解决情况，相较于深度优先搜索好，对于解决步数在20～30步的初始状态，可以在300～500ms内解决。

3.2.2搜索图解

搜索图解如图5所示。

3.2.3算法优缺点分析

宽度优先搜索，在搜索过程中，遵循一层一层往下搜索的搜索策略，它是一个完备的算法，找到的解一定是最优解。

缺点：当目标节点距离初始节点较远时会产生许多无用的节点，搜索效率低，只能适用于到达目标结点步数较少的情况，如果步数超过15步，运行时间太长，则不再起作用。

优点：只要问题有解，则总可以得到解，而且是最短路径的解。

3.3A*算法

A*算法的基本思想与广度优先算法相同，但是在扩展出一个结点后，要计算它的估价函数，并根据估价函数对待扩展的结点排序，从而保证每次扩展的结点都是估价函数最小的结点。

3.3.1算法思想

A*算法是一种常用的启发式搜索算法。在A*算法中，一个结点位置的好坏用估价函数来对它进行评估：

f（n）=g（n）+h（n）

这里，f（n）是估价函数，g（n）是起点到终点的最短路径值（也称为最小耗费或最小代价），h（n）是n到目标的最短路经的启发值。由于这个f（n）其实是无法预先知道的，因而实际上使用的是如下估价函数：

f（n）=g（n）+h（n）

其中，g（n）是从初始结点到节点n的实际代价，h（n）是从结点n到目标结点的最佳路径的估计代价。在这里主要是h（n）体现了搜索的启发信息，因为g（n）是已知的。用f（n）作为f（n）的近似，也即用g（n）代替g（n），h（n）代替h（n）。这样必须满足两个条件：①g（n）≥g（n）（大多数情况下都是满足的，可以不用考虑），且f必须保持单调递增；②h必须小于等于实际的从当前节点到达目标节点的最小耗费h（n）≤h（n）。第二点特别重要，可以证明应用这样的估价函数可以找到最短路径。

估价函数中，主要是计算h，对于不同的问题，h有不同的含义。这里的h（n）代表的是当前结点状态与目标结点状态相比没有到位的棋子数，是最简单的估价函数。

3.3.2算法策略

①建立一个队列，计算初始结点的估价函数f，并将初始结点入队，设置队列头和尾指针；②取出队列头（队列头指针所指）的结点，如果该结点是目标结点，则输出路径，程序结束。否则对结点进行扩展；③检查扩展出的新结点是否与队列中的结点重复，若与不能再扩展的结点重复，则将它抛弃，若新结点与待扩展的结点重复，则比较两个结点的估价函数中g的大小，保留较小g值的结点。跳至Ⅴ；④如果扩展出的新结点与队列中的结点不重复，则按照其估价函数f的大小将它插入队列中的头结点之后待扩展结点的适当位置，使它们按从小到大的顺序排列，最后更新队列尾指针；⑤如果队列头的结点还可以扩展，直接返回步骤②，否则将队列头指针指向下一结点，再返回步骤②。

3.3.3搜索图解

搜索图解如图7所示。

3.3.4算法优缺点分析

优点：A*算法在绝大多数的情况下，在性能方面都远远优与DFS和BFS。算法的主要运行性能，取决于估价函数f的选取。

缺点：由于算法本身的特点，因此根据估价函数找到的解路径不一定是最优解路径。

初始状态： 5 6 8 4 0 1 2 3 7。运行结果图8所示。

4算法改进

4.1状态表示方法压缩

有许多表示方法，比如一个3*3的八数码盘可以压缩成一个int值表示，但不适用于格子大于9的问题（如十五谜问题）。如果对空间要求很高，则还可以再压缩。本文采用整数（int）表示的方法。

表示方法如下：由于int的大小是32位（范围是[-2147483648-2147483648]），取一个int的低9位。为了方便寻找空格的位置，int的个位用来放空格的位置（1-9）。而前8位，按照行从上到下，列从左到右的顺序依次记录对应位置上的数字。

4.2哈希函数去重

高效避免访问同一个状态，最直接的方法是记录每一个状态访问与否，然后在衍生状态时不衍生那些已经访问的状态。基本思想是，给每个状态标记一个flag，若该状态flag = true则不衍生，若为false则衍生并修改flag为true。

每一次移动产生新状态时，先判断它是否已在两个链表中，若存在，则不衍生；若不存在，将其放入活链表。对于被衍生的那个状态，放入死链表。

为了记录每一个状态是否被访问过，需要有足够的空间。八数码问题一共有9！，这个数字并不是很大，采用哈希函数的方法，使复杂度减为O（1）。

4.3估价函数改进

通过找出不在位置的棋格个数形成的简单估价函数，不足以描述该结点到目标节点的路径长度。因此本文采用一种更为科学合理的距离函数，来描述两个状态结点之间的差距。设距离函数为h2（n），其函数值为当前结点状态不在位置的棋格，到它目标结点需要移动的距离：

h2（n）=|x-x0|+|y-y0|

使用此函数，对于A*算法的估价函数进行改进，能够取得比较明显的改进效果。

5效率比较

5.1概念

首先给出几个用来进行效率比价的变量：①步数（L）：从初始节点到达目标的路径长度；②时间（T）：搜索程序运行的时间，单位毫秒（ms）；③结点数（N）：整个过程中生成的节点总数（不包括初始节点）；④外显率（P）：搜索工程中，从初始节点向目标节点进行搜索的区域的宽度。

P=LN；P∈（0，1]

5.2实验数据分析

数据说明：①环境为Windows系统，语言为Java，使用控制台命令输出算法时间；②目标状态 1 2 3 4 5 6 7 8 9 0；③由于运行时间受系统影响很大，具有一定的随机性，因而每个状态执行3次，取中位数作为最终结果时间；④“长度”为该初始状态对应的最短路径的长度。实验数据及结论如表1～表5、图9～图12所示。

（1）八数码问题解路径长度比较。

（2）八数码问题解决时间比较。

（4）八数码问题外显率比较。

5.3研究结论

通过研究，可得结论如下：①DFS的解路径长度趋于搜索深度界限（本文界限是30），搜索效率受深度影响很大，并且搜索结点冗余多、速度慢；②BFS找到的一定是最优解，但是在算法效率上，虽然比DFS好，却远远不如A*算法，同时BFS在搜索深度较深时，产生的冗余结点较多；③A*算法在效率上相对最优，时间和空间上都比DFS和BFS更优，但缺点是，找到的解不一定是最优解；④改进的A*算法在时间复杂度和效率上都更优，空间利用率（外显率）与A*算法差距不大。总体而言，改进的算法取得了较好效果。

参考文献参考文献：

[1]蔡自兴.徐光.人工智能及其应用[M].北京：清华大学出版社，1996.

[2]唐朝舜.董玉德.八数码的启发式搜索算法及实现[J].安徽职业技术学院学报，2004，3（3）：912.

[3]陶阳.VS2008环境下八数码问题的BFS算法设计与实现[J].电脑知识与技术，2009（26）：1417.

[4]张信一.黎燕.基于A*算法的八数码问题的程序求解[J].现代计算机，2003，5（14）：1418.

[5]贺计文，宋承祥，刘弘.基于遗传算法的八数码问题的设计及实现[J].计算机技术与发展，2010（3）：2023.

[6]姚全珠，赵双瑞.基于状态空间搜索的ETL过程优化[J].计算机工程与应用，2007（26）：4446.

责任编辑（责任编辑：孙娟）