基于图像轮廓的角点检测算法*

李云红　姚　韵　贾利娜

(西安工程大学电子信息学院　西安　710048)



基于图像轮廓的角点检测算法*

李云红姚韵贾利娜

(西安工程大学电子信息学院西安710048)

利用Gabor滤波器的生物视觉特性,设计了一个基于图像轮廓的角点检测器,提出利用轮廓像素的梯度方向变化信息作为角点测度。首先,用Canny边缘检测器对图像边缘进行提取;然后,利用多边形近似来改善边缘,在轮廓之间填补空隙得到封闭的轮廓;最后,将Gabor滤波器平滑后的轮廓像素的主方向角度差作为角点测度进行检测角点。实验选用15张测试图片分别在旋转和噪声下评估检测重复率和定位误差,通过与CSS、He&Yung、CPDA角点检测器进行对比实验,所提算法提高了平均角点重复率,使平均定位误差有所降低。

角点检测; 图像轮廓; Gabor滤波器; 检测算法

Class NumberTN302

1　引言

角点是表征图像结构的重要信息,在仿射变换下具有稳定不变性。在许多图像处理领域中,角点检测往往扮演着重要的角色,例如,图像配准、立体匹配、运动跟踪和目标识别[1～5]。已有的角点检测器,大致可分为三类：基于梯度的方法[6～9]、基于模板的方法[10～11]、基于轮廓的方法[12～14]。

基于梯度的检测器是通过检查图像局部灰度值的变化作为角点测度。Moravec发现了角点处的灰度变化在各个方向都很大,从而将该思想应用于基于梯度的检测[6]。从这个思想出发,Harris提出了著名的Harris检测器[7],将局部自相关矩阵的特征值作为角点测度,来反映角点与非角点的差异。基于模板的检测器是通过将图像的一小块区域与预先设定的模板匹配,Smith和Brady利用圆形模板提出了SUSAN检测算法[10],基本原理是中心像素与邻域内有相同亮度的像素点数目小于某个阈值,表明中心像素是角点,该方法可以有效抑制噪声,但定位精度较差,对复杂角点如“X”型交叉点的检测效果不好。文献[11]指出SUSAN检测器的圆形模板可以被一对带方向的交叉算子代替从而改善性能,基于模板的检测器有着低的运算复杂度但对噪声敏感,对含有复杂纹理的图像检测性能较差。基于轮廓的检测器是对图像进行边缘轮廓提取,角点测度定义在轮廓上,并区分于轮廓上的光滑像素点。Mokhtarian等提出了曲率尺度空间(Curvature-scale-space, CSS)的角点检测器[12],大尺度下的局部曲率被用于角点检测,小尺度下追踪角点并改善定位准确性,但CSS角点检测器有几个缺点：一是曲率计算利用二阶导数对轮廓的局部变化和噪声高度敏感;二是选择一个合适的高斯尺度平滑轮廓不容易的;三是角点阈值选取是一个问题;最后,因为轮廓上的相邻像素点只有八个方向,对于轮廓的变化方向,离散轮廓的局部曲率在图像栅格上的分辨率较低。Mohammad和Lu提出了利用弦到点的距离累加(chord-to-point distance accumulation, CPDA)技术[13],该算法部分克服了CSS算法的前两个缺陷。He和Yung[14]利用自适应曲率阈值部分克服了CSS算法的第三个缺陷从而改善CSS角点检测性能。

Gabor滤波器[15]拥有和脊椎动物视觉皮层感受野响应近似相似的性质,其常被运用在特征提取、指纹识别、人脸识别等领域。针对以上角点检测算法存在的问题,本文算法直接利用不同方向的 Gabor 滤波器对图像进行平滑,充分利用了提出利用边缘映射对应的像素点及领域内像素点的主方向角度差作为角点测度,以此来提高角点检测的准确性和噪声稳健性。通过与CSS[12]、He&Yung[14]、CPDA[13]角点检测器进行对比实验,结果表明论文提出的角点检测算法在旋转和噪声情况下有效地抑制了噪声对角点检测的影响,同时减少了角点漏检的概率。

2　基于图像轮廓的角点检测算法

2.1边缘轮廓线的提取

从图像的边缘映射提取完整的轮廓,定义为

C={P1,P2,…,PN}

(1)

其中PN=[xN,yN]T表示第N个轮廓上的像素,P1=PN表示轮廓线是环状的。

采用D-P[16]算法对于提取的轮廓线进行多边形近似来改善边缘。该算法将垂直距离作为化简指标,通过递推找出相对当前基线的最大偏移点,用这些偏移点来近似描述轮廓。

首先,连接曲线首末两点作为基线,计算出曲线上任意点到此基线的垂直距离,找出最大距离及最大距离对应的点并记录下来。

然后,如果最大距离小于预先设定的门限(通常取1.4),则只保留首末两点,其他的点全部舍弃;如果最大距离大于预先设定的门限,保留点并以该点为中心将曲线分成两部分,并分别对这两部分曲线重复前三步操作。

最后,当所有曲线都处理结束,依次连接保留的点,即可得到化简后的曲线。

利用D-P算法改善边缘轮廓线有很好的近似效果,提高了边缘轮廓线的定位精确度和噪声稳健性。

2.2角点测度的选择

在空间域中,一个二维Gabor滤波器是正弦高斯函数,形式为

x′=xcosθ+ysinθ

(2)

其中γ,η为沿x轴和y轴方向的锐度,f是滤波器的中心频率,θ是调制平面波和高斯主轴沿逆时针旋转的角度。在实际应用中,图像是离散的,对Gabor滤波器间隔采样得到像素各个方向上的灰度变化信息,离散的Gabor滤波器虚部幅值响应定义如下：

·sin(2πfsm′)

m′=mcosθk+nsinθ

n′=-msinθk+ncosθk

(3)

其中fs表示第s个尺度的中心频率,K表示方向采样个数,θk是第k个方向角度。图1显示八个方向的Gabor滤波器虚部频域图。

图1　8方向的Gabor 滤波器虚部频域图

每条轮廓上的像素点有8个领域,对应着8个方向。则采用8个方向的Gabor滤波器虚部与图像卷积得到图像8个方向的梯度幅值响应为

(4)

所以每个像素点对应的最大梯度方向及主方向角度定义为

(5)

由每个像素点对应的最大梯度方向值可以得出,沿轮廓线位于边缘像素点两侧最近的两个边缘像素点的主方向角度差。对于轮廓线上除端点以外的的角点测度为

(6)

对于轮廓线端点,若轮廓线为环形曲线(P1=PN时),其主方向角度差为

DA(1)=DA(N)≡

(7)

若轮廓线为开环曲线则主方向角度差为

(8)

将该主方向角度差作为提取候选角点的测度,与预先设定阈值的比较,大于阈值则判定为候选角点,否则,不予处理。

2.3角点判决

利用沿轮廓线的非极大值抑制处理进行角点判决,若像素点PN处的角点测度在给定邻域上是极大值同时大于已设定的阈值,满足：

DA(q)≥η,

DA(q)=max{DA(q+l),l=0,1,…,L}

(9)

则判定该边缘像素点为角点,η为判决阈值,2L+1是邻域大小,试验中取η=π/18,2L+1=5。从试验中发现,从一条轮廓线上检测的邻近角点距离很近,通过非极大值抑制处理去除掉这些邻近的角点,当5*5领域内包含多个角点时可将这些角点看作一个角点,位置是多个角点的几何中心。

根据上述内容,得出算法的基本步骤：

1) 利用Canny边缘轮廓检测器来提取图像边缘映射。

2) 利用多边形近似来改善边缘并填充边缘空隙得到封闭的轮廓。

3) 利用Gabor滤波器平滑轮廓,通过计算像素主方向与相邻像素方向角度之差DA。

4) 将方向角度的差值DA与预先设定的阈T进行比较,得出候选角点。

5) 在5*5领域内,对候选角点进行非极大值抑制,来提取角点。

3　实验结果与性能评估

为了验证所提算法的可行性,采用15幅图像如图2所示,分别用CSS[12],CPDA[13],He&Yung[14]及本文算法进行比较评估。首先对Gabor滤波器参数进行选择,经过实验比较平均检测率得出,Gabor滤波器参数为：γ=0.55,η=0.552,方向K取81。确定阈值T以及非极大值抑制窗口,试验中,阈值取为0.6,非极大值抑制窗口取为5×5。

图2　测试图像

对每幅图像在旋转变换和高斯噪声下得到仿射变换图像,利用平均重复率和定位误差来评价角点的检测性能,当检测到原图像与变换后的图像的角点距离小于等于4个像素时认为它们是重复的,反之不重复。对平均重复率定义为

(10)

其中Nt和No分别表示算法对旋转变换后图像和初始图像的检测角点数,Nr表示两者的重复角点数。定位误差定义为

(11)

图3给出了本文算法与其他三种算法的比较结果,变换图像在[-90°,90°]上每隔10°旋转一次,旋转18次;高斯噪声下,标准差在[1,15]区间,步长为1均匀取值。在高斯噪声和旋转角度不同情况下得到的角点数平均重复率和定位结果。

由图3、表1中可以得出,在不同角度的旋转变换下CSS和CPDA算法有较低的角点平均重复率,CSS的定位误差要小,由于基于灰度信息的角点检测算法对变换图像鲁棒性和稳定性好。相比较而言,He & Yung和所提算法比CSS和CPDA检测算法有较高的重复率,而本文提出的算法定位误差更小。

图3　实验比较图

算法旋转度数CSSCPDAHe&Yung本文算法检测结果RLεRLεRLεRLε-60°0.502.030.592.050.632.420.712.21-30°0.521.950.582.080.642.110.701.9030°0.511.940.602.100.652.270.712.2160°0.491.940.612.120.672.250.701.98

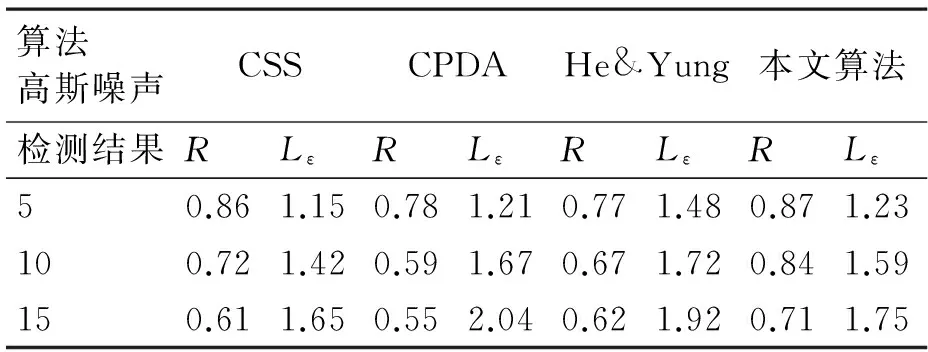
表2　不同高斯噪声下的角点平均重复率和定位误差

由图3、表2中可以得出,在高斯噪声下,CPDA和He&Yung算法有较低的角点平均重复率,CPDA的定位误差大。相比较而言,CSS和所提算法有小的定位误差,而本文算法角点的平均重复率高,故在高斯噪声下所提出的算法具有高的平均重复率和稳健性,综合上述得出新角点检测算法在噪声和旋转角度不同时,综合性能最佳。

4　结语

传统的基于轮廓线的角点检测算法是基于轮廓线的几何特征信息,而本文算法利用Gabor滤波器获取多个方向丰富的灰度强度变化信息,同时利用边缘映射上像素及其周围像素的最大梯度方向对应的信息熵来提取角点,使得角点检测能力和角点定位的准确性都有所提高。

[1] M. Awrangjeb, G. Lu. An improved curvature scale-space corner detector and a robust corner matching approach for transformed image identification[J].IEEE Transactions on Image Processing,2008,17(12):2425-2441.

[2] K. Mikolajczyk, C. Schmid. Scale & affine invariant interest point detectors[J]. International journal of computer vision,2004,60(1):63-86.

[3] Mohammad Awrangjeb,Guojun Lu. Performance comparisons of contour-based corner detectors[J]. IEEE Transactions on Image Processing,2012,21(9):4167-4179.

[4] L. Bretzner, T. Lindeberg. Feature tracking with automatic selection of spatial scales[J]. Computer Vision and Image Understanding,1998,71(3):385-392.

[5] E. Rosten. High performance rigid body tracking[D]. London: University of Cambridge,2006.

[6] Shui Peng-Lang, Zhang Wei-Chuan. Corner detection and classification using anisotropic directional derivative representations[J]. IEEE Transactions on Image Processing,2013,22(8):3204-3218.

[7] Wan L, Yu Z, Yang Q. Corner Detection Algorithm with Improved Harris[M]. Heidelberg: Springer Berlin Heidelberg,2015,525:260-271.

[8] Liao B, Xu J, Sun H, et al. Robust Corner Detection Based on Bilateral Filter in Direct Curvature Scale Space[J].Lecture Notes in Computer Science,2015,9142:357-365.

[9] Jiang W, Lam K M, Shen T Z. Efficient edge detection using simplified Gabor wavelets[J]. IEEE Transactions on Systems Man,2009,39(4):1036-1047.

[10] Zhang S, Yang D, Huang S, et al. Corner detection using Chebyshev fitting-based continuous curvature estimation[J]. Electronics Letters,2015,51(24):1988-1990.

[11] Bae S C,Kweon I S,Yoo C D. COP: A new corner detector[J]. Pattern Recognition Letters,2002,23(11):1349-1360.

[12] 徐玲.基于图像轮廓的角点检测方法研究[D].重庆:重庆大学,2009.

XU Ling.Research of corner detection method based on image contour[D]. Chongqing: Chongqing University,2009.

[13] Awrangjeb M, Lu G. Robust image corner detection based on the chord-to-point distance accumulation technique[J].IEEE Transactions on Multimedia,2008,10(6):1059-1072.

[14] He X C, Yung N H C. Corner detector based on global and local curvature properties[J]. Optical Engineering,2008,47(5):057008-057008.

[15] 张祥德,黎明奇,王琪,等.基于多方向Gabor滤波器和Adaboost的虹膜识别方法[J].东北大学学报,2012(1):39-42.

ZHANG Xiangde,LI Mingqi,WANG Qi.Based on multi orientation Gabor filters and AdaBoost of iris recognition method[J]. Journal of Northeastern University,2012(1):39-42.

[16] Douglas D H, Peucker T K. Algorithms for the reduction of the number of points required to represent a digitized line or its caricature[J].Cartographica The International Journal for Geographic Information and Geovisualization,1973,10(2):112-122.

Corner Detection Algorithm Based on Image Contour

LI YunhongYAO YunJIA Lina

(School of Electronic Information, Xi’an Polytechnic University, Xi’an710048)

According to the biological visual characteristics of the Gabor filter, a corner detection based on image contour is designed，using gradient direction change information of contour pixels is proposed as the corner measure. First, the image edges are extracted by Canny edge detector. Then, polygonal approximation is used to improve the edge, to fill gaps between the contour. Finally,the main direction angle difference of the contour pixels which is smoothed by the Gabor filter as the corner measure to detect corners.Fifteen different test images are used to test repetition rate and location error under the rotation and noise, with CSS, He&Yung, CPDA corner detection compared, the average angular repetition rate is improved,and the average positioning error is reduced.

corner detection, image contour, Gabor filter, detection algorithm

2016年4月7日,

2016年5月20日

国家级大学生创新创业项目(编号:201410709024)资助。

李云红,女,博士,教授,研究方向:红外热像技术,数字图像处理,信号与信息处理。姚韵,女,硕士研究生,研究方向:图像处理，信号与信息处理。贾利娜,女,硕士研究生,研究方向:控制工程。

TN302

10.3969/j.issn.1672-9722.2016.10.032