基于光子晶体和法布里珀罗腔结构的折射率传感器
高 伦,梁斌明,王 婷,陈家璧
(上海理工大学 光电信息与计算机工程学院,上海 200092)
基于光子晶体和法布里珀罗腔结构的折射率传感器
高伦,梁斌明,王婷,陈家璧
(上海理工大学 光电信息与计算机工程学院,上海200092)
光子晶体传感器在溶液检测方面具有巨大的应用潜力,设计一种光子晶体液体折射率传感器,通过在光子晶体中构造法布里珀罗腔(F-P腔)并利用光子晶体的自准直效应来实现折射率的探测。通过二维时域有限差分法(2D-FDTD)对电磁波在光子晶体F-P腔中的传播的仿真实验,最终获得了高线性度的输出光功率与液体折射率的对应关系,并可基于此特性实现液体折射率的检测。相较于其他的检测方法,光子晶体的应用使其具有体积小、测量范围广、易于与激光器件集成并且不受外界电磁环境影响等优点。
光子晶体; F-P腔; 液体折射率; 自准直效应
引 言
光子晶体是一种介电常数周期性分布人工结构材料[1],其最显著的特点是具有光子带隙(PBG)。随着人们的深入挖掘,光子晶体又展现出自准直效应等诸多新特性[2]。自准直效应即光束可以在不引入传统光子晶体波导的情况下,克服衍射发散效应而显示出几乎完全准直的传播特性。通常在光子晶体的频图上的特定频率区间存在着非常平坦的等频率面。由于光能量的传播总是垂直于等频面,因而这一频率范围的光在光子晶体里只能沿着一个特定的方向传播,从而发生自准直效应。与传统缺陷型光子晶体波导相比,自准直模处于导带中,因而有更大的群速度,另外自准直效应的光学器件对工艺精度要求不高,因而更适于工艺实现。
液体折射率传感器是近年来研究的一个热点,其广泛应用于化学,生物制药,环境监测等领域中。最传统的方法就是利用光在液体中的传播规律来测定液体折射率,如最小偏向角法[3]和掠射法[4]等,但这些方法过于复杂,且机械测量易带来误差。随着进一步的探索,科研工作者们发现光纤折射率传感器[5-9]主要是通过测量谐振波长的移动变化来获得所对应的折射率变化。文献[5]设计了一种基于光子晶体光纤的M-Z干涉仪进行折射率的探测,Nguyen等[9]也报道了一种法布里珀罗型折射率传感器。这类传感器表现出较高的灵敏度,但是测量范围往往有限,如文献[5]和[8]中报道的传感器的液体折射率测量范围分别为1.333~1.356和1.333~1.422。
本文提出了一种基于光子晶体F-P腔结构的液体折射率传感器。利用光子晶体的自准直效应和F-P腔的特性,可得到随待测液体折射率变化的光功率曲线。该传感器结构简单,测量方便快捷,线性度高且对工作波长要求不严格,液体折射率的探测范围为1.3~1.5,具有广泛的应用前景。
1 原理
1.1液体折射率传感器结构
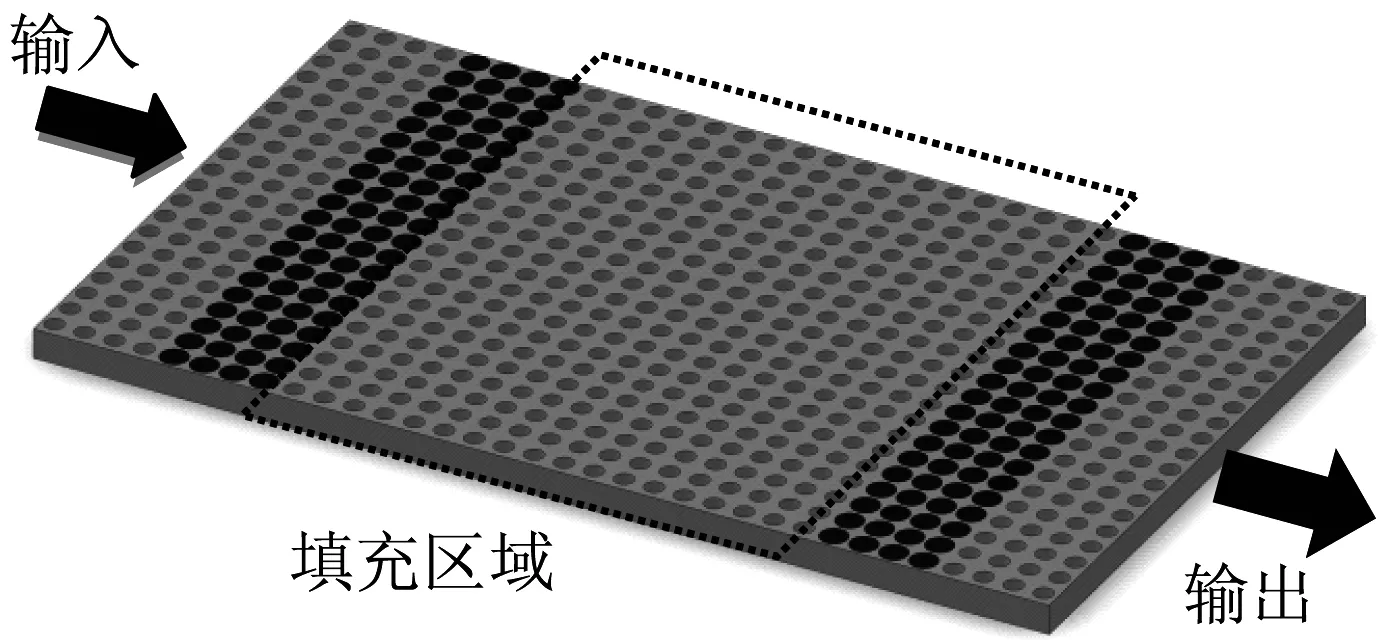
图1 二维空气孔型硅基光子晶体立体图
该传感器中所用的光子晶体是二维空气孔型正方格子硅基光子晶体,高纯硅的相对介电常数为11.56。光子晶体的晶格常数为a,空气孔直径D1=0.64a。其中有两组四排的空气孔作为F-P腔的反射结构。将待测液体填充于整个F-P腔两组反射结构中间的空气孔中。整个液体折射率传感器的结构如图1所示。
1.2工作原理
利用光子晶体自准直效应可使激光在光子晶体内沿固定方向传播。当二维空气孔型正方格子硅基光子晶体的空气孔直径为D1=0.64a时,分别计算了在液体折射率为1.3和1.5时(待测液体折射率的最大值和最小值),其TE模第一能带的等频图。从图2中可以看到频率在0.271 7~0.273 7(a/λ)的等频面在垂直Kx方向是很平坦的,因此,当电磁波在光子晶体中传输时在此频率附近会产生自准直效应[10]。

图2 填充待测液体的光子晶体等频图
当电磁波入射到F-P腔中时,会在反射结构间来回反射,出射光以多光束干涉的形式输出。根据多光束干涉原理,F-P腔中透射率函数由下式给出
(1)
式中:R为两反射结构的端面反射率;λ为光波波长;n为腔内介质的折射率;L为F-P腔的腔长;δ为两束相邻反射光的相位差。
(2)
由式(1)、(2)可知,在入射光波波长λ一定的情况下,当液体折射率改变时,F-P腔的光学腔长nL同时发生变化,相应地可以调制出射电磁波的能量。根据这一特性,则可以反向推测出待测液体的折射率,其在不同归一化频率下的光功率输出曲线如图3(a)所示。
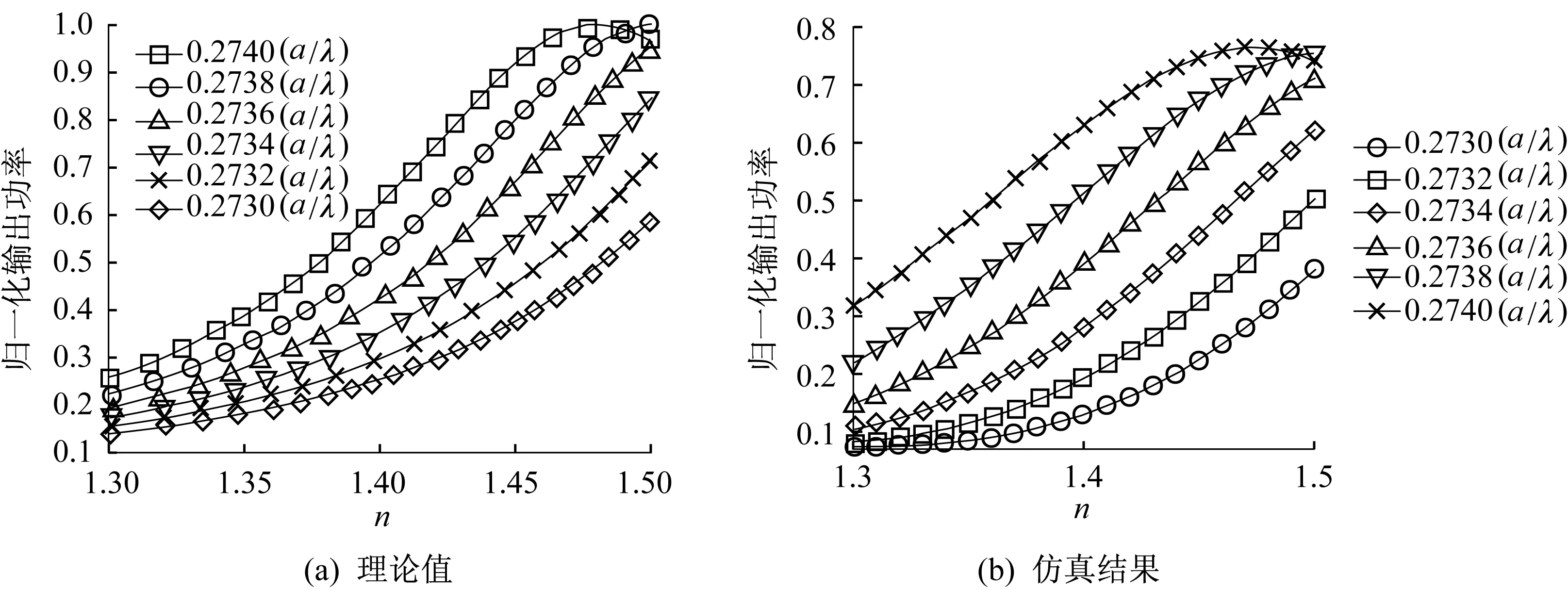
图3 不同归一化频率在液体折射率变化时的输出曲线
2 实验结果和分析
2.1仿真分析
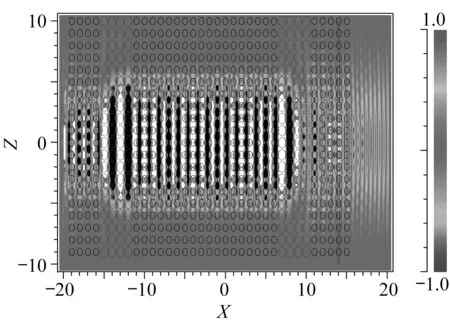
图4 光波在光子晶体F-P腔中的传播图
该折射率传感器的性能可用二维有限时域差分法(2D-FDTD)[11]进行分析。传感器由二维硅基空气孔型正方格子光子晶体构成,整个器件尺寸为34a×20a,其前后的四排介质柱用于自准直的输入和输出,输出端放置一光功率探测器。两组四排介质柱的反射结构之间为18a×20a的填充液体的区域,反射结构直径为D2=0.904a,液体折射率n的范围为1.3~1.5。输入端以宽度为8a的TE模式电磁波入射,整个边界采用完美匹配层。
在相应自准直频率区间,选择0.273~0.274(a/λ)的范围内以0.000 2为步长仿真传感器在液体折射率下的光功率输出曲线,结果如图4所示。
从图3中可以看出,仿真得出的曲线与理论推算的曲线基本一致。在0.273~0.274(a/λ)的归一化频率范围内,当待测液体折射率增加时,输出光功率也随之增大。为了得到最优的n-p曲线,在结构参数中,选择0.273 7的归一化频率作为折射率传感器的入射光频率。经过线性拟合,得到的结果如图5所示。
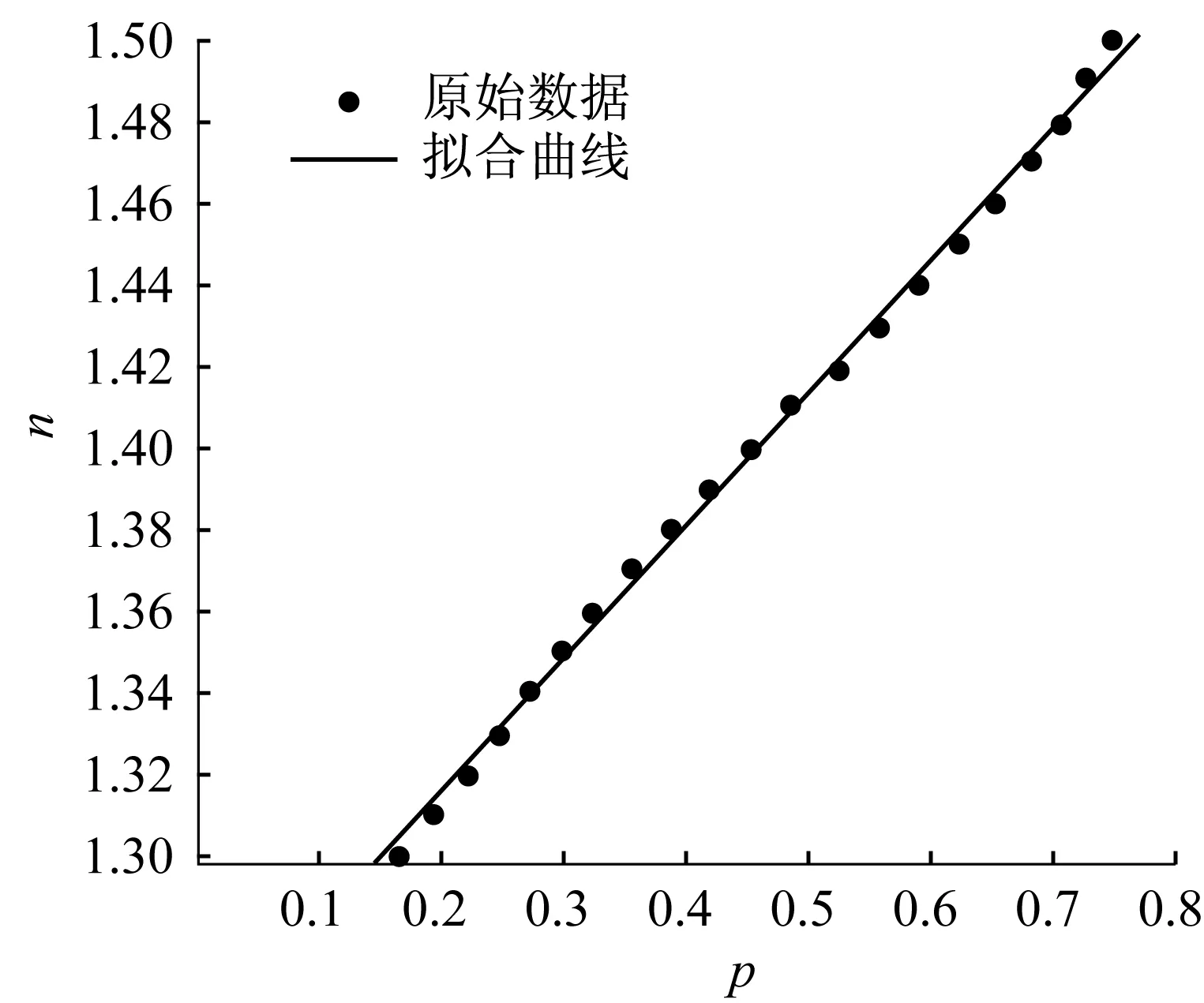
图5 待测液体折射率n与输出光功率p的拟合曲线
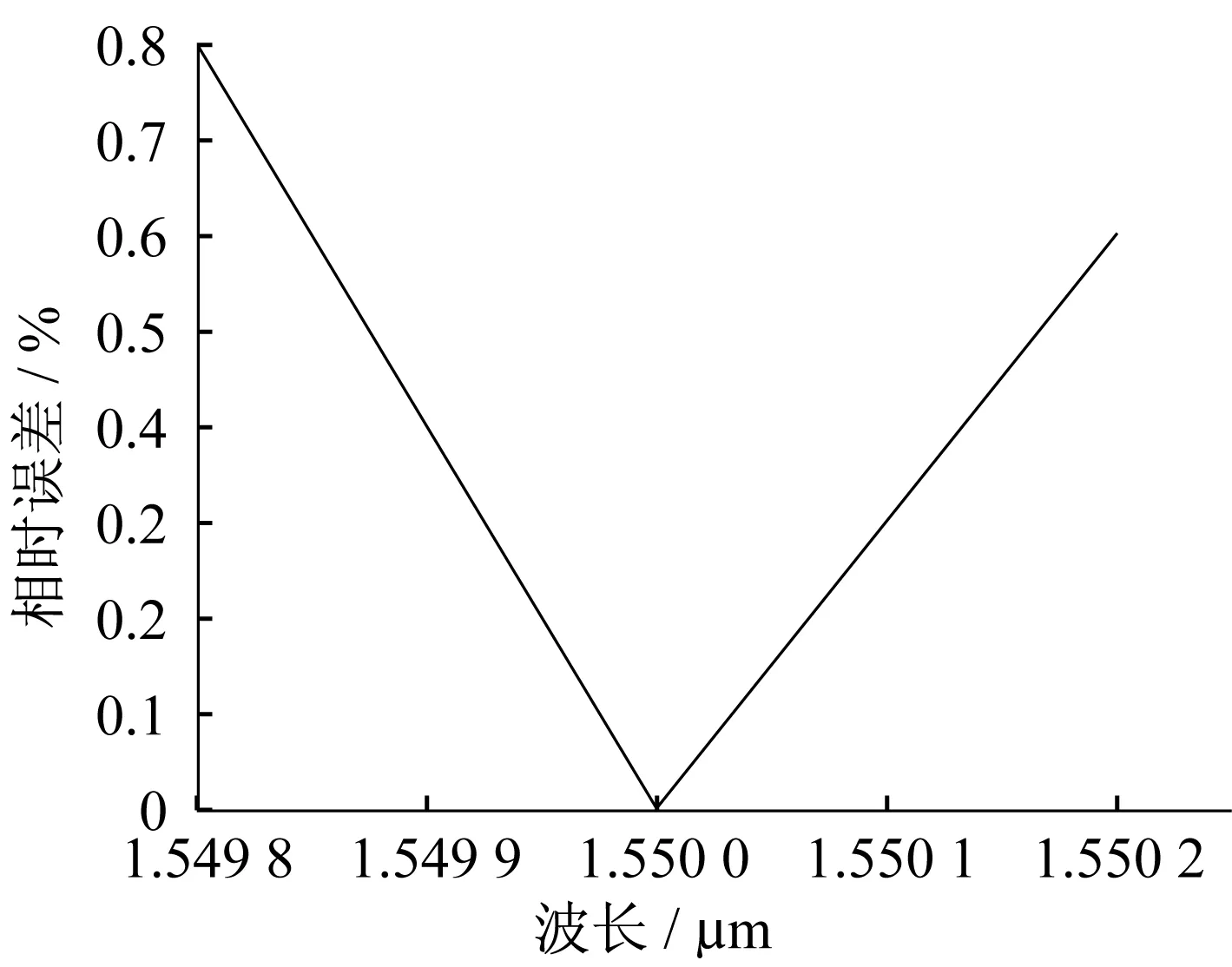
图6 激光光源带宽对传感器的误差分析
图5所示的关系曲线的线性拟合度为99.78%,拟合出n-p关系式:n=0.327 6p+1.25。由该n-p关系,可以应用于液体折射率传感器。在实际液体折射率传感器设计中,当激光器的输出波长λ=1.55 μm时,由归一化频率freq=0.273 7(a/λ)可计算出光子晶体的晶格常数a=λ×freq=0.424 2 μm。由探测到的输出光功率,根据n-p关系式,就能很快地得到待测液体的折射率。
4 误差分析
从图3可以看出不同的入射光频率会对输出功率产生一定影响。为确定激光器带宽对折射率传感器可能造成的影响,我们选择以折射率为1.38的酒精溶液进行分析。市面上激光器的光源带宽一般小于1 nm,可在此带宽范围内讨论折射率传感器的相对误差,其结果如图6所示。
从图6中可以看出,激光光源的波长漂移在1 nm的带宽范围(1.549 9~1.550 1 μm)内的折射率相对误差小于0.4%,说明该液体折射率传感器对光源的要求不高。
5 结 论
本文提出了一种新型的利用光子晶体探测液体折射率的装置,利用在光子晶体中构造的F-P腔的结构可实现电磁波在腔内的震荡,而待测液体折射率的变化可以改变相应的光学腔长,从而对输出光功率进行调制。同时,利用光子晶体的自准直效应,能极大的减小光泄露的情况,保证了该器件工作的稳定性。该液体折射率传感器具有结构简单、体积小且可在1.3~1.5的折射率范围内实现高线性度的测量,在生物化学领域具有潜在的应用前景。
[1]CULSHAW I S,ASTRATOV V N,STEVENSON R M,et al.Determination of the band structure of photonic crystal waveguides[J].Physica E:Low-dimensional Systems and Nanostructures,2000,7(3/4):650-655.
[2]KOSAKA H,KAWASHIMA T,TOMITA A,et al.Self-collimating phenomena in photonic crystals[J].Applied Physics Letters,1999,1999, 74(9): 1212-1214.
[3]温建平,唐运爱,钟远军,等.最小偏向角法测液体折射率实验的研究[J].实验室科学,2014,17(2):20-23.
[4]张庆,王小怀.掠射法测液体折射率时折射角与介质折射率的关系[J].韩山师范学院学报,2005,26(3):24-26.
[5]周赢武.基于光纤M-Z干涉的高灵敏度液体折射率传感器的实验研究[J].光子学报,2012,41(7):841-844.
[6]ZHANG S S,ZHANG W G,GENG P C,et al.Fiber Mach-Zehnder interferometer based on concatenated down- and up-tapers for refractive index sensing applications[J].Optics Communications,2013,288:47-51.
[7]李辉栋,傅海威,邵敏,等.基于光纤气泡和纤芯失配的Mach-Zehnder干涉液体折射率传感器[J].物理学报,2013,62(21):214209.
[8]WANG J N,TANG J L.Photonic crystal fiber Mach-Zehnder interferometer for refractive index sensing[J].Sensors,2012,12(3):2983-2995.
[9]NGUYEN L V,VASILIEV M,ALAMEH K.Three-wave fiber Fabry-Pérot interferometer for simultaneous measurement of temperature and water salinity of seawater[J].IEEE Photonics Technology Letters,2011,23(7):450-452.
[10]TURDUEV M,GIDEN I H,KURT H.Extraordinary wavelength dependence of self-collimation effect in photonic crystal with low structural symmetry[J].Photonics and Nanostructures-Fundamentals and Applications,2013,11(3):241-252.
[11]刘珂,杨冬晓.FDTD方法在光子晶体光纤中的应用[J].光学仪器,2005,27(4):22-25.
(编辑:张磊)
Refractive index sensor based on photonic crystal and Fabry-Perot cavity
GAO Lun,LIANG Binming,WANG Ting,CHEN Jiabi
(School of Optical-Electrical and Computer Engineering,University of Shanghai for Science and Technology,Shanghai 200092,China)
Photonic crystal sensor has great potential in solution detection.A refractive index sensor based on photonic crystal is presented.It was made by constructing a Fabry-Perot cavity(F-P cavity)in the photonic crystal where self-collimation effect was also applied.Through the simulation experiment of electromagnetic wave propagation in photonic crystal by two-dimensional finite difference time domain method (2D-FDTD),the high linearity corresponding relationship between the liquid refractive index and the output power was finally obtained.Thus the liquid refractive index sensor can be realized based on this relation.Compared with other detection methods,the application of photonic crystal has the advantage of smaller size,wider detection range,easier integration with other laser devices,independence from electromagnetic environment,etc.
photonic crystal; F-P cavity; liquid refractive index; self-collimation effect
2015-09-15
国家项目基础研究项目(2011CB707504);国家自然科学基金(61177043,11104184)
高伦(1991—),男,硕士研究生,主要从事光子晶体理论及器件方面的研究。E-mail:365661261@qq.com
梁斌明(1977—),男,副教授,主要从事新型微纳米材料和电磁理论等方面研究。E-mail:bmliang78@qq.com
1005-5630( 2016) 03-0248-04
TN252
A
10.3969/j.issn.1005-5630.2016.03.011

