高中数学对物理成绩影响的量化研究

赵阳

(华东师范大学课程与教学系， 上海 200062)



高中数学对物理成绩影响的量化研究

赵阳

(华东师范大学课程与教学系， 上海 200062)

数学与物理同为理科,它们之间有一定的相关性,高中数学对物理成绩的影响是客观存在的。本文在解读学科特点和高考考纲的基础上，以近5年江苏省高考物理试卷为样本一，靖江市某中学高二学生成绩为样本二，通过量化分析的方法探讨高中数学对物理成绩的影响和不同层次学生物理成绩受数学影响的程度。结果显示：高中数学知识点在物理学习中有很多运用，其中以解方程或不等式、解析几何、向量这三个数学知识点最多；高中数学成绩与物理成绩呈现出显著的正线性相关，且线性相关性高于语文、英语学科；高中物理学困生与数学成绩相关性最大，物理学优生与数学成绩相关性最小。

高中物理成绩数学方法相关分析量化研究

数学是学习其他理科科目的基础，而物理就是一门对数学知识要求较高的学科。学生从小学就开始学习数学，主要包括代数、几何、概率、推理与证明几个模块，而物理从初中开始学习，接触声学、光学、力学、电学，高中除了以上部分，还加入了电磁学等。高中物理的学习难度直线上升，初中数学基础薄弱的学生在高中物理学习上显得尤为吃力。解决物理问题需要良好的数学能力。本文通过分析近几年江苏物理高考题和学生成绩数据样本，以高中数学对物理成绩的影响展开量化研究。

一、研究背景

(一)物理学科的特点

1.物理学科包括物理知识、物理观念、科学方法和实验基础[1]。物理是一门严密的科学，定量精确度高，如分子物理学、纳米科技的运用。同时，它还是带有方法论的科学。物理知识都是以大量的实验为依托，运用科学的方法开展多次实验，才能验证得的到物理定律。学习物理，首先要有物理观念，从物理的思维角度去观察实验现象，观察生活中的物理情境。

2.实验、物理思想和数学是物理知识的三个基本要素[2]。任何一个物理知识，除了极少部分使用纯文字表述，其余都是以数学符号语言来表征。所以说，数学是物理的语言和工具。发现物理规律，不是简单的计算，是需要进行无数次前期实验和后期数据分析、归纳的。函数是数据分析的有力助手。例如，描述一个简单的物理事实——抛物线运动，包括实验测试手段、物理观点和数学公式、数据或曲线。所以，研究物理问题，实验、物理思想和数学是必不可少的。

3.物理学的核心在于建立物理模型。每一个物理问题，物理实验都可以转化为一个物理模型，每一个物理模型就是一个物理现象，生活中的情境可以提炼出一个理想化物理模型来加以研究。数学中同样也有建模的思想，这与物理学是一致的。物理模型在于多了物理知识。物理学的发展离不开一个个物理模型，例如焦耳的热能模型、行星的运动模型。

(二)从高考考纲看数学与物理的交叉性

1.理性思维与逻辑推理。物理是理性的学科，不像语文或历史学科开放性高。物理高考考纲中明确指出，要培养学生科学、理性的思维能力，发现自然科学问题，能够从科学现象中结合已有的知识或者题目中给出的事实、条件开展逻辑推理与论证。这与数学高考考纲中锻炼数学思维能力、通过图表信息解决数学问题、能够从特殊问题推理得到一般问题的数学规律是相一致的。学习理科，对问题的思考与解答要严谨、精密，同时透过现象展开合理的推理，提出新的问题，并且解决问题。

2.构建模型与数值运算。物理学的发展离不开物理模型，宏观的、微观的自然现象提炼出物理模型展开实验。同样，学生的物理学习也需要建立物理模型。题目中往往已经建立好模型，学生需要分析模型，进行数值计算。其中就包含了对一些数学模型的运用，例如三角函数、自由落体运动的二次函数。数学模型是解决物理模型的钥匙。有的物理问题要求学生自己设计实验、建立模型，通过对条件或者已有数据的分析，结合数学方法，成功借助数学模型来研究物理问题。如，物体的质量与体积就存在正比例的关系，同一压力、压强与受力面积存在反比例的关系。

3.平面作图与空间想象。物理高考考纲中要求学生学会对图形进行分解、组合，如力学中对力的分解与组合是解决力学问题的第一步。这就需要学生具有良好的数学平面作图能力与数值计算能力。同样，在电磁学中，学生要能够熟练分析电场和磁场产生的作用，需要一定的空间想象能力。数学中同样强调学生能画出图形，根据图形分析得到基本元素，进行合理想象，从而解决问题；物理老师往往能画出整洁的图形，这是有道理的。清晰明了的模型分析很重要，空间想象与平面作图是对物理条件的深度剖析与思考。

二、问题的提出

通过对已有研究的收集和分析发现，目前数学对物理的影响研究是从多角度开展的，有的从数学与物理学理论的角度展开，有的从物理学历史中展开，有的从一线教学的角度加以研究。从研究条件考虑，本文将量化分析高二物理试卷中数学思想的分布和数学对物理成绩的影响。

三、已有研究综述

通过在中国知网上文献检索“数学对物理的作用”，发现20世纪90年代之前对数学与物理学科交叉影响的文章较少，20世纪90年代特别是进入21世纪以来，随着各轮课改的进行，渐渐专门有学者和教育工作者开始研究数学对物理教学的影响。

20世纪80年代，阎金铎及其学生通过建立物理学习的回归模型提出大学物理学科教育与高中物理、其他学科间有一定的关系。20世纪90年代，梁树森在其著作《物理学习论》中得出结论：“高中数学知识水平对普通物理学习具有显著的影响。”[3]物理成绩与数学成绩的显著性和一致性极为明显，说明数学对物理各方面的学习都有作用。

从2000年开始，部分一线物理教师在丰富的教学经验上开始思考数学对物理教学的影响。王明高(2006)在《数学思维在物理教学中的应用》中，以具体案例为依据，阐述了数学函数与几何方法在具体物理问题中的巧妙运用[4]；朱坤燕(2015)在《浅析数学方法在物理教学中的应用体现》中，从教学理论出发，指出物理解题的数学方法就是建立数学模型，将研究对象之间的关系进行合理的表达[5]，之后深入分析物理过程，选择合适的数学方法，最后运用数学知识总结验证结果。

当然，也有学者与教育者进行大量调查实验收集样本，从具体数据出发，运用统计分析手段展开数学对物理作用的相关研究。陈雨田(2005)用教育测量的科学方法抽样随州市高中近4万人3年的统考成绩，得出数学学习与物理学习呈正相关[6]。同样，张金宝(2015)等人通过对济南市6所中学766名学生进行物理分类试题实验[7]，发现数学学优生与学困生对物理问题分类表征层次进行差异显著检验，表现为数学学优生更多地倾向物理问题的内在分类表征，学困生则倾向于对物理问题的外在分类表征，反映出数学影响学生对物理问题的分析。

通过上述已有研究发现，数学方法对物理学习尤为重要。在解决物理题目时应用较广泛，数学方法的种类也较多；数学成绩与物理成绩有相关性，并且呈正相关；各学科成绩对物理成绩相关性比较的研究、不同层次学生的数学学习对物理成绩的影响研究较少。

基于以上的研究综述，本文将从5份物理高考统考试卷中归纳出运用的数学方法与其比重，通过样本分析各学科对物理成绩的相关性影响以及物理学优生、中等生、学困生受数学成绩的影响力来说明数学对物理成绩的影响。

四、研究设计

(一)研究目的

本文以近5年江苏省物理高考试卷为样本一，以靖江市某重点高中高二理科班2015—2016学年度上学期750名学生的期末各科(语文、数学、英语、物理)成绩为样本二，旨在通过量化分析高中数学对物理成绩的影响。

(二)研究假设

根据国内外已有的研究综述，本文试图分析高中数学对物理成绩的影响。根据研究目的提出研究假设——靖江市高二学生数学学习对物理成绩有影响。

(三)样本选取及处理

样本一通过试卷及其专家的答案解析归纳出解题中所涉及的数学思想方法。

样本二的研究对象共有759人，去除缺考的9人，实际样本容量为750人。

(四)本研究的统计检验力

通过查阅相关文献，选取了6篇运用统计检验方法来研究数学对高中物理成绩影响的文章，发现本研究的实际效应尺度(Effect Size)较小，约为0.3。由于成绩是定距性变量，所以研究高中数学与物理成绩的关系，选取皮尔森(Pearson)的简单相关系数，而与其对应的检验统计是t检验，定义α显著性水平为0.01，利用GPower3.1.5得出本研究的统计检验力(Power)为0.98，如表1所示。

表1　本研究的统计检验力及其相关指标

五、研究结果与分析

(一)近5年江苏高考物理试卷包含的数学知识点统计

学生进入高中学习数学时，会感觉到知识点的难度与广度都明显加大，而物理新知识的引入以及综合题目难度也让学生感到吃力，甚至会觉得物理公式会用，但是运用数学思想方法继续解决问题无法实施。高中物理学习中究竟牵涉到了哪些数学知识点与思想方法，通过阅读物理《高考考试说明》知识点的内容与说明发现，物理学习中包括解方程或不等式、三角函数、二次函数、向量、解三角形、归纳推理、简单多面体、概率、解析几何等等。

列举样本一考试说明中出现次数较多的5个数学知识与方法：解方程或不等式、二次函数、向量、解三角形、解析几何在高考试卷解答中的应用次数，如表2所示。

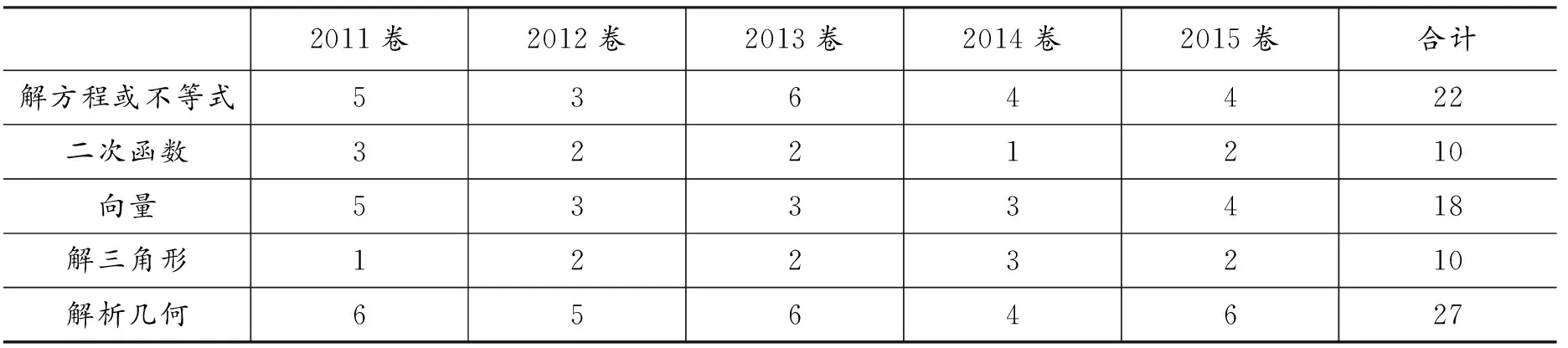
表2　近5年江苏省物理高考试卷应用数学知识次数的统计

分析表2发现，在近5年的江苏省物理高考中，运用解方程或不等式22次、二次函数10次、向量18次、解三角形10次、解析几何27次，按照由多到少的顺序排列，分别为：解方程或不等式、解析几何、向量、二次函数和解三角形。下面用饼状图来观察这5种数学方法在高考物理试卷中的出现比例，如图1所示。

从饼状图中可以看出，解方程或不等式比重最多，约占27.32%，因为数值计算是解决很多物理题目的必经过程；其次是解析几何，约占22.25%。从高考物理考纲中发现，电磁学等重要物理考点中都可能涉及到几何；第三是向量知识，约占18.21%。在力的分解与合成、速度等方面都有应用，且是物理考察的热点，这类题目难度系数都中等偏上；最后是解三角形和二次函数，比重较小，均约为10.11%。

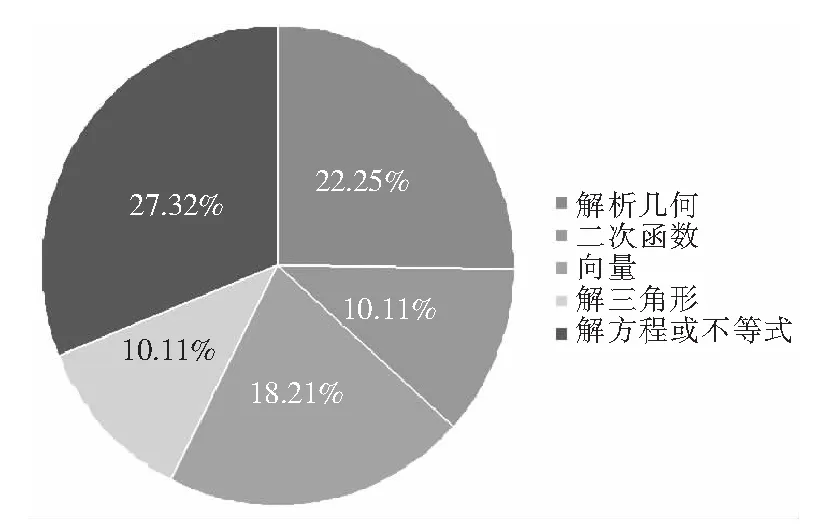
图1　5个数学知识点在高考物理中的应用比例

(二)高中各科目与物理成绩相关性的分析

以样本二为基础，分析语文、数学、英语与物理成绩之间的关系。函数关系能表达出变量之间一一对应的关系，但现实中语文、数学、英语和物理之间的关系并不是如此简单。研究各科成绩之间是否存在某种线性关系，我们可以利用SPSS 22.0软件进行相关分析。首先分别画出语文、数学、英语与物理成绩的简单散点图，结果如图2、图3、图4所示。

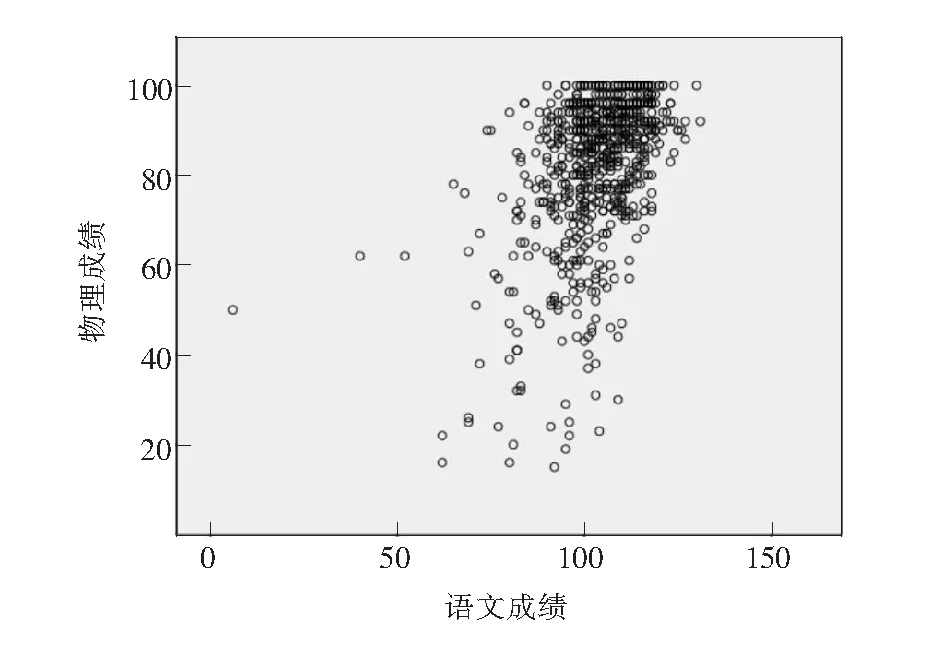
图2靖江市某校高二理科班750人期中考试(语文—物理)成绩

上面的简单散点图直观地提供了图中2个变量之间的相互关系，可以看出此次考试数学成绩与物理成绩呈正相关，语文、英语也大致与物理呈正相关，但是点的分布集中程度没有数学与物理关系图密集度高，线性关系明显。所以，我们可以得出语文、数学、英语与物理成绩呈正线性相关。相关性的强弱我们将进一步利用SPSS 22.0软件进行皮尔森(Pearson)简单相关系数分析。

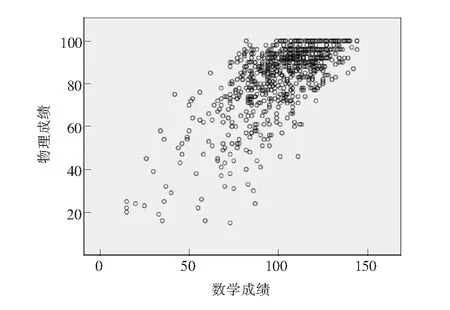
图3靖江市某校高二理科班750人期中考试(数学—物理)成绩

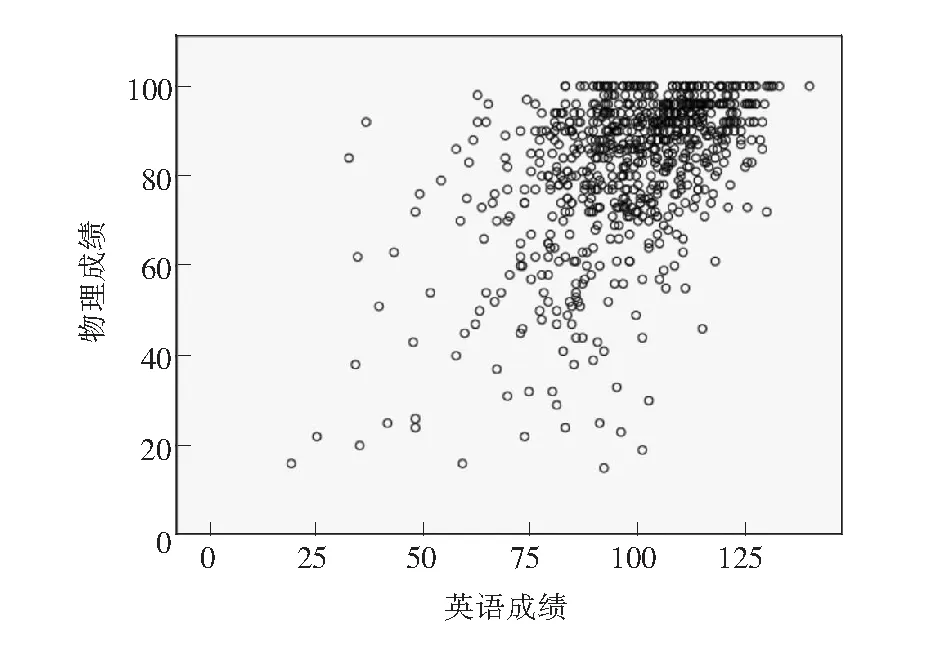
图4靖江市某校高二理科班750人期中考试(英语—物理)成绩

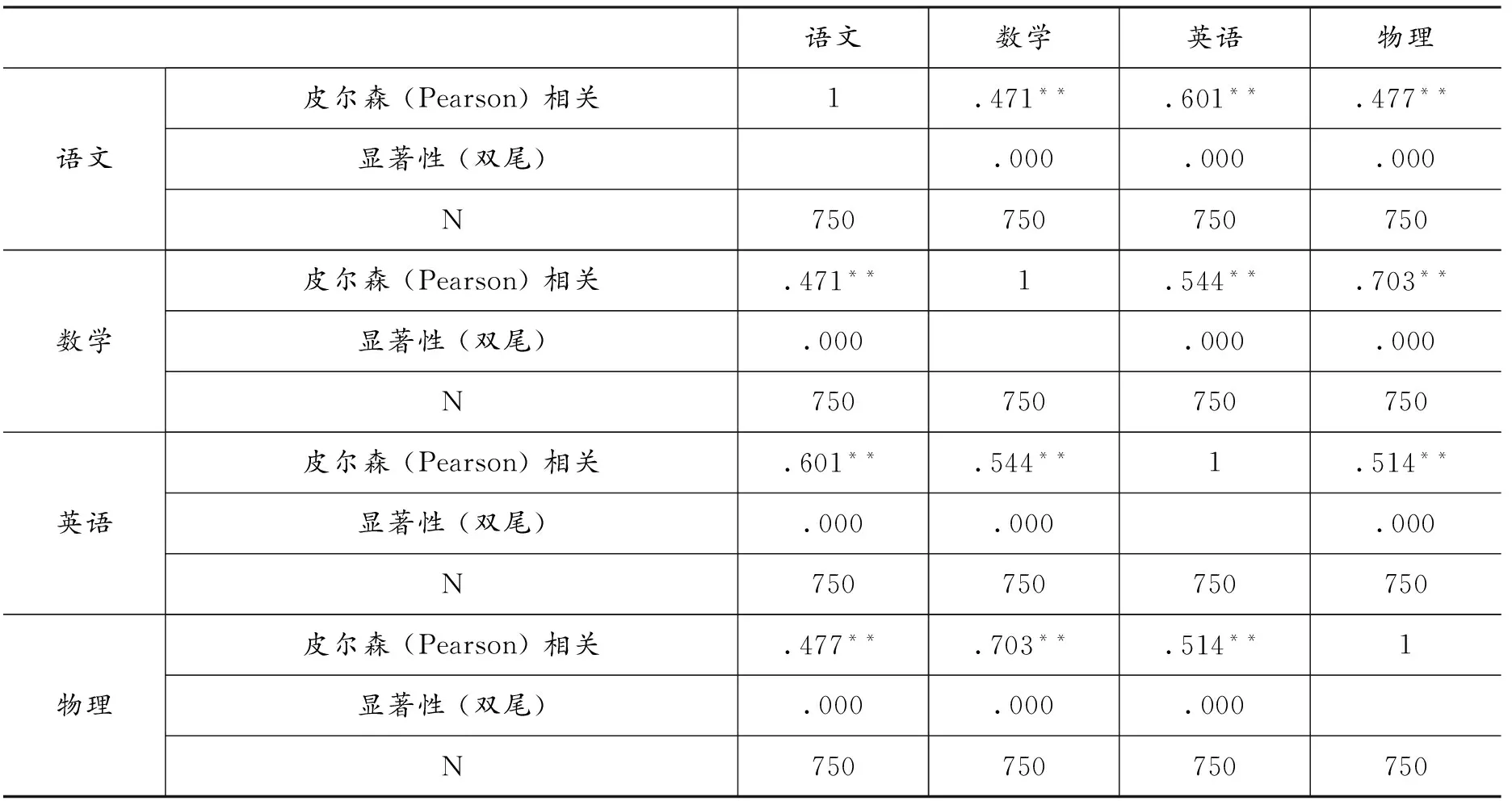
表3　物理和其他科目考试成绩的相关系数表

注：相关性在显著性水平α=0.01上，**表示P<0.01。

如表3所示，经过相关分析，实验结果如下：数学与物理的皮尔森(Pearson)简单相关系数r=0.703；英语与物理的皮尔森(Pearson)简单相关系数r=0.514；语文与物理的皮尔森 (Pearson)简单相关系数r=0.477。当0.3≤r<0.8时，2个变量总体呈现中度正线性相关。2个变量间的相关系数旁都是**，说明t检验结果相伴概率P<0.01，拒绝:2个变量之间不存在显著的线性相关，即语文、数学、英语与物理成绩之间存在显著的正线性关系。

通过比较得出，高中数学与物理呈现的相关性大于语文、英语和物理之间的相关性。所以说，高中数学对物理成绩有影响，数学基础好，有利于物理学习。

(三)高中不同层次学生数学成绩与物理成绩的相关性分析

下面将进一步探究高中物理学优生、中等生、学困生这三个层次学生的物理成绩与数学的相关性，依然以靖江市某中学高二理科班750名学生的期中考试成绩为样本。

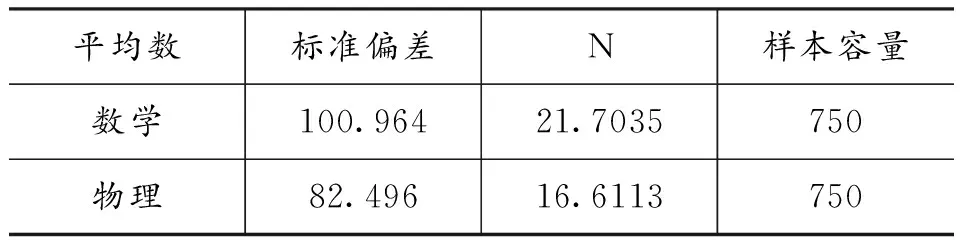
表4　数学与物理成绩的描述性统计

通过表4可以看出，物理的平均分为82.5(满分为100)，符合该校是重点高中的实际情况，此次物理考试试卷总体难度中等。根据图5物理成绩分布直方图，直观地显示出大多数学生的成绩在70-95分段，少数学生的成绩高于95分或者低于70分。基于此，定义此次物理考试成绩≥95分为学优生(共170人)，70分≤物理成绩<95分为中等生(共461人)，物理成绩<70分为学困生(共119人)。下面继续使用SPSS 22.0软件中皮尔森(Pearson)简单相关系数分层次进行数学与物理成绩的相关性分析。

图5　靖江市某校高二理科生期中物理成绩分布直方图

观察比较表5、表6和表7得知，物理学优生的数学与物理成绩皮尔森(Pearson)简单相关系数r=0.241，物理中等生数学与物理成绩皮尔森(Pearson)简单相关系数r=0.411，物理学困生数学与物理成绩皮尔森(Pearson)简单相关系数r=0.570。出乎意料，高中物理成绩越优异，与数学相关性系数越小，物理学困生的成绩与数学成绩相关性大。

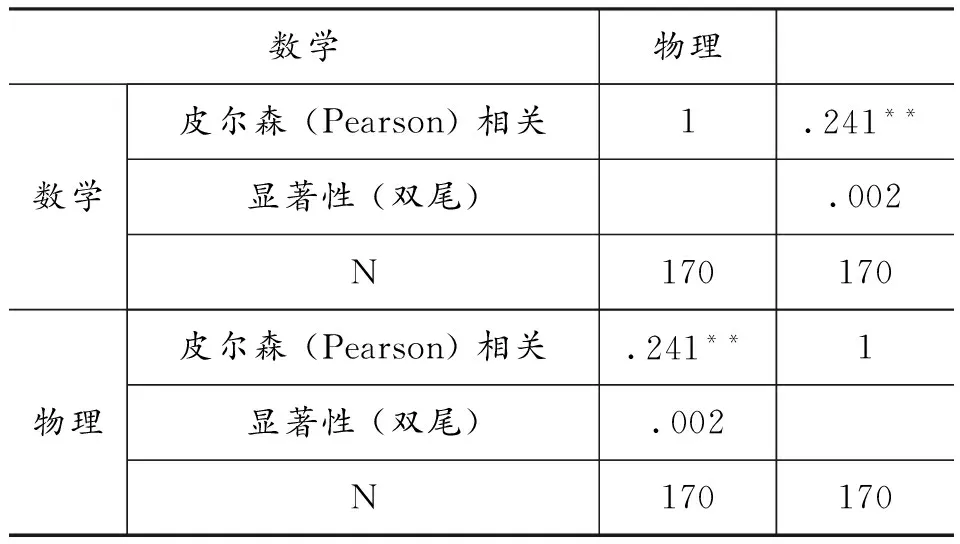
表5　物理学优生成绩与数学成绩的相关系数表

注：相关性在显著性水平α=0.01上，**表示P<0.01

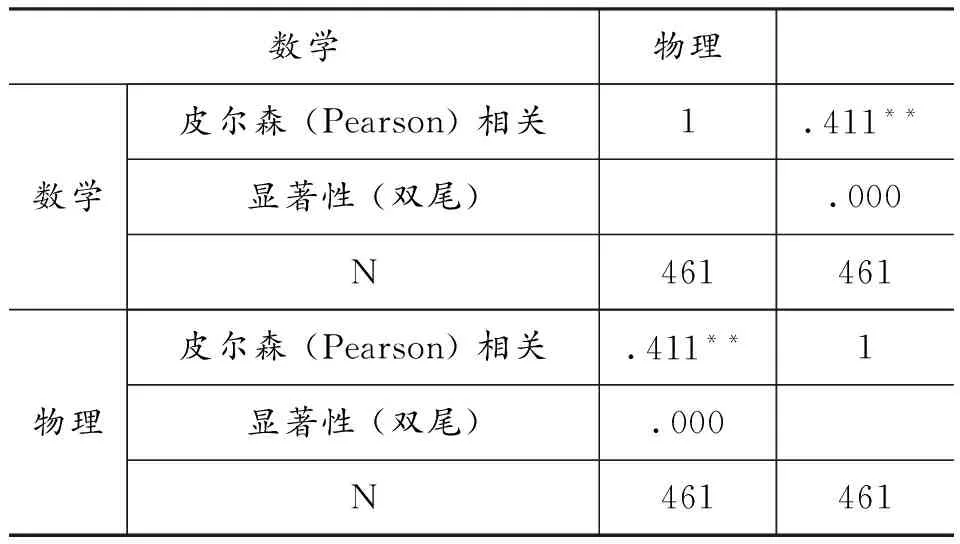
表6　 物理中等生成绩与数学成绩的相关系数表

注：相关性在显著性水平α=0.01上，**表示P<0.01

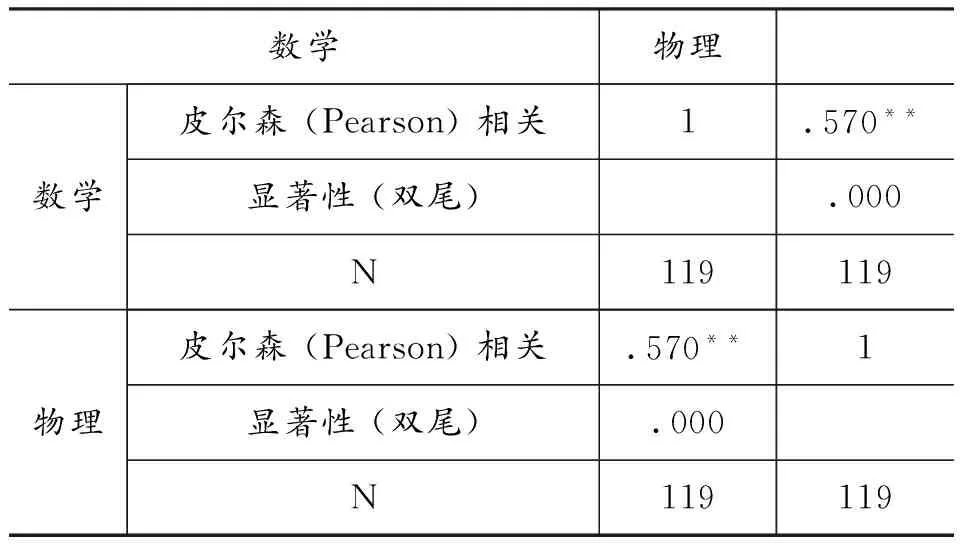
表7　物理学困生成绩与数学成绩的相关系数表

注：相关性在显著性水平α=0.01上，**表示P<0.01

通过对学生进行物理成绩分层与数学成绩的相关性分析，统计结果反映出物理学优生的物理成绩不仅仅与数学成绩有关，与其他能力因素也有关系；而对于物理学困生，其在物理学习中的表现与数学知识欠缺有很大关系。

六、讨论

通过对江苏省近5年物理高考试卷应用知识点的分布情况统计，发现解方程或不等式、解析几何与向量这3个数学知识点的运用较多。结合具体的物理高考大纲知识点内容与要求，解方程或不等式属于数值运算，是解决带有数量物理题目的必备过程。物理解题过程中，根据题中所给条件和以前学到的物理公式，将题中所提到的物理因素之间的关系用算式表达出来，通过列方程的方式解出未知值。物理题目中也经常有不等关系的问题，如要使物体加速运动，至少需要多少拉力？电灯的功率至多为多少，电路才不会发生短路现象？所以，列出不等式是求解的重要步骤。解析几何与向量在物理高考热点、难点——力学、电磁学、运动的题目条件分析中考点较多，对物体的受力分析、电磁场分布等都有所涉及，解析几何在数学高考中也是难度中等偏上的题目。

其实，除了这些具体的数学知识点，一些数学思想方法也很重要，它们能训练学生的思维能力，是寻求问题答案的有效途径。金宜友(2006)结合高中物理课堂实例，在“自由落体与函数模型的构建”中指出：数学模型能够客观地描述物理现象[8]；林慧芳(2005)提出，数形结合与物理学习紧密相连[9]，它能将复杂的问题简单化、抽象的问题具体化。关于数学思想方法的研究，可以结合课堂教学进一步开展。

利用皮尔森(Pearson)简单相关系数发现，与语文、英语相比，数学对物理成绩的影响最大，高中数学与物理成绩呈显著正线性相关。陈雨田(2005)结合自身16年的物理一线教学经验与几万人的数据检验分析，同样得出数学与物理成绩呈正线性相关。根据数学知识点在高考物理试卷中的分布，不难解释数学与物理的紧密联系。数学与物理同属于理科，都需要理性地去看待问题，数学先于物理学习，是因为数学能力能给学生学习、理解物理提供基础；物理实验观察得出结论定律依托于数学的思想方法，学生解决物理题目要学会灵活运用数学技巧方法。

在已经得出高中数学与物理成绩呈正线性相关后，依据物理成绩对学生进行分层：物理学优生、中等生、学困生，利用皮尔森(Pearson)简单相关系数得出数学成绩对学困生的物理成绩影响最大，其次是中等生，最后是学优生。这个结果是出乎意料的，经过仔细思考，物理成绩优异者不仅数学成绩优异、理性思维能力强，其他方面能力也很突出，比如做事细心、有钻研精神、观察能力强；而物理学困生的数学成绩往往在初中就很薄弱，这对他们物理学习、理解概念、课后习题带来了很大障碍。所以，在物理基础薄弱的班级，老师讲解物理题目时应适当解释答题过程中用到的数学知识，而在物理强化班，老师讲解主要集中于解题思路，解答详细过程可以减少。

七、结论

通过以上分析，本研究的主要结论如下：

首先，高中数学知识点在物理学习中有多方面的运用，其中解方程或不等式、解析几何、向量这3个数学知识点的运用较多。

其次，高中数学成绩与物理成绩呈现显著的正线性相关，且线性相关性高于语文、英语学科。

第三，高中物理学困生受数学成绩影响最大，物理学优生受数学成绩影响最小。

[1][3]梁树森.物理学习论[M].广西教育出版社,1996：123.

[2] 余雷.物理学创新思维[M].贵州民族出版社，2004：5.

[4] 王明高. 数学思维在物理教学中的应用[J]. 湖南科技学院学报, 2006, 27(11):297-298.

[5] 朱坤燕. 浅析数学方法在物理教学中的应用体现[J]. 才智, 2015(36).

[6] 陈雨田. 高中生的物理学习与数学学习相关性研究[D]. 华中师范大学, 2006.

[7] 张金宝, 李晓晓, 阴国恩. 中学生物理学科问题分类表征层次的研究[J]. 心理与行为研究, 2015, 13(2):266-270.

[8] 金宜友, 宋国强. 谈物理课外实验教学的尝试与探索[J]. 物理实验, 2006, 26(7):27-30.

[9] 林慧芳. 数学思想与方法和物理内容统一的探讨[J]. 物理教学探讨:中学教学教研专辑, 2005, 23(4):51-52.

(责任编辑：申寅子)

The Quantitative Research on the Effect of Mathematics on Physical Achievement in High School

ZHAO Yang

(DepartmentofCurriculumandInstruction，EastChinaNormalUniversity,Shanghai200062，China)

Mathematics and physics both belong to science department, there is certain correlation between them, what effect on physics achievement of high school mathematics is objective existing. On the basis of interpreting subject characteristics and the college entrance examination syllabus, taking the college entrance examination paper of physics in nearly five years of Jiangsu Province as the first sample, a senior high school students’ achievement in Jingjiang as the second sample, the paper analyses the effect of mathematics through quantitative on physics achievement in high school and compares the effect in different levels of students. The result shows: there are many mathematics knowledge used in physics learning in high school, the solution of equation or inequality, analytic geometry and vector three mathematical knowledge points are the most; the result of mathematics and physics has significant positive linear correlation, which is higher than that of Chinese and English; the correlation between mathematics and physics achievement in underachievers is highest, while achievers have the lowest.

high school physics achievement; mathematical method; correlation analysis; quantitative research

2016-04-26

赵阳,(1992- )，女，江苏扬州人，上海华东师范大学课程与教学系在读硕士研究生；研究方向：数学教育。

G40-03

A

1005-5843(2016)07-0036-07

10.13980/j.cnki.xdjykx.2016.07.007