3步光伏最大功率点跟踪算法

石季英，薛 飞，秦子健，凌乐陶

（天津大学电气与自动化工程学院，天津 300072）

3步光伏最大功率点跟踪算法

石季英，薛 飞，秦子健，凌乐陶

（天津大学电气与自动化工程学院，天津 300072）

光伏阵列的P-U特性曲线在局部阴影的情况下会呈现多个极值点，传统算法容易陷于局部极值，智能算法追踪耗时过多.在研究两类算法的基础上，提出一种基于扰动观察法和粒子群算法的3步最大功率点跟踪（MPPT）算法.该算法采用大步长扰动观察法缩小搜索范围并确定粒子数目；采用改进粒子群算法实现全局搜索寻找最优局部；采用逐步逼近的扰动观察法在最优局部内搜索最大功率点.仿真结果表明：该算法在均匀光照和局部遮阴情况下均能准确迅速地跟踪到最大功率点，相比于粒子群算法，追踪时间缩短35%,以上.

光伏阵列；多峰；局部阴影；3步最大功率点跟踪算法；改进的粒子群优化；扰动观察法

煤荒、电荒的出现以及对低碳生活的倡导使得人们对光伏发电十分青睐.光伏发电与传统能源发电相比，有着无动作部件、无噪声、清洁可再生等优势.光伏发电的核心问题是提高发电效率.其中，解决这个问题的重要手段之一就是最大功率跟踪（maximum power point tracking，MPPT）［1-4］，然而光伏阵列的P-U曲线是非线性的，尤其是在局部遮蔽的条件下，P-U曲线是多峰曲线，因此传统的MPPT算法（如扰动观察（P&O）法［5-7］、导纳增量法［8］和爬山法［9-10］等）就可能会陷入局部极值，无法跟踪到全局最大功率点［11-13］.而智能算法（如粒子群算法［14-16］、布谷鸟算法［17］、人工蜂群算法［18］等）虽然能实现多峰值情况下的最大功率跟踪，但由于其追踪时间过长，造成了一定的能量损失.文献［19-20］提出了一种2步最大功率点跟踪算法，先通过开路电压和短路电流来近似得到等效负载线，进而找到等效负载线上的最大功率点的领域，然后用传统MPPT进行最大值搜索，但当最大功率点位于负载曲线左侧，工作点暂时运行于0.9倍的阵列开路电压时，不能跟踪到最大功率点.

本文在深入研究多峰值P-U曲线特点以及扰动观察法和粒子群算法优缺点的基础上，提出一种基于扰动观察法和粒子群算法的3步MPPT算法（简称“三步法”）.该算法第1步采用定步长扰动观察法迅速找到第1个峰的大致位置，从而缩短了粒子群算法搜索的范围并且为粒子初始位置的设定找到依据；第2步采用改进粒子群算法实现全局搜索，当找到最优局部时停止搜索，且仅保留全局最优位置信息；第3步，在最优局部内采用逐步逼近扰动观察法寻找全局最大功率点，可以避免多个粒子在最终局部位置内的重复搜索，既节省时间，又能够保证搜索精度.该算法充分体现了扰动观察法的搜索快速性和粒子群算法的全局搜索能力，很好地实现了全局搜索和局部搜索的协调，从而使得该算法在收敛速度和收敛精度方面均表现优异.

1　光伏电池的多峰曲线分析

在光伏发电系统中，为提高输出效率，通常需要将光伏电池串联或者并联起来.考虑到热斑效应，一般在光伏电池两端反并联一个旁路二极管来防止其对光伏电池的损坏.旁路二极管的引入使得光伏阵列在局部阴影的情况下的P-U曲线出现多峰特性.本文以4×1的光伏阵列为例，对光伏阵列的多峰值特性进行Matlab/Simulink 仿真分析.光伏阵列结构如图1所示.

图1　光伏阵列结构Fig.1 Configuration of photovoltaic array

假定光伏阵列中每个组件的参数一致，仿真模型中各个组件的参数采用MSX-60的参数：短路电流Isc=3.8,A，开路电压Uoc=21.1,V，最大功率点电流Im=3.5,A，最大功率点电压Um=17.1,V.参考光照为1,000,W/m2，参考温度为25,℃.

为了分析串联光伏的多峰曲线特性，本文提出4种光照方案，分别为均匀光照、遮蔽情况1、遮蔽情况2和遮蔽情况3.温度设为25,℃时，4块光伏板A、B、C、D上的光照如表1所示.

表1　4种不同方案下的光照情况Tab.1 Irradiation of four kinds of case W/m2

由图2可以看出，当每块光伏板的光照不同时（即遮蔽情况3），P-U曲线峰值数目最多不超过串联光伏板的数目；未被遮蔽的光伏板越多，左侧未出现峰的区域越大.

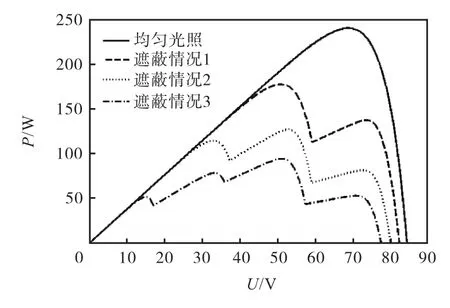
图2　光伏阵列P-U曲线Fig.2 ,P-U curves of photovoltaic array

2　3步MPPT算法

2.1扰动观察法

扰动观察法实现简单、追踪时间短，是传统寻优算法中最经典的一种.其原理为

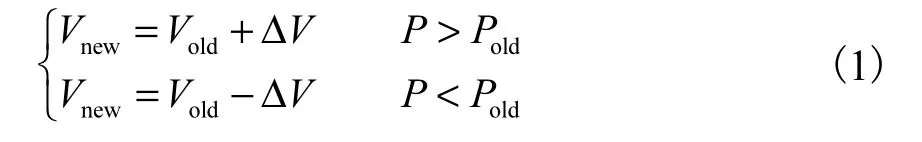
式中ΔV为扰动电压，当ΔV为固定值时，扰动观察法可以追踪单峰曲线的最大值，但会发生振荡.

2.2粒子群算法与改进的粒子群算法

粒子群算法是光伏MPPT智能算法中最经典的算法，原始粒子群算法中每个粒子有3个参数：即当前位置、速度和方向.每次迭代更新，粒子都是通过两个极值点来更新自身位置，第1个是粒子本身在当前时刻为止找到的最优解xpb,i，第2个是整个群体在当前时刻为止找到的最优解xgb.第k+1次迭代时第i个粒子速度和位置的更新方程为

式中：k为迭代次数；w为惯性权重；c1、c2为正常数，分别用于调整个体经验和群体经验的比重；r1、r2为（0，1）之间的随机数.

在原始粒子群算法中由于采用随机参数，步长大小也是随机的，存在步长不合适的情况即在非峰值区域或小峰值区域步长过小导致用时较多，在高峰值区域步长过大导致错过全局最大峰值点或者最终搜索到的点精度不够高，所以本文去掉随机参数r1和r2.

其次参数c1和c2的选择非常重要，固定值不能适应要求.如图3所示，假设x粒子为全局最优粒子，y粒子不停向其靠近，但在这个区域y粒子的适应值小于其个体最优值，使得步长变得很小，但从图中可以看出，这个区域属于功率值较低区域.为了减少在这个区域的功率损失，在（Pbest-Pi）/Pbest＞0.2时，认为该粒子处在功率较低区域，适当减少c1.

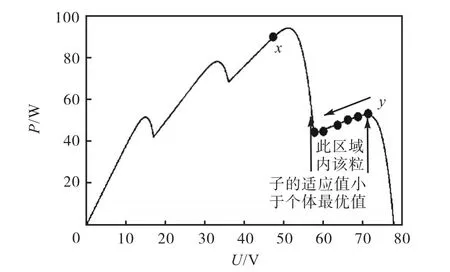
图3　粒子群算法局部示意Fig.3 Partial sketch map of PSO algorithm

2.33步MPPT算法介绍

三步法是在最大功率点追踪过程中发挥扰动观察法和粒子群算法各自优点的一种算法，其步骤如下.

步骤1 首先按照文献［14］，令Boost开关管占空比D=0，就可获取光伏阵列的开路电压Uarrayoc,.然后，采用较大步长的扰动观察法找到第1个峰的大致位置U1，并且根据找到的大致位置的电压和光伏阵列的开路电压差值，确定粒子数目N=［（Uarrayoc-U1）/Uoc］（［ ］表示向下取整）.根据第1个峰的大致位置U1（即第1个粒子的位置）确定其他粒子的位置，第i个粒子的初始位置为Ui=U1+（i-1）Uoc.

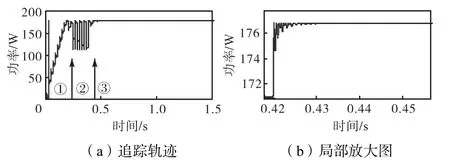
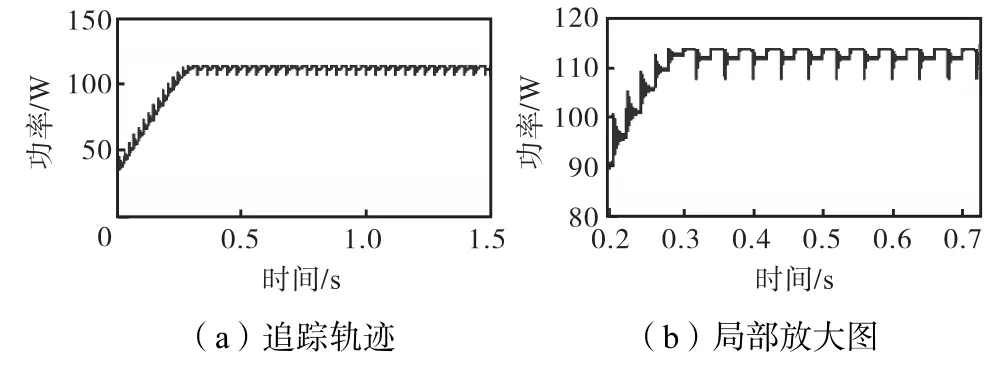
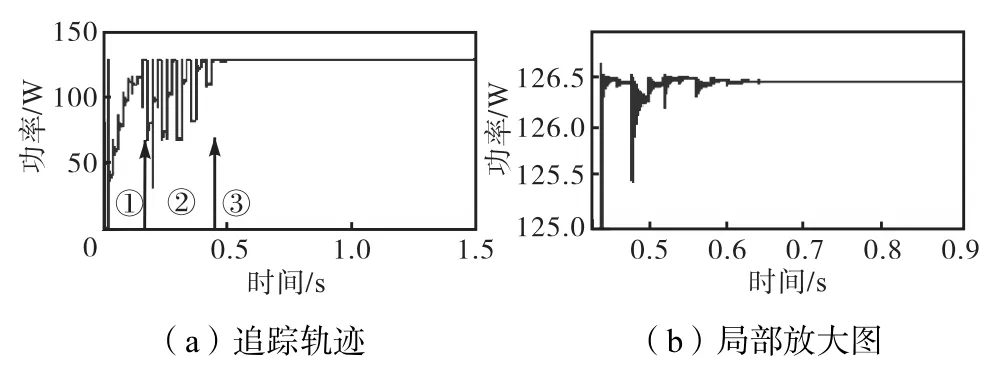
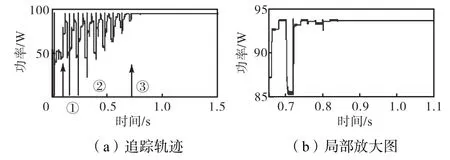
步骤2 采用改进粒子群算法，实现全局搜索，当找到最优局部时停止搜索；当最优位置与其余所有粒子位置距离的最大值dmax

在经过多次迭代后，所有粒子进入最优局部，最优粒子位置将非常接近全局最优值；而且在这个区域其他粒子的适应值都小于全局最优值，均会向其逼近，但过多粒子在这个区域迭代需要较多时间.

步骤3 采用逐步逼近的扰动观察法，将最优局部中的最优粒子位置作为扰动观察法的初始位置，以较小步长m进行扰动；当Pi+1＜Pi时，改变搜索方向并且以m/2为步长进行搜索；当Pi+1＜Pi再次满足时，再次改变搜索方向并且以m/4为步长进行搜索，依此类推，直到搜索到给定的精度范围，就认为搜索到了最大功率点.显然，逐步逼近的扰动观察法在搜索过程中是以指数形式提高的，从而很好地解决了跟踪速度和精度之间的矛盾.

如果采用粒子群算法（假设粒子数为4）在该最优局部继续追踪，则至少需要迭代4、5代才能达到收敛条件，也就是改变粒子位置16～20次，而采用逐步逼近的扰动观察法只需要1个粒子，最多更改5、6次位置，便可以达到同样的收敛效果.当光照突变时，即满足

则重启三步法.

3　仿真实验及分析

3.1仿真模型及参数选择

本文中使用图4所示的基于Boost电路的最大功率点跟踪系统，系统中光伏阵列采用图1所示的4×1光伏阵列.

图4　基于Boost电路的最大功率点跟踪系统Fig.4 Boost-based MPPT system

仿真模型中，C1=200,μF，C2=90,μF，L= 0.15,mH，Rload=40,Ω，Boost电路的开关频率为50,kHz.

3.23种算法参数选择

本文作为对比的扰动观察法的固定步长选为1.5,V；粒子群算法中，为了保证能够搜索到所有峰，粒子数目设为4（与串联光伏板数目相同），它们的初始位置依次设为0.8,Uoc、1.8,Uoc、2.8,Uoc和3.8,Uoc，w=0.2，c1=0.2，c2=0.35，最大限制速度为5，当粒子间的最大电压差值小于0.01,V时停止迭代；三步法第1步的扰动观察法的固定步长选为5，第2步中改进粒子群算法的最大限制速度为5，w=0.2，c2= 0.35，当粒子的适应值小于其个体最优值且（Pbest-Pi）/ Pbest＞0.2（较低功率区域）时，c1=0.05，其他情况下c1=0.2；第3步中m=0.5，当扰动步长m变为0.005时，停止搜索.

3.3仿真结果及分析

3.3.1均匀光照条件下的仿真

当光伏阵列在均匀光照条件下，即光照强度为1,000,W/m2，环境温度为25,℃时，其P-U曲线为单峰曲线（如图2所示）.分别采用扰动观察法、粒子群算法和本文提出的三步法对建立的光伏组件模型进行最大功率跟踪，三者的追踪曲线（P-t曲线）分别如图5～图7所示.

图5　均匀光照下P&O算法的追踪轨迹Fig.5 Trajectories for P&Oalgorithm under uniform condition

图6　均匀光照下PSO算法的追踪轨迹Fig.6 Trajectories for PSO algorithm under uniform condition

图7　均匀光照下三步法的追踪轨迹Fig.7 Trajectories for the three-step algorithm under uniform condition

由图5可以看出，在均匀光照下，P&O算法大约需要0.72,s找到最大功率点，但即使采用小步长，也会在最大功率点处振荡，如图5（b）所示，振荡差值约为1.52,W，造成了大量功率的损失.由图6可以看出，PSO算法需要大约0.86,s，其无法自动调节粒子数目，搜索时间较长.从图7可以看出，三步法只需要大约0.4,s，与粒子群算法相比，追踪时间缩短了53.49%,.三步法可以自动调节第2步的粒子数目，从图7（a）中可以看出第1步判断粒子数目为1，所以直接跳过第2步进入逐步逼近扰动观察法搜索，减少了搜索时间，降低了能量损失.

3.3.2遮蔽条件下的仿真

光伏阵列在遮蔽情况下，如表1中的遮蔽情况1、情况2和情况3，环境温度为25,℃.本文分别采用传统扰动观察法、原始粒子群算法和三步法对建立的光伏组件模型在3种不同的遮蔽情况下进行最大功率跟踪.3种方法的追踪曲线（P-t曲线）如图8～图16所示.

图8　遮蔽情况1下P&O算法的追踪轨迹Fig.8Trajectories for the P&O algorithm under shaded condition 1

图9　遮蔽情况1下PSO算法的追踪轨迹Fig.9Trajectories for the PSO algorithm under shaded condition 1

图10　遮蔽情况1下三步法的追踪轨迹Fig.10Trajectories for the three-step algorithm under shaded condition 1

在遮蔽情况1下，一块光伏板被遮蔽，其P-U曲线如图2所示，具有2个峰.由图8（a）可以看出情况1下扰动观察法追踪到了最大功率点，但在最大功率点处振荡，如图8（b）所示，振荡功率差值约为1.23,W，造成大量能量损失.由图9可以看出，粒子群算法大约需要1.04,s.由图10可以看出，三步法大约需要0.46,s，与粒子群算法相比，追踪时间缩短了55.77%,.三步法第2步只需要2个粒子，减少了搜索时间.

图11　遮蔽情况2下P&O算法的追踪轨迹Fig.11 Trajectories for the P&O algorithm under shaded condition 2

图12　遮蔽情况2下PSO算法的追踪轨迹Fig.12 Trajectories for the PSO algorithm under shaded condition 2

图13　遮蔽情况2下三步法的追踪轨迹Fig.13 Trajectories for the three-step algorithm under shaded condition 2

图14　遮蔽情况3下P&O算法的追踪轨迹Fig.14Trajectories for the P&O algorithm under shaded condition 3

图15　遮蔽情况3下PSO算法的追踪轨迹Fig.15Trajectories for the PSO algorithm under shaded condition 3

图16　遮蔽情况3下三步法的追踪轨迹Fig.16Trajectories for the three-step algorithm under shaded condition 3

在遮蔽情况2下，2块光伏板被遮蔽，其P-U曲线如图2所示，具有3个峰.由图11可以看出情况2下，扰动观察法陷入局部峰值点，这个局部峰值为114.1,W，而全局最大峰值为126.4,W，光伏系统输出功率为最大功率值的90.2%,，造成大量功率损失.由图12可以看出，粒子群算法需要大约1.25,s才能收敛.由图13可以看出，三步法仅需要大约0.58,s就能够追踪到最大功率点，与粒子群算法相比，追踪时间缩短了60.78%,，在第2步中有3个粒子，减少了搜索时间.

在遮蔽情况3下，3块光伏板被遮蔽，其P-U曲线如图2所示，具有4个峰.由图14可以看出，扰动观察法陷入局部峰值点，此局部峰值为51.51,W，而全局最大峰值为93.88,W，光伏系统输出功率仅为全局最大功率值的54.87%,，造成了大量功率损失.由图15可以看出，粒子群算法需要大约1.32,s才能收敛.由图16可以看出，三步法收敛大约需要0.84,s，与粒子群算法相比，追踪时间缩短了36.36%,，第2步需要4个粒子，对于最复杂的情况3，第1步对减少时间几乎没有影响，但三步法比粒子群算法用时缩短0.48,s，可以看出改进的粒子群算法和第3步起到缩短收敛时间的作用.

纵向比较扰动观察法，在遮蔽情况1下，虽然追踪到最大功率点，但会在最大功率点附近振荡；在遮蔽情况2和情况3下，扰动观察法均陷入局部极值，造成大量能量损失，其不具备在遮蔽情况下的最大功率点追踪能力.纵向比较粒子群算法，在遮蔽情况1、2和3下其追踪所用时间分别为1.04,s、1.25,s和1.32,s，由此可以看出遮蔽情况下，峰的数目越多，粒子群算法用时越多，但由于无法调节数目其用时差距不是很大.纵向比较三步法，在遮蔽情况1、2和3下其所用时间分别为0.46,s、0.58,s和0.84,s，可以看出被遮蔽的比例越低，在第1步中缩小的搜索范围越大，需要粒子数目越少，用时会大幅缩短.

4　结　论

（1） 本文分析了均匀光照和遮蔽情况下串联光伏阵列的输出功率特性，结果表明光伏阵列输出功率点的峰值个数最多是串联数，且未被遮蔽的光伏板越多，左侧不出现峰的区域越大.

（2） 本文提出的算法在遮蔽情况下和无遮蔽情况下都能快速地追踪到最大功率点.

（3） 本文提出的三步法相比于粒子群算法，追踪时间缩短35%,以上，可以看出在遮蔽情况下和无遮蔽情况下三步法均更具优势.

［1］ Guerrero J M，Blaabjerg F，Zhelev T. Distributed generation：Toward a new energy paradigm［J］. IEEE Transactions on Industrial Electronics Magazine，2010，4（1）：52-64.

［2］ Liserre M，Sauter T，Hung J Y. Future energy systems：Integrating renewable energy sources into the smart power grid through industrial electronics［J］. IEEE Transactions on Industrial Electronics Magazine，2010，4（1）：18-37.

［3］ Jung D，Ji Y，Park S，et al. Interleaved soft-switching boost converter for photovoltaic power-generation system［J］. IEEE Transactions on Power Electronics，2011，26（4）：1137-1145.

［4］ Esram T，Chapman P L. Comparison of photovoltaic array maximum power point tracking techniques［J］. Ranaon on Nrgy Onvron，2007（2）：439-449.

［5］ Femia N，Petrone G，Spagnuolo G，et al. Optimization of perturb and observe maximum power point tracking method［J］. IEEE Transactions on Power Electronics，2005，20（4）：963-973.

［6］ Piegari L，Rizzo R. Adaptive perturb and observe algorithm for photovoltaic maximum power point tracking［J］. IET Renewable Power Generation，2010，4（4）：317-328.

［7］ Abdelsalam A K，Massoud A M，Ahmed S，et al. High-performance adaptive perturb and observe MPPT technique for photovoltaic-based microgrids［J］. IEEE Transactions on Power Electronics，2011，26（4）：1010-1021.

［8］ Safari A，Mekhilef S. Simulation and hardware implementation of incremental conductance MPPT with direct control method using Cuk converter［J］. IEEE Transactions on Industrial Electronics，2011，58（4）：1154-1161.

［9］ Alajmi B N，Ahmed K H，Finney S J. Fuzzy-logiccontrol approach of a modified hill-climbing method for maximum power point in microgrid standalone photovoltaic system［J］. IEEE Transactions on Power Electronics，2011，26（4）：1022-1031.

［10］ Xiao W，Dunford W G. A modified adaptive hill climbing MPPT method for photovoltaic power systems［C］// The 35th Annual Power Electronics Specialists Conference（PESC）. Aachen，Germany，2004：1957-1963.

［11］ Kaushika N D，Gautam N K. Mismatch losses and time to failure of solar PV arrays［C］//Proceedings of International Solar Energy Society Meeting. Adelaide，Australia，2001：1681-1686.

［12］ Shimizu T，Hirakata M，Kamezawa T，et al. Generation control circuit for photovoltaic modules［J］. IEEE Transactions on Power Electronics，2001，16（3）：293-300.

［13］ Mishima T，Ohnishi T. A power compensation strategy based on electric double layer capacitors for a partially shaded PV array［C］ //International Conference on Power Electronics & Drive Systems. Singapore，2003：858-863.

［14］ 朱艳伟，石新春，但扬清，等. 粒子群优化算法在光伏阵列多峰最大功率点跟踪中的应用［J］. 中国电机工程学报，2012，32（4）：42-48. Zhu Yanwei，Shi Xinchun，Dan Yangqing，et al. Application of PSO algorithm in global MPPT for PV array［J］. Proceedings of the CSEE，2012，32（4）：42-48（in Chinese）.

［15］ Miyatake M，Toriumi F，Endo T，et al. A novel maximum power point tracker controlling several converters connected to photovoltaic arrays with particle swarm optimization technique［C］//European Conference on Power Electronics & Applications. Aalborg，Demmark，2007：1-10.

［16］ 刘艳莉，周 航，程 泽. 基于粒子群优化的光伏系统MPPT控制方法［J］. 计算机工程，2010，36（15）：265-267. Liu Yanli，Zhou Hang，Cheng Ze. MPPT control method of PV system based on PSO［J］.Computer Engineering，2010，36（15）：265-267（in Chinese）.

［17］ Ahmed J，Salam Z. A maximum power point tracking（MPPT）for PV system using Cuckoo search with partial shading capability［J］. Applied Energy，2014，119（12）：118-130.

［18］ Sundareswaran K，Sankar P，Nayak P S R，et al. Enhanced energy output from a PV system under partial shaded conditions through artificial bee colony［J］. IEEE Transactions on Sustainable Energy，2015，6（1）：198-209.

［19］ Kobayashi K，Takano I，Sawada Y. A study on a two stage maximum power point tracking control of a photovoltaic system under partially shaded insolation conditions［J］. Electrical Engineering in Japan，2003（4）：2612-2617.

［20］ Kobayashi K，Takano I，Sawada Y. A study of a two stage maximum power point tracking control of a photovoltaic system under partially shaded insolation conditions［J］. IEEE Transactions on Industry Applications，2006，153（4）：39-49.

（责任编辑：孙立华）

Three-Step MPPT Algorithm for Photovoltaic Systems

Shi Jiying，Xue Fei，Qin Zijian，Ling Letao
（School of Electrical Engineering and Automation，Tianjin University，Tianjin 300072，China）

Multiple local maximums would be exhibited on the power-voltage characteristic curve of photovoltaic array，under partially shaded conditions.Conventional maximum power point tracking（MPPT）algorithms tend toget into local maximum，while the intelligent MPPT methods would spend much time in tracking.After studying the conventional and intelligent MPPT algorithms，a three-step MPPT algorithm based on perturbation and observation（P&O）algorithm and particle swarm optimization（PSO） algorithm was proposed in this paper.The three-step algorithm used P&O method with large step to narrow the search range and determined the number of particles，used PSO algorithm to achieve global search and to find the global optimal local，and used approximation P&O methodto find the global maximum power point in the optimal local.Simulation results proved the three-step algorithm can track the global maximum power point quickly and accurately under uniform condition as well as partially shaded conditions.The tracking time of the three-step MPPT algorithm is 35%, or more shorter than that of PSO algorithm.

photovoltaic（PV）array；multi-peak；partial shading；three-step maximum power point tracking（MPPT）algorithm；improved particle swarm optimization（PSO）；perturbation and observation（P&O） method

TK448.21

A

0493-2137（2016）05-0485-06

10.11784/tdxbz201505040

2015-05-06；

2015-07-03.

国际科技合作专项资助项目（2013DFA11040）；国家自然科学基金资助项目（61172014）；天津市自然科学基金重点资助项目（12JCZDJC21300）.

石季英（1959—），男，博士，副教授.

石季英，tjuxf1010@126.com.

网络出版时间：2015-11-11. 网络出版地址：http://www.cnki.net/kcms/detail/12.1127.N.20151111.1801.008.html.