基于遗传算法与Weibull模型的软土地基沉降预测

林达，陈志坚

（河海大学地球科学与工程学院，南京211100）

基于遗传算法与Weibull模型的软土地基沉降预测

林达，陈志坚

（河海大学地球科学与工程学院，南京211100）

根据软土地基的物理力学性质，普遍认为其沉降过程近似为反“S”形曲线。为了研究软土地基沉降过程以及预测最终的沉降量，本文运用这一结论，综合考虑了软土地基沉降的阶段性发展与生物成长模型的数学性质，选用了适应性较高的Weibull成长曲线模型，利用遗传算法在处理岩土类多参数以及非线性问题上的独特优势，通过对3个不同地区具有代表性的软土地基所选工程实例的沉降观测数据进行拟合。结果表明：软土地基经过加载后其沉降发展一般会经历一个类似于生物成长规律的发生、发展、逐步稳定的三个阶段，且反“S”形的成长模型能够反映其沉降的阶段性；采用Weibull模型能够根据反弯点的位置来判断对应时刻所处的沉降阶段，有利于控制施工以及加载过程；运用遗传算法能够很好地解决非线性岩土工程反分析问题，以残差平方和作为目标函数，根据残差值分析可知，用遗传算法得到的Weibull软土地基沉降模型具有较高的精度。

软土地基；Weibull模型；遗传算法；沉降拟合

0引言

软土是在静水或非常缓慢的流水环境中沉积的，具有含水量高、孔隙率高，渗透性弱以及高压缩性等性质淤泥质土的总称，它广泛分布于我国沿海和内陆的海相、河湖相软弱黏土层地区。随着我国高速路网、桥梁以及高层建筑的兴建，必然会遇到软土地基的处理问题。而软土基础沉降则是表征其承载性能的重要指标，也是控制工程施工过程的关键。

对于软土地基的沉降过程，经前人总结，其沉降-时间曲线近似为反“S”形［1-2］。因此，有学者提出用成长类型曲线来对其沉降过程进行拟合，进而用于预测基础的沉降［3-5］。

由于用曲线拟合对桩基础沉降进行预测需要利用到桩基础沉降的前期数据，而沉降的观测数据往往非线性以及离散程度较高，很难直接对其过程进行直接拟合。因此，本文使用遗传算法来进行拟合，通过遗传算法来确定拟合模型的相应参数，进而得到模型的解［6-7］。

1沉降预测模型

1.1模型的数学性质及适用性

目前用于分析基础沉降的成长模型主要有Gompertz模型，Logistic模型［8］和Weibull模型。其中：

Gompertz模型的表达式为：

Logistic模型的表达式为：

Weibull模型的表达式如下：

式中：参数a，b，c，k均为正数；t为时间。

由表达式（1）-（3）可知，成长模型曲线具有以下特点：①不通过坐标原点性。即处于0时刻，沉降值不为0，且其值等价于瞬时沉降。②单调性。对模型进行求导即可知，导数恒大于0，模型是单调递增的。③有界性。即当时间t取无穷大时，S为定值。④满足软土地基固结度条件。固结度表达式有：

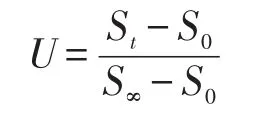
将模型带入固结度表达式，即可知t=0时刻，固结度的值为0。t取无穷大时，固结度的值为1。

模型的这些特点都能很好的反应出软土地基沉降的过程。一般情况下，软土地基的沉降过程可以分为三个阶段：瞬时沉降、固结沉降和次固结沉降。由于瞬时沉降的存在，沉降曲线不通过原点。三个阶段可以概括为：

①施加荷载初期，土体处于弹性阶段，沉降几乎是线性增加；

②随着不断增大荷载，土体处于弹塑性阶段，沉降量和沉降速率不断增加；

③当停止增加荷载时，由于土体具有流变性，沉降量仍然继续增加，但沉降速率不断减小，并且最终沉降值趋于稳定。

这三个阶段，与自然界中生物的成长规律非常的相似，即与上述模型的本质上具有一致性。

综上所述可知：成长曲线能够做到很好地反映地基沉降发生、发展、逐步稳定的阶段性规律，两者的变化过程性质是一致的。为了更好的利用沉降观测资料预测软土地基的最终沉降，可以把成长曲线模型引入沉降的预测中。

1.2Weibull模型的优势

对于沉降预测成长曲线模型的选取，本文采用Weibull模型［9］，因为对之前两种模型的分析以及众多实例可知，它们虽然呈反“S”形状，但无法反映施工工艺和软基处理过程的影响，且由于对实测样本反弯点的特殊依赖性，单纯的采用Logistic模型或是Gompertz模型是不容易进行有效预测的，而Weibull模型则能够摆脱对实测样本反弯点的依赖［4］。此外，Weibull模型具有4个参数，且每个参数有其具体的物理意义，对于我国沿海沉积环境所处的复杂地质条件，有必要考虑多个参数对沉降的影响。

Weibull模型中各参数的物理意义如下：a为地基基础最终沉降；b为基础瞬时沉降；k为地基基础加荷因子，取决于施工的过程，加荷速度越快，则k的取值也越大；c与地基基础所处的地质环境有关，为一综合影响因子。不同的工程，其对应的参数也不同，此外，Weibull模型还考虑了基础初始沉降不为零的情况，因此该模型具有可推广性。

1.3Weibull模型的可简化性

即根据模型的参数意义可知，在经历过瞬时沉降过后的基础沉降-时间过程可以视为经过原点的反“S”形曲线，因此，在这种情况下，b值可以取为0。

2遗传算法

遗传算法是一种仿生全局优化算法，以模仿生物的遗传进化为原理，通过选择、交叉与变异等操作机制，使种群中个体的适应性不断提高，对于任意形式的目标函数和约束，无论是线性的还是非线性的，离散的还是连续的都可处理。由于软土地基沉降的研究性质是非线性，不均匀，多变量的，因此遗传算法在处理此类问题中有其独特的优势［6-7］。

针对Weibull模型的遗传算法思路如下［10］：

2.1编码方法与种群空间

为了编码、解码操作简单以及交叉、变异等遗传操作便于实现，一般采用搜索能力比较强的二进制编码，以Weibull模型参数a，b，k，c作为相应的决策变量，根据精度采用5位二进制编码，初始种群空间随机生成即可。

2.2适应度函数

确定适应度函数，建立优化模型，确定出目标函数的类型及其数学描述形式或量化方法。根据本文研究的桩基础沉降，构造优化模型的方法为界限构造法：

若目标函数为最大值问题：

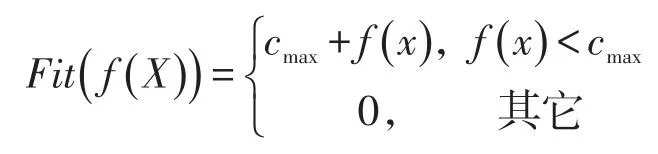
cmax为f（x）的最大估计值。

若目标函数为最小值问题：

cmin为f（x）的最小估计值。

所以根据Weibull模型的表达式所构建的目标函数为目标函数最小值问题，即：其中n为观测样本数量，St为t时刻实测沉降值，Sw为t时刻的Weibull模型沉降预测值。

2.3选择算子和选择操作

计算群体中个体解码后的适应值，通过适应值来确定个体选择概率，然后通过选择概率，采用轮盘赌选法进行选择。解码公式为：

式中，［XlXr］——参数最小、最大值；L——参数编码长度；k——二进制串对应的实数值。

2.4交叉率及交叉操作

对于二进制编码，常用的交叉方法有：单点交叉、多点交叉和均匀交叉等。这里采用的是单点交叉，即随机产生一个交叉位，在交叉位互换2个进行交配的染色体（图1）。

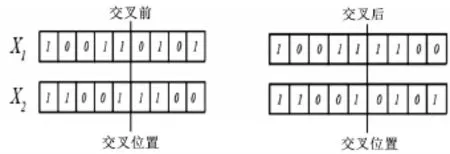
图1　单点交叉示意Figure 1 A schematic diagram of one-point crossover

2.5变异率及变异操作

采用二进制变异法，即将所编码中的某些点，用其他等位点进行替换，形成新的个体（图2）。

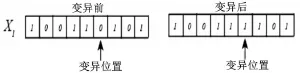
图2　变异替换示意Figure 2 A schematic diagram of variation substitution

2.6编程建立优化模型

即按照遗传策略，运用所选定的选择、交叉和变异算子作用于群体，生成下一代群体。通过判断群体性能是否满足某一指标或完成预定迭代次数来得到最终的结果。本文采用的指标为最大代数500。

3实例分析

实例1选取文献［8］中的宁杭高速公路工程实例。该工程软土地基分布广泛，采用了等载预压、粉喷桩、土工格栅等方法来控制沉降量。现取东南大学交通学院在溧阳段NH标K95+520观测点得到的沉降观测资料。该测点地基处理采用预压加载方式，路堤填土分8级进行，累计填土高度为5.70 m。依据此工程中前80 d的沉降观测数据，利用遗传算法对其进行沉降拟合及预测的最优解收敛代数为132，可得拟合模型表达式为：

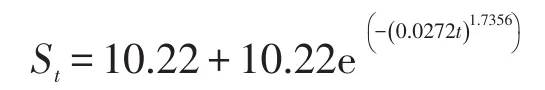
由此可得到表1以及图3反应沉降的拟合以及最终沉降的预测情况。

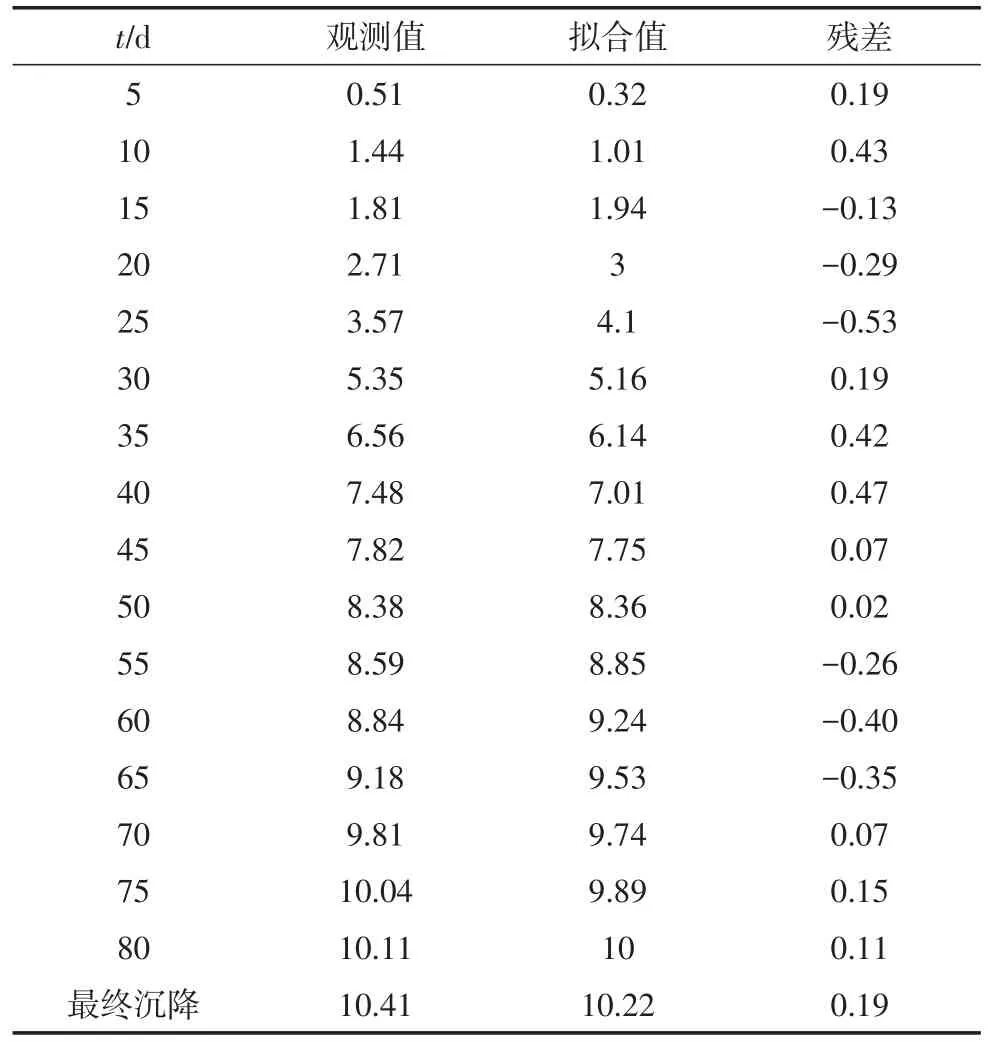
表1　K95+520测点观测值与拟合值mmTable 1 Observed and fitted values of survey station K95+520

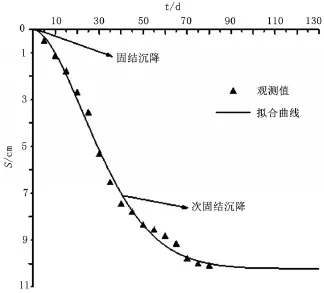
图3　K95+520测点观测值与拟合曲线Figure 3 Observed value and fitting curve of survey station K95+520

由实例1的结果可知，K95+520测点的预测最终沉降量误差为1.8%，b的值即为0，即瞬时沉降阶段在施工开始之前就已经完成，残差值较小，且越来越稳定，反映整体拟合效果较好。

实例2选取文献［7］中的珠江三角洲某拟建工程。该工程位于滨海地区，地基条件为深厚的流塑态海相沉积的淤泥，且上部覆盖有厚约6 m的填土。此类软土地基，在上部建筑荷载下将会产生很大的沉降，为了控制施工过程以及研究其沉降变化规律，对其进行沉降拟合预测。选择在场区内设置的1号观测点，沉降观测从开始填回0.5 a起，历时3 a。遗传算法最优解收敛代数为43，可得如表2、图4以及拟合模型为：

由图4可知整条沉降拟合曲线完全位于Weibull模型的反弯点之后，这符合观测数据的采集时间处于工后沉降的事实。且最终沉降量误差为3%，满足工程精度的要求。b值等于0，施工过程不包含瞬时沉降阶段。

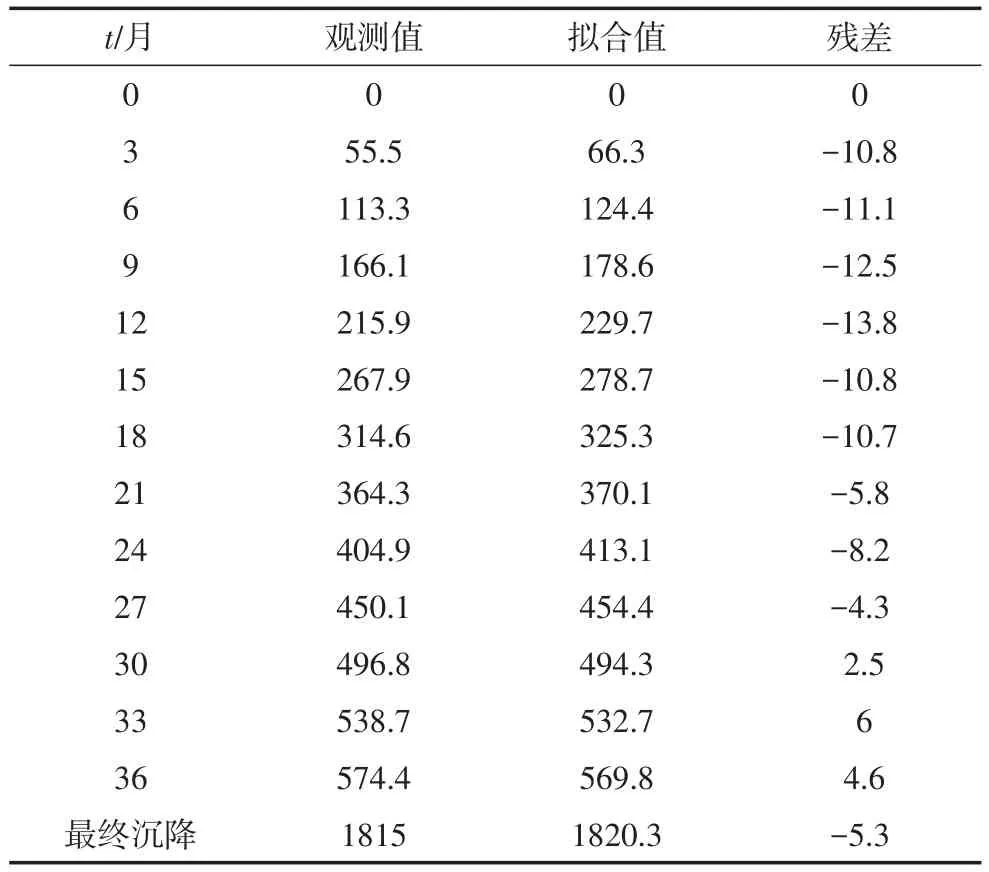
表2　1号测点沉降观测值与拟合值mmTable 2 Settlement observed and fitted values of survey station No.1

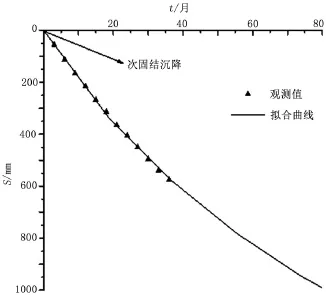
图4　1号测点观测值与拟合曲线Figure 4 Observed value and fitting curve of survey station No.1

实例3，苏通大桥桥位区属长江积平原的新长江三角洲。河床覆盖层深厚，第四系是以浅海、滨海、潟湖、河、湖相为主，总厚度在200～300 m，主要由淤泥质黏土、粉质黏土、粉土、粉砂、细砂、中粗砂等组成。

大桥的群桩基础沉降和监测从承台浇筑完一直持续到通车运营后，Weibull曲线模型几乎可以拟合出全过程的基础沉降过程。由于拟合要求对沉降数据必须是等时间间距的，而实际工程监测中的到的数据并不是等间距的，因此本文选取位于大桥4号墩的静力水准点S5在225 d内得到的沉降时间序列值进行插值得到的结果，来进行基础的沉降模拟。遗传算法最优解收敛代数为63，可以得到表3、图5以及拟合模型表达式如：

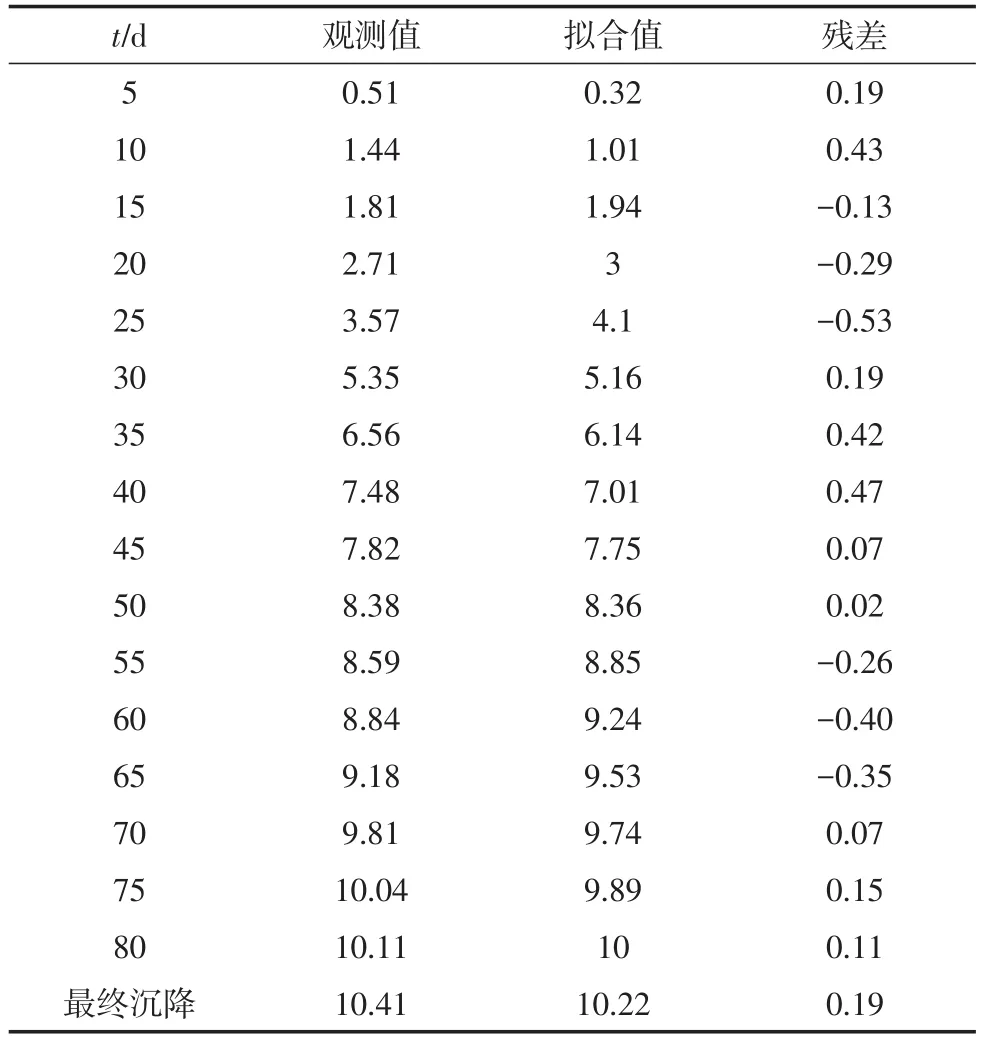
表3　S5静力水准点沉降观测值与拟合值Table 3 Settlement observed and fitted values of static benchmark S5mm

由实例3的结果可知，S5测点的预测最终沉降量误差为3.7%，b的值即为0时刻的观测值，误差为1.3%，残差值反映整体拟合效果较好。

实例当中，若基础沉降监测是在瞬时沉降（第一阶段）结束后进行的，在模型当中对应的b值（瞬时沉降）通常都为0，即曲线经过原点，这与实际情况是相符合的。并且从模型的a值（最终沉降）即能直接得到沉降的一个最终值，对于施工场地的稳定性以及安全性具有直接的参考价值。此外，根据Weibull模型拟合出的曲线上反弯点的位置，可以判断出某个时间段所发生的沉降所属于哪种沉降（阶段），这对于控制加荷速率以及施工过程都能起到一定的作用。

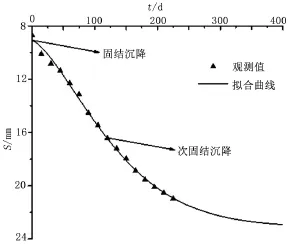
图5　S5静力水准点观测值与拟合曲线Figure 5 Observed value and fitting curve of static benchmark S5

总结以上实例，各观测时间点的残差值都较小，并趋于稳定，说明模型的拟合效果较好，且其误差都能够满足工程精度的要求。各实例均是不同地理位置软土地基问题类型的典型代表，经过遗传算法拟合的Weibull曲线模型，都能够较好的拟合沉降时间过程以及预测最终沉降值。因此该方法用于软土地基沉降拟合以及沉降预测，是切实可行的。

4结语

本文基于遗传算法的Weibull模型对软土地基的沉降进行研究，得到了以下结论：

①软土地基经过加载后其沉降发展一般会经历一个类似于生物成长规律的发生、发展、逐步稳定的三个阶段。且通过实例中的观测值散点图可知，反“S”形的成长模型能够反映软土地基的沉降过程。

②利用Weibull模型来建立拟合关系，通过对三个不同地区代表性的软土地基沉降数据进行拟合可知，无论在拟合效果还是最终沉降的预测结果，都与实测数据相吻合，说明了该方法的科学性以及适用性。

③通过拟合出的Weibull曲线，可以根据反弯点的位置来判断对应时刻所处的沉降阶段，这对于控制施工以及加载过程具有一定的参考价值。

④用遗传算法能够很好地解决此类非线性岩土工程反分析问题，以残差平方和作为目标函数，根据计算实例所得表中的残差值可知，用遗传算法得到的Weibull软土地基沉降模型的精度较高。

［1］宰金珉，梅国雄.全过程的沉降量预测方法研究［J］.岩土力学，2000，20（4）：322-325

［2］梅国雄，宰金珉，殷宗泽，等.沉降-时间曲线呈“S”型的证明［J］.岩土力学，2004，25（1）：20-22.

［3］涂许杭，王志亮，梁振淼，等.修正的威布尔模型在沉降预测中的应用［J］.岩土力学，2005，26（4）：621-623.

［4］王伟，卢廷浩.基于Weibull曲线的软基沉降预测出模型分析［J］.岩土力学，2007，28（4）：803-807.

［5］汪洋，余湘娟，姜健.软基沉降预测模型的比较分析与应用［J］.水利与建筑工程学报，2012，10（4）：127-130.

［6］夏江，严平，庄一舟，等.基于遗传算法的软土地基沉降预测［J］.岩土力学，2004，25（7）：1131-1134.

［7］刘勇健.遗传算法在软土地基沉降计算中的应用［J］.工业建筑，2001，31（5），39-41.

［8］赵明华，龙照，邹新军.基于Logistic曲线和Gompertz曲线的最优组合沉降预测模型及其应用［J］.公路交通科技，2007，24（12）：1-9.

［9］朱珉仁.Morgan-Mercer-Flodin模型和Weibull模型的拟合［J］.数学的实践与认识，2003，33（1）：1-4.

［10］雷英杰，张善文，李继武，等.MATLAB遗传算法工具箱及应用［M］.西安：西安电子科技大学出版社，2004.

Soft Soil Foundation Settlement Prediction Based on Genetic Algorithm and Weibull Model

Lin Da，Chen Zhijian
（School of Earth Science and Engineering，Hohai University，Nanjing，Jiangsu 211100）

According to soft soil foundation physical and mechanical properties，generally considered that its settlement process is approximate to an inverse“S”shaped curve.To study soft soil foundation settlement process and predict ultimate settlement，based on above mentioned cognition，comprehensively considered the mathematical nature of soft soil foundation settlement staged development and biological growth model，then selected high adaptable Weibull growth curve model.Using uniqueness of genetic algorithm on geotechnical multiparameter processing and nonlinear problems，carried out fitting for 3 different areas representative soft soil foundation project cases settlement observed data.The result has shown that soft soil foundation after loading，its settlement development will be generally experienced occurring，developing and gradually stabilizing 3 stages similar to biological growth；and the inverse“S”shaped growth model can reflect its staged settlement.Using Weibull model can judge corresponding time settlement stage based on bending point position，that helpful to control operation and loading process.Using genetic algorithm can solve nonlinear geotechnical engineering back analysis problems better.Taking the residual sum of squares as objective function，according to residuals analysis can know that the Weibull soft soil foundation settlement model from genetic algorithm has higher accuracy.

soft soil foundation；Weibull model；genetic algorithm；settlement fitting

TU447

A

10.3969/j.issn.1674-1803.2016.08.13

1674-1803（2016）08-0063-05

江苏省政策引导类计划（产学研合作，BY2015002-05）

林达（1993—），男，硕士研究生，地质资源与地质工程专业。

2015-12-23

责任编辑：樊小舟