某固体火箭发动机过载环境下内流场研究①

张卫平，杨　丹，熊永亮

(1.中国航天科工集团公司六院四十一所，呼和浩特　010010；2.华中科技大学 船舶与海洋工程学院，武汉　430074；3.华中科技大学 力学系，武汉　430074)



某固体火箭发动机过载环境下内流场研究①

张卫平1，杨丹2，熊永亮3

(1.中国航天科工集团公司六院四十一所，呼和浩特010010；2.华中科技大学 船舶与海洋工程学院，武汉430074；3.华中科技大学 力学系，武汉430074)

文中对某固体火箭发动机工作末期出现的压力振荡现象进行数值研究，采用大涡模拟对装药燃烧后期时刻进行数值模拟，得到了燃烧室内装药转角产生的旋涡脱落现象。通过对燃烧室内不同位置的流场参数进行监测，得到了由于旋涡脱落产生的压力振荡频率。同时，对发动机轴向过载工作条件进行了模拟，得到了过载条件对发动机内压力振荡的影响。结果表明，过载瞬间对发动机内部产生一个大幅压力脉冲，且发动机内不同位置处的影响是不同的，过载使得发动机尾部旋涡脱落的主频发生小幅度增大。最后对发动机头部装药结合进行优化，改进后的内流场旋涡强度得到大幅减小。

固体火箭发动机；不稳定燃烧；压力振荡；过载

0　引言

固体火箭发动机不稳定燃烧，又称振荡燃烧，是研制固体火箭发动机经常会遇到的一个具有挑战性的技术难题。其典型的特征是发动机内部工作压力-时间曲线不规则，进而使得发动机的推力振荡与设计要求不符，结构发生振荡等多种危害[1]。经过半个世纪的深入研究，人们对固体火箭发动机的不稳定燃烧取得了一些理论与经验性的共识。然而，随着发动机的多样化需求以及工作环境的恶化，目前又有越来越多的火箭发动机遇到不稳定燃烧的问题[2]。

通过对法国Ariane 5号发生不稳定燃烧的P230固体火箭助推器的大量研究，Dotson[3]等提出旋涡脱落是引起固体火箭发动机压强振荡的主要原因，旋涡脱落的频率与发动机的固有声振频率耦合，激发了发动机内流动的不稳定性。最初有关声涡耦合机理的描述是由Flandro和Jacobs[4]一起提出的，他们在1973年首次指出旋涡脱落有可能激发大型分段式固体火箭发动机燃烧室的声模态产生共振，从而引起压强振荡。流体中的旋涡既是一种扰动，也是释放声能的流动声源，流场中大量存在的旋涡与发动机内部声振之间的复杂非线性耦合作用，也是近年来发动机不稳定燃烧研究的热点问题。Space Shuttle RSRM,Titan IV SRMU 与Ariane 5号助推器P230发动机等一些大型分段式固体火箭发动机，由于燃烧室凸出的障碍物或者装药的突扩结构，在其下游诱导出强剪切流作用的旋涡脱落。发动机内的旋涡脱落主要可归结为转角旋涡脱落[5]、障碍物旋涡脱落[5]以及表面旋涡脱落[6-7]三类。Dotson[3]针对发生推力振荡的Tian IV SRMU发动机，通过试验测量建立了旋涡从形成、脱落、碰撞、声反馈的4步模型。利用数值计算[8-11]，人们也捕捉到了发动机内的旋涡脱落，结合流场与声场的能量交换机理来研究涡/声耦合现象，并取得了一些结论，但目前对涡/声耦合机理的理解仍存在分歧。

特别是战术火箭通常燃烧室更短，不应轻易地认为发生了涡/声耦合。即使很长的战术火箭，基频也在150 Hz以上。涡的作用和声振的作用不容易使发动机达到极大振幅，涡声耦合是极难出现的。引起发动机不稳定燃烧的因素是多方面的，旋涡与外界干扰或者过载产生的发动机简单壳体振动响应及流动响应，也是有可能激发发动机不稳定燃烧的。因此，对发动机内旋涡流动进行研究，对深入理解发动机压力振荡具有重要意义，本文的主要研究内容为发动机内旋涡脱落现象。

另外，发动机在工作过程中，由于加速和机动性能改变等因素，不仅会影响总体内弹道性能以及产生局部烧蚀[12]，同时也会对内部压力振荡产生影响。本文针对发动机内旋涡流动现象，对某固体火箭发动机内流场进行数值模拟，并对该发动机加载前后瞬间进行对比，研究发动机发生纵向过载条件下的流动稳定性，目的是为了得到发动机过载条件对其内流场不稳定流动的影响。最后，通过改变装药结构，对比发动机尾部的旋涡强度。

1　流场数学模型与计算方法

通过大涡模拟方法求解可压缩Navier-Stokes方程组，对发动机内流场进行数值模拟，流场控制方程可通过对原始N-S方程进行空间滤波后得到。对于可压缩流动，引入密度加权平均(Favre)，可表示为

(1)

(2)

式中D为流场区域；G为滤波函数。

滤波函数定义如下：

(3)

式中V为计算单元的体积。

对N-S方程进行滤波后，得到控制方程如下：

(4)

(5)

(6)

式中“—”表示雷诺(Reynolds)平均；“～”表示密度加权平均。

分子粘性应力张量定义为

(7)

式中μ为动力粘度。

亚格子应力相表示为

(8)

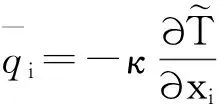
采用壁挂式本地涡粘性(Wall-adapting local eddy-iscosity,WALE)亚格子模型，在WALE模型中，涡粘度由式(9)计算：

(9)

Ls=min(kd,CϖV1/3)

本文选取发动机工作末期发生压力振荡的某一时刻进行数值计算，计算区域及边界条件设置如图1所示。图1中，同时给出了改进后的装药结构。发动机喷管网格见图2。计算中，分别选取发动机燃烧室内部沿轴线以及壁面位置进行数值监测，并对时域信号进行分析，监测点如图3所示。

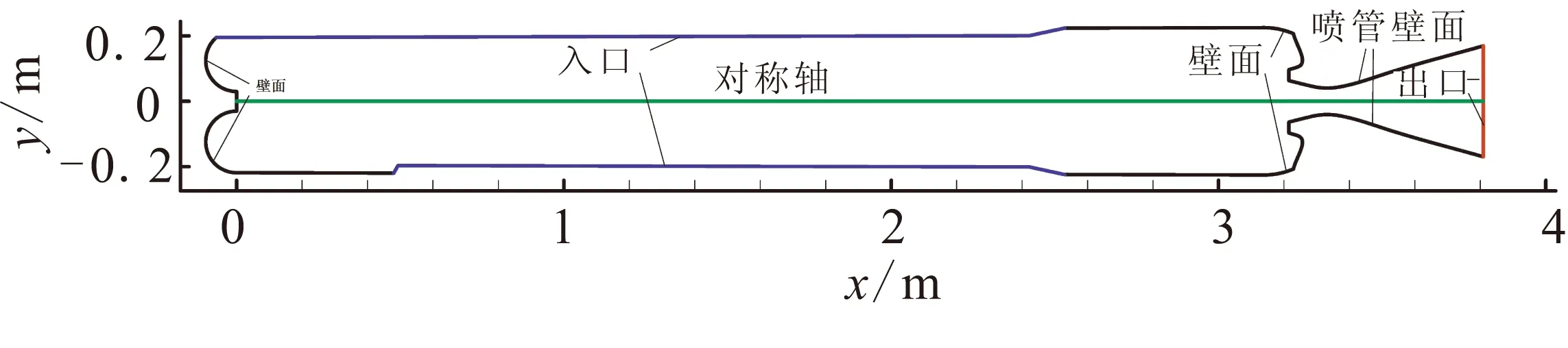
图1　某固体火箭发动机工作末期计算区域及相应边界条件(对称轴下侧为改进后装药)

图2　发动机喷管网格

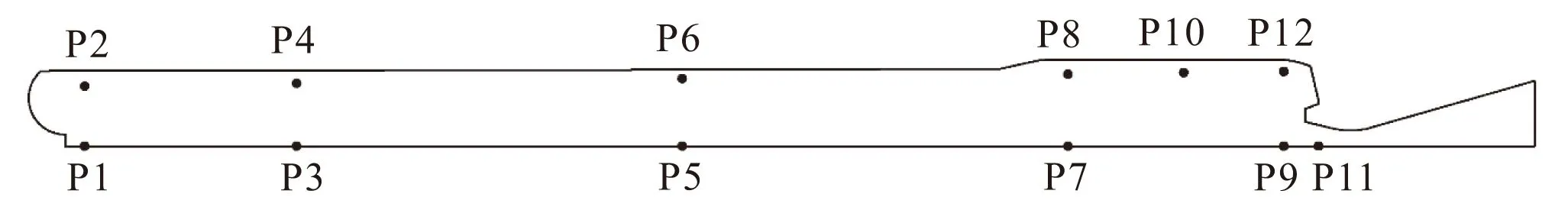
图3　发动机内各监测点位置

2　计算结果与讨论

2.1发动机无过载情况

图4所示为发动机内部的压力、马赫数与温度的瞬态结果，由于这些参数的空间脉动值相比总的压力、马赫数与温度是小量，因而在图4中观察不出小的空间脉动分布。总体上看，这些参数的结果分布与稳态计算的差别较小，图中所示的结果符合发动机内部流动的物理行为，燃气在燃烧室内积聚进行压力填充，通过喷管流出时燃气膨胀做功，压力在喷管中下降、马赫数升高、温度下降。

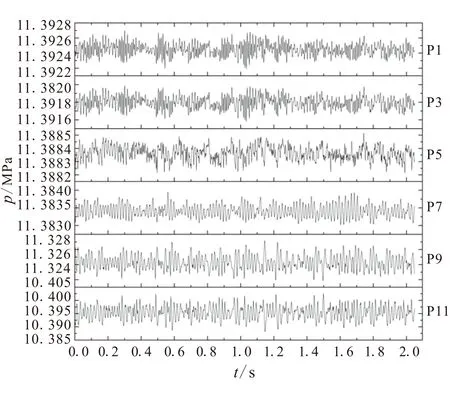
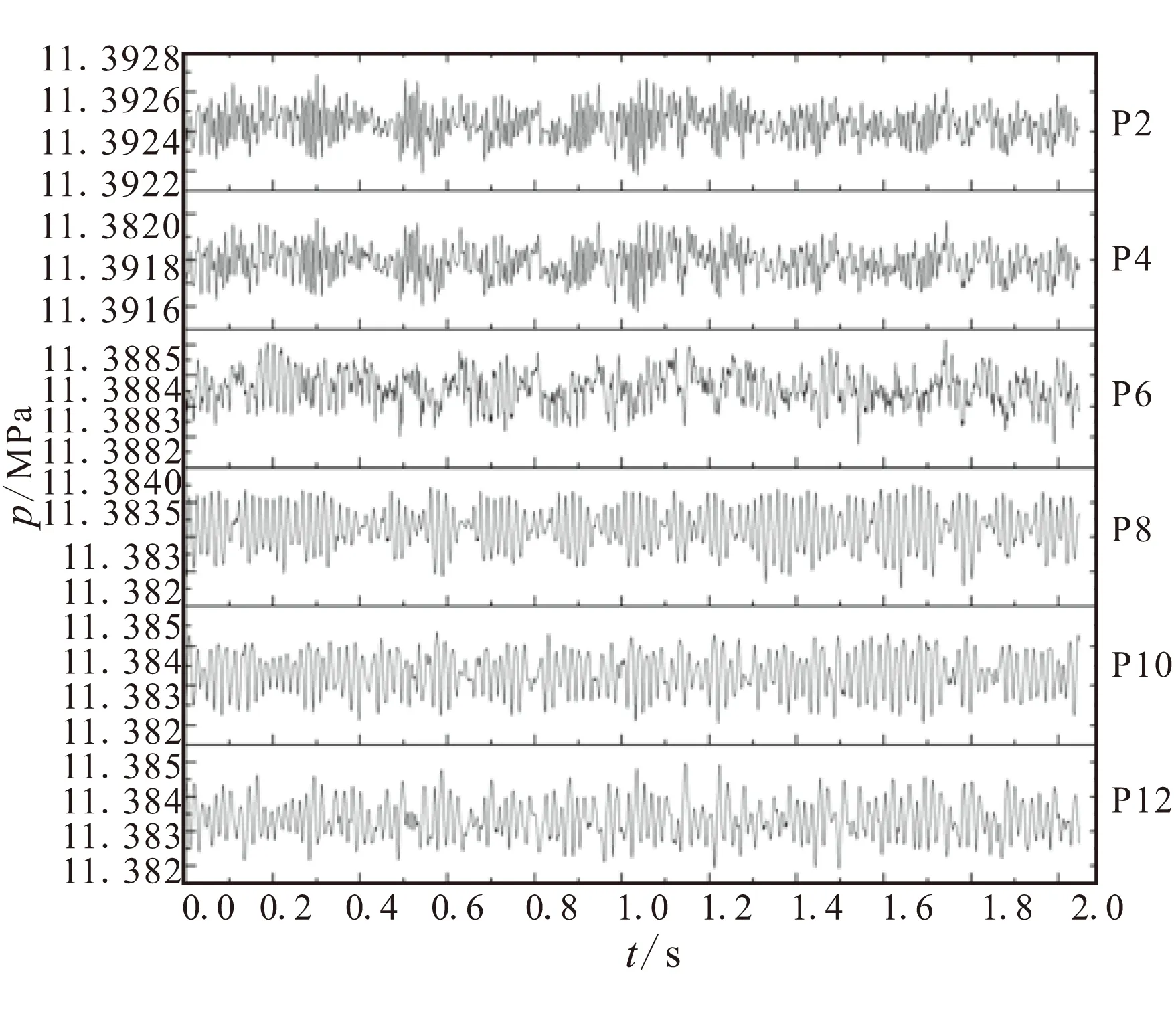
图5为监测点的压力随时间变化情况。

图4　发动机内部燃气的压力云图、马赫数云图与温度云图

(a)轴线上各监测点

(b)壁面附近各监测点

由于不同位置各点的脉动幅度不相同，为了显示清楚脉动的变化规律，各图纵坐标的幅度是不同的。通过脉动幅度来看，各点沿着发动机轴线方向，脉动幅度逐渐增加。在相同的轴线位置，靠近发动机头部部分，轴线与壁面处的脉动幅度相当，但在靠近喷管的发动机尾部，壁面处的脉动幅度要大于轴线处的脉动幅度。从总的压力脉动信号来看，脉动在几千帕的范围以内，且并不规则。

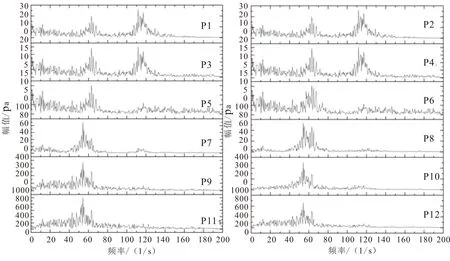
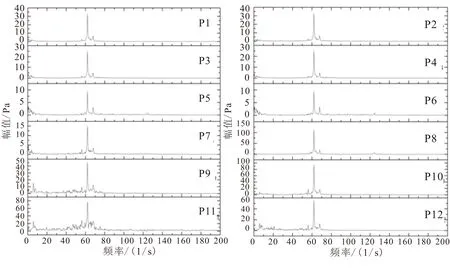
为了观测压力脉动的频率，图6给出了压力脉动的频谱。傅立叶变换的结果显示了压力脉动具有一系列的特征频谱，其中各点在60 Hz附近存在一个较为明显的特征频率。然而，该频率却并不固定，随各点的轴线位置不同，频率也有所变化，总的趋势是在发动机轴向上往喷管方向频率逐渐降低。

从各点的压力谱同样可观察到，靠近发动机头部位置，压力振荡幅值较小，轴线以及壁面位置处，其主频位于111.82 Hz，见图6中点P1～P4，而这一频率在到达发动机中部后消失。另外，发动机头部另一高频位置位于62.99 Hz处，与主频近似倍频关系，见图6中点P1～P6。随着监测点向喷管方向移动，压力主要振荡频率变为54.20 Hz，相对于这一频率，此时62.99 Hz的振荡幅值较小，见图6中点P7～P12，且此时倍频关系消失。除此之外，在低于20 Hz范围内，也有一系列低频存在，对于尾部各点，由于60 Hz左右的频率较强，这一频率的谱密度要弱许多。各图的纵坐标的变化范围也都不相同，总的趋势是发动机越往后，其幅值越大。

(a)轴线上各监测点　　　　(b)壁面附近各监测点

图7所示为各监测点的速度频域曲线。从图7中可看出，除了发动机头部的小幅度速度振荡频率与压力振荡频率不同以外，速度谱在发动机后半段同样捕捉到了主频为54.199 22 Hz的速度振荡，且速度谱在发动机壁面位置处，相对于轴线位置，其频谱较复杂，说明壁面处的扰动强于轴线处。从振荡幅值来看，靠近发动机喷管的壁面位置处，其振荡幅值高于轴线上的振荡幅值。

(a)轴线上各监测点　　　　(b)壁面附近各监测点

由于发动机装药结构存在转角，发动机内出现了转角旋涡脱落现象。图8为发动机内涡量在时间间隔为0.004 5 s的瞬态计算结果。由于喷管处流体的速度非常高，与喷管无滑移壁面之间形成极强的剪切流动，因而发动机内部最大涡量值出现在喷管壁面附近，但这些极强的涡被压缩在很小范围内，且随高速流动流出发动机，对燃烧室声腔影响最大的旋涡，还是在燃烧室内部。

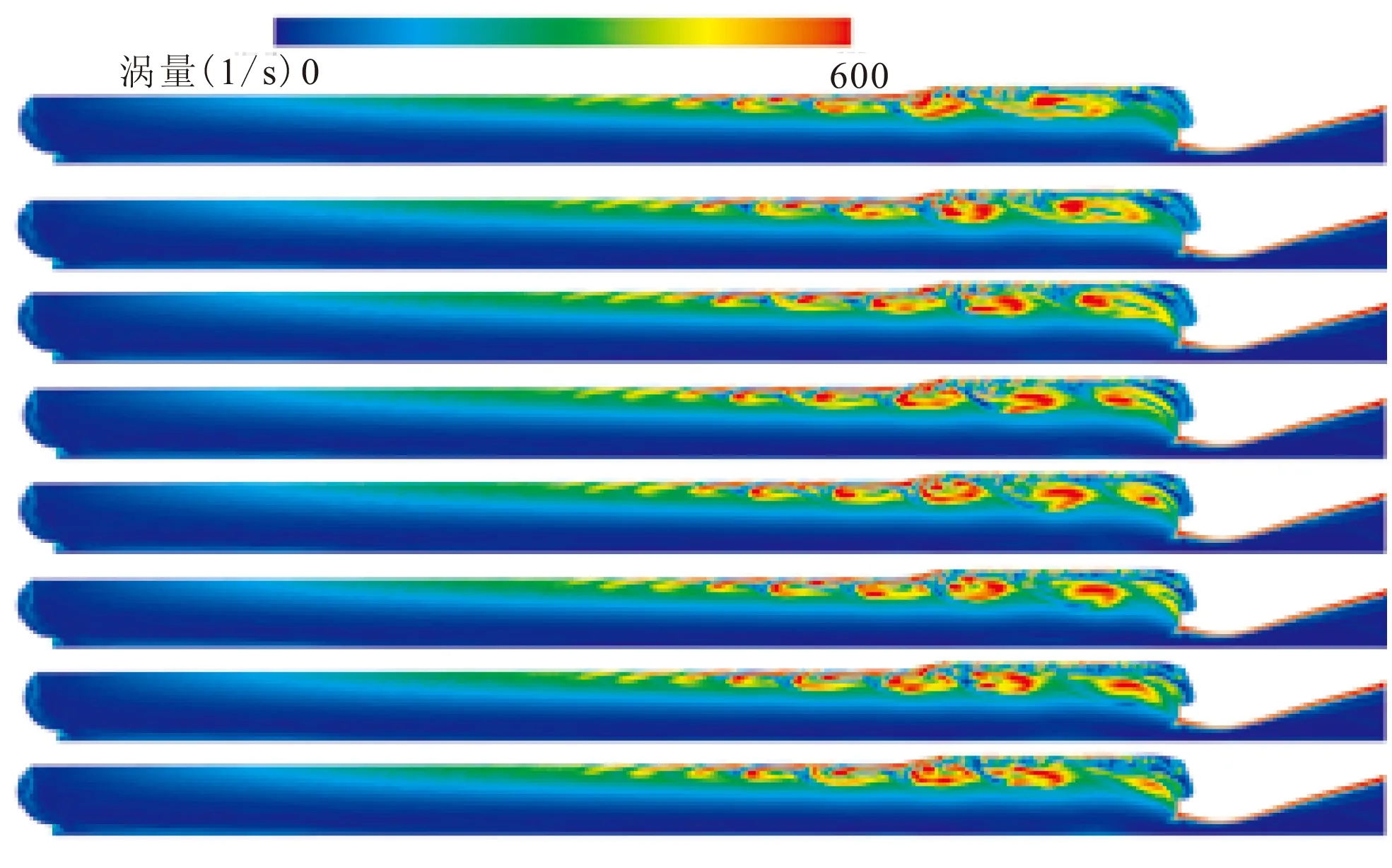
图8　发动机内瞬时涡量云图(时间间隔为0.004 5 s)

图8中，显示了涡量从0～600(1/s)的范围。可见，在装药尾部的突扩几何结构附近，产生了较复杂的流动结构，装药的转角结构使得此处流动发生分离，产生较强较大的旋涡，这里产生的旋涡在主流的作用下，向下游移动发生脱落，但图中脱落的涡在强度上受流体粘性影响，逐渐减弱，但其尺寸并没有缩小，甚至有所增长，这是由轴对称计算导致的湍流能量反向串级所造成的。结合图5～图7的压力时间曲线以及压力、速度的频谱可发现，发动机内转角位置脱落的旋涡并非均匀一致的，但其脱落的频率约为54.2 Hz。

另外，在突扩处下游靠近壁面处，也能观察到有数量较多、尺度较小的漩涡脱落，这些小涡会与几何扩张引起的大涡在轴对称计算情况发生合并。需要特别指出的是，在固体燃面附近剪切流动的强度是随空间变化的，越往下游剪切作用越强。由于当前计算方法的限制，燃面的无滑移壁面本质无法体现，实际的流量入口条件相当于采用了一个有滑移壁面，这很大程度地降低了此处涡的强度和数量。实际的燃面附近应比现在的计算结果产生更多更强的旋涡。

2.2轴向过载情况

为考察过载工作条件对发动机内流场的影响，在发动机内流场计算达到统计平衡态后，对流场施加23g的轴向过载条件，并对加载前后的流动情况进行对比。图9所示为发动机内各监测点的压力在加载条件下的变化情况。由图9可知，加载条件使得靠近发动机头部位置处的压力发生阶跃性下降，其压力下降幅度可达到约0.1 bar(见图9中P1～P4)。对于下降幅度较大的各点(如P1、P2)，其压力经过约0.2 s的振荡后，逐渐趋于稳定。随着监测点的位置向喷管喉部靠近，压力的下降幅度逐渐减小，而此时过载条件对压力的影响表现为压力类似脉冲信号的振荡，经过同样约0.2 s后，压力的平均值趋于稳定(见图9中P7～P10，P12)。监测点P11位于喷管收敛段，由图9中发现，过载对P11处压力的影响并不明显。

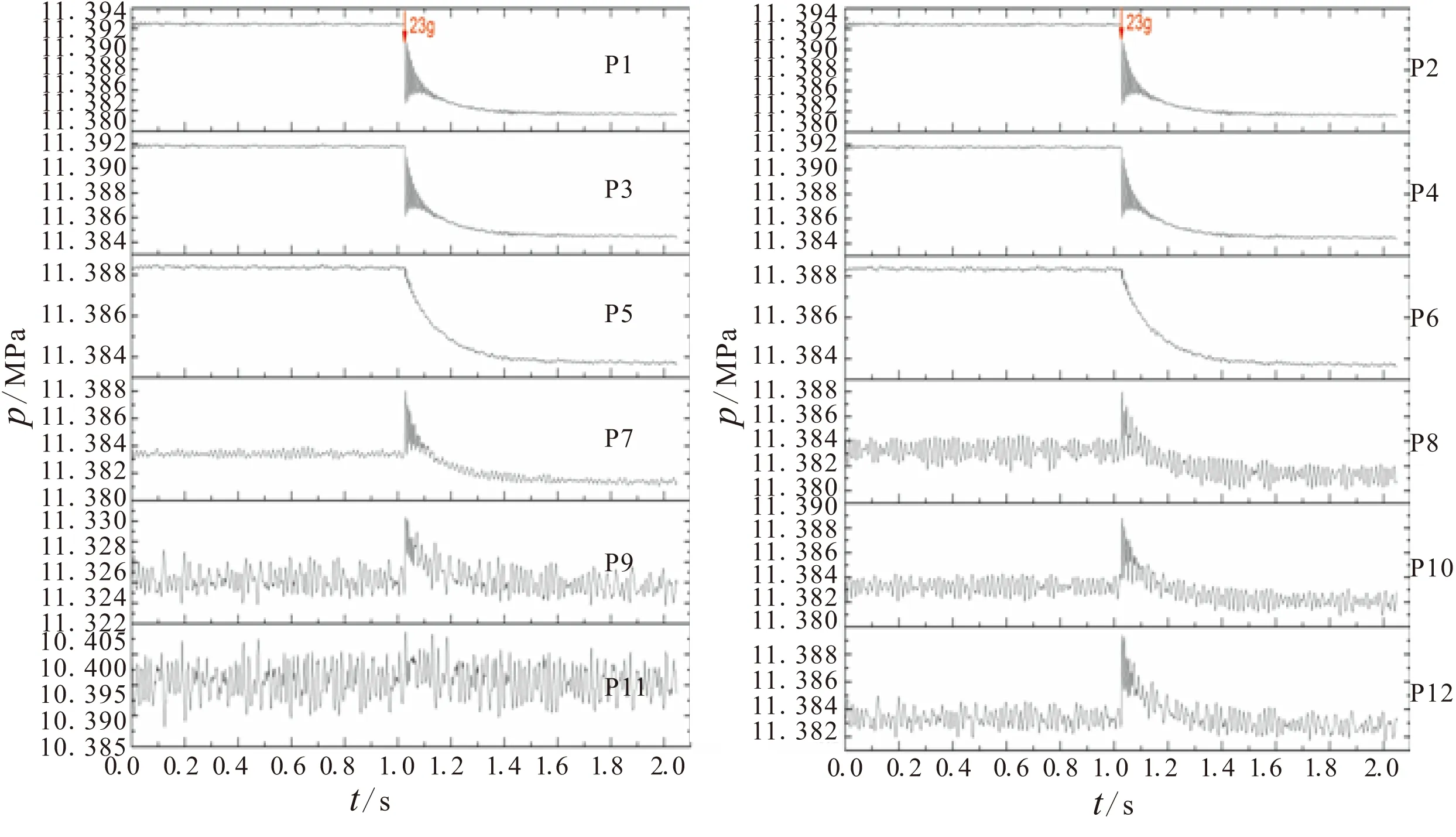
(a)轴线上各监测点　　　　(b)壁面附近各监测点

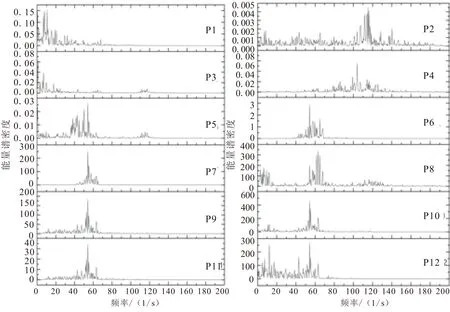
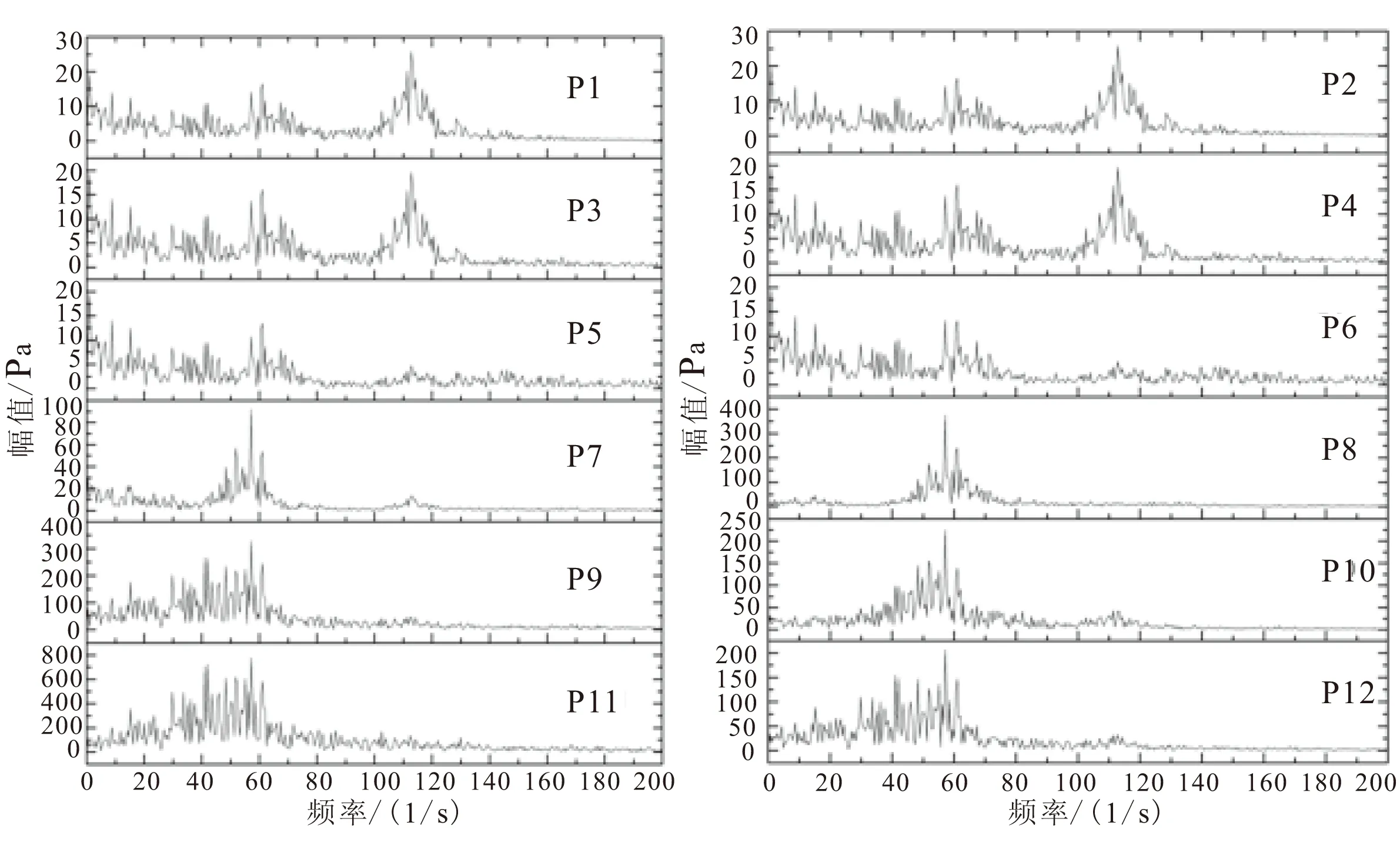
图10为加载后，发动机内流场趋于稳定后的压力频域曲线，与加载前的压力频谱相比，此时发动机头部主频位置是112.79 Hz，其次为61.04 Hz，见图10中点P1～P4。同样，随着监测点的位置逐渐向喷管移动，其压力振荡主频下降为57.13 Hz，见图10中点P5～P12。通过对比可发现，发动机轴向过载对靠近头部位置的压力小幅度振荡的影响较小，而对于靠近发动机尾部受旋涡脱落影响较强的各点，过载条件使得低于60 Hz的振荡频宽增加，且使得靠近喷喉位置的振荡幅度有较大地下降。

图11对比了轴向过载分别为11.5g、23g、34.5g时，发动机内不同位置处的压力时间曲线。从图11中可发现，加载瞬间压力振荡随加载强度的增大而增大。

(a)轴线上各监测点　　　　(b)壁面附近各监测点

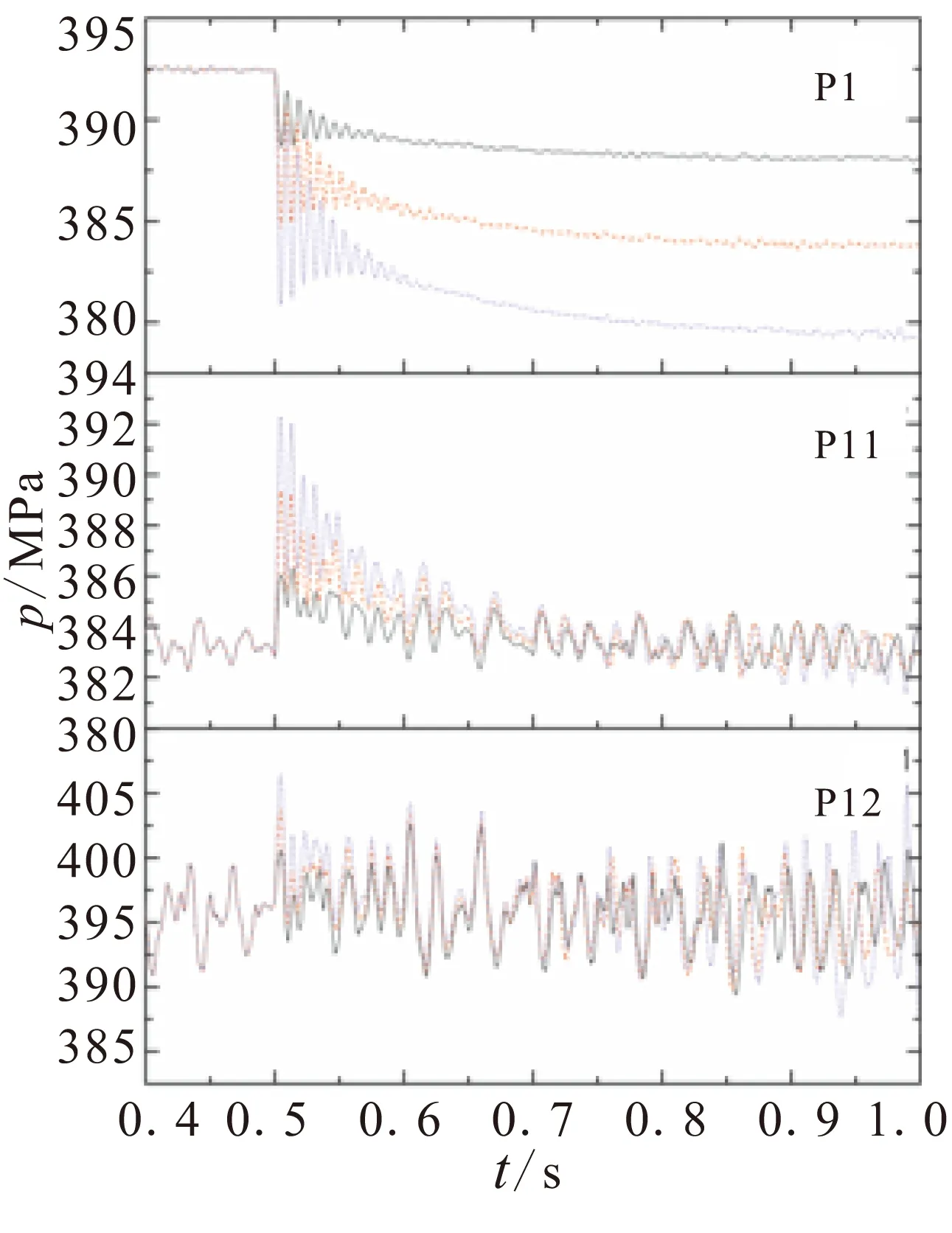
图11　不同加载情况下监测点P1、P11、P12位置处的压力-时间曲线(图中黑色实线为11.5 g，红色点划线为

2.3改变装药计算结果

图12和图13所示为改变装药结构发动机工作末期燃烧室内各监测点压力谱以及燃烧室涡量场，新装药方式的头部采用快燃药，则在其头部出现了一个更大的空腔，燃面则相应的减小，因而改变装药后的燃烧室压力要更加小，马赫数与温度场同改变前差别较小。图12中的压力脉动频谱显示各点的主频均为62 Hz，对比图6中装药修改之前的频谱曲线，此时燃烧室内各点的主频单一，相对于主频，其他频率并不明显。

图13显示，改变装药的涡量被大大地降低，而且涡的尺寸明显减小，呈现了较弱的流动不稳定特征。这可能是因为此时加质与改进前相比要更加少，剪切作用更弱。当然，也有全尺寸实验总结得出的结论指出，分段发动机中头部空腔促进发动机不稳定，因而对头部空腔的影响，也值得更进一步细致地研究。

(a)轴线上各监测点　　　　(b)壁面附近各监测点

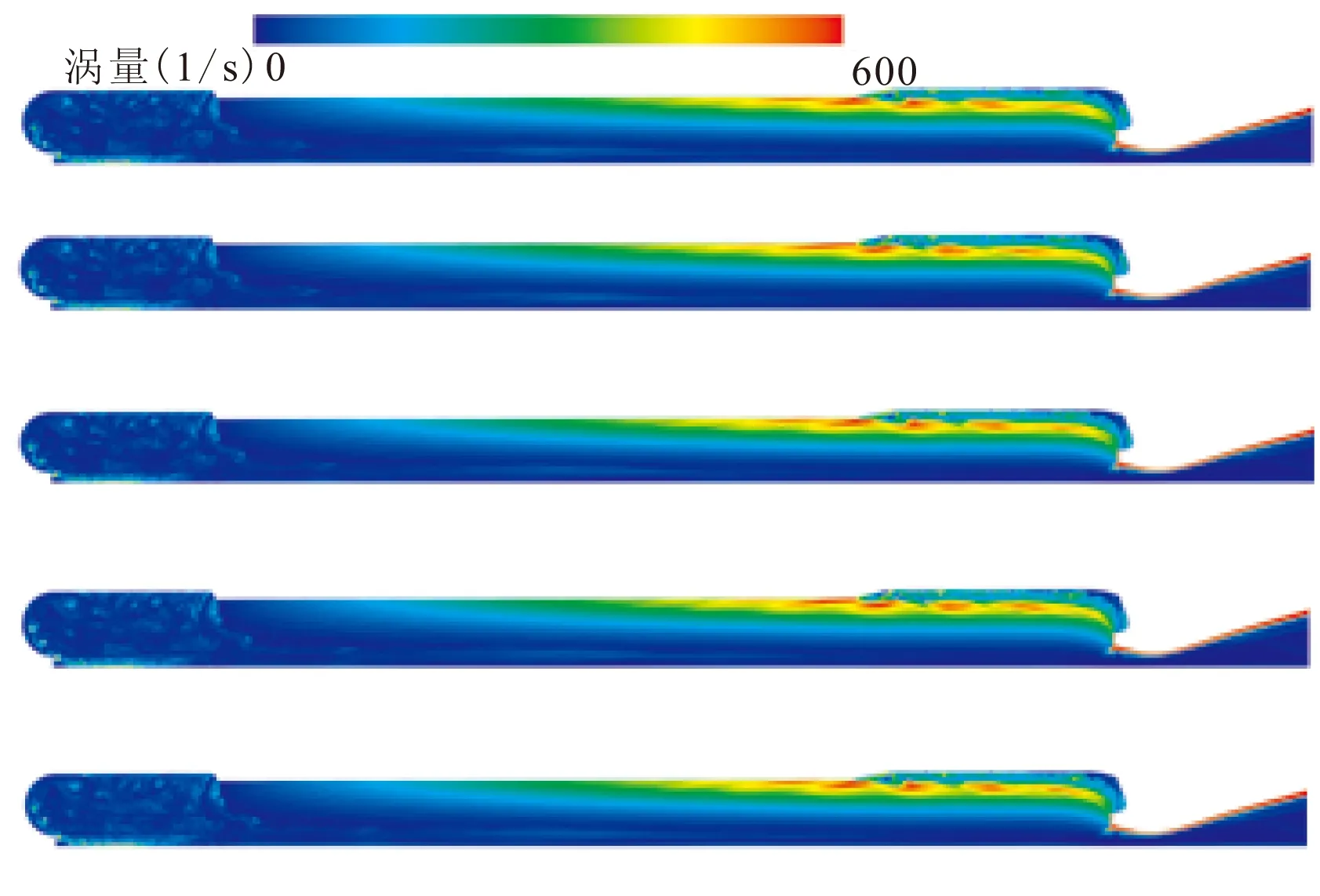
图13　改变装药结构发动机内瞬时涡量云图(时间间隔为0.008 s)

3　结论

(1)针对某固体火箭发动机工作过程中内流场出现的旋涡流动现象，本文通过对发动机工作末期进行大涡模拟，得到了发动机后半段由于装药构型产生的旋涡脱落现象，并得到了由于旋涡脱落产生的发动机内流场压力振荡频率。从压力与速度的脉动幅度来看，沿发动机轴线方向脉动幅度逐渐增加。在相同的轴线位置，靠近发动机头部部分，轴线与壁面处的脉动幅度相当，但在靠近喷管的发动机尾部，壁面处的脉动幅度要大于轴线处的脉动幅度。

(2)在轴向过载条件下，过载条件使得发动机头部压力发生阶跃性下降，而对于受旋涡脱落影响较大的发动机尾部附近，过载条件使得压力产生较强脉冲式振荡，振荡的强度随加载强度的增加而增大，同时过载条件使得发动机尾部压力振荡频率有小幅度增长。

(3)发动机轴向过载时，能引起非常明显的压力脉动，本文的计算中，没有考虑燃烧、过载时结构振动等耦合因素，在过载一定时间后，过载所引起的压力振荡、速度振荡影响逐渐消失。此时，处于过载情况的流动与无过载情况差别较小。最后，通过改变发动机头部装药结构，使得发动机尾部靠近壁面处的旋涡限度大幅减小。

[1]Blomshield F S.Historical perspective of combustion instability in motors-case studies[C]//37th Joint Propulsion Conference and Exhibit，AIAA 2001-3875，Salt Lake City，USA，2001.

[2]Ribéreau D，Pevergne T，Le Helley Ph，et al.Thrust oscillations passive control on large solid rocket motors[C]//41st Joint Propulsion Conference and Exhibit，AIAA 2005-4168，Tucson，Arizona，USA，2005.

[3]Dotson K W，Koshingoe S，Pace K K.Vortex shedding in a large solid rocket motor without inhibitors at the segment interfaces[J].Journal of Propulsion and Power，1997，13(2)：197-206.

[4]Flandro G A，Jacobs H.Vortex generated sound in cavities[R].AIAA 73-1014.

[5]Kourta A.Computation of vortex shedding in solid rocket motors using time-dependent turbulence model[J].Journal of Propulsion and Power，1999，15(3)：390-400.

[6]Luppoglazoff N，Vuillot F.Parietal vortex shedding as a cause of instability for long solid propellant motors-numerical simulation and comparison with firing tests[R].AIAA 96-0761.

[7]Avalon G.Etude experimentale des instabilités naturelles d'un écoulement avec injection a la paroi[R].Campagne d'Essais VECLA ASSM7，Rapport Technique No.4/6163 DSNA/Y/DEFA，March 1999.

[8]Kourta A.Accoustic-mean flow interaction and vortex shedding in solid rocket motors[J].International Journal for Numerical Methods in Fluids，1996，22(6)：449-465.

[9]Lupoglazoff N，Vuillot F.Numerical simulation of vortex shedding phenomenon in 2D test case solid rocket motors[R].AIAA 92-0766.

[10]张翔宇，何国强，刘佩进.固体火箭发动机转角涡脱落分类[J].航空动力学报，2014，29(8)：2003-2011.

[11]张峤，李军伟，王伟臣，等.固体火箭发动机涡声耦合特征数值研究[J].推进技术，2011，32(3)：348-354.

[12]许团委，田维平，王建儒，等.固体发动机地面过载试验凝相粒子加速度分析[J].固体火箭技术，2014，37(4)：486-489.

(编辑：崔贤彬)

Internal flow in a solid rocket motor at the end of burning with axial acceleration

ZHANG Wei-ping1, YANG Dan2, XIONG Yong-liang3

(1.The 41st Institute of the Sixth Academy of China Aerospace Science & Industry Corporation,Huhhot010010,China;2.School of Naval Architecture and Ocean Engineering,Huazhong University of Science & Technology,Wuhan430074,China;3.School of Civil Engineering and Mechanics,Huazhong University of Science & Technology,Wuhan430074,China)

The pressure oscillation observed at the end of burning of solid rocket motor was studied numberically.The large eddy simulation (LES) was adopted to calculate the internal flow of solid rocket motor before it burns out.The angle vortex shedding was obtained due to the angular configuration of the propellant.By monitoring the flow parameters at different positons inside the motor,the frequency of the pressure oscillation due to the vortex shedding was captured.An acceleration condition at the axis direction was introduced to investigate its effect on the pressure oscillation.The results indicate that a pressure pulse was excited and the pressure changes are distinct at different position inside the motor due to the acceleration.The vortex shedding frequency increases slightly due to the overload condition.An improved propellant structure was adopted at the front of the motor and the results show that the vorticity in the end part of the chamber reduces significantly.

solid rocket motor;combustion instability;pressure oscillation;acceleration

2015-05-30；

2015-08-28。

国家自然科学基金(11372079，11502086，11502087)；中央高校基本科研业务费专项资金(2015QN018， 2015QN141)。

张卫平(1973—)，男，高级工程师，研究方向为发动机工作过程仿真。E-mail：yjy0372@sina.com

V435

A

1006-2793(2016)03-0306-06

10.7673/j.issn.1006-2793.2016.03.002