条纹投影三维形貌测量的变分模态分解相位提取
朱新军, 邓耀辉,唐 晨,宋丽梅, 郭庆华
(1.天津工业大学 电气工程与自动化学院,天津 300387;2.天津大学 电子信息工程学院,天津 300072)
条纹投影三维形貌测量的变分模态分解相位提取
朱新军1*, 邓耀辉1,唐晨2,宋丽梅1, 郭庆华1
(1.天津工业大学 电气工程与自动化学院,天津 300387;2.天津大学 电子信息工程学院,天津 300072)
针对条纹投影三维形貌测量涉及的相位提取,提出了一种基于变分模态分解的单幅条纹投影相位提取方法。通过建立变分模态分解模型和极小化变分模态分解将单幅投影条纹图分解成背景部分、条纹部分和噪声部分。然后对得到条纹部分进行Hilbert变换和反正切变换得到包裹相位;对其进行质量导向相位解包裹和Zernike多项式去载频得到解包裹相位。将该方法与Fourier变换、连续小波变换进行了对比,结果显示:本文提出的相位提取方法相位误差为3.14×10-4,小于Fourier变换和连续小波变换方法对应的误差3.30×10-4和6.52×10-4。模拟和实验结果表明:本文提出的方法在处理具有边缘信息投影条纹图时具有优势,能够提取出更准确的相位信息,可有效地用于含边缘不连续和突起的三维物体测量。
条纹投影;三维形貌测量;变分模态分解;相位提取
1 引 言
作为现代光学测试方法中的一种常用方法,条纹投影三维测量具有较高的速度和较高的精度,并且其光学和数字硬件设备比较低廉,近年来已逐渐成为十分受欢迎的一种非接触、快速和高精度的三维形貌测量方法[1-4]。而相位提取是条纹投影的难点,也是重点研究内容,因此,国内外学者提出了多种相位提取方法。总的来讲,条纹投影相位提取方法可分为两类[5-12]:一类是基于单幅条纹图的相位提取,一类是以相移法为代表的基于多幅条纹图的相位提取。由于多幅投影条纹图比单幅投影条纹图提供了更多的信息,通常相移法比其它方法具有更高的精度。与相移法相比,基于单幅投影图的条纹相位提取是在某一时刻只采集一幅图像,受环境扰动的影响较小,更适合动态过程的三维测量和显示。
单幅投影条纹相位提取方法包括Fourier变换(FTM)、连续小波变换(CWT)以及经验模态分解方法[8,10-11]等。这些算法在对噪声的鲁棒性、图像边缘细节的保持等方面进行了改进,但仍然存在缺点。目前为止,经验模态分解处理噪声条纹图时,在分解层数的选择,包络面的选择上存在困难。受噪声的影响,经验模态分解在模态混合问题,严重影响条纹投影条纹分析结果,一般情况下需要进行滤波预处理[8]。此外,经验模态分解需要包络面插值,而包络面插值的计算量巨大。
本课题组前期提出了基于变分图像分解的FPP相位提取方法,其通过变分图像分解,可有效地将条纹图分解为背景部分、条纹部分和噪声部分[13,14]。与Fourier变换,连续小波变换以及经验模态分解方法相比,此方法得到的相位更准确,但此方法的缺点是计算复杂。考虑到变分图像分解和经验模态分解的优势,本文在前期工作的基础上,引入了变分模态分解方法。变分模态分解是一种新的信号分解方法,由Dragomiretskiy和Zosso于2014年提出[15]。变分模态分解能自适应地将几种具有不同模态的信号进行分离。与经验模态分解相比,变分模态分解方法是非递归的,并且具有良好的数学基础。本文提出了基于变分模态分解(Variational Mode Decomposition,VMD)的相位提取方法,将条纹分解成背景部分、条纹部分和噪声部分,再对条纹部分进行包裹相位提取、相位解包裹和去载频,得到最终相位,在文章最后通过模拟和实验验证了提出方法的有效性。
2 基于变分模态分解的条纹相位提取
2.1变分模态分解
变分模态分解是一种新提出的自适应信号分析方法,其建立在变分法和维纳滤波基础上,能自适应地将几种具有不同模态的信号进行分离,即能得到带限本征模态函数。首先,对于每一个本征模态uk,通过Hilbert变换计算得到相应的解析信号,并获得单边频谱。其次,对于每一个单边谱模态,通过混合一个中心频率为wk的指数调制项将每一个频谱移动至“基带”。最后,通过解调信号的H1高斯光滑性(梯度的L2范数)估计带宽。综上所述,对于一维信号f,通过分析变分模态分解构成如下约束变分问题:

(1)
对于二维解析信号uk,其频域可定义为:
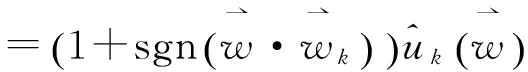
(2)
借助于二维解析信号的定义,二维变分模态分解的能量泛函为:

(3)

采用乘子交替方向法极小化问题[15]。首先,求解关于uk的极小化问题:
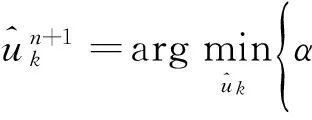

(4)
其中α为正则化参数。
式(4)写成以下维纳滤波结果:
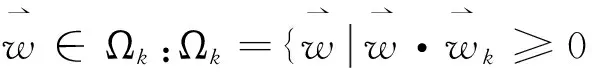
(5)
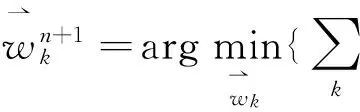
(6)
在频域内:
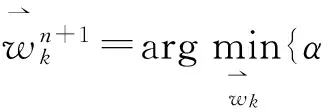

(7)
其解为:

(8)
经过若干次迭代,可实现能量泛函(3)极小化并得到各个模态成分。
2.2基于变分模态分解相位提取
通过极小化能量泛函(3)得到本征模态函数uk,从而有:
(9)
对条纹u2(x,y)进行Hilbert变换得到c(x,y),通过如下反正切函数获得包裹相位图:
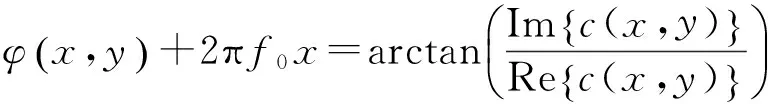
(10)
其中Re{ }与Im{ }分别代表实部与虚部。
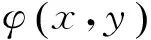
采用Zernike多项式[17]拟合消除载频,将展开后的连续相位表示为n项(Zernike)多项式的组合。记φc(x,y)=2πf0x,写成Zernike多项式的线性组合形式为:
φc(x,y)=a0u0(x,y)+a1u1(x,y)+…+
aiui(x,y)+…+an-1un-1(x,y).
(11)
其中:aiui(x,y)表示第i+1项Zernike多项式,ai表示第i+1项Zernike多项式的系数。在参考面区域内,有:
ψ(x′,y′)=a0u0(x′,y′)+a1u1(x′,y′)+…+
aiui(x′,y′)+…+an-1un-1(x′,y′),
(12)
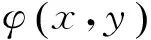
图1总结了上述基于变分模态分解的相位提取的整个过程,主要包含上述的变分模态分解得到条纹、反正切得到包裹相位、解包裹和拟合载频、去除载频5个主要步骤。
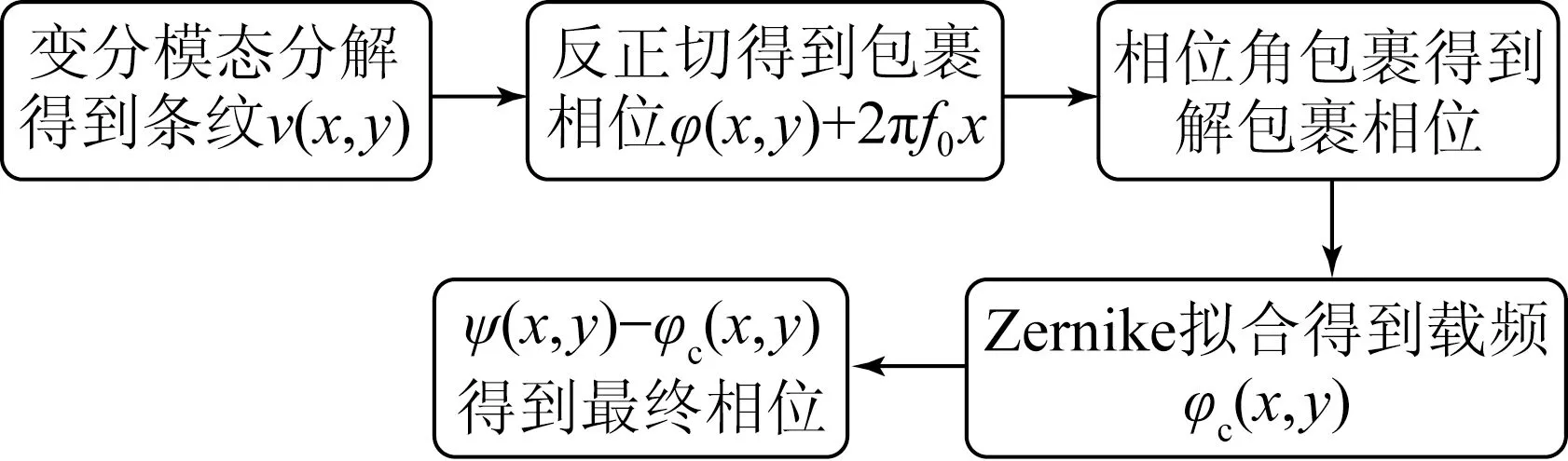
图1 变分模态分解相位提取流程
3 实验结果与分析
3.1仿真模拟
首先采用模拟数据进行分析,模拟的变形条纹图公式为:

n.
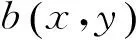
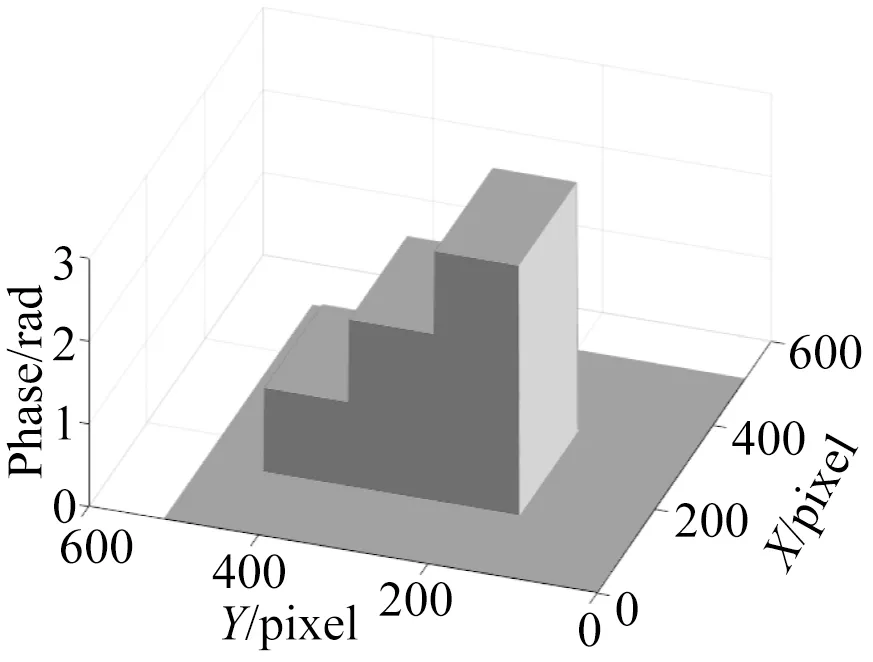
(a)模拟相位(a)Simulated phase(b)模拟投影条纹(b)Simulated projection fringe

(14)
式中M和N为相位的大小。
模拟图结果如图3(彩图见期刊电子版)所示,其中图3(a)、(c)和(e)分别为Fourier变换、连续小波变换与VMD提取的相位结果,图3(b)、(d)和(f)为3种方法第256行数据的结果。利用式(14),可计算出Fourier变换、CWT与VMD处理所得相位误差MSE分别为3.30×10-4和 6.52×10-4和3.14×10-4。从图3和MSE可看出,本文算法给出的相位差更小、结果更准确。
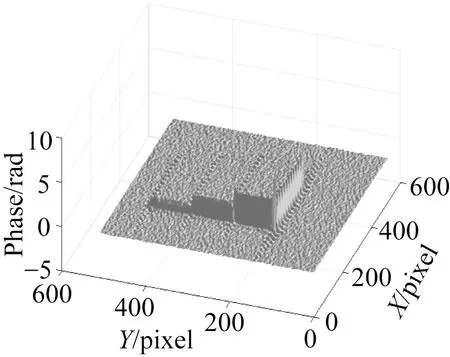
(a)Fourier变换(a)Fourier transfrom (b)图(a)的256行(b)The 256th row of (a)
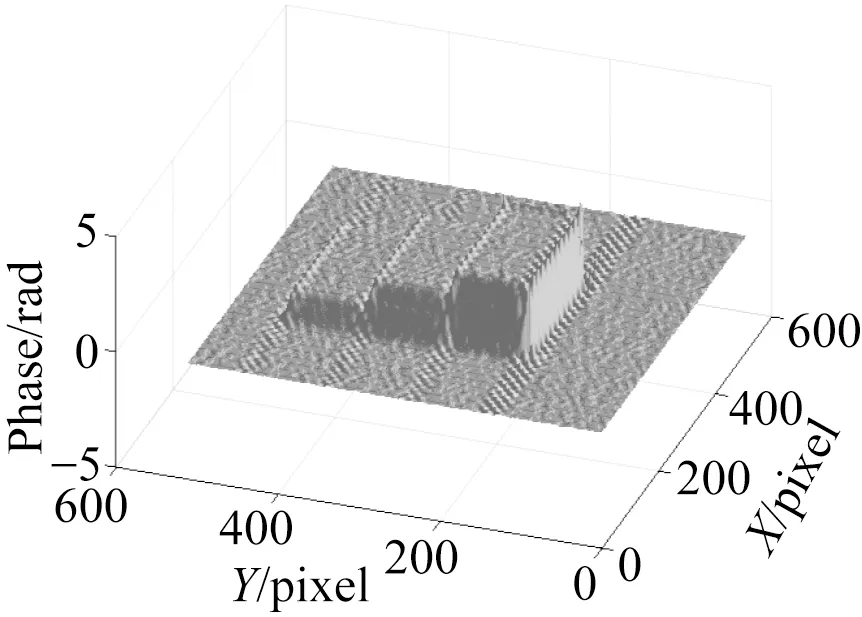
(c)连续小波变换(c) CWT(d)图(c)的256行(d)The 256th row of (c)

(e)变分模态分解(e)VMD(f)图(e)的256行(f)The 256th row of (e)
3.2实验验证
采用两幅实验图像对算法进行测试,图4(a)为石膏人脸模型的投影条纹图,图像大小为512 pixel×512 pixel(西安交通大学械工程学院周翔副教授提供)。图4(b)为实验室采集的人脸模型的条纹图,图像大小同样为512 pixel×512 pixel。图 5(a)、(b)和(c)分别为采用FTM、CWT和VMD方法得到的最终相位图。图5(d)(彩图见期刊电子版)为3种方法与文献[14]中所提VID方法第256列的比较,可以看出,本文方法的结果与文献[14] 所提VID方法的结果最接近,两条线几乎重合。图 6(a)、(b)、(c)和(d)(彩图见期刊电子版)分别为采用四步相移、VMD、FTM、CWT方法得到的最终相位图。从图5可以看出,在石膏人脸的眼部和鼻子等凸起部位,FTM和CWT得到的结果与实际情况差别较大,不能恢复出合理的相位,而采用本文提出的变分模态分解方法则可有效地恢复出合理的相位。从图6可知,本文的VMD得到的相位与四步相移的偏离最小,FTM次之,CWT偏差最大。以上结果表明在处理具有边缘信息的物体投影条纹图时,本文方法更具有优势,能够提取出更准确的相位信息,能够有效进行具有不连续和突起的三维物体测量。

(a)石膏人脸(a)Plaster face (b)面具模型(b)Mask model

(a)Fourier 变换(a)Fourier transform(b)连续小波变换(b)CWT
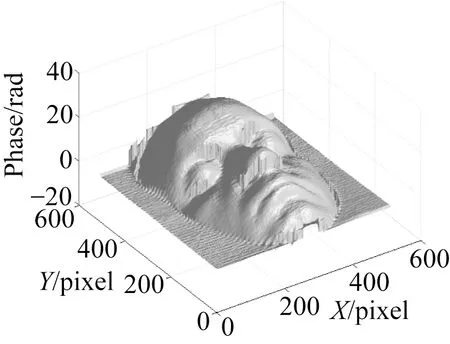
(c)本文方法(c) Proposed method(d)图(a),(b),(c)第256列相位值(d)Phase value of 256th column in (a),(b),(c)
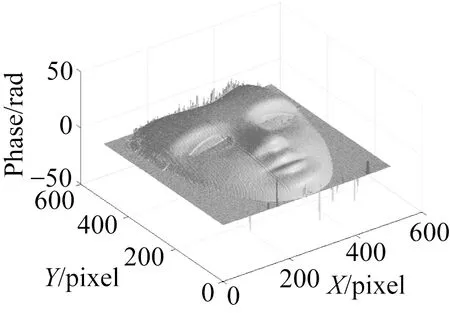
(a)四步相移(a)Four steps phase shift (b)本文方法(b)Proposed Method

(c)Fourier 变换(c)FTM(d)连续小波变换 (d)CWT

(e)图(a),(b),(c)和(d)第256行结果(e)Results of the 256th row in (a),(b),(c) and (d)
3.3动态实验
本节采用实验室搭建的条纹投影测量系统对人脸表情的动态三维形貌进行测量,并用VMD方法对测量数据进行相位提取。实验系统主要包括数字投影仪(德州仪器公司 DLP LightCrafter 3000),高速CCD摄像机(奥林巴斯 i-SPEED TR)。DLP投影仪将正弦条纹投射到真实人脸,高速摄像机以20 frame/s的速度采集变形投影条纹图。图7(a)和(b)为两幅不同时刻得到的人脸变形条纹图,图7(c)和(d)为相位提取结果,由图7可知,本文方法能较好地反应人脸的鼻子、眼部和嘴部的细节信息。

(a)投影条纹图1(a)Projection fringe 1 (b)投影条纹图2 (b)Projection fringe 2

(c)图(a)处理结果(c)Result of Fig.7 (a)(d)图(b)处理结果 (d)Result of Fig.7 (b)
综上所述,本文提出的方法在更大程度上保持了条纹在物体表面边缘不连续处和剧烈突起处的细节。因此,本文提出的方法可更有效地用于边缘和剧烈突起的物体表面三维形貌测量中。
4 结 论
本文首先提出了一种基于变分模态分解的条纹投影相位提取方法,该方法可以有效地将FPP条纹图分解成背景部分、条纹部分和噪声部分,再对条纹部分进行相位提取,从而得到最终的相位。在分解条纹图的过程中,首先通过分析变分模态分解模型,给出了变分图像的分解模型与优化方法,从而得到条纹部分。然后,经过反正切得到包裹相位,通过相位解包裹得到解包裹相位,通过Zernike拟合载频,去除载频后得到最终的相位。通过模拟实验可知,本文提出的相位提取方法的相位误差为3.14e×10-4,优于FTM、CWT的3.30×10-4和6.52×10-4。模拟和实验结果表明该方法在相位提取方面能更好地保持相位边缘信息,更有效地用于具有边缘和剧烈突起的物体表面三维形貌测量中。
[1]GORTHI S S, RASTOGI P. Fringe projection techniques:Whither we are? [J].Opt.LasersEng., 2010, 48 (2): 133-140.
[2]DAI M L, YANG F J, HE X Y. Single-shot color fringe projection for three-dimensional shape measurement of objects with discontinuities [J].Appl.Opt., 2012, 51(12): 2062-2069.
[3]张鹏,张元,金光,等. 应用条纹投影法测量薄膜反射镜的成形[J]. 光学 精密工程,2011, 19(6): 1185-1191
ZHANG P, ZHANG Y, JIN G,etal.. Measurement of space membrane mirror shaping based on fringe projection [J].Opt.PrecisionEng., 2011, 19(6): 1185-1191. (in Chinese)
[4]安东,陈李,丁一飞, 等.光栅投影相位法系统模型及标定方法[J].中国光学, 2015,8(2): 248-254
AN D, CHEN L, DING Y F,etal.. Optical system model and calibration of grating projection phase method [J].ChineseOptics, 2015, 8(2): 248-254. (in Chinese)
[5]张旭,李祥,屠大维. 相位高度的显函数模型及其标定[J]. 光学 精密工程, 2015, 23(8): 2384-2392
ZHANG X,LI X,TU D W. Explicit phase height model and its calibration [J].Opt.PrecisionEng., 2015, 23(8): 2384-2392. (in Chinese)
[6]戴美玲,杨福俊,何小元. 基于双频彩色光栅投影测量不连续物体三维形貌[J]. 光学 精密工程, 2013, 21(1): 7-12
DAI M L,YANG F J,HE X Y. Three-dimensional shape measurement of objects with discontinuities by dual-frequency color fringe projection [J].Opt.PrecisionEng., 2013, 21(1): 7-12. (in Chinese)
[7]武迎春,曹益平,肖焱山. 任意相移最小二乘法迭代的在线三维检测[J]. 光学 精密工程, 2014, 22(5): 1347-1353WU Y CH,CAO Y P,XIAO Y SH. On-line three-dimensional inspection using randomly phase-shifting fringe based on least-square iteration [J].Opt.PrecisionEng., 2014, 22(5): 1347-1353. (in Chinese)
[8]ZHOU X, PODOLEANU A, YANG Z Q,etal.. Morphological operation-based bi-dimensional empirical mode decomposition for automatic background removal of fringe patterns[J].Opt.Express, 2012,20(22): 24247-24262.
[9]GUTIÉRREZ-GARCA J C, MOSIO J F, MARTNEZ A,etal.. Practical eight-frame algorithms for fringe projection profilometry [J].Opt.Express, 2013, 21(1): 903-917.
[10]TAKEDA M, MUTOH K. Fourier transform profilometry for the automatic measurement of 3-D object shapes [J].ApplOpt,1983, 22(24): 3977-3982.
[11]MA J, WANG Z, VO M, PAN B. Wavelet selection in two-dimensional continuous wavelet transform technique for optical fringe pattern analysis[J].JournalofOptical, 2012,14(6): 065403.
[12]ZHENG S, CAO Y. Fringe-projection profilometry based on two-dimensional empirical mode decomposition [J].Appl.Opt., 2013, 52(31): 7648-7653.
[13]ZHU X, CHEN Z, TANG C. Variational image decomposition for automatic background and noise removal of fringe patterns [J].Opt.Lett., 2013, 38 (3): 275-277.
[14]ZHU X J, TANG C CH, LI B,etal.. Phase retrieval from single frame projection fringe pattern with variational image decomposition [J].Opt.LasersEng., 2014,59:25-33.
[15]DRAGOMIRETSKIY K, ZOSSO D. Variational mode decomposition [J].IEEETransactionsonSignalProcessing, 2014, 62(3):531-544.
[16]GHIGLIA D C, PRITT M D.Two-dimensionalPhaseUnwrapping:Theory,Algorithm,andSoftware[M]. New York: Wiley, 1998.
[17]ZHANG Q, WU Z. A carrier removal method in Fourier transform profilometry with Zernike polynomials [J].Opt.LasersEng., 2013, 51(3): 253-260.

朱新军(1985-),男,山东临沂人,博士,讲师,2008年于临沂大学获得学士学位,2011年于山东理工大学获得硕士学位,2015年于天津大学获得博士学位,现为天津工业大学电气工程与自动化学院讲师,主要从事光干涉测量、散斑测量及机器视觉的研究。E-mail: xinjunzhu@tjpu.edu.cn

邓耀辉(1993-),男,河北石家庄人,硕士研究生,2015年于河北工业大学获得学士学位,主要从事三维重建、机器视觉、模式识别等领域的研究。E-mail: 18202511970@163.com
(版权所有未经许可不得转载)
Variational mode decomposition for phase retrieval in fringe projection 3D shape measurement
ZHU Xin-jun1*, DENG Yao-hui1, TANG Chen2, Song Li-mei1, GUO Qing-hua1
(1.SchoolofElectricalEngineeringandAutomation,TianjinPolytechnicUniversity,Tianjin300387,China;2.SchoolofElectronicInformationEngineering,TianjinUniversity,Tianjin300072,China)*Correspondingauthor,E-mail:xinjunzhu@tjpu.edu.cn
For the phase retrieval in fringe projection 3D shape measurements, a new fringe projection phase retrieval method based on variational mode decomposition was proposed. Firstly, the projection fringe pattern was decomposed into a background part, a fringe part and a noise part by the development of variational mode decomposition model and the minimization of the model. Then, the fringe part was processed by Hilbert and arc tangent transform to obtain a wrapping phase, and by quality guided phase unwrapping and Zernike carrier removal to acquire the final absolute phase. Simulation and experimental results show that the phase error by the proposed method is 3.14×10-4,smaller than the errors 3.30×10-4and 6.52×10-4that respectively obtained by Fourier transform method and continuous wavelet transform method. The proposed method is superior to the Fourier transform method and continuous wavelet transform method in the process of projection fringes with edge information, providing more accurate results, and is more effective for the application of the three dimensional measurement of objects with discontinuous and abrupt changes.
fringe projection; three dimensional measurement; variational mode decomposition; phase retrieval
2016-06-05;
2016-08-01.
国家自然科学基金资助项目(No.60808020,No.61078041);天津市应用基础与前沿技术研究计划资助项目(No.15JCYBJC51700)
1004-924X(2016)09-2318-07
TP92;O436.1
A
10.3788/OPE.20162409.2318

