压电微位移台的动态迟滞建模及实验验证

杨晓京，彭芸浩，李　尧

(昆明理工大学 机电工程学院，云南 昆明 650500)



压电微位移台的动态迟滞建模及实验验证

杨晓京*，彭芸浩，李尧

(昆明理工大学 机电工程学院，云南 昆明 650500)

为了提高压电微位移平台快速定位的精确度，建立了一种表征压电微位移平台驱动电压与输出位移关系的定位模型。考虑压电工作台在快速、大行程精确定位过程中会受压电陶瓷迟滞特性及本身动态特性的影响，本文采用Bouc-Wen模型描述压电陶瓷迟滞特性，并结合压电工作台的动态特性进行共同建模，使模型同时体现压电工作台的动态特性与迟滞特性。为了验证模型的正确性，搭建了基于压电微位移平台和相关驱动器的实验设备对模型进行了实验验证，并进行了测控程序的二次开发。研究结果表明，与单纯的Bouc-Wen模型相比，提出模型在最大位移输出为40 μm，输入电压频率为40 Hz时的最大误差由3.04 μm下降到了0.67 μm，此时最大相对误差为1.68%。得到的结果验证了提出的模型可较好地模拟压电工作台的迟滞特性与动态特性，大大提高压电微位移平台在快速、大行程定位中的精确度。

压电微位移台；动态特性；迟滞特性；Bouc-Wen模型；运动定位

1　引　言

压电微位移平台是基于柔性铰链机构，由压电陶瓷提供驱动力的微位移精密机构。具有分辨率高、无摩擦、响应快和无噪音等优点，被广泛应用于超精密加工制造、微纳定位、生物工程、微机电系统等领域[1]。但是，压电陶瓷驱动器的输入电压与输出位移之间存在的迟滞非线性，压电陶瓷驱动器本身具有的蠕变性以及压电工作台的动态特性，都会对压电工作台的定位准确度造成影响，使其定位精度降低[2]。

为了提高微位移平台的定位精度，国内外很多专家学者提出了不同的压电驱动器设计方案[3-5]，同时也对压电陶瓷微位移器的数学模型进行了大量的研究，建立了Preisach模型[6-7]、Prandtle-Ishlinskii模型[8-9]、Duhem模型[10-11]、Bouc-Wen模型[12-14]等迟滞模型。但是，这些模型均不能表示微位移平台运动过程的全部信息，大部分模型仅能表示压电执行器的迟滞性、蠕变性或平台的动态特性。由于压电驱动器的蠕变性在平台的慢速定位中影响显著，迟滞性在大行程定位中显示明显，而平台快速运动中主要体现动态特性[2]，这就使得在进行大行程、快速定位的时候，微位移平台的定位精度不高。为了提高平台的定位精度，就必须将压电微位移平台的动态特性和迟滞特性结合起来建模。

本文选取Bouc-Wen模型对平台的迟滞特性进行数学建模。Bouc-Wen模型是由Bouc[15]于1967年提出，并由Wen[16]于1976年完善的微分方程。该方程由一系列不定参数构成，不同的参数对应于不同的迟滞环。近年来，众多学者对该模型模拟压电陶瓷的迟滞性进行了研究[12-14]，取得了一定成果。同时，该模型本身为动态模型，与静态模型相比，能较好的反应压电执行器的动态迟滞性，但随着输入信号频率的上升，模型的准确性会逐步下降。为了进一步提高平台在大行程、较快速度下的定位精度，本文研究了压电工作台的线性动态模型，并通过将线性动态模型与迟滞模型相结合，得到了更加精确的动态迟滞模型，使得该模型能够同时表示压电微位移平台的动态特性和迟滞特性。最后，以三维压电微位移平台为对象，验证了由线性动态模型与迟滞模型结合的动态迟滞模型的精确性，并将其与单纯基于Bouc-Wen模型建模的结果进行了比较，验证了模型的优越性。

2　动态迟滞模型

2.1动态迟滞模型的建立过程

压电微位移平台主要由压电驱动器和柔性铰链等组成，其特性主要由压电驱动器的迟滞性、蠕变性，位移平台的动态特性来表现。因此，微位移平台系统为典型的二阶系统[17]。当压电工作台的工作频率远小于其谐振频率时，可将工作台系统看做一个弹簧-阻尼系统。其中，弹簧表示压电驱动器的特性，阻尼表示柔性铰链的特性。则系统的力与位移的关系为：

(1)

同时，工作台的输出力还与压电驱动器的输出力呈迟滞非线性关系：

F(t)=H{V(t)}.

(2)

联立式(1)、(2)，转换成标准的二阶系统的形式：

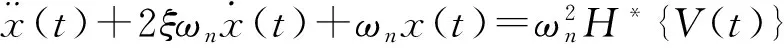
(3)

式(3)即为压电微位移平台的动态迟滞模型，既体现出了微位移平台的迟滞特性，又表示出了平台的动态特性。

2.2Bouc-Wen模型的建立过程

图1所示为压电微位移平台的迟滞曲线。图中虚线所示为迟滞曲线上位移最大值与最小值的连线。压电微位移平台的迟滞曲线即可看成是该直线加上曲线的迟滞分量构成的：

x(t)=kvu(t)+h(t)+x0，

(4)

式中：x(t)为输出位移，u(t)为输入电压，kv为构成输入电压与输出位移线性关系的比例常量，h(t) 为迟滞分量，x0为初始位移。

其中，h(t)的一阶导数为[15]：

，

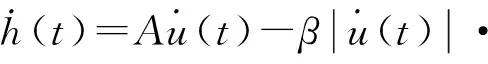
(5)

式中：A、β、γ为待求参数。为了简化辨识过程，降低辨识难度，通常情况下将n设为1，则有：

(6)

则只需要确定参数kv，A、β、γ便能得到相应的Bouc-Wen模型。

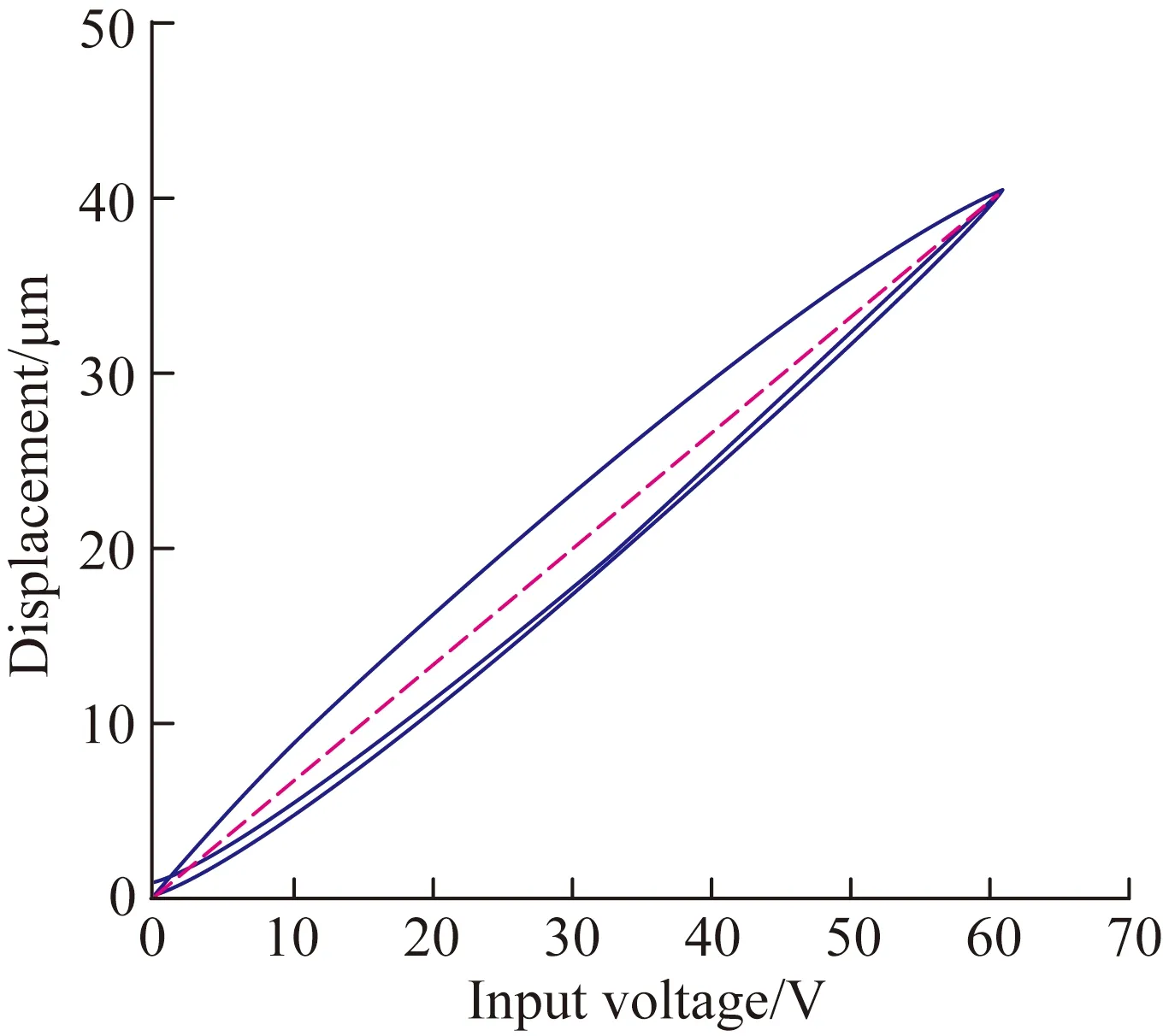
图1压电微位移平台输入电压与输出位移的迟滞曲线

Fig.1Hysteresis curves of input voltage and output displacement of piezoelectric positioning stage

3　模型参数的辨识

压电微位移平台的动态迟滞模型由平台的迟滞特性和动态特性组成，因此，建模也可以分成这两个部分进行。当压电平台进行慢速定位时，平台的动态特性表现不明显，平台主要表现为迟滞特性。则模型方程可简化为：

x(t)=H*{V(t)}.

(7)

此时，仅需要对系统进行迟滞模型的建立即可。Bouc-Wen模型的参数辨识过程如下：

对压电微位移平台输入两组电压u(t)和u′(t)，它们之间的关系为u′(t)=u(t)±c(c为常数)，将其分别代入式(4)，得：

(8)

由式(8)可解得：

(9)

又对于一个完整的迟滞过程来说，h(t)的变化量为0，则有：

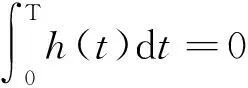
(10)

由式(10)和式(8)，可以确定初始位移x0：

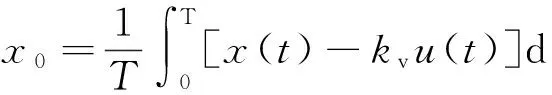
(11)

由式(6)可得：

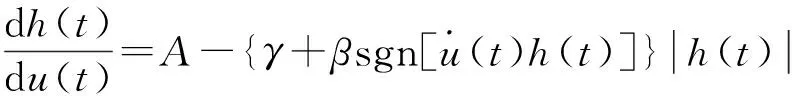
(12)

在图1中求得直线与迟滞曲线的交点(u0，x0)，由Bouc-Wen模型的性质可知，此时h(t)为0。则由式(8)、(12)可得：

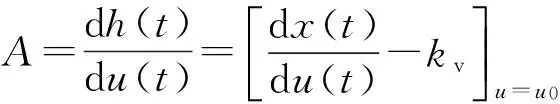
(13)

在上升曲线中，当点(u1，x1)处于(u0，x0)下方时，由式(12)可得：

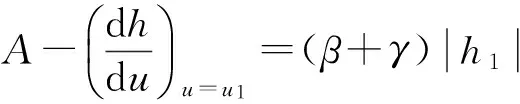
(14)

同样，在上升曲线上取点(u2，x2)处于(u0，x0)上方，同理可得：

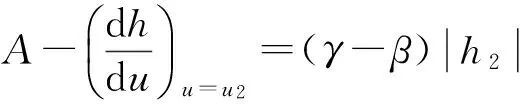
(15)

联立式(14)、(15)可得：

(16)

至此，Bouc-Wen模型的所有参数均求解完成，平台的迟滞模型也建立完成。当压电微位移平台进行小行程快速定位时，平台的迟滞性表现不明显。此时，平台表现线性动态性，则式(3)可写为：

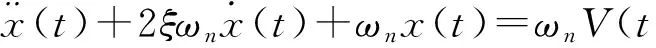
(17)

此时，需要确定的参数为ξ和ωn，可由线性系统的频率响应辨识法获得。

4　实验验证

4.1实验装置

采用如图2所示的实验装置，来完成Bouc-Wen模型和线性动态模型的数据采集和模型的验证实验。该实验装置采用哈尔滨芯明天科技有限公司生产的三维压电微位移平台XP-611.XYZ和XE-500/501 D系列压电陶瓷控制器搭建组成，并进行了测控程序的二次开发。

以X轴方向为例进行实验。压电微位移平台X轴的基本参数如下：输入电压为0～150 V；最大输出位移为120 μm(±20%)；开环定位分辨率为0.2 nm；重复定位精度为30 nm；空载响应频率为350 Hz。XE-500/501 D系列压电陶瓷控制器由放大器模块、传感器控制模块和显示与接口模块等组成。实验过程中，通过压电陶瓷控制器驱动微位移平台，并与计算机相连，采用基于LabVIEW的数据采集处理程序，对数据进行采集处理。

图2　实验装置实物图

4.2Bouc-Wen模型参数辨识

为了得到准确的参数值，先让压电微位移平台输入一组0.2 Hz，电压分别为0～61 V、30～91 V，最大位移分别为40 μm、62 μm的正弦信号，如图3所示。

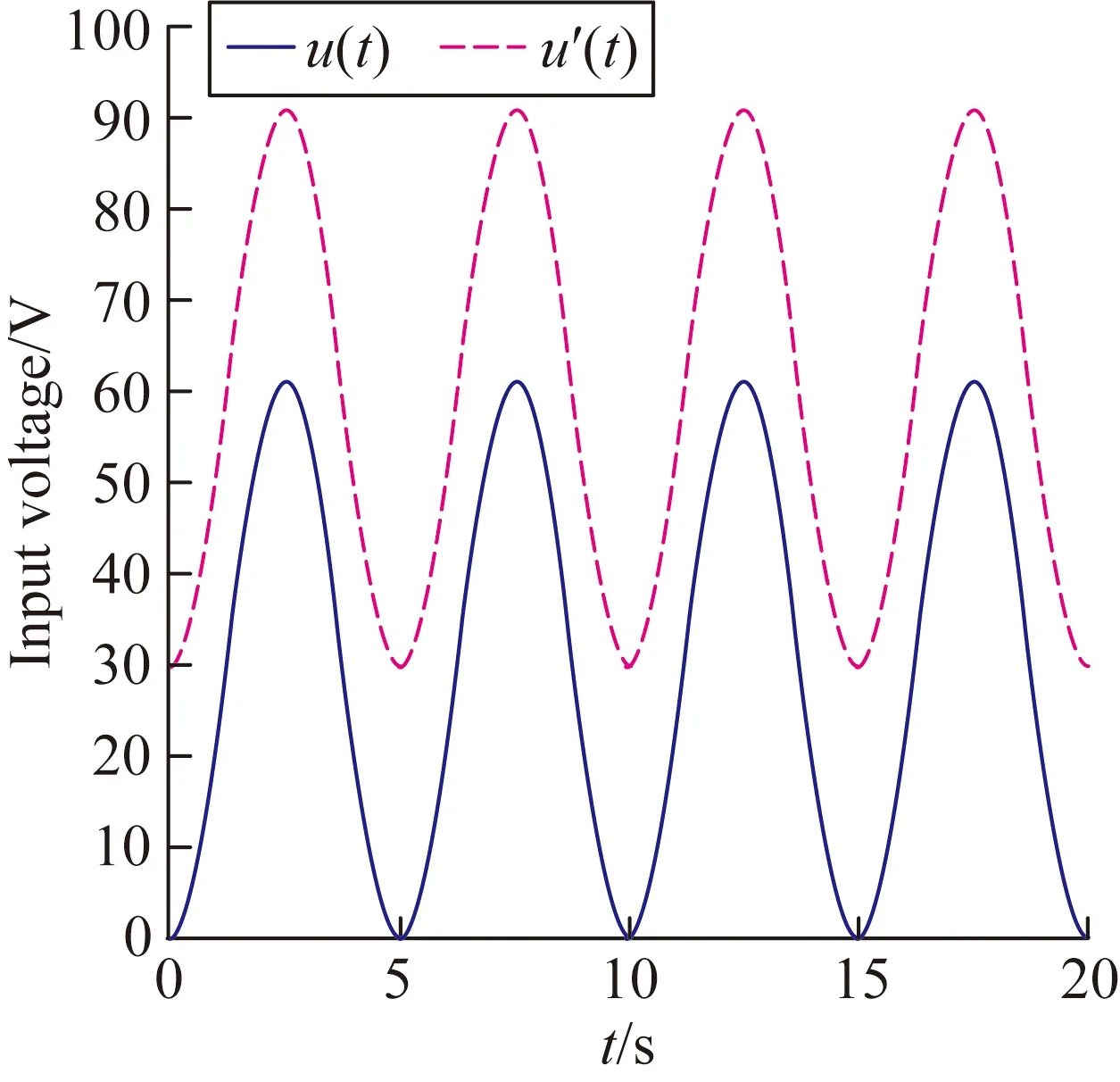
(a)输入电压时间曲线

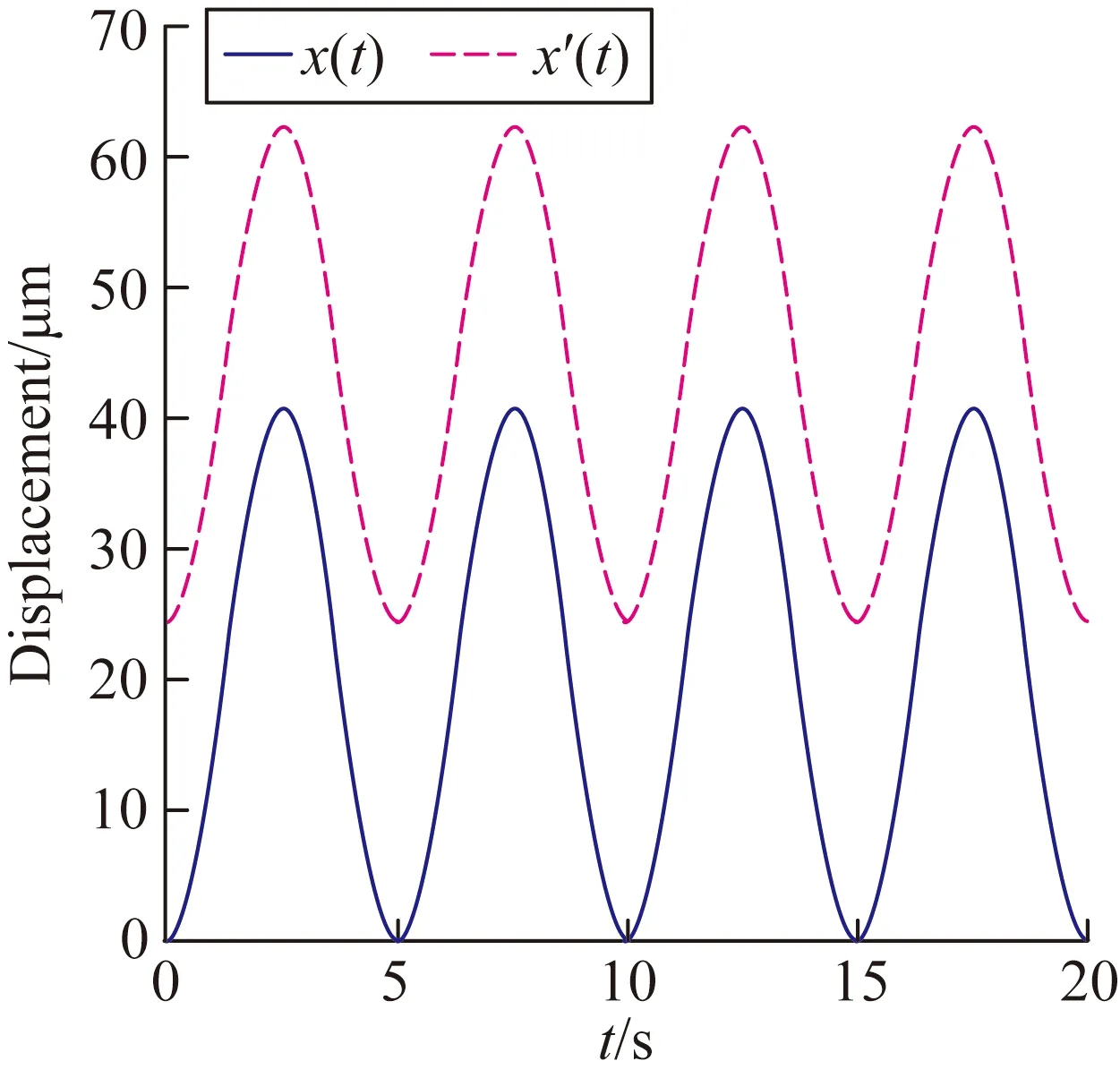
(b)输出位移时间曲线

由图3和式(9)、(11)、(13)、(16)可得模型的参数分别为：kv=7.015×10-7，x0=0.354×10-6，A=-1.87×10-7，β=0.085 4，γ=-0.093 5。

再将各参数代入式(4)、(6)，即可求出Bouc-Wen模型的表达式，完成模型的建立。

4.3动态特性的辨识

平台的动态特性参数由频域响应法获取，由于压电微位移平台X轴向的空载响应频率为350 Hz，所以，将输入电压信号由0 Hz逐步加至550 Hz，平台的最大位移控制在6 μm左右。通过MATLAB以二阶系统传递函数的形式，对实验数据进行处理。得到的动态特性的参数为：

(18)

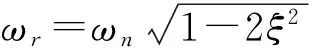
4.4动态迟滞模型的验证

结合迟滞模型和平台的动态特性模型，将两模型代入式(3)中，即可建立平台的动态迟滞模型。为了验证模型的准确性，将平台的输入电压信号设置为40 Hz的正弦信号，最大位移定为40 μm，并与单纯的Bouc-Wen模型建模进行比较，结果如图4所示。

图4　Bouc-Wen模型与实际迟滞环

图4所示为单纯的Bouc-Wen模型与实际迟滞环的电压-位移曲线图。从图中可以看出，在压电微位移平台较快速、大行程定位时，用单纯的Bouc-Wen模型进行压电微位移平台迟滞模型的描述时，出现了较大的误差，模型最大误差出现于最大位移40 μm处，误差为3.04 μm，且模型较实际迟滞环有向下的偏移，这是由于单纯的Bouc-Wen模型没有考虑到平台自身的动态特性，因此在平台快速定位的过程中产生了较大的误差，且随着平台位移的增大，误差也随之增大。图5所示为改进后的动态迟滞模型与实际迟滞环的电压-位移曲线图、误差曲线图和输出位移时间曲线图。由于改进后的动态迟滞模型考虑到了平台本身的动态特性，在单纯的Bouc-Wen模型中加上了平台的动态特性，所以得到了较好的精度，提高了模型的精确度，最大误差为0.67 μm，最大相对误差为1.68%。

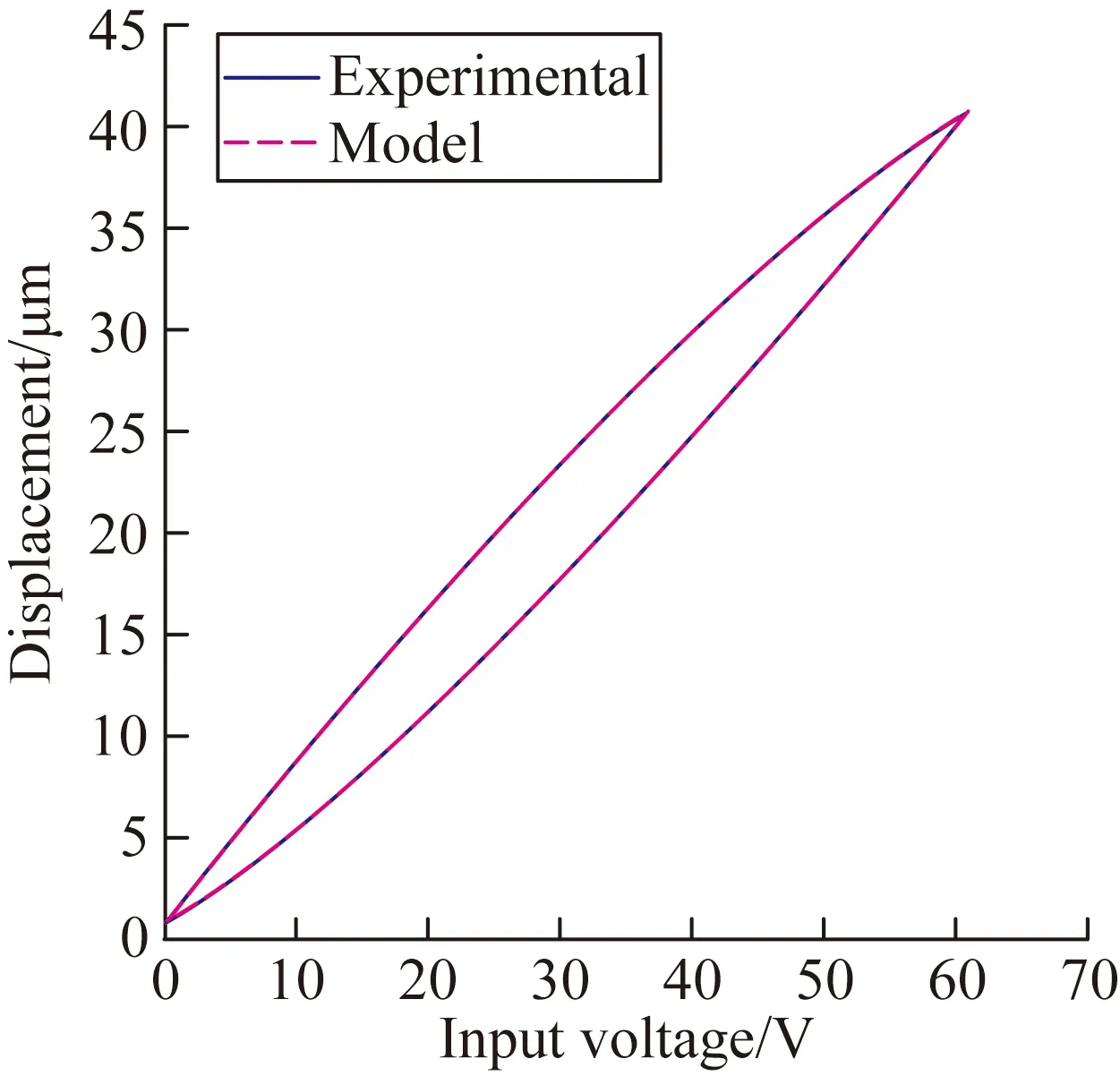
(a)动态模型与实际迟滞环

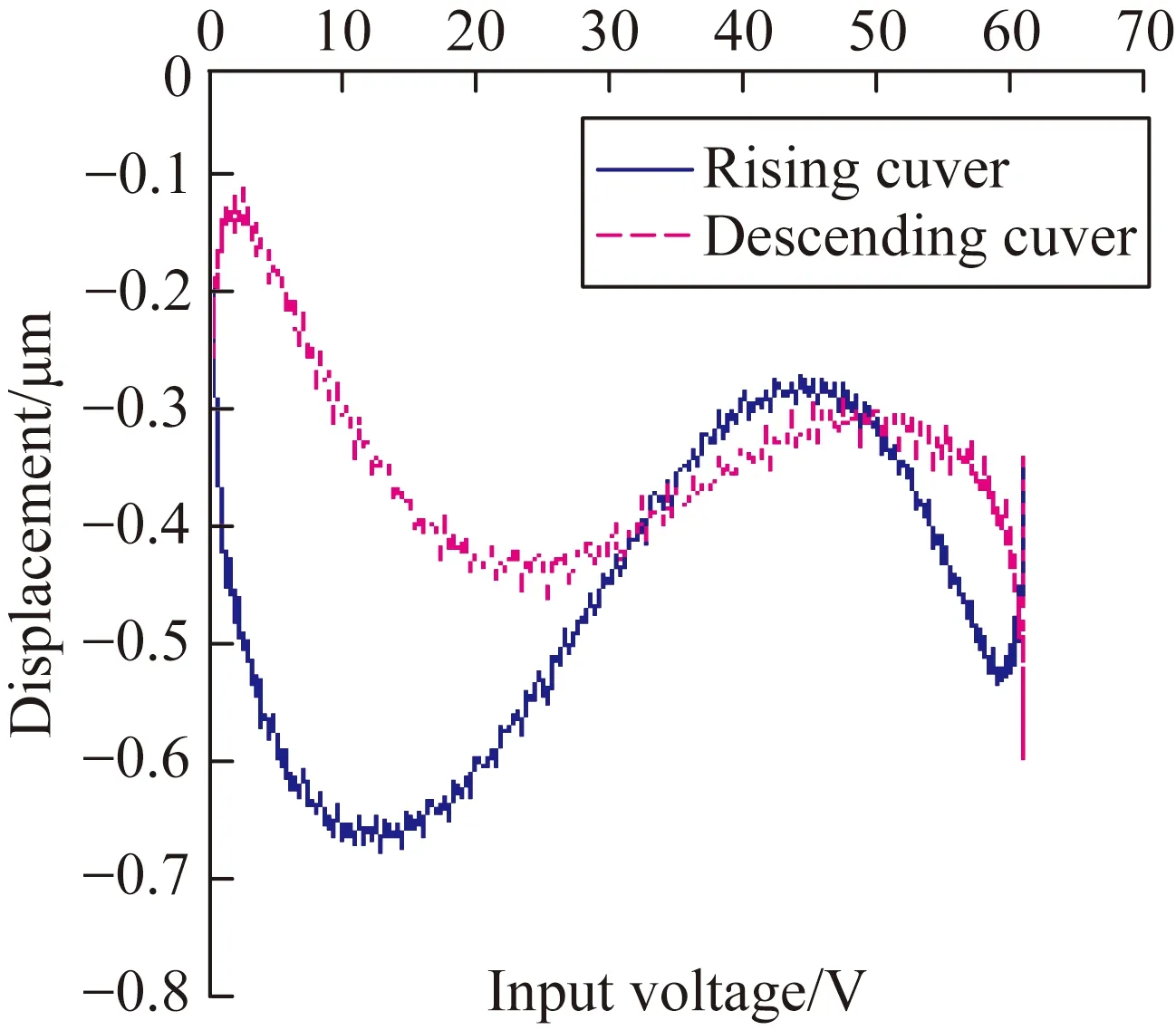
(b)动态模型的位移误差与驱动电压之间的关系曲线

(c)输出位移时间曲线

图5模型预测的压电陶瓷微位移平台的结果与实验测量结果的比较

Fig.5Comparisons between predicted results from piezoelectric micro displacement platform by model and measured results

5　结　论

本文提出了一种表征压电微位移平台输出位移与输入电压之间关系的动态迟滞模型。主要应用于压电微位移平台进行较大行程、快速定位过程中。模型是在Bouc-Wen模型的基础上加上了压电微位移平台的动态特性而建立起来的动态迟滞模型，既能表现出微位移平台在快速定位过程中出现的动态特性，又能体现出平台在大行程定位过程中出现的迟滞特性。实验表明，在最大位移输出为40 μm，输入电压频率为40 Hz时，模型的最大误差由单纯使用Bouc-Wen模型时的3.04 μm 下降到了0.67 μm。此时，模型的最大相对误差为1.68%，验证了该模型能大大提高压电微位移平台在快速、大行程定位中的精确度。需要说明的是，实验验证以国产代表性的哈尔滨芯明天科技有限公司生产的压电微位移平台和驱动器为基础进行的。在实际应用中，根据压电微位移平台类型，仅需在模型的基础上对其主要参数进行识别，即可得到一种能更加精确描述压电微位移台动态迟滞现象的模型，模型具有广泛适用性。为高性能压电微位移平台控制系统的设计提供了参考。

[1]李庆祥，王东生，李玉和.现代精密仪器设计[M]. 北京:清华大学出版社，2004.

LI Q X， WANG D SH， LI Y H.DesignofModernPrecisionInstruments[M]. Beijing:Tsinghua University Press，2004.(in Chinese)

[2]张栋，张承进，魏强.压电微动工作台的动态迟滞模型[J]. 光学 精密工程，2009，17(3):549-556.

ZHANG D， ZHANG CH J， WEI Q. Dynamic hysteresis model of piezopositioning stage[J].Opt.PrecisionEng.，2009，17(3):549-556.(in Chinese)

[3]WANG Z W， LI T J. Optimal Piezoelectric sensor/actuator placement of cable net structures using H_2-norm measures [J].Journalofvibration&control， 2014，20(8):1257-1268.

[4]王志斌，李克武，张瑞，等. 基于铌酸锂制作光弹调制器用压电驱动器[J].光学 精密工程，2015，23 (1):63-69.

WANG ZH B， LI K W， ZHANG R，etal.. Fabrication of piezoelectric actuator for photoelastic modulator based on lithium niobate[J].Opt.PrecisionEng.，2015，23(1):63-69. (in Chinese)

[5]刘泊，郭建英，孙永全.压电陶瓷微位移驱动器建模与控制[J].光学 精密工程，2013，21(6):1503-1509.

LIU B，GUO J Y，SUEN Y Q.Modeling and control for PZT micro-displacement actuator[J].Opt.PrecisionEng. ，2013，21(6):1503-1509. (in Chinese)

[6]LI Z， SU CY， CHAI T. Compensation of hysteresis nonlinearity in magnetostrictive actuators with inverse multiplicative structure for preisach model[J].IEEETransactionsonAutomationScienceandEngineering， 2014，11(11):613-619.

[7]李黎，刘向东，王伟，等.压电陶瓷执行器迟滞特性的广义非线性Preisach模型及其数值实现[J].光学 精密工程，2007，15(5):706-712.

LI L， LIU X D， WANG W，etal.. Generalized nonlinear Preisach model for hysteresis nonlinearity of piezoceramic actuator and its numerical implementation [J].Opt.PrecisionEng. ，2007，15(5):706-712. (in Chinese)

[8]GU G Y， ZHU L M， SU C Y，etal.. Modeling and compensation of asymmetric hysteresis nonlineairty for piezoceramic actuators with a modified prandtl-ishlinskii model[J].IEEETransactionsonIndustrialElectronics， 2013，61(3):1583-1595.

[9]方凡，崔玉国，梁冬泰，等.压电微动平台的改进PI迟滞模型研究[J].压电与声光，2014，36(1):69-75.

FANG F， CUI Y G， LIANG D T，etal..Research on improved hysteresis model of piezoelectric micro positioning stage [J].PiezoelectricandAcoustooptics，2014，36(1):69-75.(in Chinese)

[10]王晓东，江国栋.压电陶瓷迟滞建模及控制仿真[J].压电与声光，2015，37(36):926-929.

WANG X D，JIANG G D.Hysteresis modeling and control simulation of piezoelectric ceramic[J].PiezoelectricandAcoustooptics，2015，37(36):926-929.(in Chinese)

[11]孙孔政.压电陶瓷系统迟滞非线性建模与控制的研究[D].北京:中国科学院，2013.

SUEN K ZH.Researchbasedonpiezoelectricceramicshysteresisnonlinearmodelingandcontrol[D]. Beijing:Graduate University of the Chinese Academy of Sciences，2013. (in Chinese)

[12]XIAO S L， LI Y M. Dynamic compensation andH∞ control for piezoelectric actuators based on the inverse Bouc-Wen model[J].RoboticsandComputer-IntegratedManufacturing， 2014， 30(1):47-54.

[13]袁刚，张小波，王代华，等. 压电式快速控制反射镜的迟滞特性及线性化[J].光学 精密工程，2015，23(6):1650-1656.

YUAN G， ZHANG X B， WANG D H，etal.. Hysteresis and linearization of piezoelectric fast steering mirror[J].Opt.PrecisionEng. ， 2015， 23， (6):1650-1656.(in Chinese)

[14]朱炜，芮筱亭.压电执行器的Bouc-Wen模型在线参数辨识[J].光学 精密工程，2015，23(1):110-116.

ZHU W， RUI X T. Online parameter identification of Bouc-Wen model for piezoelectricactuator[J].Opt.PrecisionEng. ，2015，23(1):110-116.(in Chinese)

[15]BOUC R．Forced vibration of mechanical systems with hysteresis[C].Proceedingsofthe4thConferenceonNonlinearOscillations，Prague，Czechoslovakia， 1967: 315.

[16]WEN Y K. Method for random vibration of hysteretic systems[J].ASCEJournalofEngineeringMchanics， 1976， 102(2): 249-263.

[17]ADRIAENS H， KONING W， BANNING R.Modeling piezoelectric actuators[J].IEEE/ASMETransactionsonMechatronics， 2000， 5(4):331-341.

杨晓京(1971-)，男，云南大理人，教授，博士生导师，1993年、1996年于中国农业大学分别获得学士、硕士学位，2008年于浙江大学获得博士学位，2013年于昆明理工大学博士后出站。主要从事超精密驱动与传动理论及新技术等方面的研究。E-mail:xjyang@vip.sina.com

彭芸浩(1991-)，男，广东乐昌人，硕士研究生，2014年于长春理工大学获得学士学位，主要从事精密工作台设计及精密工作台系统建模、控制方面的研究。E-mail:1713142503@qq.com

(版权所有未经许可不得转载)

Dynamic hysteresis modeling and experimental verification of piezoelectric positioning stage

YANG Xiao-jing*， PENG Yun-hao， LI Yao

(SchoolofMechanicalandElectricalEngineering，KunmingUniversityofScienceandTechnology，Kunming650500，China)*Correspondingauthor，E-mail：xjyang@vip.sina.com

To improve the precision of rapid positioning of a piezoelectric positioning stage， a positioning model is established to characterize the relationship between driving voltage and output displacement of the platform. As the piezoelectric positioning stage for precision position in the fast and large stroke is not only affected by the hysteresis characteristics of the piezoelectric ceramics， but by the dynamic characteristics， this paper uses Bouc-Wen model to describe the hysteresis characteristics of piezoelectric ceramics， combines with the dynamic characteristics of the piezoelectric positioning stage to establish model， and lets the model reflect the dynamic characteristics and hysteresis characteristics of the platform. To verify the correctness of the model， the experimental equipment based on the piezoelectric micro displacement platform and the related driver is built， and model is verified by experiments， and a secondary development of monitor-control program is performed.The results show that, compared with the previous Bouc-Wen model,when proposed model in the maximum displacement output is 40 μm and the input voltage frequency is 40 Hz,the maximum error is reduced from 3.04 μm to 0.67 μm and the maximum relative error is 1.68%.The results show that the proposed model can better simulate the hysteresis characteristics and dynamic characteristics of the piezoelectric stage, and greatly improve the accuracy of the piezoelectric micro displacement platform in the fast and large stroke positioning.

piezoelectric positioning stage; dynamic characteristics; hysteresis characteristics; Bouc-Wen model; dynamic position

2016-04-10；

2016-05-21.

国家自然科学基金资助项目(No.51365021)

1004-924X(2016)09-2255-07

TP271.4；TH701

A

10.3788/OPE.20162409.2255