用于光学遥感器耐受卫星平台微振动环境地面测试的六自由度平台

顾营迎，霍　琦，李　昂，李大为，徐振邦，李　义，吴清文

(中国科学院 长春光学精密机械与物理研究所 机器人系统创新研究室，吉林 长春 130033)



用于光学遥感器耐受卫星平台微振动环境地面测试的六自由度平台

顾营迎*，霍琦，李昂，李大为，徐振邦，李义，吴清文

(中国科学院 长春光学精密机械与物理研究所 机器人系统创新研究室，吉林 长春 130033)

考虑空间卫星平台微振动环境对高分辨率空间光学遥感器成像质量的制约，提出了在地面测试光学遥感器耐受空间微振动环境裕度的六自由度激振平台的设计方案。建立了平台的运动学与动力学模型，推导出促动器音圈电机的传递函数并建立了Simulink模型。基于设计的模型研制了六自由度平台。对振动平台样机进行了振动加速度控制精度的验证实验，实验以典型的卫星平台微振动频率点为测试输入。实验结果表明平台振动频率为7～40 Hz时，其加速度输出相对误差可控制在7%以内。该平台借鉴了Stewart平台的并联构型，其结构简单、刚度大，振源输出精确可控，满足地面试验应用要求。

空间光学遥感器；空间微振动环境；六自由度平台；振动测试；地面测试

1　引　言

随着空间光学遥感器对地观测性能要求的不断提高，卫星平台微振动环境将成为制约空间光学遥感器观测性能进一步提升的主要因素之一[1]。来自卫星平台上其他设备的振动，以及外部空间环境温度的剧烈变化导致的卫星平台震颤等，都将导致空间光学遥感器对地成像性能降低，甚至达不到预期效果[2-4]。为此，国外一般从空间微振动环境在轨测量、振动模型及耦合路径建模分析和地面试验验证等方面，来研究空间平台微振动环境对遥感器性能指标的影响，从而克服空间微振动环境对光学遥感器的影响。NASA和德国航天局合作，利用德国的Astro-Spas小卫星平台进行了2次航天器在轨微振动环境实验，获取在轨航天器结构的微动力特性[5]。欧空局为了解决航天器微振动环境对未来高精度有效载荷的影响问题开发了PAX(The PDSE Accelerometer experiment)微振动测量系统[6]。该系统可监测在轨通讯卫星的微振动水平，获得未来设计高精度光学有效载荷的微振动实验数据，其次该系统还可以监测航天器上不同机构的动作。Eyerman和Sha等人对航天器微振动的扰动源进行了全面总结，认为航天器最大的扰动源是反作用飞轮扰动和热抖动[7]。Melody利用单个反作用飞轮扰动实验数据建立了反作用轮组的随机扰动模型[8]。Bialke对反作用飞轮扰动的来源、实验数据和数学建模进行了全面的论述[9]。Kim从仿真分析角度对航天器热扰动进行了研究[10]。NASA为测试JWST的卫星平台微振动环境耐受能力搭建了波前控制测试平台，该平台采用在光路中插入压电陶瓷驱动的快速偏转镜来模拟平台微振动[11]。

通过多根支腿、铰链，连接上、下平台形成上平台具有6个自由度的并联机构，最早始于Stewart的研究。人们把这种结构形式的并联机构统称为Stewart平台[12]。这种并联机构具有刚度高、结构紧凑、运动误差小等优点，得到了国内外的广泛重视。尤其在航空航天、大望远镜精密观测及运动模拟仿真等领域，该并联机构得到了广泛应用[13]。为了降低振动对光学成像仪性能造成的影响，美国空军研究实验室进行了卫星超静隔离技术在轨试验(SUITE)研究。该研究中使用并联机构平台进行隔振，能有效隔离空间六维振动。欧洲航天局将这种Stewart并联机构用于国际空间站上的精确指向平台，空间站在轨运行期间，该平台带动大气观测仪实现对地心的精确对准。国内哈尔滨大学、燕山大学、上海交通大学等也对Stewart平台进行了深入研究，并应用于精密指向、隔振、激振、运动仿真等领域的工程应用中，取得了较好的实验结果。

本文设计了一种用于光学遥感器成像性能耐受卫星平台微振动环境地面验证的六自由度振动平台。该平台借鉴了Stewart平台的并联构型作为振动机构，使平台结构简单，刚度大，具有6个振动自由度。将精密指向机构应用在振动生成上，可使振源输出精确可控。

2　六自由度平台系统设计

通过NASA对在轨卫星平台微振动的实测数据可知，卫星平台上的微振动频率主要集中在0.43～200 Hz内，而相应的加速度一般在10-5～10-3g内[14]。卫星平台的加速度值是由振动源的扰动力和平台自身的质量决定的，因此六自由度平台的振动输出频率及输出扰动力是本系统的关键指标。而系统输出的加速度值可以通过配重进行调节，可不作为设计指标。由此确定平台的主要设计指标如表1所示。

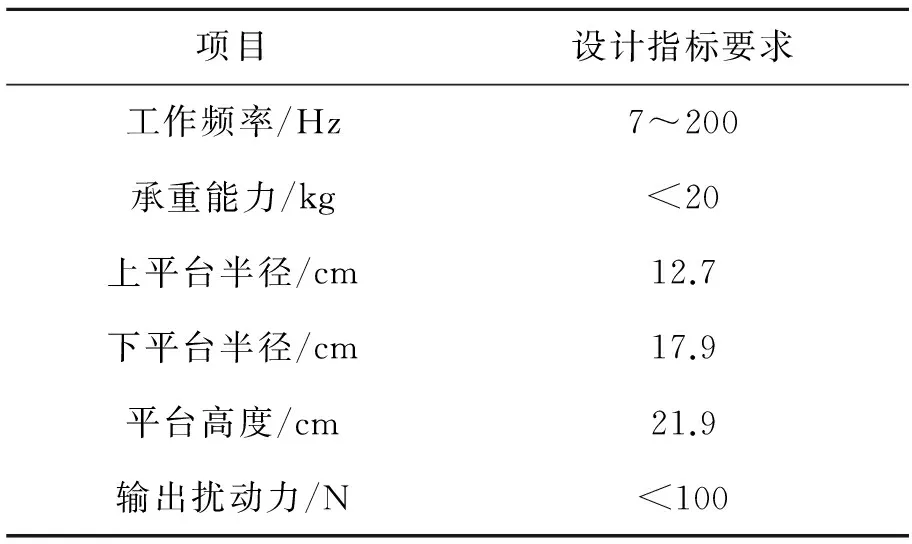
表1　平台设计指标

2.1平台系统架构

六自由度平台系统如图1所示，主要由3个子系统组成，包括上位机操作计算机系统，嵌入式中间系统和底层系统等。上位机操作计算机系统负责完成人机交互输入输出功能和运动学动力学的运动轨迹规划计算；嵌入式中间系统负责与上位机操作系统通讯，实时控制电机促动器和传感器采样处理；底层系统包括微振动平台机构，传感器硬件，电机促动器硬件和供电系统等。目前应用在六自由度并联平台上的电机促动器根据平台的应用领域和侧重点不同分为电磁驱动的，电机丝杠驱动的，压电驱动的，液压驱动的等。考虑到六自由度平台主要应用于产生模拟卫星平台的微振动环境，对振动复现的频率、带宽及输出力范围较为关注，因此选择电磁致动的音圈电机作为平台的力输出设备。

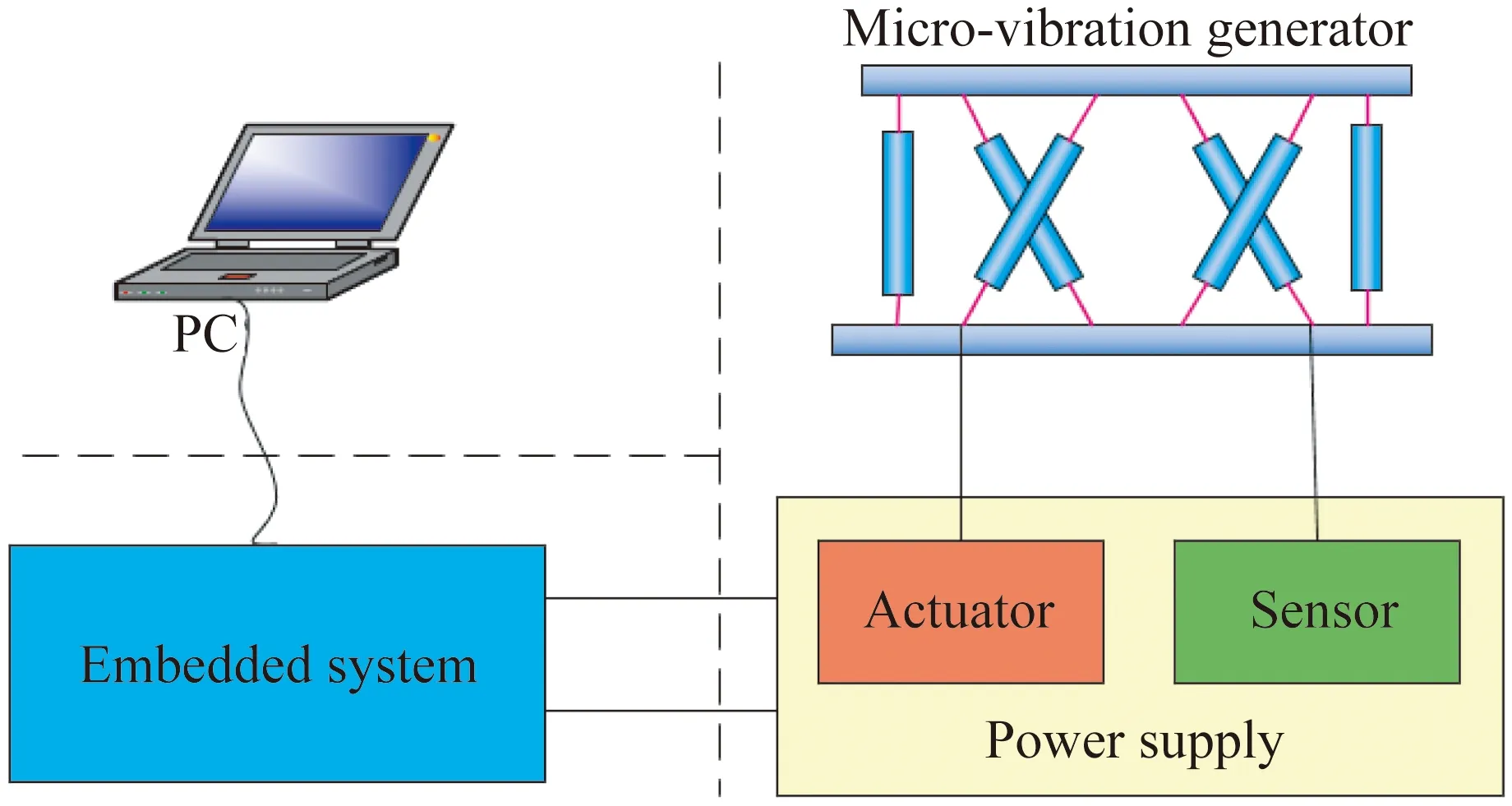
图1　振动平台系统架构

六自由度平台主要由上平台、下平台、平台支腿(包括上支腿、下支腿)及连接平台与平台支腿的铰链等组成。为了提高平台的稳定性和刚度，平台结构件的材料主要选用不锈钢。连接上平台与支腿的铰链采用具有3个转动自由度的铰链，连接下平台与支腿的铰链采用具有2个转动自由度的万向铰链。平台支腿应用音圈电机组装而成，可以等效为一个连接支腿上、下部分的具有1个自由度的运动副。

下平台一般作为固定的参考系部件，由此可知若不对平台各部分进行铰链约束，则整个系统含有13个运动部件，包括1个上平台、6个上支腿、6个下支腿，每个部件具有6个自由度，这样系统总的自由度共78个。经过铰链约束后，对于一根支腿上的3个铰链来说，将约束12个自由度，则整个系统被铰链连接后将约束72个自由度。最终六足平台的上平台将有6个自由度，满足预期的自由度设计。

2.2平台的运动学和动力学建模

为了能够精确控制六自由度平台的频率、振幅和加速度，需建立精确合理的运动学和动力学模型。运动学分析建模可以解决上平台和6根支腿之间的位置、速度和加速度的关系[15]；动力学建模分析可以解决上平台和6根支腿之间的力、力矩的关系。

相对于运动学分析建模，并联机构的动力学建模比较复杂，主要由于整个系统是结构封闭的并且有运动约束。目前有很多方法用来建立并联结构的动力学模型，如牛顿-欧拉法，拉格朗日法和凯恩方法等。但是所有的方法都是对同一个物理系统的描述，这些方法在描述结果上是等效的，只是建模的切入点不同，建模的难易程度和计算量方面有区别。如何减小建模的计算量以使模型更方便实时更新计算仍是当前并联机构动力学建模的前沿研究领域[16-18]。

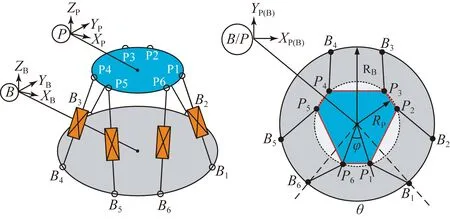
图2　微振动平台坐标系

六自由度微振动平台坐标系如图2所示，图中{P}坐标系是上平台坐标系，固定在上平台上，{B}坐标系是下平台坐标系，同时也作为惯性坐标系。Pi(i=1～6) 是连接支腿和上平台的结点，Bi(i=1～6)是连接支腿和下平台的结点，Rp是上平台的半径，Rb为下平台的半径，φ为P6，P1与圆心间的夹角，θ为B6，B1与圆心间的夹角。

在惯性坐标系{B}下，六自由度平台的第i个促动器的运动学方程可描述为：

Bli=Bt+Bpi-Bbi=

(1)

(2)

(3)

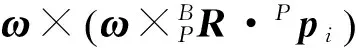
(4)

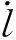
根据物理意义，促动器速度可以表示为B坐标系下的促动器滑动速度和角速度的函数：

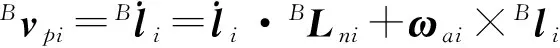
(5)

式中：ωai为促动器的角速度。

用Blni对式(5)进行叉乘，同时忽略促动器的绕轴线旋转运动(ωai·Blni=0)有：

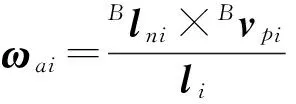
(6)

促动器的角加速度为：

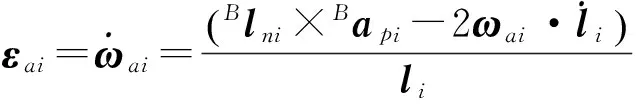
(7)

对于平台的动力学模型，将上平台简化为刚性体，同时忽略促动器自身的惯量用牛顿欧拉方法[19]来进行建模分析：

kJTJq=JTΓ，

(8)

考虑促动器自身惯量的情况下，完整的六自由度平台动力学模型[20]可以表示为：

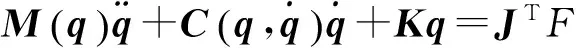
(9)

上式两侧同时左乘J-T，即可得出促动器电机对应的输出激励力：

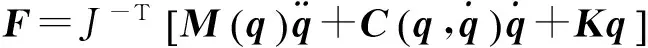
(10)

2.3平台促动器建模

平台促动器的动力输出源选用音圈电机，该音圈电机在固定磁场的作用下其输出的力与通过电机绕组的电流成正比。音圈电机具有直线输出位移可达到几十毫米、可以输出力的范围宽、具有较高的工作带宽等特点，非常适合作为激振、隔振的主动力输出设备。

音圈电机的电流与输出力之间的转换关系满足洛仑兹定理。在固定的磁场和几何约束条件下，电机的输出力FB与电流I满足：

FB=KFI，

(11)

式中：KF为音圈电机的输出力常数。

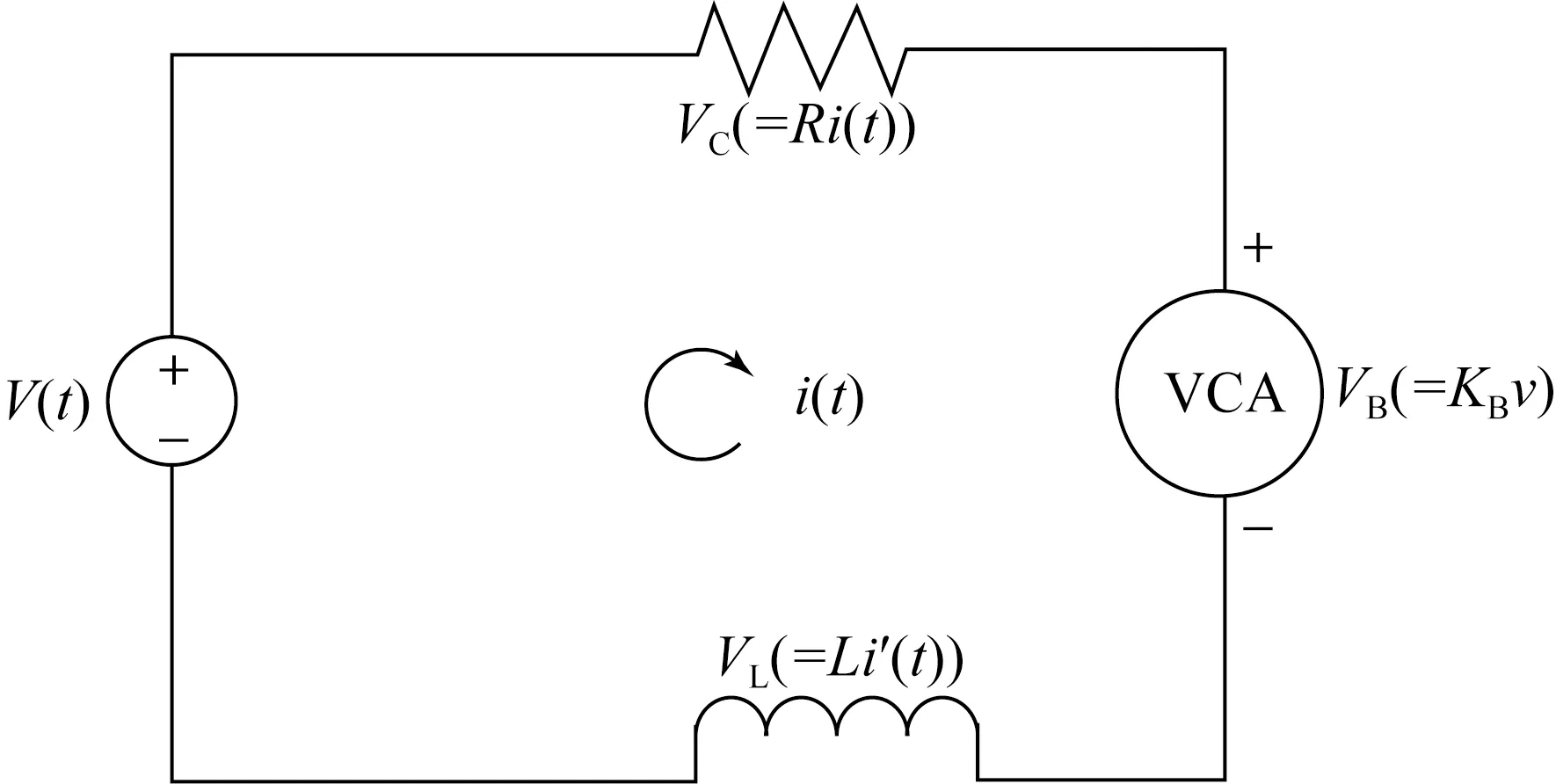
图3　音圈电机等效电路

图3所示为音圈电机的等效电路，当电压V(t) 作用在电路两端时，相应的会有电流i(t)流过电阻R，同时音圈电机还会产生一个反电动势VB，该反电动势与电机动子与定子之间的相对速度成正比，比例系数用KB表示，由于电感L的存在，作用在电感上的电压可用VL=Li′(t)表示。最终，根据基尔霍夫定理可得到式(12)，对该式进行拉普拉斯变换得到式(13)：

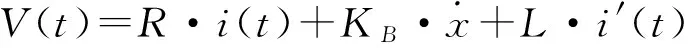
(12)

V(s)=R·I(s)+KB·sX(s)+L·sI(s).

(13)

音圈电机工作中的物理机械模型如图4所示，有4个力作用在电机的定子上，它们分别为弹簧的弹力，阻尼力，惯性力和洛仑兹力。电机动子的运动特性由式(14)确定。结合式(11)，式(14)可以写为(15)。将式(15)进行拉普拉斯变换得到式(16)。进一步，根据式(13)和式(16)可以得到式(17)和式(18)所示的传递函数。图5所示为根据式(13)和式(16)在Simulink下建立的音圈电机模型：

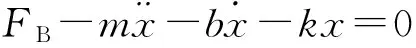
(14)

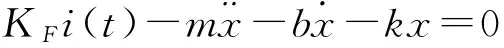
(15)

KFI(s)+(-ms2-bs-k)X(s)=0，

(16)

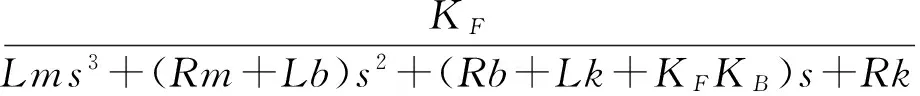
(17)

(18)

图6所示为音圈电机组装后的促动器试验组件，音圈电机的详细技术参数如表2所示，为了约束音圈电机其他自由度，在组装中增加了弹簧片，因此在弹簧片的约束下音圈电机只有沿轴线运动的自由度。

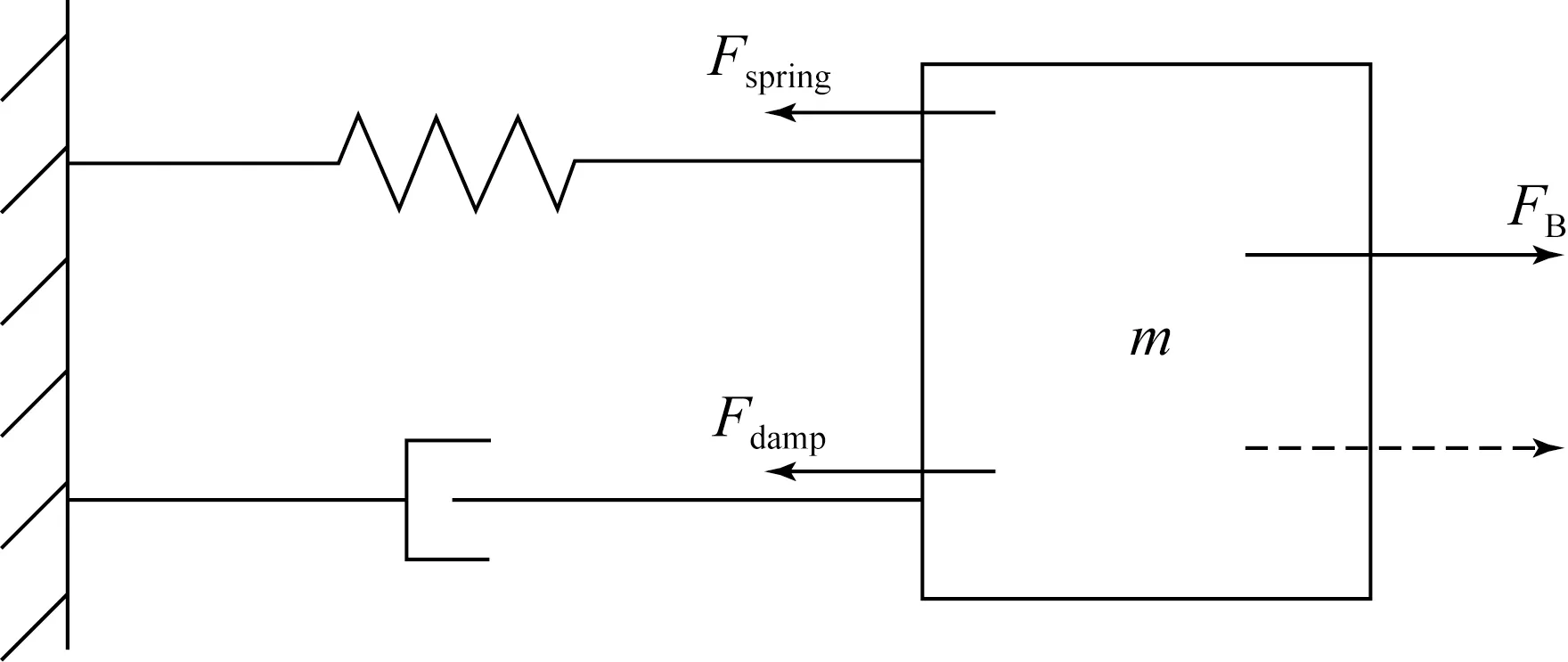
图4　音圈电机物理模型

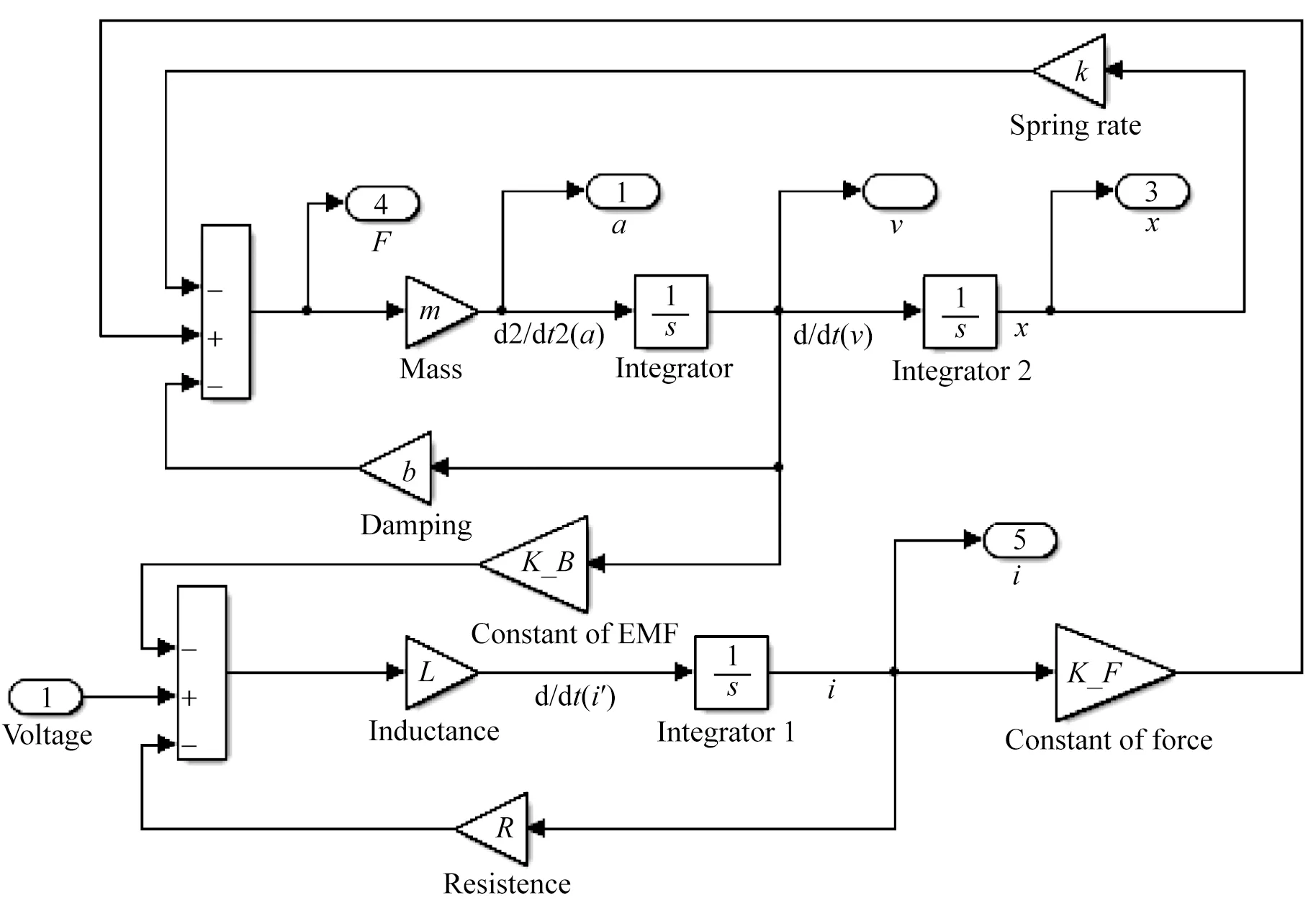
图5　音圈电机Simulink模型

图6　音圈电机构建的促动器

3　实验结果与讨论

图7所示为根据以上模型设计研制的六自由度振动平台，该平台由上平台、下平台、力传感器、加速度传感器、控制系统、电源系统和接口转换电路组成。为了验证平台控制输出振动的能力，实验设计为选取典型的卫星平台微振动频率点作为平台输出的振动频率[14]，用加速度传感器测定平台设定输出加速度的幅值与实测幅值的相对误差来评价振动台的性能。

试验中振动的型式为正弦振动，同时选取具有典型参考价值的平动x方向为测试方向，对于整个振动平台，x方向振动控制与y方向振动控制在结构上是对称的，而z方向振动控制又相对x方向或y方向简单。试验结果如表3所示。从实验结果可以看出，平台在3 Hz和48 Hz 处不稳定，同时在5 Hz和43 Hz处加速度输出相对误差较大，这主要是由于以上频率点接近了平台的一阶和二阶固有频率导致的。另外实验结果表明平台在7～40 Hz内振动控制相对误差达到了7%以内，满足振动源应用要求。通过试验结果可以看出利用本文直接建模控制平台振动的方法在60～166 Hz内误差较大，不能满足振动控制的要求，经过分析这主要是由于为了简化计算将平台组件都考虑为刚性体，同时忽略了促动器自身的惯量，但是在高频段内这种假设和处理是不当的，刚性体会体现出柔性体的特性，同时促动器自身惯量的影响在高频段内也是不可忽略的。这一问题可以通过实验数据来不断修正模型，同时引入闭环反馈控制来逐步解决。

图7　实验物理平台

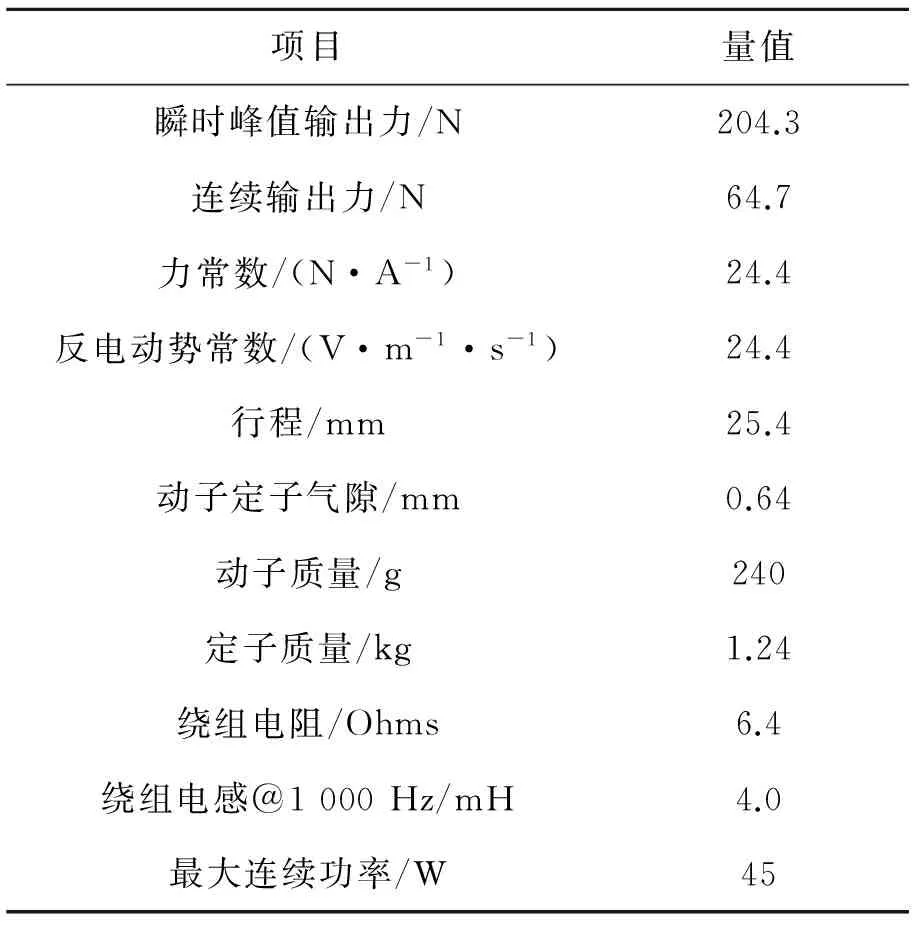
项目量值瞬时峰值输出力/N204.3连续输出力/N64.7力常数/(N·A-1)24.4反电动势常数/(V·m-1·s-1)24.4行程/mm25.4动子定子气隙/mm0.64动子质量/g240定子质量/kg1.24绕组电阻/Ohms6.4绕组电感@1000Hz/mH4.0最大连续功率/W45

表3典型频率下平台沿x方向平动的加速度控制实验结果

Tab.3Experiment results of reproduced vibrational acceleration by the physical platform along axisxin some typical frequencies

频率/Hz设定值/(m·s-2)实测值/(m·s-2)相对误差/%31不稳定—511.4444710.94-61711.0772010.97-32210.95-53810.95-54010.95-54310.4-60481不稳定—5312.611616011.99998011.616116612.07107

4　结　论

针对空间卫星微振动环境对高分辨率光学遥感器成像质量的制约因素逐渐凸显的问题，本文论述了一种应用于地面测试验证光学遥感器耐受空间微振动环境裕度的六自由度激振平台的研制方案，进行平台的运动学与动力学建模分析，建立促动器音圈电机的Simulink模型，最后对振动平台样机进行了振动加速度控制精度的验证实验，以典型的卫星平台微振动频率点为测试输入，实验结果表明振动平台在7～40 Hz内控制相对误差在7%以内，满足设计要求，同时也为进一步改进扩宽平台的振动频率范围提供了基础试验数据和方法。

[1]许博谦， 郭永飞， 王刚. 测量空间相机像移量的联合变换相关器的改进[J]. 光学 精密工程， 2013， 22(6): 1418-1423.

XU B Q， GUO Y F， WANG G. Improvement of joint transform correlator for measurement of space camera image motion [J].Opt.PrecisionEng.， 2013， 22(6): 1418-1423.(in Chinese)

[2]KRIST J E. High-contrast imaging with the Hubble Space Telescope: performance and lessons learned[C].SPIEAstronomicalTelescopes+Instrumentation.InternationalSocietyforOpticsandPhotonics， 2004:1284-1295.

[3]杨剑锋， 徐振邦， 刘宏伟，等. 光学有效载荷在轨隔振器的设计[J]. 光学 精密工程， 2014，22(12): 3294-3302.

YANG J F， XU ZH B， LIU H W，etal.. Design of vibration isolator for optical payload on orbit [J].Opt.PrecisionEng.， 2014，22(12): 3294-3302.(in Chinese)

[4]虞自飞， 周徐斌， 申军烽， 等. 卫星飞轮隔振与吸振联合减振系统设计[J]. 光学 精密工程， 2014， 22(4): 897-903.

YU Z F， ZHOU X B， SHEN J F，etal.. Design of joint vibration reduction system combined isolation and absorbtion for flywheel [J].Opt.PrecisionEng.， 2014， 22(4): 897-903.(in Chinese)

[5]LEVINE M B， LEVINE M B. Interferometry program flight experiments: IPEX Ⅰ and Ⅱ[J].ProceedingsofSPIE-TheInternationalSocietyforOpticalEngineering， 1998:707-718.

[6]DYNE S J C， TUNBRIDGE D E K， COLLINS P P. The vibration environment on a satellite in orbit [C].HighAccuracyPlatformControlinSpace，IEEColloquiumon，IET， 1993:12/1-12/6.

[7]EYERMAN C E. A systems engineering approach to disturbance minimization for spacecraft utilizing controlled structures technology [D].MassachusettsInstituteofTechnology， 1990.

[8]MELODY J W. Discrete-frequency and broadband reaction wheel disturbance models [J].InterofficeMemorandum， 1995: 3411-95-200csi.

[9]BIALKE B. A compilation of reaction wheel induced spacecraft disturbances [C].Proceedingsofthe20thAnnualAASGuidanceandControlConference， 1997.

[10]KIM Y A. Thermal creak induced dynamics of space structures [J].MassachusettsInstituteofTechnology， 2010.

[11]LIGHTSEY P A， CHRISP M. Image quality for large segmented space telescopes [J].ProceedingsofSPIE-TheInternationalSocietyforOpticalEngineering， 2003， 4850.

[12]STEWART D. A platform with six degrees of freedom [J].ARCHIVEProceedingsoftheInstitutionofMechanicalEngineers， 1965， 180:371-386.

[13]DASGUPTA B， MRUTHYUNJAYA T S. The Stewart platform manipulator: a review [J].Mechanism&MachineTheory， 2000， 35(1):15-40.

[14]ROGERS M J B， VOGT G L， WARGO M J. Microgravity: a teacher’s guide with activities in science， mathematics， and technology [J].UltrasoundinMedicine&Biology， 1997， 1(1):151-168.

[15]张景旭， 安其昌， 李剑锋， 等. 基于机构条件数的30 m望远镜三镜Stewart平台[J]. 光学 精密工程， 2014， 22(4): 890-896.

ZHANG J X， AN Q CH， LI J F，etal.. Third mirror Stewart platform of TMT based on mechanism condition number [J].Opt.PrecisionEng.， 2014， 22(4): 890-896.(in Chinese)

[16]ABDELLATIF H， HEIMANN B. Computational efficient inverse dynamics of 6-DOF fully parallel manipulators by using the Lagrangian formalism [J].Mechanism&MachineTheory.， 2009， 44(1):192-207.

[17]WANG J， WU J， WANG L，etal.. Simplified strategy of the dynamic model of a 6-UPS parallel kinematic machine for real-time control [J].Mechanism&MachineTheory.， 2007， 42(42):1119-1140.

[18]SOKOLOV A， XIROUCHAKIS P. Dynamics analysis of a 3-DOF parallel manipulator with R-P-S joint structure [J].Mechanism&MachineTheory.， 2007， 42(5):541-557.

[19]DASGUPTA B， MRUTHYUNJAYA T S. A newton-euler formulation for the inverse dynamics of the stewart platform manipulator [J].Mechanism&MachineTheory.， 1998， 33(8):1135-1152.

[20]OFTADEH R， AREF M M， TAGHIRAD H D. Explicit dynamics formulation of stewart-gough platform: a newton-euler approach [C].IntelligentRobotsandSystems(IROS)， 2010IEEE/RSJInternationalConferenceonIEEE， 2010:2772-2777.

顾营迎(1984-)，男，天津人，博士，副研究员，2013年于中国科学院大学获得博士学位，主要从事机器人视觉感知与控制方面的研究。E-mail:18686681605@163.com

霍琦(1988-)，男，山东菏泽人，硕士，实习研究员，2011年、2014年于哈尔滨工程大学分别获得学士、硕士学位，主要从事自动控制、电子学设计方面的研究。E-mail:514590249@qq.com

(版权所有未经许可不得转载)

Six DOF platform applied in ground test of optical remote sensor alleviation margin in satellite micro-vibration environment

GU Ying-ying*， HUO Qi， LI Ang， LI Da-wei， XU Zhen-bang， LI Yi， WU Qing-wen

(InnovationLabofSpaceRobotSystemChangchunInstituteofOptics，FineMechanicsandPhysics，ChineseAcademyofSciences，Changchun130033，China)*Correspondingauthor，E-mail：18686681605@163.com

As the micro-vibration of a satellite platform restricts the imaging quality of a high-resolution space optical remote sensor， this paper designs a six DOF(Degree of Freedom) platform for the ground test of optical remote sensor alleviation margin in satellite micro-vibration environment. The kinematics and dynamics models of the platform were constructed， and the transfer function， Simulink model of a voice coil actuators were derived. Based on the models， the platform with six DOFs was manufactured. A confirmatory experiment on the vibration acceleration control accuracy of the platform was carried out， in which the micro-vibration frequency of the typical satellite was taken as the input signal. The results show that the relative error of output acceleration has been controlled in 7% in frequencies from 7 Hz to 40 Hz. The platform takes the parallel construct of the stewart model， it has advantages in simpler structure， bigger stiffness and a controllable vibration source， and obtained results meet the requirements of the ground test applications.

space optical remote sensor; micro-vibration environment in space; six DOF platform; vibration test; ground test

2015-12-11；

2016-01-20.

国家自然科学基金资助项目(No.11302222)

1004-924X(2016)09-2200-08

V423.6；V416.21

A

10.3788/OPE.20162409.2200