用于光纤光栅曲线重建算法的坐标点拟合

章亚男，肖　海，沈林勇

(上海大学 机电工程与自动化学院，上海 200072)



用于光纤光栅曲线重建算法的坐标点拟合

章亚男*，肖海，沈林勇

(上海大学 机电工程与自动化学院，上海 200072)

以光纤布拉格光栅(FBG) 曲线传感器在结肠中的形状检测为背景，提出了一种基于Frenet标架的坐标点拟合算法来提高光纤光栅曲线重建算法的精度。首先，将相互之间呈90°的四根光纤光栅贴在一根形状记忆合金(SMA Styrene Maleic Anhydride)基材周围，形成一根直径为3 mm，长度为900 mm的光纤光栅曲线传感器。接着，将该曲线传感器分别放置在毫米方格纸以及圆柱体上进行二维和三维曲线的重建。通过曲线重建软件读出每个数据采集点的重建坐标值，并与通过方格纸读出的标准坐标值对比得出重建误差， 从而得出两种坐标点拟合方法的优劣。结果表明：使用基于Frenet标架的坐标点拟合算法可有效提高重建精度。对提出的算法与常用的曲线重建算法进行了比较， 结果显示：在接近光纤光栅应变极限的情况下，使用基于Frenet标架的坐标点拟合算法在单方向上能够比原算法平均减小约3.5%～5.5%的误差，为进一步提高光纤光栅形状传感系统的精度奠定了基础。

光纤光栅；曲线重建算法；坐标点拟合；Frenet标架；形状检测

1　引　言

近年来，随着智能传感技术、生物医学工程、计算机图形学等学科的发展，传统医疗器械的功能不断增强。在无创及微创医疗领域，大多数场合都需要用到内窥镜作为手术检查工具，如结肠检查。不过，由于工作环境的复杂性以及形状不可视等特点，传统内窥镜在介入过程中容易发生刮擦、穿刺组织等危及病人生命的情况。因此，对穿入人体管道内窥镜的形状探知是一项紧迫的任务。光纤光栅传感器为解决内窥镜的形状感知提供了一条可行的技术途径，所以成为了近十多年来的研究开发热点。作为新型传感单元，国外的研究机构利用FBG在组织活检的探针导航[1]、心脏主动脉瓣植入[2]、脊柱变形检测[3]等方面展开了一系列研究。上海大学智能医疗机器人研究小组也对基于光纤光栅的智能内窥镜感知系统进行了一系列研究[4-6]。这些研究表明，光纤光栅曲线传感器能够对结肠部位进行形状重建，但传感器末端的定位误差依然有10%[7]，难以满足实际要求。

在传感器曲线重建算法方面，国内外采取的基本思路如下：通过将采集到的FBG信号转化为曲率，再利用微分几何与计算机图形学知识拟合出曲线形状。文献[8]描述了离散点曲率的连续化方法以及由曲率积分求曲线位置的拟合方法，文献[9]提出了基于曲率信息的空间曲线拟合方法，文献[10]使用OpenGL显示技术实现了对传感曲线的实时重建。上述研究中使用的曲线拟合算法较繁琐且精度较低，而针对基于曲率信息的曲线拟合算法的精度改进研究尚不多见。

本文以FBG曲线传感器在结肠中的形状检测为背景，从曲线重建算法出发提出了一种新的基于离散曲率信息的坐标点拟合方法。对FBG曲线传感器摆成的二维及三维实际曲线进行了多种坐标点拟合法的对比研究，得出精度较高的算法，并计算出重建精度的提高程度。

2　FBG传感系统的构成及其工作原理

2.1光纤光栅的工作原理

图1为光纤光栅的工作原理图。首先在光纤外放置相位模板，再利用紫外线照射，使光纤内产生栅格，从而改变了纤芯区的折射率，并让折射率产生周期分布。宽带光在光纤中传输时遇到栅点后将在相应的频率上得到反射，其余频率的光则透射出，这样便可任意刻出需要的反射频率光的栅点。光纤布拉格光栅(Fiber Bragg Grating，FBG)的反射波长与折射率周期的关系为[11]：

λC=2·Λ·neff，

(1)

其中：Λ为光栅的栅格周期，neff是等效折射率。受外界力以及温度变化的影响，FBG易发生反射波长漂移。应力作用导致FBG折射率变化，进而改变了有效弹光系数；温度变化导致FBG热光系数与热膨胀系数的改变。FBG的反射波长变化与应变以及温度的关系如下：

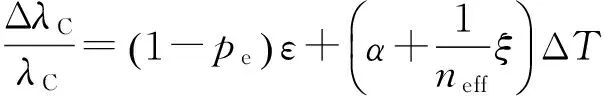
(2)

其中：ε是FBG轴向应变，pe为有效弹光系数，α为热膨胀系数，ξ为热光常数。这里不考虑温度变化，于是式(2)可简化为：

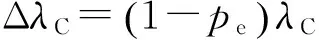
(3)

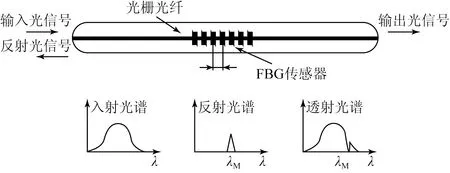
图1　光纤光栅传感器的工作原理图

2.2曲线传感系统设计

实验系统由传感器模块、解调系统、显示硬件与软件开发环境几部分组成，如图2所示。在传感器设计方面，考虑到需要同时采集多个点的光栅中心波长以及光纤光栅具有的空分和波分特性，决定使用4根FBG围绕在一根镍钛记忆合金周围，并且相互间呈90°关系。每根光纤上布置5个光栅点，且每个光栅点的中心波长都不相同，光栅点间距为200 mm。1、2号光纤中光栅的位置与3、4号光纤中光栅的位置相互交错，传感部分总长为900 mm。一组相互垂直的光栅点可确定一个空间点的曲率信息，一共可确定10个空间点的曲率信息。

(a)光纤光栅传感网络示意图

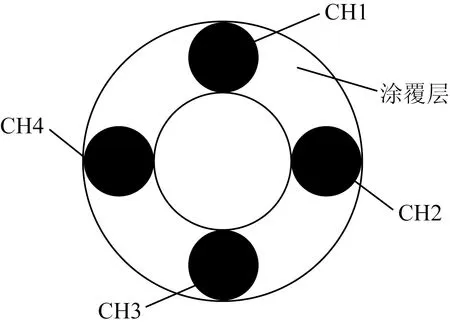
(b)光纤光栅间的位置关系图

解调系统的采样频率为250 Hz，共有4条通道，每条通道可解调的波段为1 520～1 570 nm，能够满足传感器所需的条件。解调系统通过以太网协议与显示器硬件连接。实验软件是运用VS2010自带的MFC框架功能编写的应用程序，结合了OpenGL显示技术与Socket数据传输技术。通过获取正交光栅点的波长信息，结合曲率样条插值与三维曲线重构算法实现了传感器曲线的可视化显示。

2.3曲线传感器弯曲曲率算法

图3为纯弯曲状态下基材与FBG的应变关系。对于圆截面的细长弹性体而言，其曲率和应变之间存在以下关系[6]：

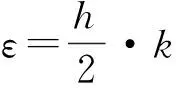
(4)

其中：k为弹性体的弯曲曲率，h为上下两个FBG的安装中心的距离。可看出应变和曲率呈线性关系，将式(4)代入式(3)可得到FBG中心波长变化量与曲率的关系：

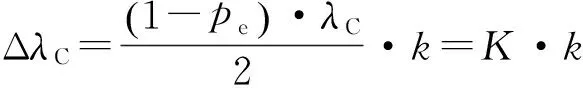
(5)

其中：pe和λC为常数，则光栅的中心波长变化量ΔλC和弹性体的曲率k呈线性关系。K为曲率灵敏度系数，可通过标定得出。对每个光栅点全部测量出应变状态下的波长值，再与无应变状态下的波长值相减后代入式(5)，即可求出相应的曲率。每一个空间检测点的合成曲率ksyn为：

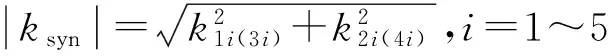
(6)

其中：k1i，k2i，k3i和k4i分别代表4根光纤上不同光栅点测量并计算出的曲率值。同时可算出合成曲率与曲率分量的角度，从而为曲线坐标拟合打下了基础。

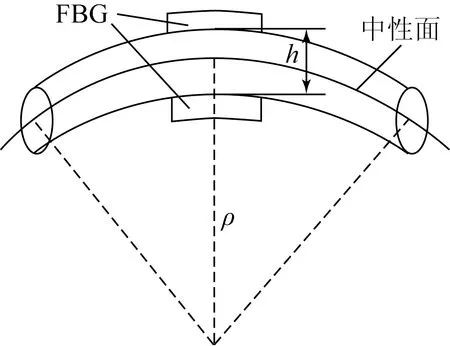
图3　传感器纯弯曲示意图

图4为一根光纤在笔直状态下的光栅中心波长频域图。从图中可以看出，5个光栅点的中心波长相隔了一定的距离，这是为了防止相邻两个光栅点的中心波长在漂移后发生交错重叠的现象。

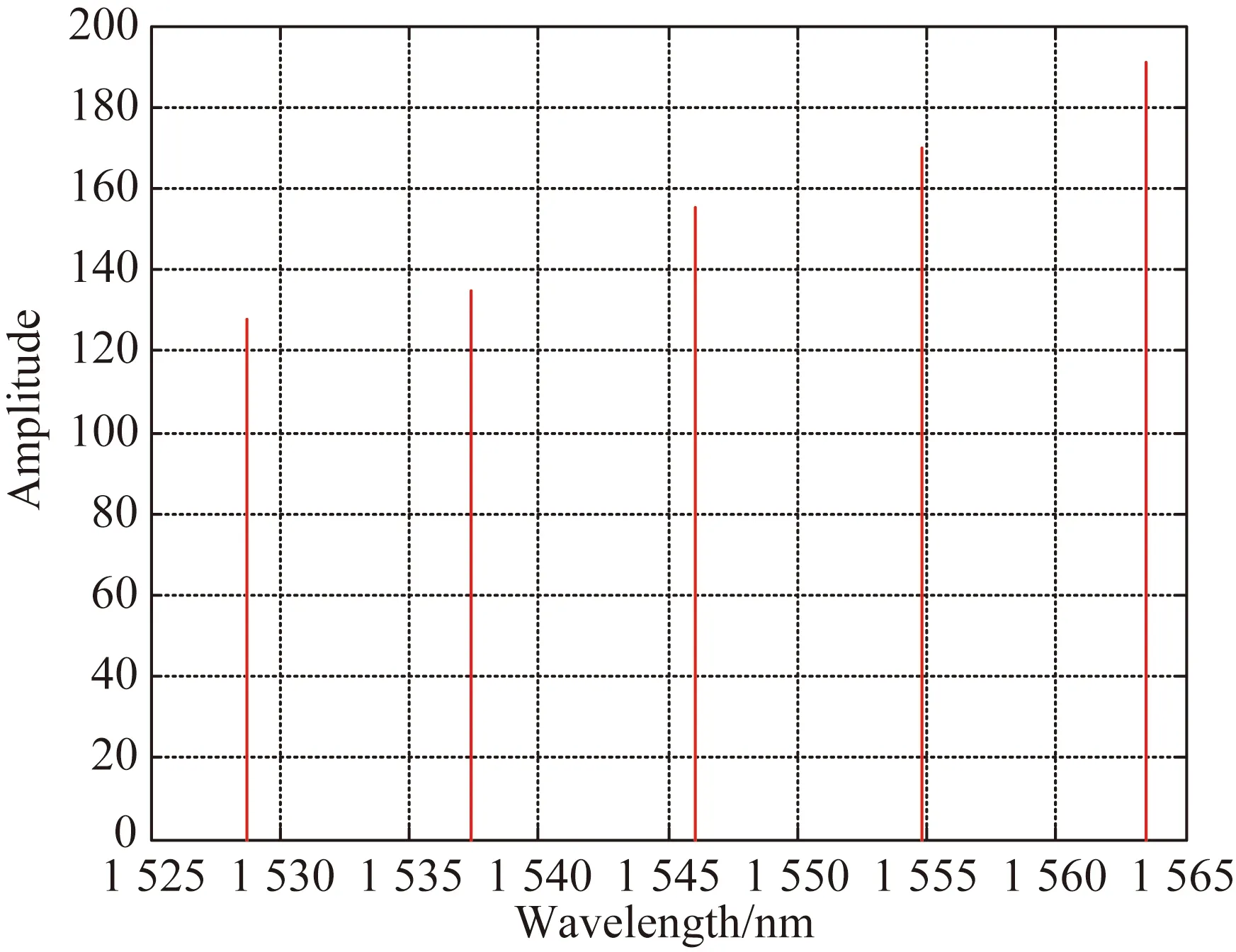
图4　光纤上各个光栅点的中心波长频域图

3　基于曲率信息的曲线重建关键算法

3.1离散曲率连续化分析

求出每一个光栅检测点的弯曲曲率后，需使用一定的曲率连续化方法求出曲线上更多点的曲率，以便之后采用坐标点拟合算法拟合出足够多点的坐标值。目前采用的曲率连续化插值法为线性插值法以及B样条曲线插值法[12]。前者的运算时间较快，但由于曲率分割简单，分割点的连接处不平滑，与实际产生的曲率曲线有一定的差距。后者解决了分割点连接处的光滑问题，但10个离散曲率检测点的曲率不全在拟合出的曲率连续化曲线上，会产生一定的拟合误差。为了解决以上问题，这里采取了三次样条曲率插值法[13]。

假设曲率与弧长的关系为：

k(S)=ai+bi×(S-Si)+ci×(S-Si)2+

di×(S-Si)3，

(7)

式中：ai，bi，ci和di为4个待定系数，Si为第i个分割点离起点的弧长。曲线在第i个分割点满足以下关系：

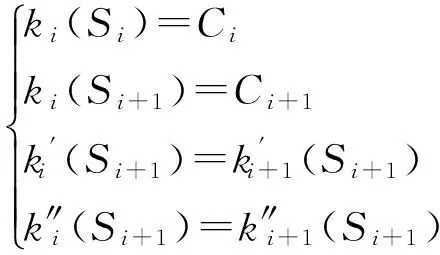
(8)

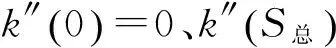
3.2坐标点拟合算法的研究

坐标点拟合的基本思路是根据分割点建立若干运动坐标系，坐标系原点即为曲线微段的起始点。在运动坐标系中建立曲线微段的密切平面，在密切平面内根据曲率信息完成微段末端点的坐标计算。将若干密切平面内的二维曲线连接则构成了一条三维曲线。目前，常用的拟合算法将曲率方向作为运动坐标系的坐标轴，现提出一种基于Frenet标架的拟合算法。

3.2.1曲率方向为坐标轴的坐标点拟合算法

如图5所示，绝对坐标系为o-a0b0c0，其中c0方向沿着曲线初始微段的切线方向，a0，b0方向分别为曲线微段曲率的两个分量方向，在弯曲变化的曲线上建立运动坐标系o-abc，在初始状态下运动坐标系的方向定义与绝对坐标系的一致。运动坐标系中由ka和kb合成得到k，k的方向与空间曲线在该点处的单位法向量β方向相同，即k=|k|β。

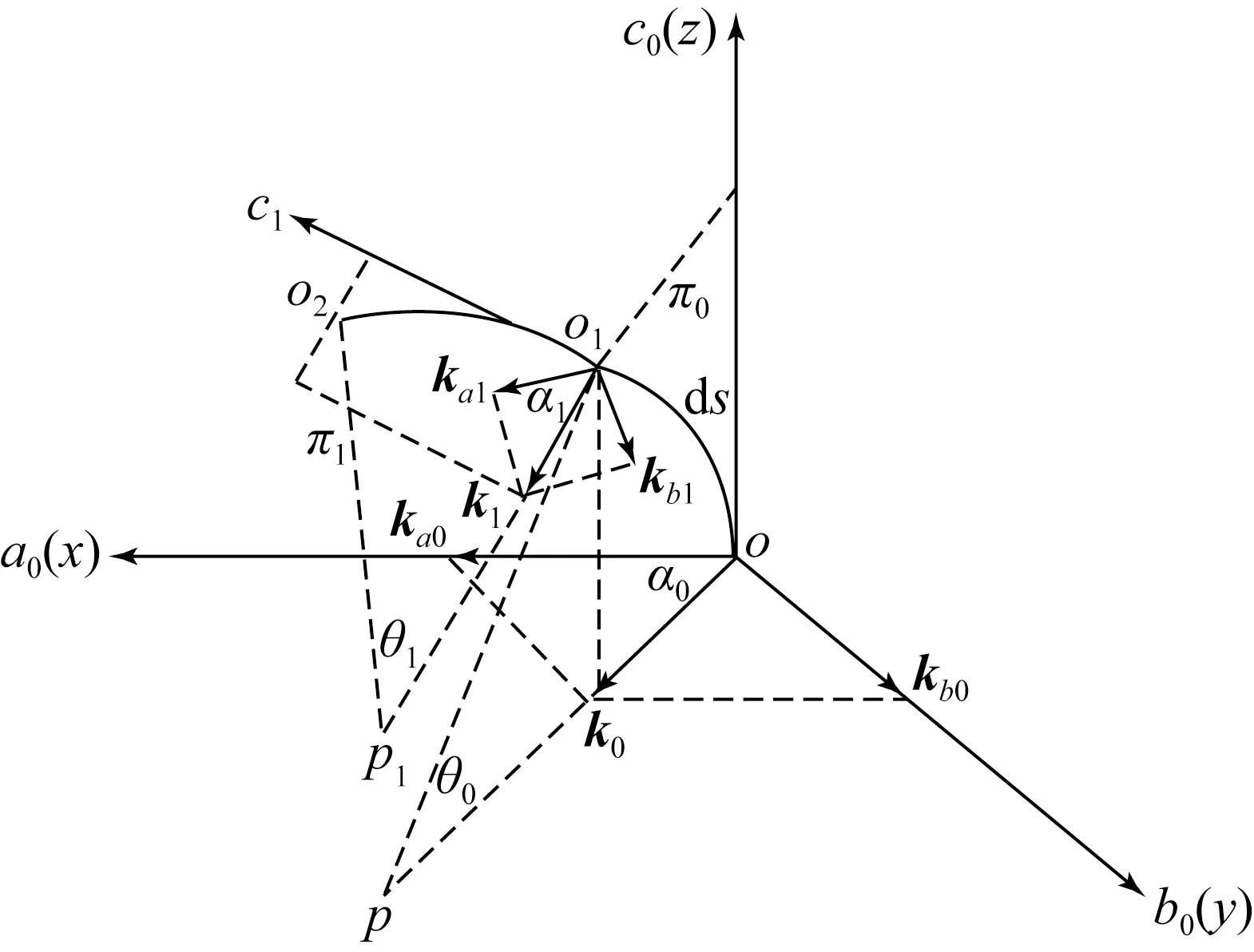
图5　曲率方向与坐标轴重合时的拟合原理

Fig.5Fitting principle when curvature directions is coincident with coordinate axes

曲线微段的密切平面由微段的切向量和法向量确定，因此图4中的π0和π1平面分别为两个微段的密切平面。将绝对坐标系记作{A}，第i点处的运动坐标系记作{Bi}、曲率分量分别记作kai和kbi。通过kai和kbi可求出合成曲率ki，同时可求得ki与kai之间的夹角αi。得出点i的ki和αi后，便可确定下一点i+1在运动坐标系{Bi}中的坐标。这里假设i+1点在绝对坐标系中的坐标为{xi+1，yi+1，zi+1}，该处的运动坐标系为{Bi+1}。第i点的曲率绝对值为ki，弧长假设为ds，则对应的圆弧圆心角为θi=ds×ki，通过图4可计算出i+1点在{Bi}中的坐标为：

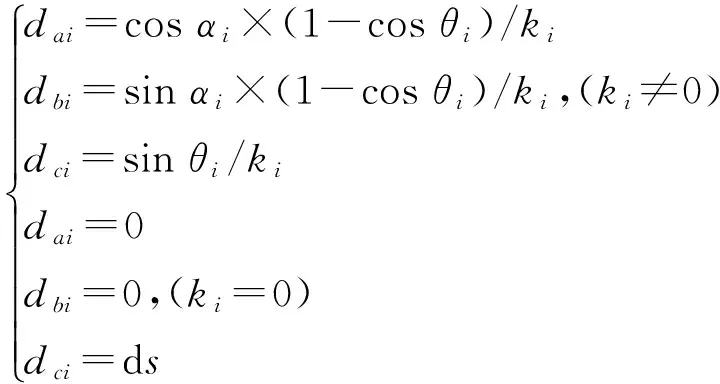
(9)

接下来可以求出i+1点在绝对坐标系{A}的值。设i点处的绝对坐标系{A}转换到相对坐标系{Bi}的齐次转换矩阵为[Ti]，即：

{Bi}=[Ti]{A}.

(10)

假设第i-1点到第i点的推导中已经求得4×4 齐次矩阵[Ti]-1，当最初绝对坐标系与相对坐标系重合时，[Ti]-1为单位矩阵。则i+1点在{A}中的坐标可表示为：

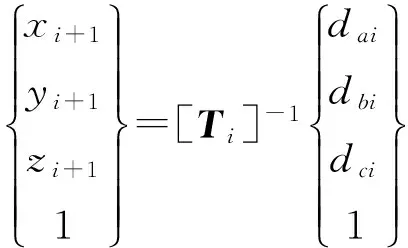
(11)

最后，建立下一点i+1的运动坐标系{Bi+1}以及确定i+1点的绝对坐标。{Bi+1}坐标系的原点就是i+1点，在{Bi}中的坐标为{dai，dbi，dci}，{Bi+1}的c轴方向就是i+1点处曲线的切线方向。设{Bi}转换到{Bi+1}的齐次变换矩阵为[ti+1]，则有：

{Bi+1}=[ti+1]{Bi}.

(12)

[ti+1]的转换步骤如下：

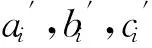
(3)将新坐标绕着c″i轴旋转-αi，使得下一点i+1的曲率方向ki+1与kai+1的夹角保持不变，相应的转换矩阵记作[Rci，-αi]；

(4)此时坐标轴旋转完成，平移一个向量{dai，dbi，dci}即可得到[ti+1]。

记[Ri+1]=[Rci，αi][Rbi，θi][Rci，-αi]，则[ti+1]为：

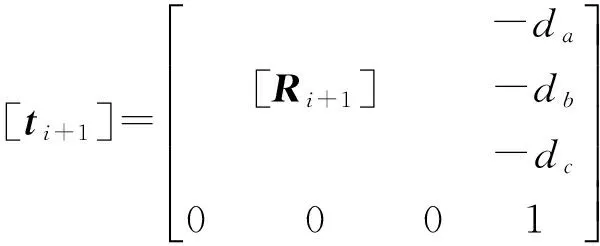
(13)

设{A}转换到{Bi+1}的齐次变换矩阵为[Ti+1]，即：

{Bi+1}=[Ti+1]{A}.

(14)

由式(10)、式(12)和式(14)可得出：

[Ti+1]=[ti+1][Ti].

(15)

通过式(15)可求出i+1点的绝对位置坐标。不断循环以上步骤便可求出每一个微段末端点的绝对坐标，将这些点全部连起来就完成了三维曲线的重建。

3.2.2基于Frenet标架的坐标点拟合算法

在微分几何中，曲线描述通常采用Frenet坐标标架[14]。如图6所示，T为切向量方向；N为主法线方向，指向微段曲率的方向；B为副法线方向，三者关系为：B=T×N。

假设第i段曲线位于XOZ平面内，可算出坐标从Oi点移动至Oi+1点的平移量：

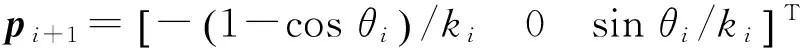
(16)

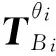
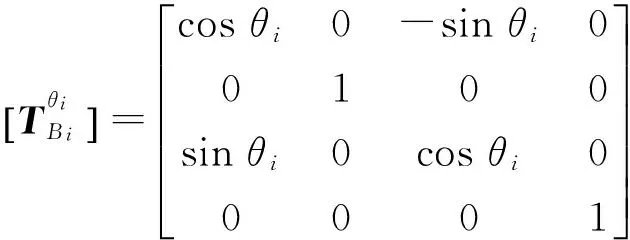
(17)

接着将坐标系沿着Ti轴旋转Δφi+1，此值为非负数，由下式求出：

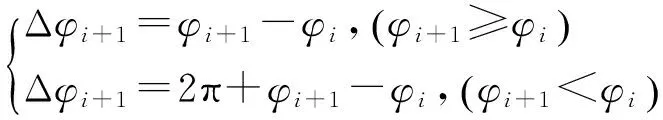
(18)

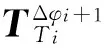
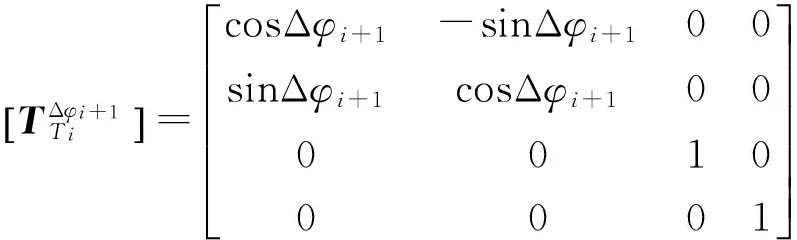
(19)

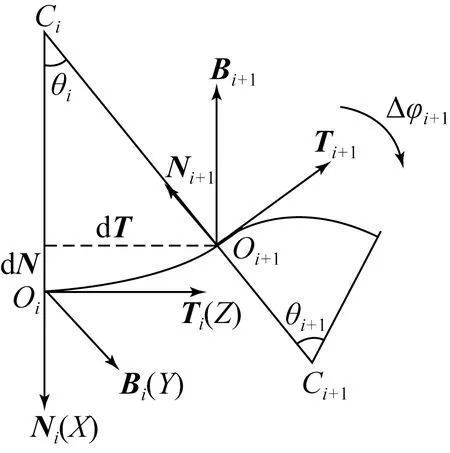
(a)基于Frenet标架的拟合原理图

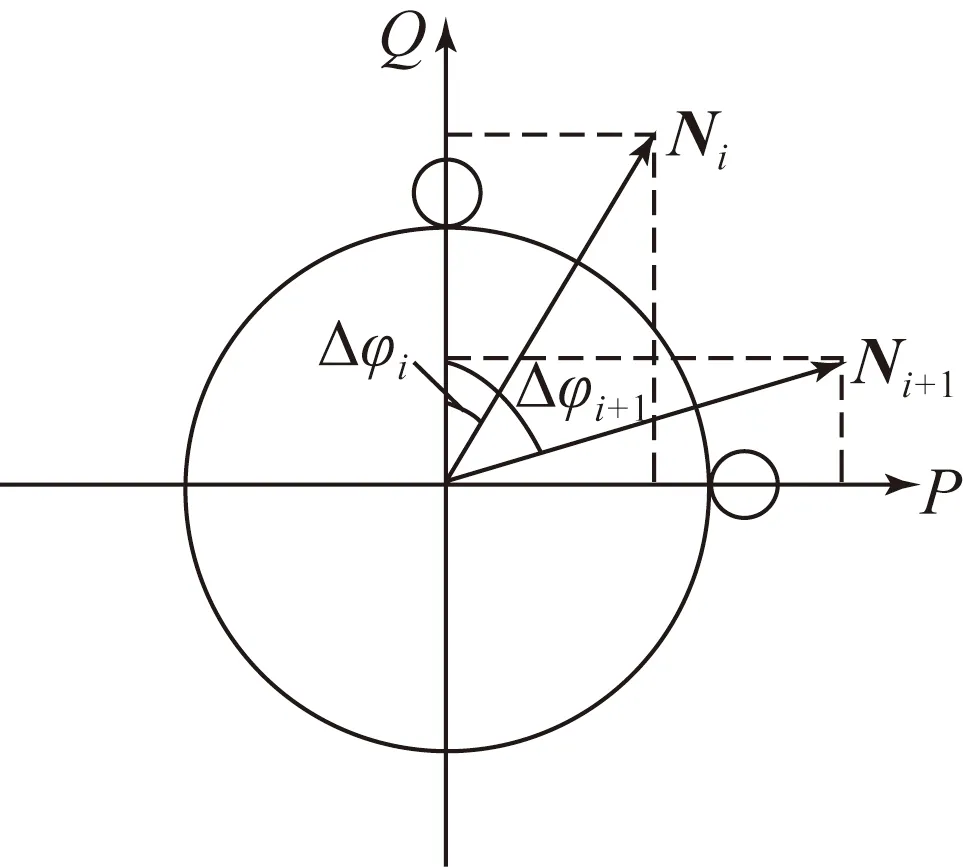
(b)主法线方向绕微段切线方向的旋转变换

(b)Transformation scheme of principle normal rotating around tangent direction of micro-segment

图6基于Frenet标架的坐标点拟合算法

Fig.6Fitting algorithm of coordinate points based on Frenet frame

由此可得求解一个曲线微段的整个过程中运动坐标系的变换矩阵：

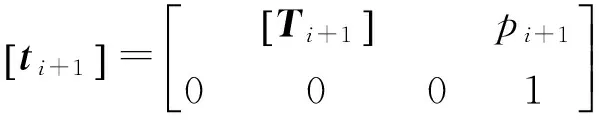
(20)

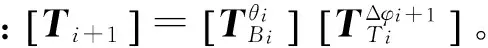
通过此变换矩阵可建立出每一条曲线微段起始点处的运动坐标系，从而求出末端点在运动坐标系中的坐标。将这些坐标全部转化到绝对坐标系x-y-z中，全部连接起来便拟合出一条三维曲线。

相比于曲率方向为坐标轴的坐标点拟合算法，此算法首先需合成垂直方向上的曲率，并将其沿着Frenet标架的N向放置。在计算运动坐标系的旋转及平移变换时，每次只需沿两根轴进行旋转和坐标平移即可。相比前者少了一次旋转变换，减少了计算量，但准确性得到了提升。

4　坐标点拟合算法的验证及对比

4.1二维曲线的拟合对比研究

将封装好的曲线放置于二维毫米方格纸上，并弯曲成图示的圆弧形式，弯曲后的传感器的首尾光栅点的直线距离为600 mm。每一个数据采集点的精确坐标通过毫米方格纸读出，重建数据通过软件读出。图7为实际及拟合的二维曲线。

(a)实验二维曲线实际形状(a)Real shape of 2D curve(b)实验二维曲线拟合形状(b)Fitting shape of 2D curve

Fig.7Shape and fitting graphs of real 2D curve

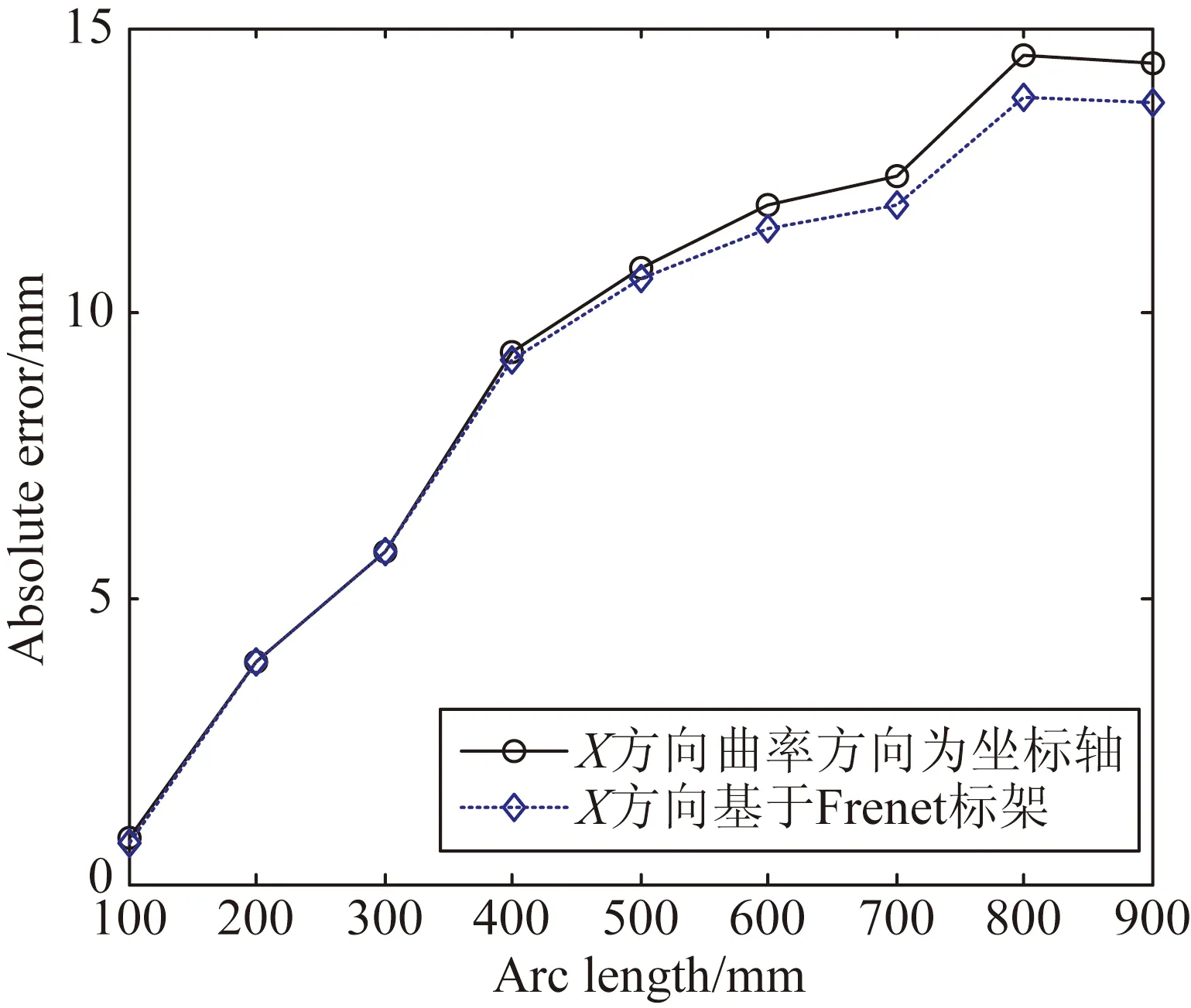
(a)X方向误差对比图

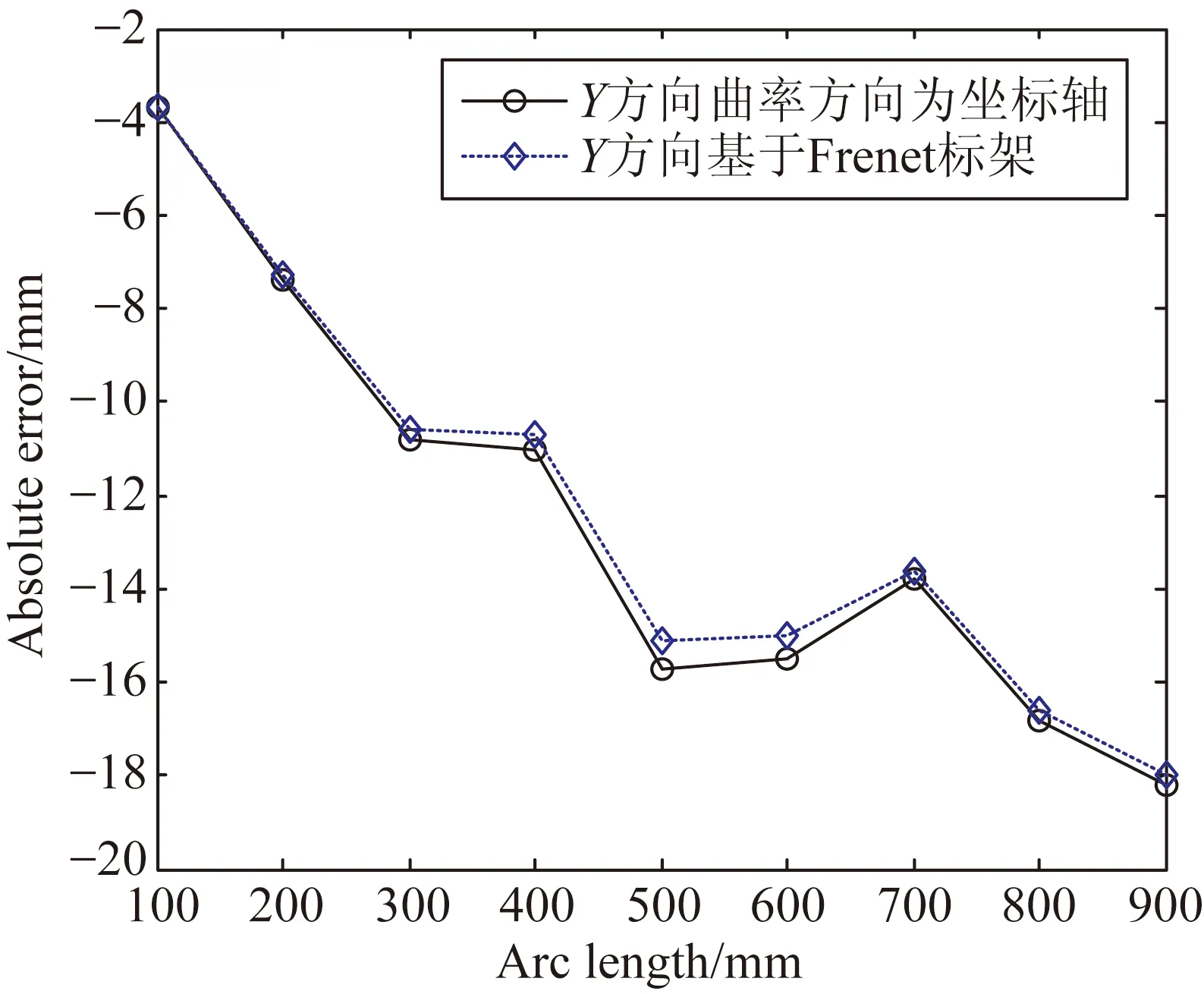
(b)Y方向误差对比图

图8显示了使用两种坐标点拟合法在每一个数据采集点的两个方向上的绝对误差对比图。

表1总结了两种坐标点拟合法在实际曲线的两个方向上和综合的拟合误差平均值以及相应的标准差。(综合误差为两个方向误差的方和根)

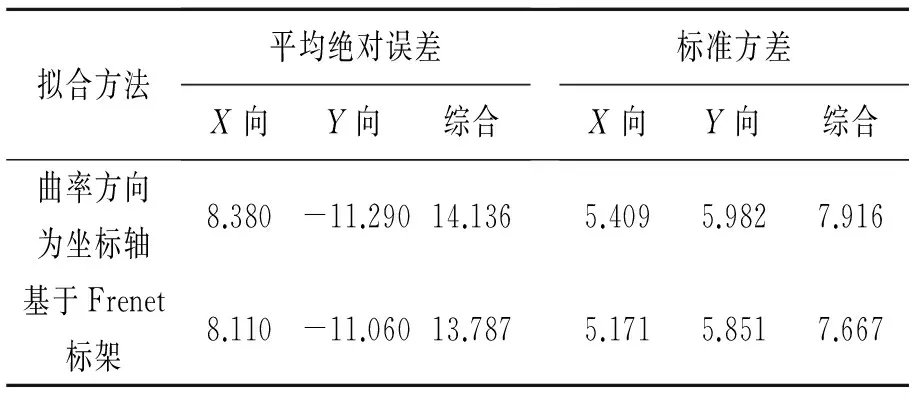
表1　二维曲线的拟合结果对比

由表1可计算出基于Frenet标架的坐标点拟合算法在两个方向上的平均绝对误差减小率(曲率方向为坐标轴拟合法的平均绝对误差和基于Frenet标架拟合法的平均绝对误差的差值与前者的比值)分别为：X向3.2%、Y向2.0%，综合误差减小了2.5%。综合图7和表1可得出以下结论：

(1)在实际曲线的两个方向上使用基于Frenet标架的坐标点拟合方法的误差均不大于曲率方向为坐标轴的坐标点拟合方法的误差；

(2)在综合误差方面，基于Frenet标架的坐标点拟合算法的平均绝对误差比曲率方向为坐标轴的坐标点拟合算法的平均绝对误差低，前者的拟合效果更好；

(3)通过测算得出光栅点的最大应变量为2 355 με，离3 500 με的极限值还有差距。这说明曲线使用基于Frenet标架的坐标点拟合算法至少能够比曲率方向为坐标轴的坐标点拟合算法在单方向上的误差平均减小约2%～3.2%。

4.2三维曲线的拟合对比研究

对于三维实际曲线的验证，本文首先在二维平面图纸上画出倾角为atan(1/9)的直线，再将它围在直径为450 mm的圆柱周围，这样便形成了一条等径螺旋曲线。根据平面倾角和圆柱直径可算出等径螺旋曲线方程，再由每个数据采集点的弧长可确定相应的理论坐标值。测量时将传感器沿着划线部分依次放置，固定后通过软件读取重建数据。图9为实际及拟合的三维曲线。

(a)实验三维曲线实际形状(a)Real shape of 3D curve(b)实验三维曲线拟合形状(b)Fitting shape of 3D curve

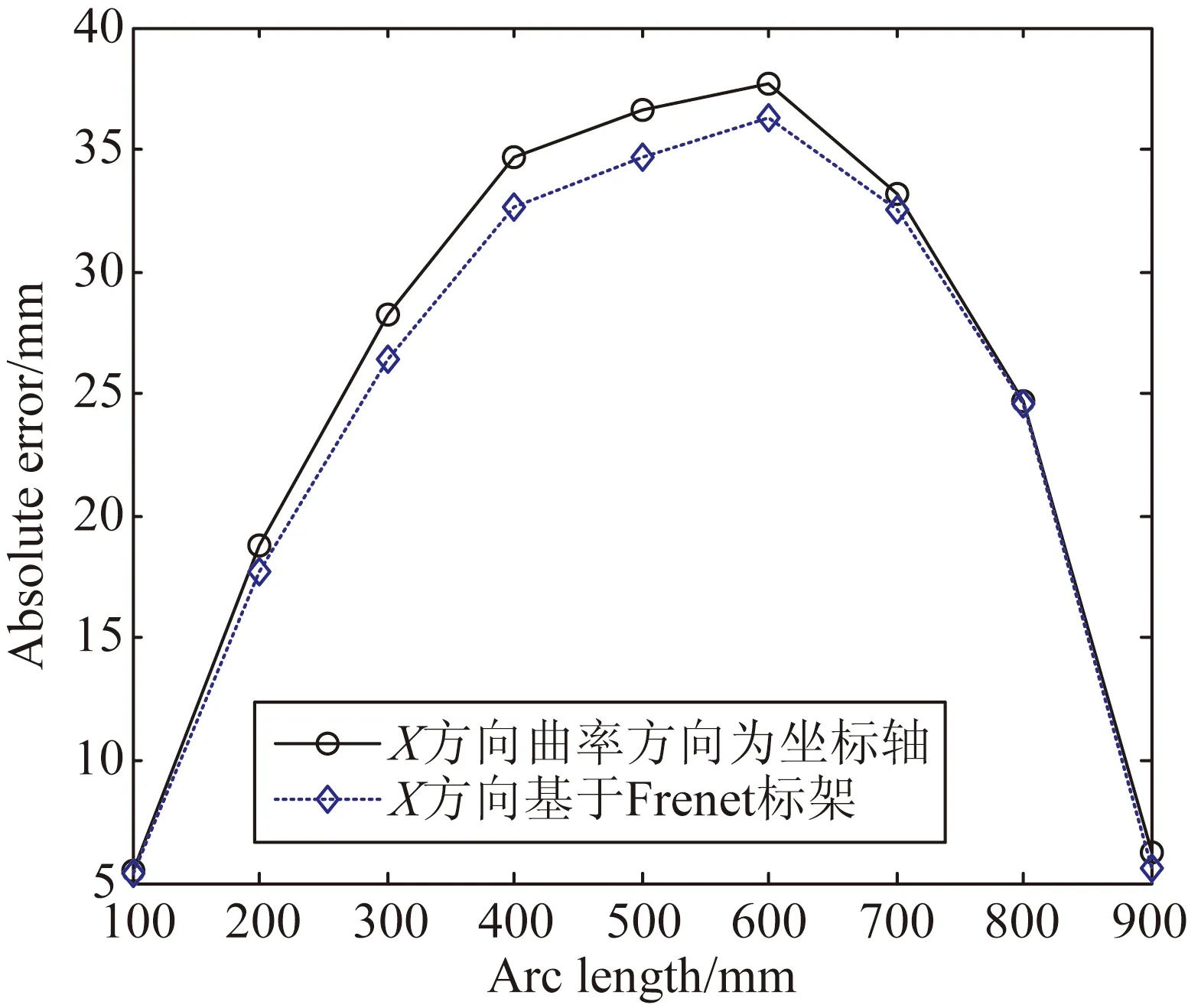
(a)X方向误差对比图

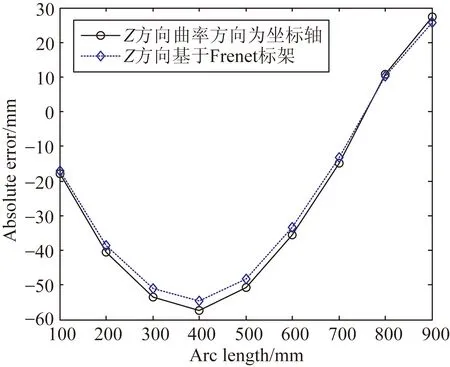
(c)Z方向误差对比图

图10显示了使用两种坐标点拟合法在每一个数据采集点的3个方向上的绝对误差对比图。

表2分别总结了两种坐标点拟合法在实际曲线的3个方向上和综合的拟合误差平均值以及相应的标准差。(综合误差为3个方向误差的方和根)

表2　三维曲线的拟合结果对比

由表2可计算出基于Frenet标架的坐标点拟合算法在3个方向上的平均绝对误差减小率分别为：X向4.3%、Y向3.7%、Z向5.4%，综合误差减少了4.2%。综合图9和表2可得出以下结论：

(1)在实际曲线的3个方向上使用基于Frenet标架的坐标点拟合方法的误差均不大于曲率方向为坐标轴的坐标点拟合方法的误差；

(2)在综合误差方面，基于Frenet标架的坐标拟合算法的平均绝对误差比曲率方向为坐标轴的坐标拟合算法低，说明前者的拟合效果更好；

(3)通过测量计算得出光栅点的最大应变量为3 288 με，接近3 500 με的极限值。这说明传感器在接近弯曲极限的情况下，使用基于Frenet标架的坐标点拟合算法能够比曲率方向为坐标轴的坐标点拟合算法在单方向上的误差平均减小约3.5%～5.5%。

5　结　论

本文以结肠内窥镜在检测过程中的镜体实时显示为背景，将光纤光栅曲线传感器作为研究对象，对比研究了曲率方向为坐标轴以及基于Frenet标架的两种坐标点拟合法。实验结果表明：在基于曲率信息的二维及三维曲线拟合中，使用基于Frenet标架的坐标点拟合算法来代替曲率方向为坐标轴的坐标点拟合算法能够有效提高曲线的重建精度。对于接近光纤光栅应变极限情况下的曲线段而言，使用基于Frenet标架的坐标点拟合算法在单方向上的误差能够比曲率方向为坐标轴的坐标点拟合算法平均减小约3.5%～5.5%。本文研究为提升光纤光栅形状传感系统的精度打下了基础。

另外，相邻采样点之间的微段数量也将影响曲线的重建精度，关于此方面的研究还有待开展，以便进一步提高曲线算法的重建精度。

[1]ELAYAPERUMAL S， PLATA J C， HOLBROOK A B，etal.. Autonomous real-time interventional scan plane control with a 3-D shape-sensing needle[J].IEEETransactionsonMedicalImaging， 2014， 33(11): 2128-2139.

[2]SHI C Y， GIANNAROU S， LEE S L，etal.. Simultaneous catheter and environment modeling for trans-catheter aortic valve implantation[C].IEEE/RSJInternationalConferenceonIntelligentRobotsandSystems(IROS2014)， 2014: 2024-2029.

[3]ARATA J， TERAKAWA S， FUJIMOTO H. Fiber optic force sensor for medical applications within a backbone-shape structure[J].ProcediaCIRP， 2013， 5: 66-69.

[4]钱晋武， 郑庆华， 张伦伟， 等. 渐进式内窥镜形状的感知和重建[J]. 光学 精密工程， 2004， 12(5): 518-524.

QIAN J W， ZHENG Q H， ZHANG L W，etal..Deformation sensing and incremental shape reconstruction for intelligent colonoscope[J].Opt.PrecisionEng.， 2004， 12(5): 518-524. (in Chinese)

[5]YI X H， QIAN J W， ZHANG Y N，etal.. 3-D shape display of intelligent colonoscope based on FBG sensor array and binocular vision[C].IEEE/ICMEInternationalConferenceonComplexMedicalEngineering， 2007: 14-19.

[6]沈林勇， 肖海， 钱晋武， 等. 智能内窥镜的形状重建和可视化方法研究[J]. 仪器仪表学报， 2014， 35(12): 2725-2730.

SHEN L Y， XIAO H， QIAN J W，etal..Shape reconstruction and visualization of intelligent endoscope[J].ChineseJournalofScientificInstrument， 2014， 35(12): 2725-2730. (in Chinese)

[7]余见能， 沈林勇， 张震， 等. 废墟搜救机器人形位检测系统[J]. 上海大学学报：自然科学版， 2011， 17(3)：253-258.YU J N， SHEN L Y， ZHANG ZH，etal..Shape and position detection of search and rescue robot used in ruins[J].JournalofShanghaiUniversity：NaturalScience， 2011， 17(3)：253-258. (in Chinese)

[8]吴家麒， 杨东英， 沈林勇， 等. 基于曲率数据的曲线拟合方法研究[J]. 应用科学学报， 2003， 21(3): 258-262.

WU J Q， YANG D Y， SHEN L Y，etal..Research on the curve-fitting method based on curvature data[J].JournalofAppliedScience， 2003， 21(3): 258-262. (in Chinese)

[9]杨东英， 吴家麒， 钱晋武. 内窥镜镜体形状的三维重建方法研究[J]. 应用科学学报， 2003， 21(4): 406-410.

YANG D Y， WU J Q， QIAN J W. A research on the 3D reconstruction of the shape of the endoscope[J].JournalofAppliedScience， 2003， 21(4): 406-410. (in Chinese)

[10]XIAO H， ZHANG Y N， SHEN L Y，etal.. Three dimensional curve reconstruction based on fiber Bragg grating sensors[C].2015InternationalConferenceonEstimation，DetectionandInformationFusion(ICEDIF)， 2015: 377-382.

[11]钱晋武， 孙流川， 沈林勇， 等. 非开挖地下管线探测中的弯曲变形检测装置研究[J]. 光学 精密工程， 2005， 13(2): 179-184.QIAN J W， SUN L CH， SHEN L Y，etal..On sensing apparatus for bending deformation in trenchless underground pipeline detection[J].Opt.PrecisionEng.， 2005， 13(2): 179-184. (in Chinese)

[12]朱晓锦， 蒋丽娜， 孙冰， 等. 基于B样条拟合的光纤光栅机敏柔性结构形态重构[J]. 光学 精密工程， 2011， 19(7): 1627-1634.

ZHU X J， JIANG L N， SUN B，etal..Shape reconstruction of FBG intelligent flexible structure based on B-spline fitting[J].Opt.PrecisionEng.， 2011， 19(7): 1627-1634. (in Chinese)

[13]ROESTHUIS R J， KEMP M，DOBBELSTEEN J J，etal.. Three-dimensional needle shape reconstruction using an array of fiber Bragg grating sensors[J].IEEE/ASMETransactionsonMechatronics， 2014， 19(4): 1115-1126.

[14]梅向明， 黄敬之. 微分几何[M]. 第四版.北京：高等教育出版社， 2008.

MEI X M， HUANG J ZH.DifferentialGeometry[M]. Forth Edition. Beijing：Higher Education Press， 2008. (in Chinese)

章亚男(1962-)，女，浙江绍兴人，博士，教授，1982年于浙江大学获得学士学位，2011年于上海大学获得博士学位，主要研究方向为数字医疗设备与光电传感技术。E-mail: ynzhang@shu.edu.cn

肖海(1991-)，男，上海人，硕士研究生，2013年、2016年于上海大学分别获得学士、硕士学位，主要研究方向为光纤光栅形状传感技术。E-mail: hai-xiao@163.com

(版权所有未经许可不得转载)

Coordinate point fitting in FBG curve reconstruction algorithm

ZHANG Ya-nan*， XIAO Hai， SHEN Lin-yong

(SchoolofMechatronicEngineeringandautomation，ShanghaiUniversity，Shanghai200072，China)*Correspondingauthor，E-mail：ynzhang@shu.edu.cn

To detect the shape of a Fiber Bragg Grating(FBG) sensor in a colon， a coordinate fitting method based on Frenet frame was proposed to improve the precision of the FBG curve reconstruction algorithm. Firstly， four FBGs perpendicular to each other were clinged to one Shape Memory Alloys(SMA) substrate. Hence， one FBG curve sensor with a diameter of 3 mm and a length of 900 mm was formed. Then， this sensor was put on a millimeter-square graph paper and a cylinder respectively to accomplish the reconstruction of 2D and 3D curves. Furthermore， every reconstructed value of data collection points was read from the curve reconstruction software and reconstruction errors were acquired by the contrast between the reconstructed values and the standard values read from the coordinate paper. Finally， the merit degree between two fitting methods was obtained. Experimental results show that the proposed coordinate fitting method based on Frenet frame effectively improves the reconstruction accuracy. When the FBG achieves their ultimate strain， the proposed fitting method can reduce the average error by 3.5%—5.5% at single direction， which lays a foundation for the precision upgrading of the FBG curve sensing system.

fiber Bragg grating; curve reconstruction algorithm; coordinate fitting; Frenet frame; shape detection

2016-03-04；

2016-05-19.

国家科技支撑计划资助项目(No.2013BAK03B01-02)

1004-924X(2016)09-2149-09

TN253

A

10.3788/OPE.20162409.2149