Robust Resilient Guaranteed Cost Control for Singular Impulsive Switched Systems with Time-varying Delay*

王庆芝，宗广灯

(曲阜师范大学工程院，山东日照 276826)



Robust Resilient Guaranteed Cost Control for Singular Impulsive Switched Systems with Time-varying Delay*

王庆芝，宗广灯

(曲阜师范大学工程院，山东日照 276826)

This paper focuses on the problem of robust resilient guaranteed cost control for a class of singular impulsive switched systems with time-varying delay.Based on the multiple Lyapunov functional technique,some sufficient criteria,ensuring the regularity,causality,and asymptotic stability,are obtained initially for the nominal and unforced systems.Then the resilient controller is designed such that the corresponding closed-loop system,for all admissible uncertainties,is regular,causal and asymptotically stable, and the cost function does not exceed a cost upper bound.Further,a minimization approach of the largest singular value of matrices and a convex optimization method are introduced to seek the optimal robust resilient guaranteed cost controller.All the conditions are cast into the form of linear matrix inequalities (LMIs) through ingenious processing.Finally,two examples are presented to illustrate the less conservativeness and the effectiveness of the proposed results.

singular switched systems，impulsive switched systems，resilient guaranteed cost control，multiple Lyapunov technique，linear matrix inequalities (LMIs)

0 Introduction

Switched systems have attracted considerable attention in recent decades[1-7]which include a series of continuous-time or discrete-time subsystems and a switching rule that orchestrates the switching between subsystems.They can be found in various real-world systems such as transportation systems[8-9],electric power systems[10],communication networks[11-12],and chemical processes[13].However,singular phenomena often exist in practical processes modeled by switching systems such as robotics,economics,chemistry and power systems.We call this kind of systems as singular switched systems.The past decades have witnessed considerable research on analysis and synthesis of singular switched systems[14-15].In addition,impulses often take place in various applications modeled by switching systems,which makes it more intricate to analyze the property of impulsive switched systems.Recently,some theoretical results on impulsive switched systems are reported in literatures,respectively[16-21].

In actually physical processes,due to some physical restriction such as resistance errors,A/D or D/A conversion,finite word length in digital systems and rounding off errors in numerical computation,it is impossible to implement controller precisely,and it is important to take the controller gain perturbations into account during the designing process of the controller.On the other hand,the relatively small fluctuation of controller parameters may lead to the performance degradation or even instability.The two aspects above inspire us to design a controller that should be able to tolerate some levels of controller parameter perturbations.This kind of controllers are usually called as “resilient controllers”.Therefore,it is extremely imperative to design a resilient controller,and at the same time, some techniques and approaches solving this problem have been proposed.In [22],the problem of non-fragile hybrid guaranteed cost control is addressed for a class of uncertain switched linear systems.An observer-based resilient controller is designed in [23] for singular time-delay systems.Up to now,just little attention has been paid to design a resilient guaranteed cost controller for singular impulsive switched systems with time-varying delay,which stimulates the authors’ research interests.

Here,we mainly study the robust resilient guaranteed cost control problem for a class of singular impulsive switched systems with time-varying delay.The outstanding contributions lie in several aspects:Firstly,we consider the uncertainty,impulse,singularity and time delay in switched systems at the same time,which throw out the greater challenge for the authors;Secondly,for the singular impulsive switched systems with time-varying delay,the derived conclusions can apply to various systems such as singular switched systems,impulsive switched systems,and singular impulsive systems,which fully demonstrates the less conservativeness and the broader applicability;Thirdly,uncertainties exist not only in the system structure but also in the resilient controller,which make it more difficult to simplify and solve inequalities;Fourthly,we introduce a minimization approach of the largest singular value of matrices and a convex optimization method in this paper to seek the optimal robust resilient guaranteed cost controller;Finally,all the conditions are cast into linear matrix inequalities(LMIs),and two examples are provided to illustrate the effectiveness of the proposed results.

Notations Throughout this paper,T denotes the transpose.Rnrepresents the n-dimensional Euclidean space.Z+is a positive integer set,C stands for complex domain.Matrix P>0(P≥0) means that P is positive definite (positive semi-definite),and I is identity matrix with appropriate dimensions.* stands for the symmetric part in a block symmetric matrix.

1 Problem formulation and preliminaries

Consider the following singular impulsive

switched system with time-varying delay

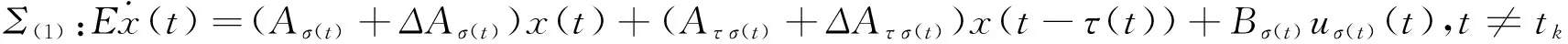
Δx(t)=(Cσ(t)+ΔCσ(t))x(t),t=tk,

x(t)=φ(t),t∈[-τm,0],

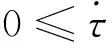
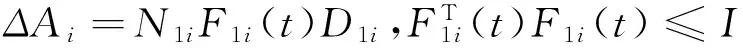
(1)

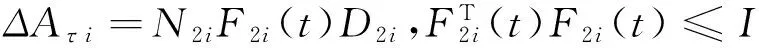
(2)

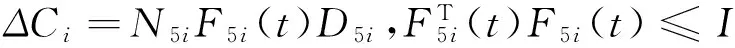
(3)

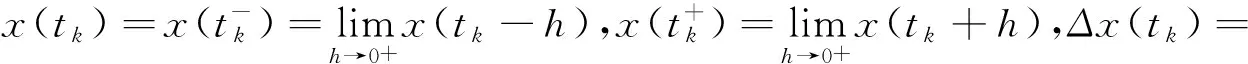
Associated with system Σ(1),the cost function is given by

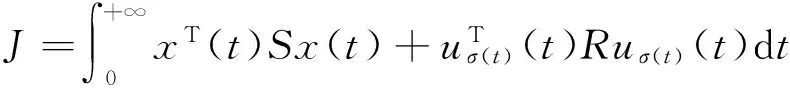
(4)

where S and R are positive definite weighted matrices.

For system Σ(1),a resilient controller

uσ(t)(t)=(Kσ(t)+ΔKσ(t))x(t),

(5)

is considered,where Ki,i∈M is a controller gain to be designed,and ΔKi,i∈M represents a additive controller gain variation which has the following form

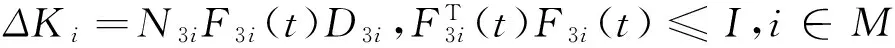
(6)

where N3iand D3iare known real constant matrices,and F3i(t) describes the uncertainty of the controller gain.

Definition 1[15]Consider the pair (E,Aσ(t)).

1.For a given i∈M,the pair (E,Ai) is said to be regular if det(sE-Ai)≠0,s∈C.

2.For a given i∈M,the pair (E,Ai) is said to be causal if it is regular and deg(det(sE-Ai))=rank(E).

3.The pair (E,Aσ(t)) is said to be regular and causal if every pair (E,Ai) is regular and causal,i∈M.

Definition 2[15]The system Σ(1)with ΔAi=0,ΔAτ i=0,ui(t)=0,i∈M is said to be regular and causal if the pair (E,Aσ(t)) is regular and causal.

Remark 1 The existence and uniqueness of the solutions of systems Σ(1)with ΔAi=0,ΔAτ i=0,ui(t)=0 for each i∈M,can be ensured by regularity and causality.

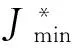
The main object of this paper is to construct a switching signal,design a robust resilient guaranteed cost controller and give an upper bound of the cost function for systems Σ(1).

Lemma 1[24]Let Y=YT,H,E and F be real matrices of appropriate dimensions with FTF≤I.The following statements are equivalent

a.Y+HFE+ETFTHT<0,

Lemma 2[25]For matrix Q≥0, if there is a zero element qion the main diagonal line of Q, then the column and row which qilies on are both zero.

2 Main results

2.1 Stability analysis

In this section,we initially establish stability conditions for the following system Σ(2).

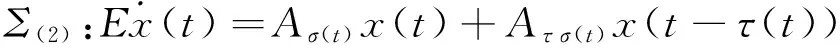
t≠tk,

Δx(t)=Cσ(t)x(t),t=tk,

x(t)=φ(t),t∈[-τm,0].

Theorem 1 Consider system Σ(2).If,for any i∈M, there exist constants βij≥0(j∈M), matrices Qi>0,Xi≥0,Zi>0,Pi,Yisuch that

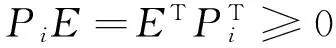
(7)

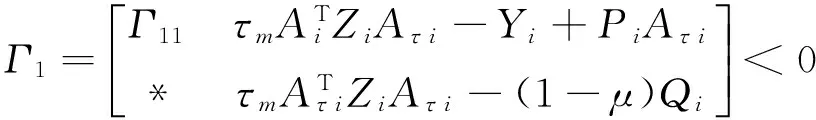
(8)

(I+Cj)TPiE(I+Cj)-PjE≤0,i≠j,j∈M,

(9)

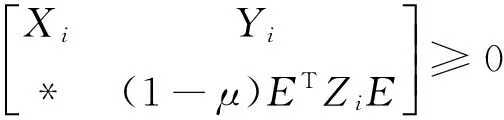
(10)

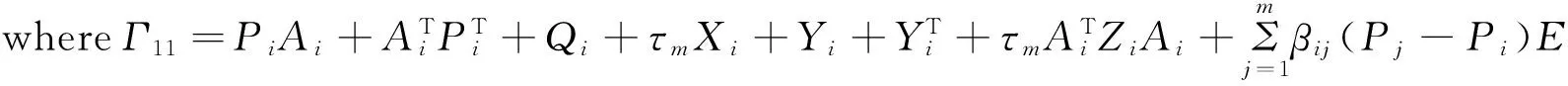
then the system Σ(2)is regular,causal and asymptotically stable under a state-dependent switching signal

σ(t)=argmin{xT(t)PiEx(t),i∈M}.

(11)

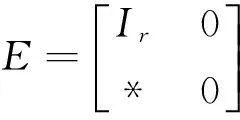
Vσ(t)(t)=xT(t)Pσ(t)Ex(t)+

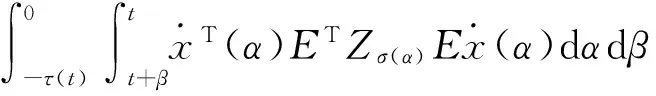
and design the switching signal (11).

When t∈(tk,tk+1],suppose that the i-th subsystem is activated.Then one obtains

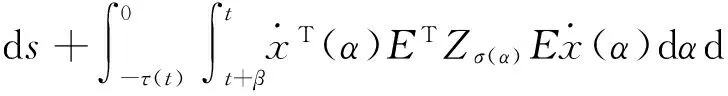
(12)

From (11) and the condition βij≥0,we get

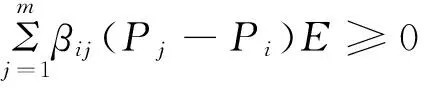
(13)

In the following,we firstly prove that system Σ(2)is regular and causal.

Corresponding to the blocks of matrix E,one denotes

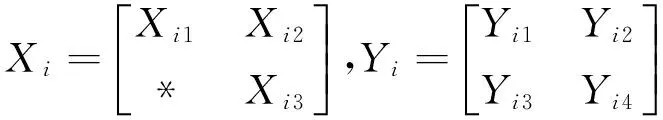
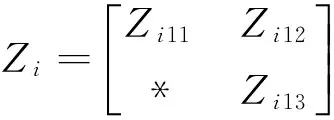
(14)

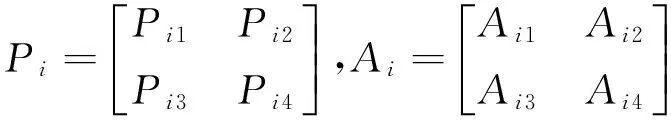
Substituting (14) into (10),we obtain

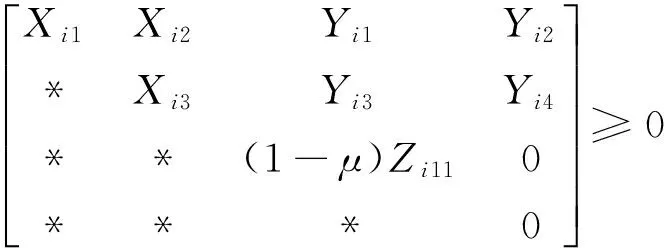
which implies from Lemma 2 that

(15)

From (7),there holds

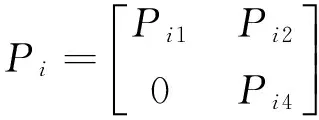
(16)

From (8),we have

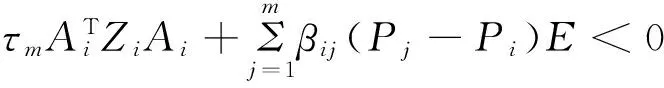
(17)

Bearing (13) and Qi>0,Xi≤0,Zi>0,τm>0 in mind,one gets from (17)

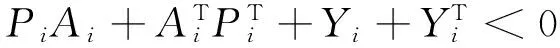
(18)

Subsequently,we will focus on our attention to asymptotical stability analysis.

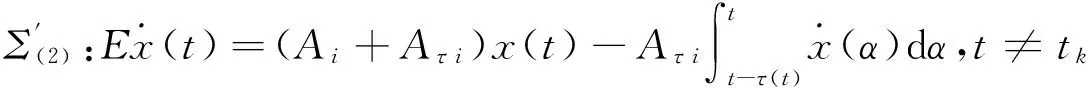
Δx(t)=Cσ(t)x(t),t=tk,

x(t)=φ(t),t∈[-τm,0].

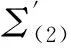
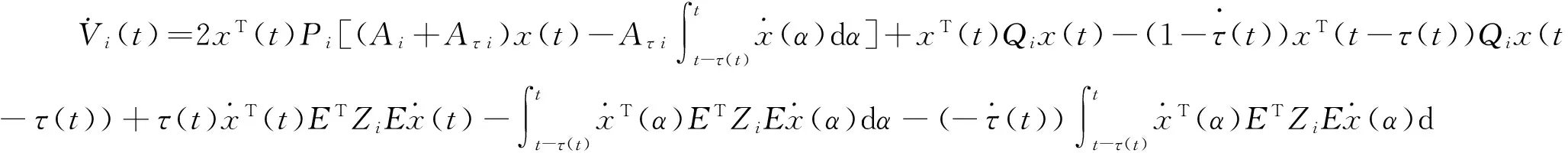
(19)

From (10),it is easy to derive

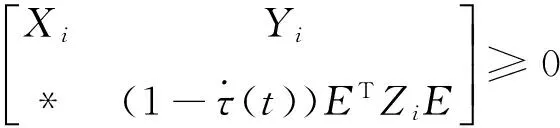
which implies

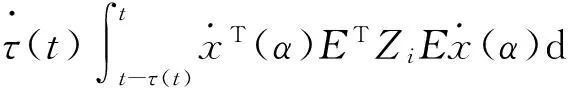
(20)

Substituting (20) into (19) gives

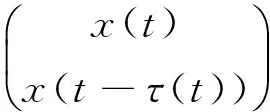
(21)

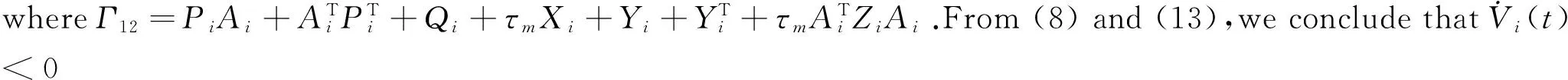
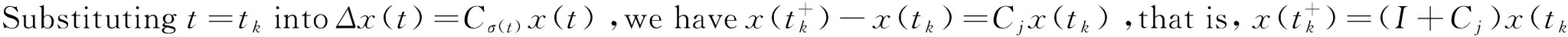
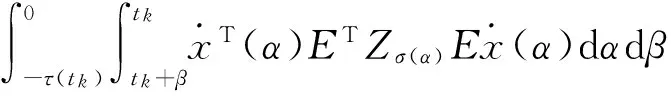
Vj(tk)=xT(tk)PjEx(tk)+

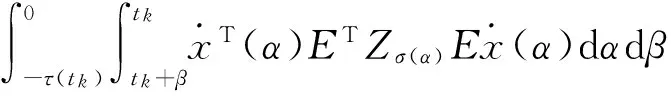
Cj)-PjE]x(tk).

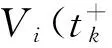
Remark 2 For the nominal and unforced form of the singular impulsive switched system with time-varying delay,this theorem designs the state-dependent switching signal,under which the given system is regular,causal,and asymptotically stable based on the multiple Lyapunov functional technique.Further,it should be observed that this result can also apply to various systems such as singular switched systems,impulsive switched systems and singular impulsive systems.For impulsive switched systems and singular impulsive systems,the following corollaries state the related conclusions,which can fully demonstrate the universality and practicability of the theorem.

Corollary 1 Consider the following impulsive switched system with time delay

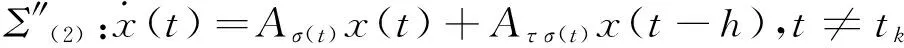
Δx(t)=Cσ(t)x(t),t=tk,

x(t)=φ(t),t∈[-h,0].

If,for any i∈M,there exist constants βij≥0(j∈M),matrices Qi>0,Pi>0 such that

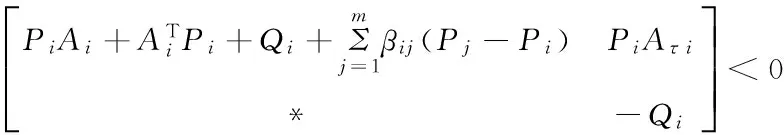
(22)

(I+Cj)TPi(I+Cj)-Pj≤0,i≠j,j∈M,

then the system Σ″(2)is regular,causal and asymptotically stable under a state-dependent switching signal σ(t)=argmin{xT(t)Pix(t),i∈M}.

Remark 3 Theorem 2 in paper [18] requires that the energy function decreases on the whole space Rn,that is,every subsystem is stable on the whole space Rn,while this corollary just requires that the energy function decreases on the corresponding area Ωi,which can stand out the merit of the result proposed in the paper.

Corollary 2 Consider the following singular time-varying delay system

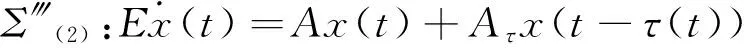
x(t)=φ(t),t∈[-τm,0].

If there exist matrices Q>0,X≥0,Z>0,P and Y such that

PE=ETPT≥0,

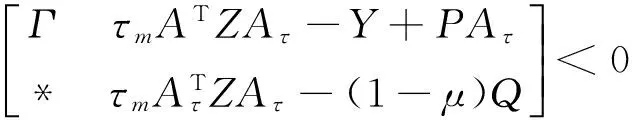
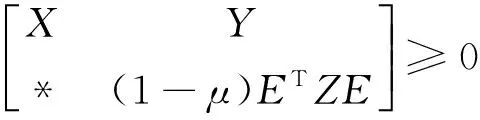
with Γ=PA+ATPT+Q+τmX+Y+YT+τmATZA,then systems Σ‴(2)is regular,causal and asymptotically stable.

Remark 4 Lemma 2 in literature [23] studies the constant time delay while this corollary presents the corresponding results for the time-varying delay.

Corollary 3 Consider system Σ(2).If,for any i∈M,there exist constants βij≤0(j∈M),matrices Qi>0,Xi≥0,Zi>0,Pi,Yisatisfying (7),(8),(9),(10),then system Σ(2)is regular,causal and asymptotically stable under a switching signal

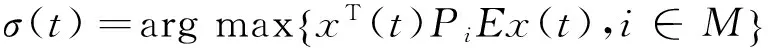
(23)

Remark 5 When βij≤0,this corollary designs a new state-dependent switching signal (23),which differs from Theorem 1.In a word,this corollary,together with Theorem 1,shows two different cases.

2.2 Performance analysis

Based on Theorem 1,we are now in the position to provide the sufficient conditions on the existence of a robust resilient guaranteed cost controller for system Σ(1).

Theroem 2 Consider system Σ(1)with the cost function (4).If,for i∈M,there exist scalars βij≥0(j∈M),matrices Qi>0,Xi≥0,Zi>0,Pi,Yisatisfying (7),(10) and

Γ2=

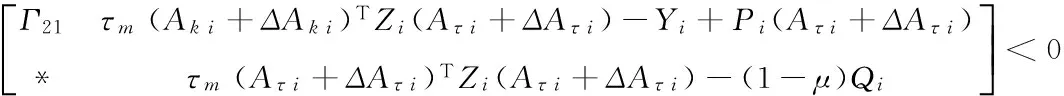
(24)

(I+Cj+ΔCj)TPiE(I+Cj+ΔCj)-PjE≤0,i≠j,j∈M,

(25)

where

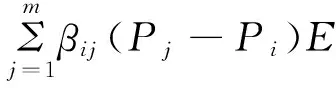
Ak i=Ai+BiKi,ΔAk i=ΔAi+BiΔKi,

and a state-dependent switching signal (11),then controller (5) is a robust resilient guaranteed cost controller for system Σ(1)with the performance upper bound

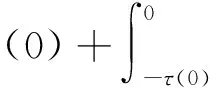
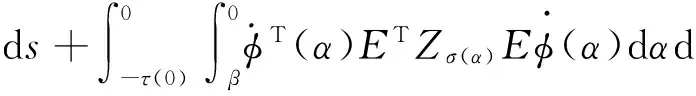
Proof When t∈(tk,tk+1],assume that the i-th subsystem is activated.Applying the controller (5) to systems Σ(1)results in the following closed-loop system

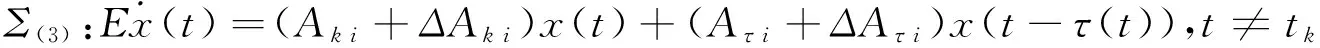
Δx(t)=(Cj+ΔCj)x(t),t=tk,

x(t)=φ(t),t∈[-τm,0].

Based on Theorem 1 and R>0,S>0,it is easy to obtain that the closed-loop system Σ(3)is also regular,causal and asymptotically stable by replacing Ai,Aτ i,Cjwith Ak i+ΔAk i,Aτ i+ΔAτ i,Cj+ΔCj.In the next,we shall prove that there exists a positive scalar J*such that the value of the cost function (4) satisfies J≤J*.Similar to the proof of Theorem 1,when t∈(tk,tk+1],one has

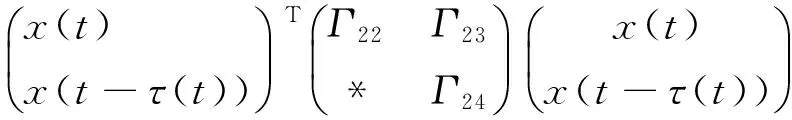
where

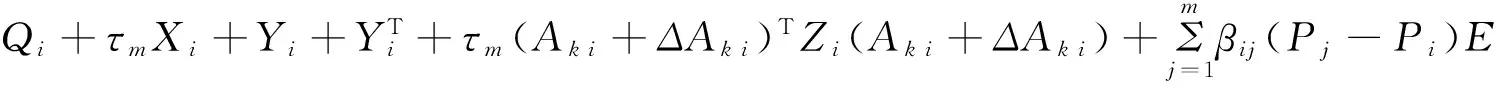
Γ23=τm(Ak i+ΔAk i)TZi(Aτ i+ΔAτ i)-Yi+Pi(Aτ i+ΔAτ i),

Γ24=τm(Aτ i+ΔAτ i)TZi(Aτ i+ΔAτ i)-(1-μ)Qi.

From (24),we derive

(26)

which gives rise to

Vσ(tρ+1)(tρ+1)]≤Vσ(0)(0)=J*.

Therefore,by Definition 3,controller (5) is a robust resilient guaranteed cost controller for system Σ(1)with the performance upper bound J*.The proof is completed.

Remark 6 Based on the Theorem 1,this theorem further analyzes the performance of the singular impulsive switched system with time-varying delay.It is necessary to point out that the controller designed in Theorem 2 is not only a guaranteed cost controller but also a resilient controller.In addition,there exist uncertainties in the system structure,which,together with uncertainties in resilient controller,make it more difficult to simplify inequalities.The corresponding process will be stated in detail.

Remark 7 The paper [23] designs a robust resilient guaranteed cost controller for the uncertain singular time-delay system,but the main results in [23] fail to work when impulsive phenomena or switching behaviors occur.On the contrast, this theorem is feasible for the case that impulsive phenomena and switching behaviors take place at the same time.Obviously,Theorem 1 in literature [23] is the special case of this theorem,which shows that this conclusion has the broader application and less conservativeness.

Remark 8 It should be observed that the paper [18] ignores uncertainties of impulses.Here,it is more meaningful to add the uncertain term ΔCσ(t)to the system matrix,which to some extent can reflect some uncertainties of impulsive phenomena.Besides,compared with the paper [18],the more complex systems are considered and the more information in Lyapunov functional are added in this theorem.

Corollary 4 Consider system Σ(1)with the cost function (4).If,for i∈M,there exist scalars βij≤0(j∈M),matrices Qi>0,Xi≥0,Zi>0,Pi,Yisatisfying (7),(10),(24),(25),and a state-dependent switching signal satisfying (23),then controller (5) is a robust resilient guaranteed cost controller for system Σ(1)with the performance upper bound J*in the form of (26).

2.3 The robust resilient guaranteed cost controller design

In Theorem 2,uncertain terms ΔAi,ΔAτ i,ΔKi,ΔCjexist in conditions,which makes it impossible to solve inequalities.Therefore,how to remove uncertain terms is the key to overcome this problem.Here,by the LMIs technique,the feasible conditions solving a robust resilient guaranteed cost controller for systems Σ(1)are presented in Theorem 3.

Theorem 3 Consider system Σ(1)with the cost function (4).If,for any i∈M,the following conditions hold

a.there exist scalars βij≥0(j∈M),λi>0,i>0,ρj>0,matrices Qi>0,Xi≥0, Zi>0,Pi,Yi,Gisatisfying (7),(10) and

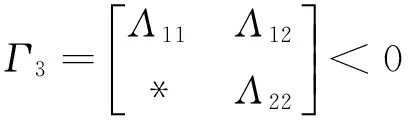
(27)

i≠j,j∈M,

(28)

where

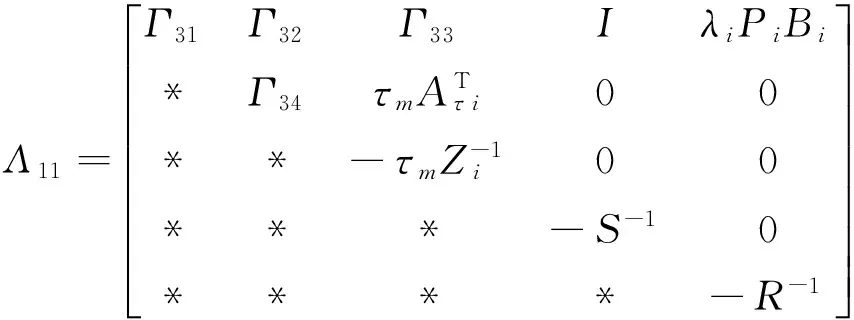
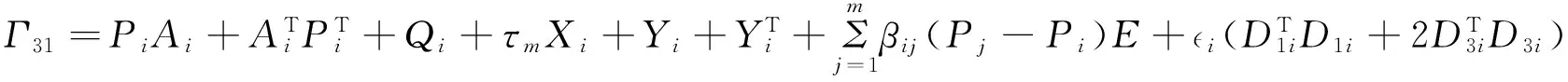
Γ32=PiAτ i-Yi,

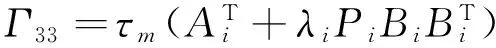
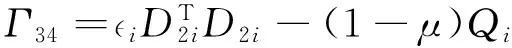
Λ12=

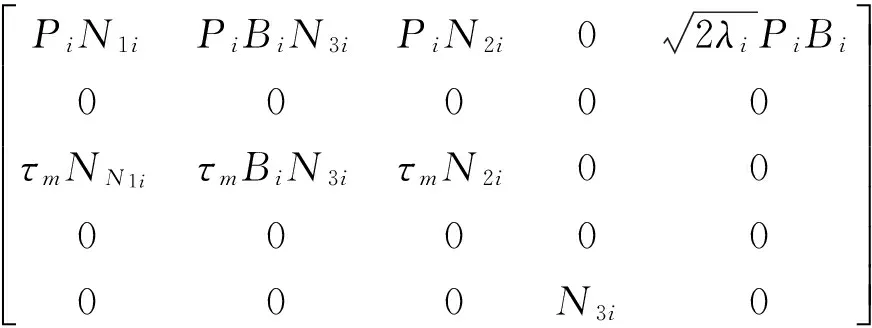
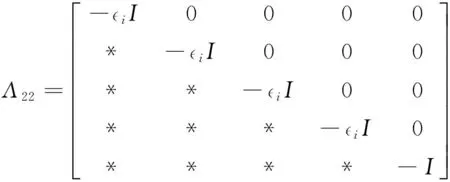
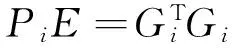
b.there exists a state-dependent switching signal satisfying (11),then controller (5) is a robust resilient guaranteed cost controller for system Σ(1).Here,the controller gain is

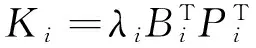
(29)

and the performance upper bound J*can be given in the form of (26).

Proof Using (27),(29),and Schur complement lemma,we obtain thatΓ3<0 is equivalent to

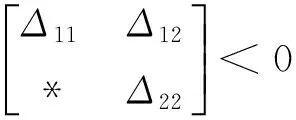
(30)

where

Δ11=

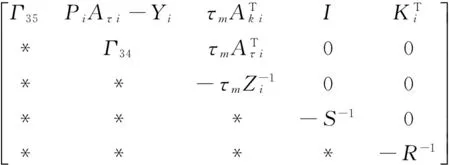
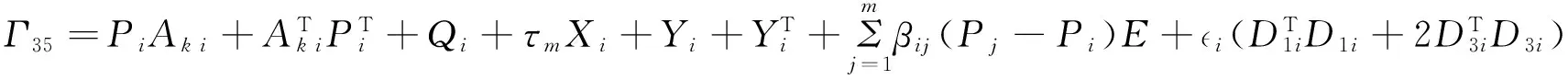
Ak i=Ai+BiKi,

Δ12=

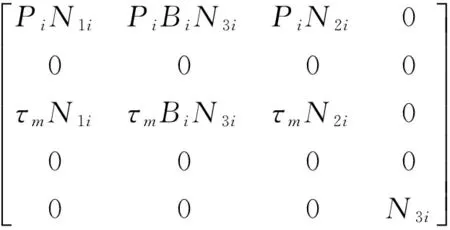
Δ22=

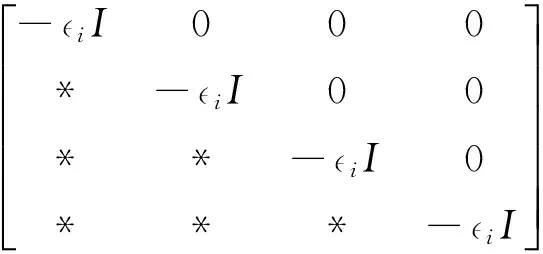
From (30),we can derive

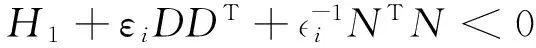
(31)

where

H1=

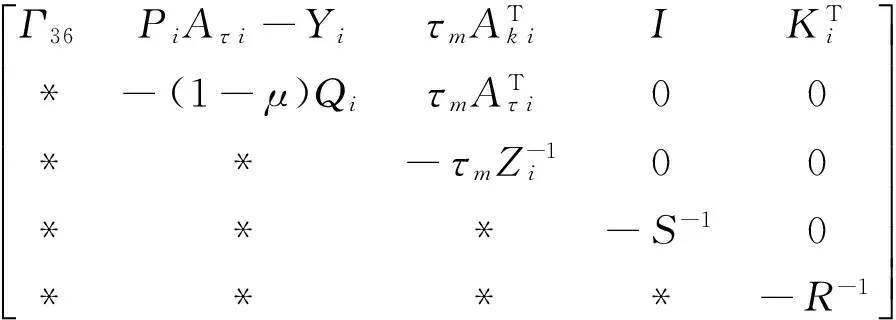
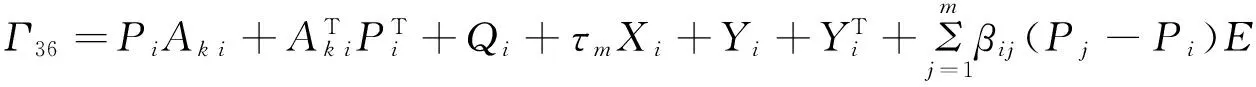
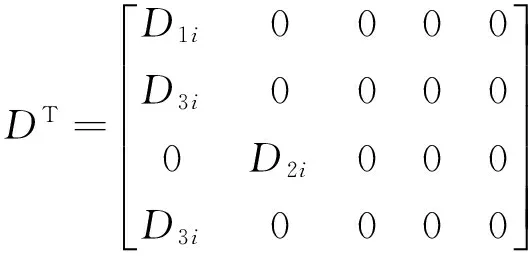
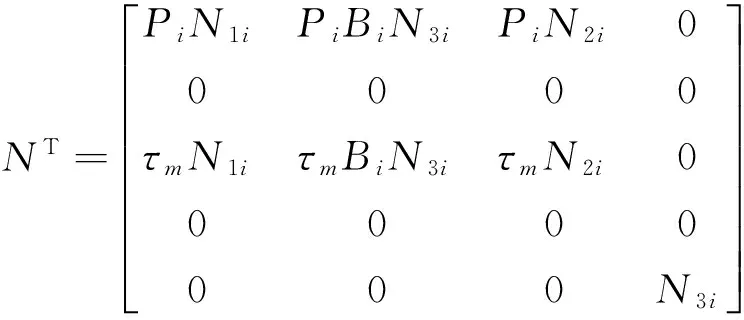
Define

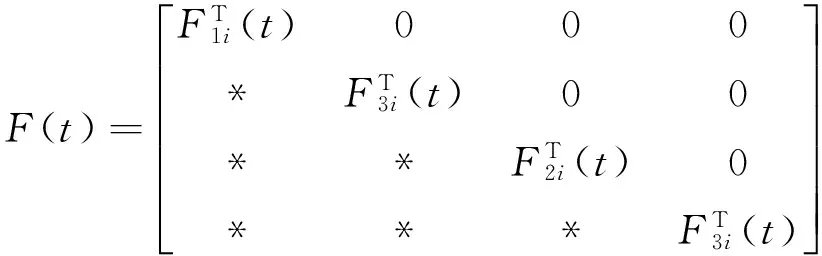
After some manipulations,by Lemma 1,we get from (1),(2),(6)

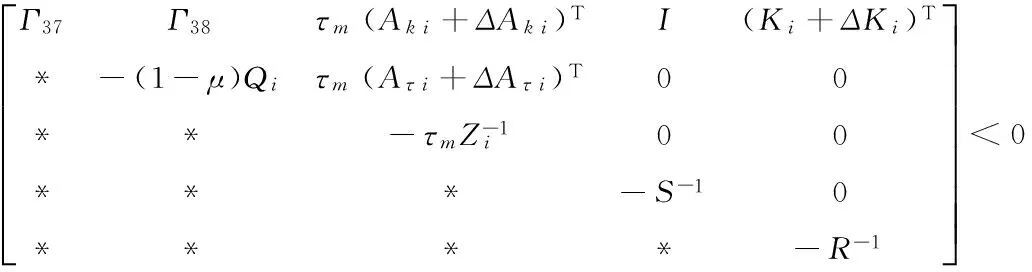
(32)

Pi(Aτ i+ΔAτ i)-Yi. Obviously,we can see that (32) is equivalent to (24).From (28),by Schur complement lemma,one has

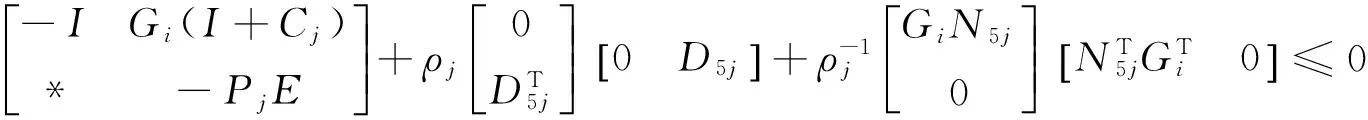
(33)

By Lemma 1,(3) and (33),we get

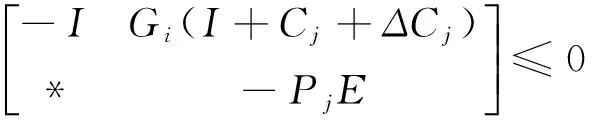
(34)

Remark 9 It is easy to see that various techniques are utilized to simplify inequalities of Theorem 2.Eventually,uncertain terms are successfully removed from conditions.Meanwhile,all the conditions are cast into LMIs for the given scalars βij,λi,which can be solved by the LMIs toolbox.

Remark 10 We state briefly the solving sequence of inequalities of Theorem 3.

Step 1 Calculate the Pi,Qi,Xi,Zi,Yiby (7),(10) and (27).

Step 3 Verify the condition (28),and solve the controller gain by (29).

Corollary 5 Consider system Σ(1)with the cost function (4).If,for any i∈M,the following conditions hold

a.there exist scalars βij≤0(j∈M),λi>0,i>0,ρj>0,matrices Qi>0,Xi≥0,Zi>0,Pi,Yi,Gisatisfying (7),(10),(27),(28),

b.there exists a state-dependent switching signal satisfying (23),then controller (5) is a robust resilient guaranteed cost controller for system Σ(1).Here,the controller gain is (29),and a performance upper bound J*can be given in the form of (26).

2.4 The optimal robust resilient guaranteed cost controller design

Theorem 3 factually presents a set of parameter representations of guaranteed cost controllers.From the expression of J*,the upper bound of the performance not only depends on the selection of guaranteed cost controllers but also matrices Qi,Zi.Therefore,it is imperative to optimize the values of matrices in order to achieve the minimal guaranteed cost of the corresponding closed-loop system.

Theorem 4 For system Σ(1)with ΔCσ(t)=0,and the cost function (4),if the following optimization problem Ωopt

minβij,λi,i,Pi,Qi,Zi,Xi,YiC1αi+C2βi+C3γis.t.

(a)(7),(9),(10),(27),

(b)βij≥0(j∈M),

(c)λi>0,i>0,

(35)

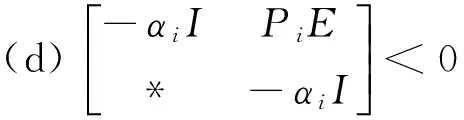
(36)

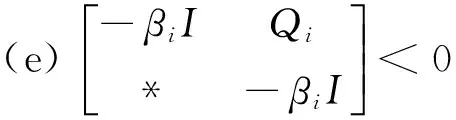
(37)

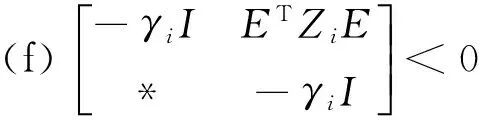
(38)

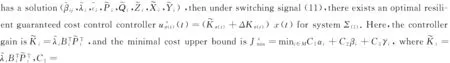
σmax(PiE)C1,

Therefore,the minimization of C1αi+C2βi+C3γiimplies the minimization of the guaranteed cost J*.The optimal solution of problem Ωoptcan be derived from the convexity of the objective function and constraint conditions.This completes the proof.

Remark 11 In order to obtain the optimal robust resilient guaranteed cost controller,a minimization approach of the largest singular value of matrices and a convex optimization method are introduced,which play an important role in the proof.In addition,Theorem 3 provides a feasible solution of solving a robust resilient guaranteed cost controller while this theorem further gives a optimal robust resilient guaranteed cost controller.To some extent,this theorem improves the conclusion of Theorem 3.

3 Numerical examples

Example 1 Consider the impulsive switched systems Σ″(2)with parameters given below

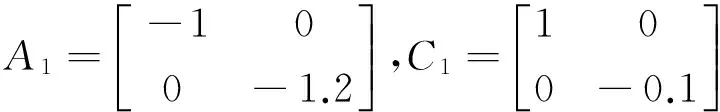
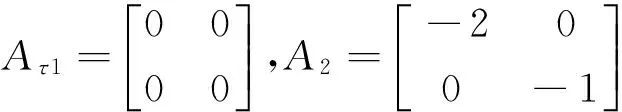
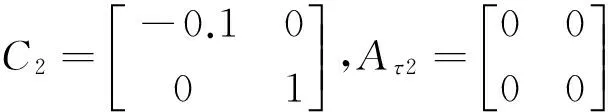
For the given system,the linear matrix inequalities have not a feasible solution by Theorem 2 in [18].Therefore,we are unable to judge the stability of the above system and Theorem 2 in [18] fails to work.However,Corollary 1 in this paper can be worked well to check the stability of the given system.Choosing β12=-0.2,β21=-0.1,we can see that the nonlinear matrix inequality (22) becomes the linear matrix inequality which can be solved by LMIs toolbox as following

Under the switching signal σ(t)=argmin{xT(t)Pix(t),i∈{1,2}},the given system is asymptotically stable from Fig.1,which can verify the feasibility of Corollary 1.In conclusion,both the theoretical analysis in Remark 3 and simulation result can show the fact that Corollary 1 has the wider application and the less conservativeness than the result in [18].

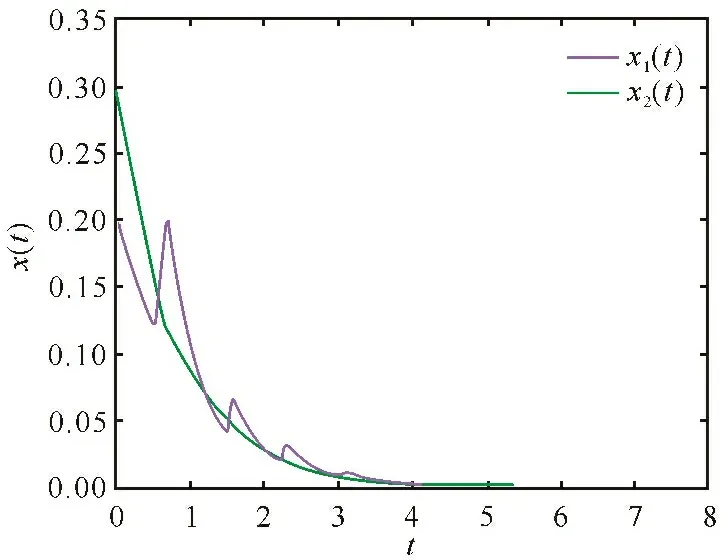
Fig.1 The state trajectory x(t) of the given system

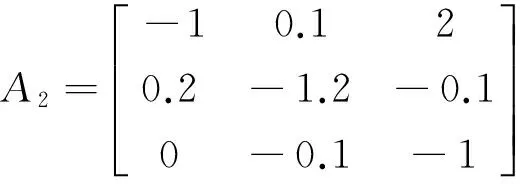
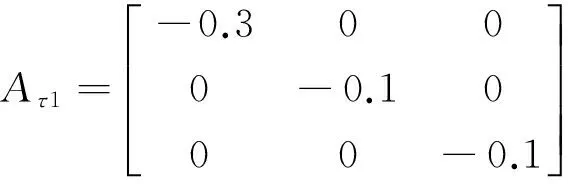
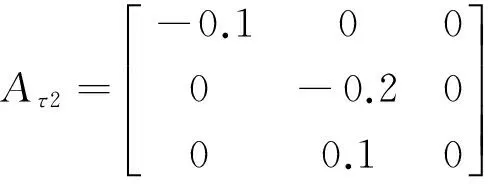
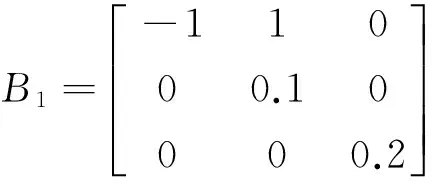
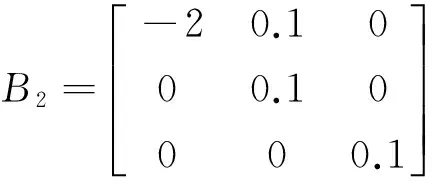
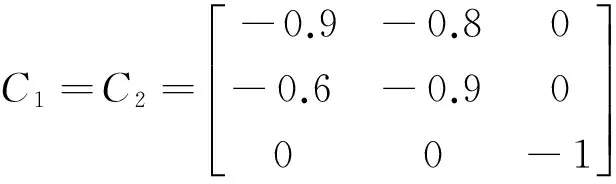
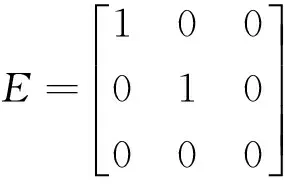
S=R=I,

N1i=N2i=N3i=D1i=D2i=D3i=0.1I,N5i=

D5i=0,i=1,2,

F1i=F2i=F3i=F5i=0.1sin(t)I,i=1,2,

τ(t)=0.1sint.

Choose τm=1,μ=0.1,λ1=λ2=0.01,and give the initial function φ(t)=[1 t 0]T.

By Theorem 3,we can obtain

a robust resilient guaranteed cost controller uσ(t)(t)=(Kσ(t)+ΔKσ(t))x(t) with

and a performance upper bound J*=8.677 0.The above results derived from Theorem 3 just present a feasible solution.In the following,we aim at seeking the optimal controller and the optimal performance upper bound of systems Σ(1)by Theorem 4.By solving optimization problem Ωopt,one gets

The switching signal is designed by

(39)

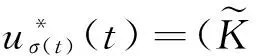
From Fig.2,under the switching signal (39),the closed-loop system is asymptotically stable,which can illustrate the correctness of Theorem 4.

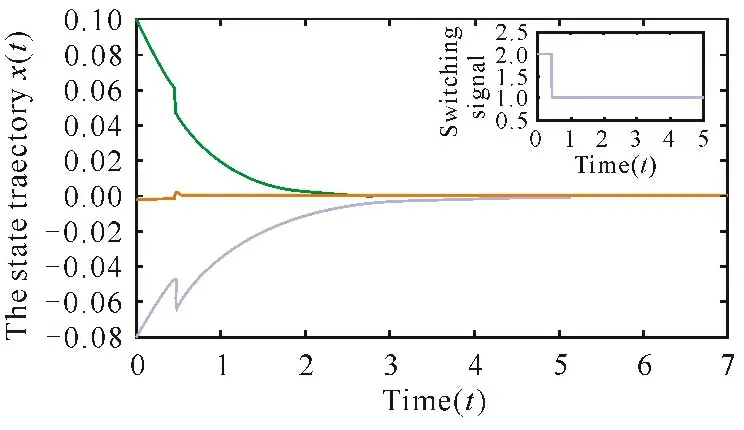
Fig.2 The state trajectory x(t) of the closed-loop system

4 Conclusions

In this paper,we have investigated the problem of the robust resilient guaranteed cost control for the uncertain impulsive switched singular system with time-varying delay.A robust resilient guaranteed cost controller and a state-dependent switching signal have been established,which guarantee that the closed-loop system is regular,causal,asymptotically stable,and satisfies a cost upper bound.Further,a minimization approach and a convex optimization method have been presented to seek the optimal robust resilient guaranteed cost controller.For the sake of the computation,all the conditions have been cast into LMIs,which can be easily solved by the LMIs toolbox.Finally,two examples have been provided to show the effectiveness of the main conclusions.

[1] HESPANHA J P,MORSE A S.Stability of switched systems with average dwell-time[C]//Proceedings of the 38th IEEE Conference on Decision and Control Arizona,USA:IEEE,1999:2655-2660.DOI:10.1109/CDC.1999.831330.

[2] LIBERZON D,MORSE A S.Basic problems in stability and design of switched systems[J].IEEE Control Systems Magazine,1999,19(5):59-70.

[3] WANG R,ZHAO J.Non-fragile hybrid guaranteed cost control for a class of uncertain switched linear systems[J].Journal of Control Theory and Applications,2006,4(1):32-37.DOI:10.1007/s11768-006-5144-x.

[4] WU Z G,SHI P,SU H Y, et al.Asynchronous l2-lfiltering for discrete-time stochastic markov jump systems with randomly occurred sensor nonlinearities[J].Automatica,2014,50(1):180-186.

[5] YANG H,JIANG B,COCQUEMPOT V.A survey of results and perspectives on stabilization of switched nonlinear systems with unstable modes[J].Nonlinear Analysis:Hybrid systems,2014,13:45-60.

[6] ZHANG H B,XIE D H,ZHANG H Y,et al.Stability analysis for discrete-time switched systems with unstable subsystems by a mode-dependent average dwell time approach[J].ISA Transactions,2014,53(4):1081-1086.

[7] ZONG G D,HOU L L,WU Y Q.Robust l2-lguaranteed cost filtering for uncertain discrete-time switched system with mode-dependent time-varying delays[J].Circuits,Systems,and Signal Processing,2011,30(1):17-33.DOI:10.1007/s00034-010-9204-6.

[8] VARAIYA P.Smart cars on smart roads:Problems of control[J].IEEE Transactions on Automatic Control,1993,38(2):195-207.

[9] 王亦兵,韩曾晋,罗赞文.智能运输系统初探[J].控制与决策,1997,12(S1):403-407.

WANG Y B,HAN Z J,LUO Z W.An Opening study of intelligent transportation systems[J].Control and Decision,1997,12(S1):403-407.

[10] QIN S Y,SONG Y H.The theory of hybrid control

systems and its application perspective in electric power systems[C]//Proceedings of the 2001 International Conferences on Info-tech and Info-net. Beijing:IEEE,2001,4:85-94.DOI:10.1109/ICII.2001.983729.

[11] HU S S,ZHU Q X.Stochastic optimal control and analysis of stability of networked control systems with long delay[J].Automatica,2003,39(11):1877-1884.

[12] WU Z G,SHI P,SU H Y,et al.Stochastic synchronization of markovian jump neural networks with time-varying delay using sampled data[J].IEEE Transactions on Cybernetics,2013,43(6):1796-1806.DOI:10.1109/TSMCB.2012.2230441.

[13] LENNARTSON B,TITTUS M,EGARDT B,et al.Hybrid systems in process control[J].IEEE Control Systems Magazine,1996,16(5):45-56.DOI:10.1109/37.537208.

[14] LIN J X,FEI S M,WU Q.Reliable H∞filtering for discrete-time switched singular systems with time-varying delay[J].Circuits,System,and Signal Processing,2012,31(3):1191-1214.DOI:10.1007/s00034-011-9361-2.

[15] MA S P,ZHANG C H,WU Z.Delay-dependent stability and H∞control for uncertain discrete switched singular systems with time-delay[J].Applied Mathematics and Computation,2008,206(1):413-424.

[16] LIU X,ZHANG S M,DING X Y.Robust exponential stability of nonlinear impulsive switched systems with time-varying delays[J].Nonlinear Analysis:Modeling and Control,2012,17(2):210-222.

[17] 毛北行,慕小武,卜春霞.不确定时滞脉冲切换系统的保性能控制[J].郑州大学学报：理学版,2010,42(3):7-10.

MAO B X,MU X W,BU C X.Guaranteed cost control problems for a class of impulsive switched system with time delay and uncertain parameters[J].J Zhengzhou Univ:Nat Sci Ed,2010,42(3):7-10.

[18] XU H L,TEO K L,LIU X Z.Robust stability analysis of guaranteed cost control for impulsive switched systems[J].IEEE Transactions on Systems,Man,and Cybernetics,Part B:Cybernetics,2008,38(5):1419-1422.

[19] XU H L,LIU X Z,TEO K L.A LMI approach to stability analysis and synthesis of impulsive switched systems with time delays[J].Nonlinear Analysis:Hybrid Systems,2008,2(1):38-50.

[20] YANG C D,ZHU W.Stability analysis of impulsive

switched systems with time delays[J].Mathematical and Computer Modelling,2009,50(7/8):1188-1194.

[21] ZONG G D,XU S Y,WU Y Q.Robust H∞stabilization for uncertain switched impulsive control systems with state delay:An LMI approach[J].Nonlinear Analysis:Hybrid Systems,2008,2(4):1287-1300.

[22] WANG R,ZHAO J.Non-fragile hybrid guaranteed

cost control for a class of uncertain switched linear systems[J].Journal of Control Theory and Applications,2006,4(1):32-37.

[23] LI L,JIA Y.Observer-based resilient l2-l∞control for singular time-delay systems[J].IET Control Theory & Applications,2009,3(10):1351-1362.DOI:10.1049/iet-cta.2008.0361.

[24] XIE L H.Output feedback H∞control of systems with

parameter uncertainty[J].International Journal of Control,1996,63(4):741-750.

[25] ZHANG F Z.Matrix Theory:Basic Results and Techniques[M].New York:Springer-Verlag,1999.

(责任编辑：米慧芝)

2016-05-11

王庆芝(1988-),女,主要从事切换系统、鲁棒控制研究。

http://www.cnki.net/kcms/detail/45.1206.G3.20160913.0948.014.html

时变时滞奇异脉冲切换系统的鲁棒弹性保成本控制

WANG Qingzhi,ZONG Guangdeng**

(School of Engineering，Qufu Normal University，Rizhao，Shandong，276826，China)

针对一类具有时变时滞的奇异脉冲切换系统，研究鲁棒弹性保成本控制问题.首先，基于多Lyapunov泛函技术，建立标称自由系统具有正则性、因果性及渐近稳定性的充分条件.然后，给出一个弹性保性能控制器的设计方案，该方案能保证对所有容许的不确定性，闭环系统是正则的、因果的和渐近稳定的，且成本函数不超过某个上界.并进一步运用矩阵最大奇异值的最小化方法和凸优化方法，求解最优鲁棒弹性保成本控制器.所有的充分条件均巧妙地表示为线性矩阵不等式形式.最后，运用两个仿真实例验证本研究方法较少的保守性和有效性.

奇异切换系统 脉冲切换系统 弹性保成本控制 多Lyapunov 技术 线性矩阵不等式

TP273

A

1005-9164(2016)04-0354-12

修回日期：2016-08-03

*国家自然科学基金项目(61273123,61374004,61304059),新世纪优秀人才支持计划项目(NCET-13-0878),山东省高校优秀科研创新团队计划项目和山东省泰山学者计划项目资助。

**通讯作者:宗广灯(1976-),男,教授,主要从事网络控制,切换系统和鲁棒控制研究,E-mail:lovelyletian@gmail.com,zonggdeng@126.com。

网络优先数字出版时间：2016-09-13 【DOI】10.13656/j.cnki.gxkx.20160913.007

广西科学Guangxi Sciences 2016,23(4):354～365