缓冲结构对静电驱动微桥动力学特性的影响

张琪昌，陈 涛，王 炜

（天津大学机械工程学院天津市非线性动力学与混沌控制重点实验室，天津 300072）

缓冲结构对静电驱动微桥动力学特性的影响

张琪昌，陈 涛，王 炜

（天津大学机械工程学院天津市非线性动力学与混沌控制重点实验室，天津 300072）

可动部件是微机电系统（MEMS）工作的关键，微桥作为主要的可动部件，其动力学特性引起了研究人员的广泛关注．即使是设计精准的微桥结构，也会因为残余应力而不可避免地改变初始形态，设计缓冲结构是减少残余应力影响的重要方法．基于欧拉-伯努利梁理论建立的微桥动力学模型，采用多尺度方法进行摄动分析，探讨初始形态、基板与极板间隙、直流偏置电压和交流激励电压幅值对系统共振频率和幅频响应的影响规律．结果表明：初始挠形、直流偏置电压和交流激励电压都具有软化效应，使共振频率漂移到较小的数值范围，且随着拱高增加或基板与极板间隙减小，软化效应增强，随着微拱曲率增大，软化效应减弱；缓冲结构可以削弱软化效应，缓冲结构的褶皱数量在2个以上时削弱效果变化不大，双侧翘曲缓冲结构削弱软化效应的能力强于单侧翘曲缓冲结构．

微桥；初始形态；缓冲结构；多尺度法

随着科学技术日新月异式的快速发展和人类日益增长的生活需求，微机电系统凭借微、精、准的优点，在很多领域得到广泛应用．对应用最广泛的静电驱动微桥结构的研究，主要集中在静态和动力学特性分析上．Rhoads等［1］通过理论和实验分析发现，不同参数下的微系统存在着迥异的非线性动力学特性，影响因素主要是静电力和系统几何结构．Hornstein等［2］通过研究原子力显微镜的超谐响应和亚谐响应，证实了微系统在静电力影响下存在差异明显的非线性软硬特性．多晶硅微桥作为微系统的主要可动部件，其动力学特性决定着微系统的工作性能．由于加工工艺的限制，设计精准的微桥结构内部也会存在残余应力［3-4］，形成微拱［5-6］．

通常采用缓冲结构［5］和去应力退火处理消除残余应力［6］对微桥机械性能的影响．Krylov等［7］研究了直流偏置电压和交流激励电压对双侧加压悬臂微拱系统的动力学特性的影响，发现了微拱共振频率、稳态幅值与直流偏置电压和交流电压的幅值及频率间的关系．Krylov等［8-9］以静电驱动微拱结构为研究对象，着重考察了系统几何参数对其自身动力学特性的影响，发现主要影响因素是微拱厚度、微拱高度和微拱与极板间距．Younis等［10］研究了不同尺度下拱高对微拱的振型和非线性行为的影响，同时仔细讨论了激励电压对系统工作特性的影响，发现交流电压幅值的大小影响微拱的非线性共振频率，直流偏置电压和交流电压幅值的大小共同决定微拱的稳态振幅．Ruzziconi等［11-12］通过理论分析研究了不同参数下微拱的多种非线性行为，发现系统工作时非共振与共振同时存在并在两者之间转换，结论与实验分析所得现象相吻合，同时还得到了可靠的微拱结构多尺度降阶模型．Ruzziconi等［13］还利用理论分析和数值模拟等方法研究了微拱的非线性行为和动态完整性，结果表明通过设计适当的偏置电压可以保证系统的动态完整性．

以上研究人员通过分析微拱系统几何非线性和机械非线性，得到了微拱几何参数、系统结构参数和静电力设计参数对微拱动力学特性的影响，同时提出了一系列的改进方案来提高微系统的工作性能，极大地促进了微机电系统的发展［7-14］．虽然残余应力引起的机械非线性问题得以解决，但初始形态改变所引起的几何非线性问题依然存在．笔者通过研究微桥的动力学特性，探讨初始形态、基板与极板间隙、直流偏置电压和交流激励电压幅值对系统共振频率和幅频响应的影响规律．

1　缓冲结构

“牺牲层腐蚀”技术是指在基底表面淀积微结构，腐蚀掉牺牲层，保留衬底材料的制作方法．腐蚀掉牺牲层后，衬底受到残余应力的作用，将会翘曲形成微拱，如图1所示．

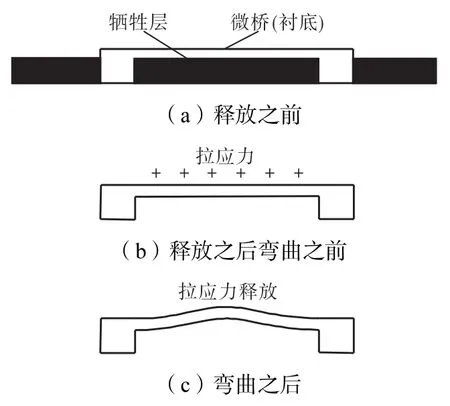
图1 微拱形成过程Fig.1 Forming process of micro-arches

通常选择设计缓冲结构减少拱起对微桥工作性能的影响，一般选取褶皱作为缓冲结构的形式．设微桥的形函数为

式中：b0为最大初始挠度，即拱高；l为梁长；n、p为形函数控制参数．研究对象如图2所示，分别为微拱、单侧褶皱微桥和双侧褶皱微桥．

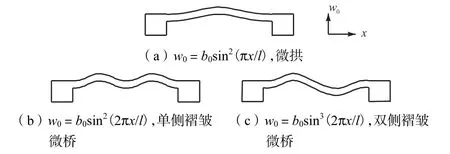
图2 3种典型的含缺陷微桥Fig.2 Three kinds of typically defective micro-bridges

2　运动方程与振动响应方程

微桥的动力学模型如图3所示，采取对称放置直流偏置电压既可以有效降低直流偏置电压对微桥结构的影响，还有利于微桥动力学特性的发挥．微桥的材料参数和几何参数如表1所示．

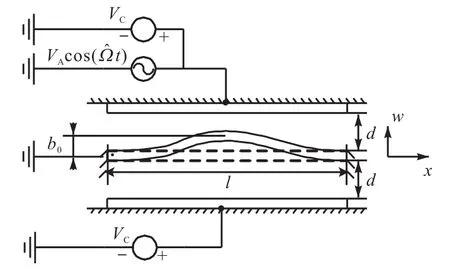
图3 两侧静电驱动双端固支微桥模型Fig.3Model of double lateral electrostatically actuated clamped-clamped micro-bridges

表1 微桥的材料参数和几何参数Tab.1 Material parameters and geometric parameters of micro-bridges

微桥的动力学方程为

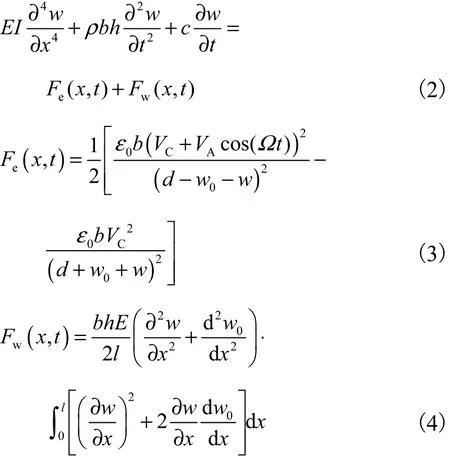
式中：E、ρ、c分别为多晶硅弹性模量、密度、阻尼系数；b、h、I分别为微桥的宽度、厚度、惯性矩；w为微桥的垂直位移；Fe、Fw分别为静电力和几何非线性力；0ε为空气介电常数；d为板间隙；VC、VA分别为极板上加载的直流电压和交流电压.

引入无量纲量

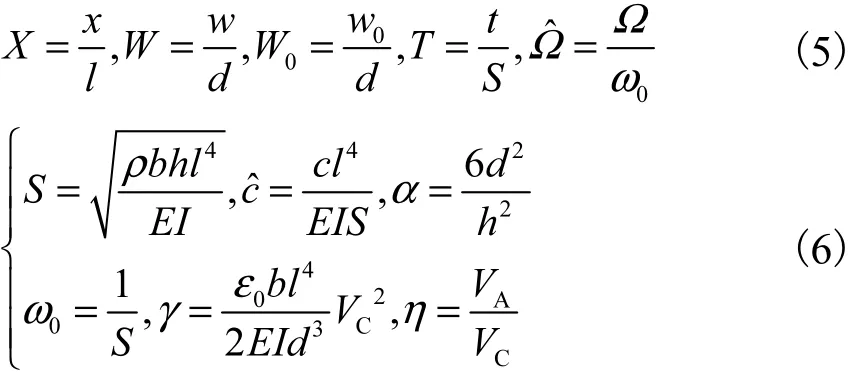
微桥做小幅振动，舍去高阶位移项，得无量纲式

微桥的振型函数采取一阶近似［14］，即

经伽辽金离散、泰勒展开，平衡位置坐标变换得到系统动力学方程的无量纲式为

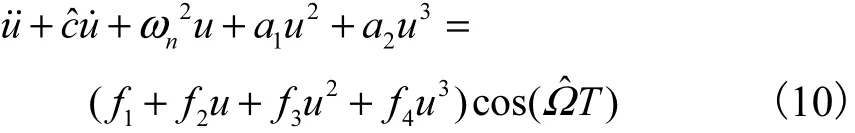
假设静电驱动微拱系统作为弱非线性系统，系统参数用小参数变量ε表示，得

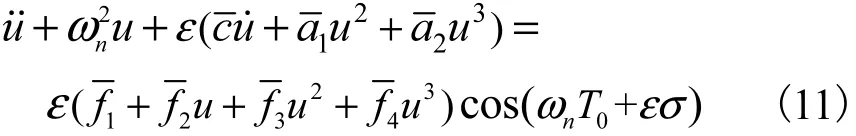
利用多尺度法对式（11）进行摄动分析，得微桥的振动响应方程为

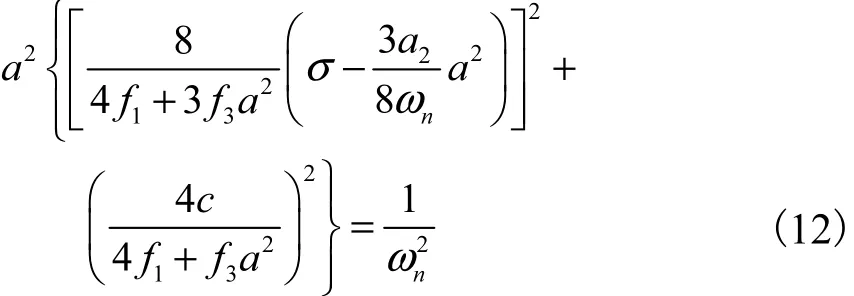
计算分析式（12）可以得到微桥幅频响应与控制参数间的关系．

将双侧模型退化为单侧模型，取如下参数：l= 400，μm，b=50，μm，h=1，μm，间隙为2.2µm，直流偏置电压VC=1V，交流激励电压VA=50 mV ，得到的微拱幅频关系与Ouakad等［15］测得的实验结果基本一致，见图4．

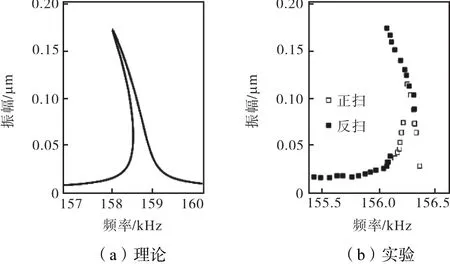
图4 单侧静电驱动微拱的理论与实验幅频关系Fig.4Theoretical and experimental amplitude-frequency relations of single lateral electrostatically actuated micro-arches

3　理论分析

微梁的初始形态显著影响微器件的工作性能，如改变微谐振器在指定工作范围内的敏感度，引起高频开关出现弛豫现象等．本节通过理论分析探究不同初始形态的微桥的动力学特性，以及拱高、直流偏置电压、交流激励电压幅值和基板与极板间隙对动力学特性的影响．

3.1初始形态对静电吸合效应的影响

静态吸合指在极板上施加驱动电压后，弹性基板受静电力作用弯曲变形，施加电压达到某一临界值，基板与极板发生接触，此时系统的固有频率为零．取控制参数：板间隙10µm，拱高2.5µm，得到不同初始形态的微桥固有频率与直流偏置电压的关系，如图5所示，b0=0表示理想微桥，p=1、n=2表示微拱，p=2、n=2表示单侧褶皱微桥，p=2、n=3表示双侧褶皱微桥．相对于理想微桥，初始形态改变导致吸合电压缩减，特别是微拱的吸合电压缩减超过1/3，而双侧褶皱微桥缩减低于5%．初始形态改变引起的稳定性问题不容忽视，缓冲结构可以提高微器件的工作稳定性和精确度．

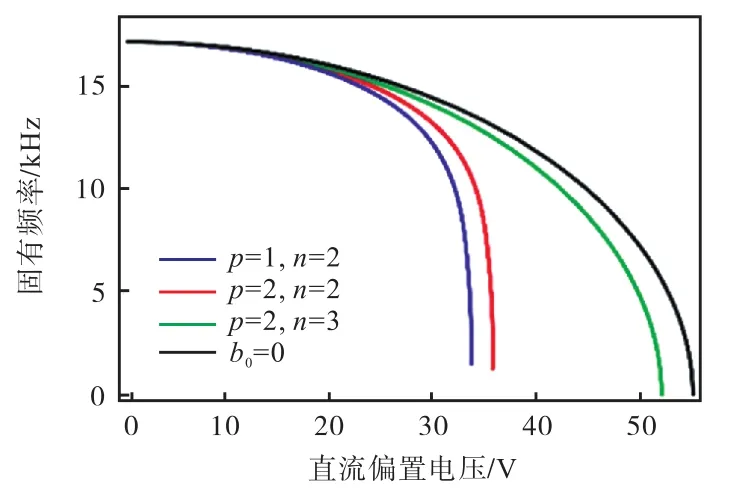
图5 微桥固有频率与直流偏置电压的关系Fig.5 Relationship between natural frequencies of microbridges and DC bias voltage

3.2初始形态对共振频率的影响

共振频率作为表征微梁动力学性能的重要参数．本节取控制参数：板间隙10µm，直流偏置电压VC=25 V ，拱高b0=2.5µm ，探讨初始形态对共振频率的影响，如图6所示．可以看出，初始挠形使微桥的共振频率比预期低了将近7%，设计缓冲结构可以有效缩减共振频率的减少量，其中双侧褶皱使共振频率减少量缩减至近1.3%．其原因是初始形态改变导致微桥两侧静电力不等，缓冲结构可以减少初始形态改变引起的静电变形．另外，在褶皱数量为2个以上时，缓冲结构对微桥共振频率的影响变化不大，双侧结构表现优于单侧结构．

在实际应用中，共振频率的变化会引起一系列的工程问题，设计适当的缓冲结构可以提高微机电产品的合格率．

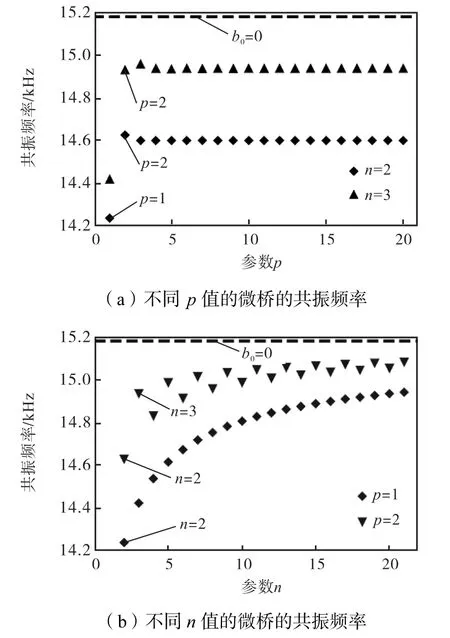
图6 不同初始形态的微桥共振频率Fig.6Resonant frequencies of micro-bridges with different initial shapes

3.3初始形态对幅频响应的影响

幅频响应是微梁的重要性质，例如在生物传感器、化学传感器中通过测量共振频率的漂移量来获取测量因子的变化．本节取控制参数：板间隙10µm，直流偏置电压VC=25 V，交流激励电压幅值VA=0.5 V ，拱高b0=2.5µm ，探讨初始形态控制参数p和n对幅频响应的影响．

图7所示是褶皱微桥和理想微桥的幅频曲线.可以看出，初始形态的改变对微桥的幅频响应关系影响显著：静电力引起的软化现象变得十分明显，同时共振频率减小，稳态幅值大幅增加．这会导致微器件的性能发生很大变化，例如，初始形态改变引起的弛豫现象使得高频开关滞后时间达到秒数量级而不能正常工作．增加褶皱数可以削弱初始形态改变引起的软化效应，但褶皱数为2个以上时，提升很小．

图8所示是存在初始挠形的微桥和理想微桥的幅频曲线．由图可知，微拱的曲率越小（n值减小），导致非线性项绝对值增大，从而静电力引起的软化现象越明显，共振频率越小，稳态幅值越大，增加褶皱会弱化这些现象；双侧褶皱结构削弱软化效应的能力强于单侧褶皱结构．

通过分析幅频响应与初始形态控制参数p和n的关系可知：微拱和理想微桥的动力学特性相差很多.单纯地增加褶皱或改变曲率只能减弱少部分初始挠形对微梁非线性行为和共振频率的影响，只有设计适当的缓冲结构才能保证微梁工作性能达到预期．

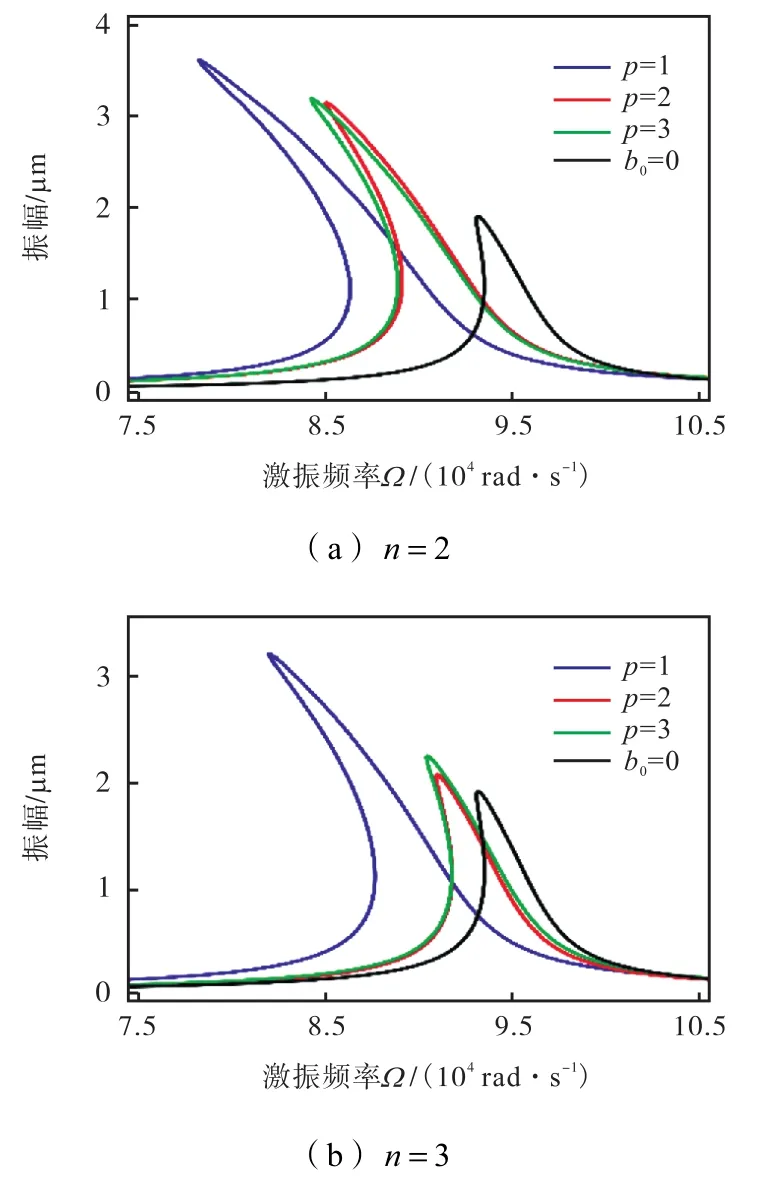
图7 不同p值的微桥的幅频曲线Fig.7 Amplitude-frequency response curves of microbridges affected by p

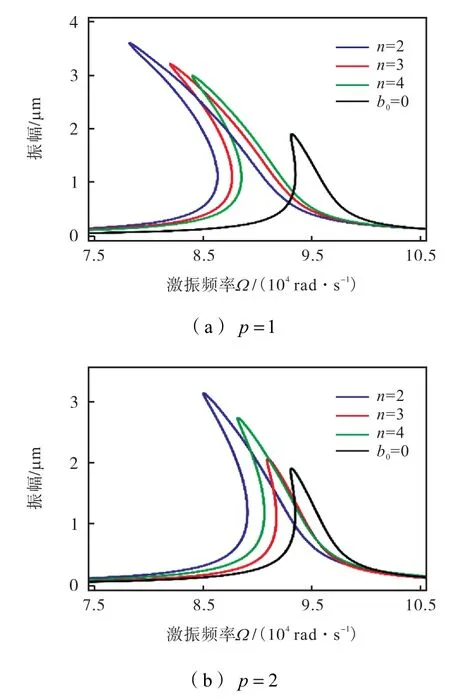
图8 不同n值的微梁的幅频曲线Fig.8 Amplitude-frequency response curves of microbeams affected by n

3.4典型微梁结构的动力学特性

褶皱微桥与理想微桥和微拱，三者之间动力学特性变化明显且具有代表性．取控制参数：板间隙10µm，直流偏置电压VC=25 V，交流激励电压幅值VA=0.5 V，拱高b0=2.5µm ，分析各微桥的动力学特性，见图9．受初始挠形影响，微桥共振频率减小，稳态幅值和共振漂移量增大；缓冲结构可以削弱初始挠形的影响，且双侧结构表现优于单侧结构．在工程中，需要利用微梁非线性行为的微器件（如微采集器）应选择设计单侧褶皱结构，既可以保证工作性能还可以降低能耗；需要避免微梁非线性行为的微器件（如微谐振器）应选择合适的双侧褶皱结构以保证工作性能．

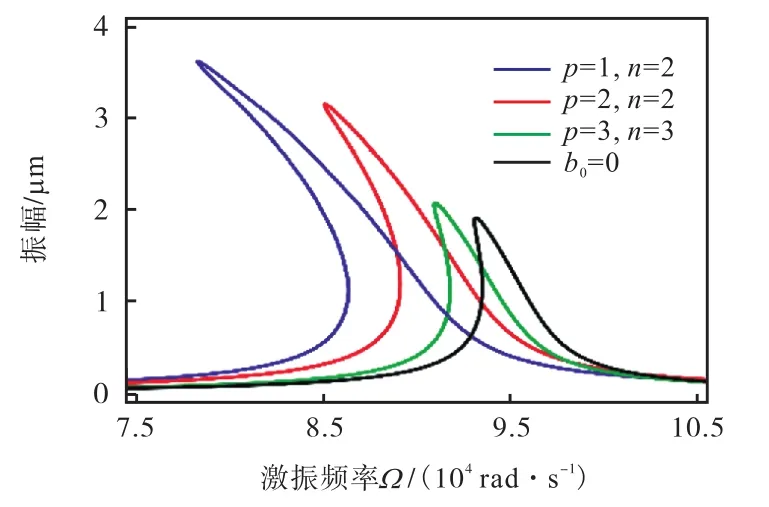
图9 不同形态微梁的幅频曲线Fig.9Amplitude-frequency response curves of microbeams with different shapes

3.5其他因素对微梁动力学特性的影响

静电驱动微梁结构动力学特性的主要控制参数为拱高、直流偏置电压、交流电压幅值和基板与极板间隙［7-14］．本节取微拱和双侧褶皱微桥为研究对象，探讨上述控制参数对微梁动力学特性的影响．

3.5.1拱高和板间隙影响

微梁的拱高由使用的牺牲层厚度和设计的缓冲结构决定．取控制参数：板间隙10µm，直流偏置电压VC=25 V ，交流激励电压幅值VA=0.5 V ，拱高b0为2.0µm、2.5µm和3.0µm．幅频响应曲线如图10所示，拱高增大，共振频率减小，稳态幅值增大，共振漂移量增加；拱高对双侧褶皱微桥的控制效果不明显．

板间隙的大小决定着微器件的最小可制造尺寸．取控制参数：直流偏置电压VC=25 V，交流激励电压幅值VA=0.5 V ，拱高b0=2.5µm ，板间隙为10.0 µm、12.5µm和15.0µm．幅频曲线如图11所示，随着板间隙减小，共振频率减小，稳态幅值增大，共振漂移量增加，双侧褶皱微桥的共振漂移量变化不明显．

通过分析拱高和板间隙对微桥动力学特性的影响可知，双侧褶皱结构可以大幅削弱拱高、板间隙对微梁非线性行为的影响；降低拱高和增大板间隙可以提高微梁的共振频率，减小稳态幅值．

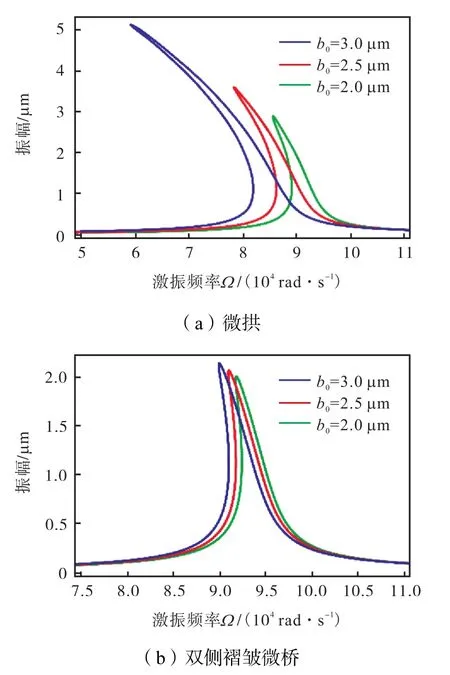
图10 不同拱高微桥的幅频曲线Fig.10 Amplitude-frequency response curves of microbridges with different arch heights

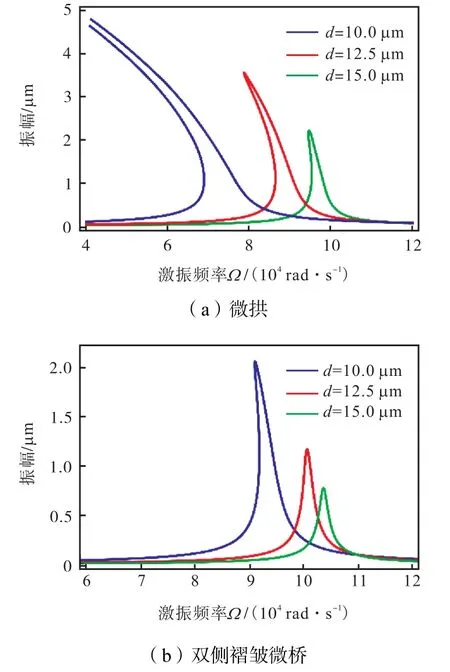
图11 不同板间隙下微桥的幅频曲线Fig.11 Amplitude-frequency response curves of microbridges under different spacings

3.5.2加载电压的影响

直流电压决定着静电驱动力的大小，交流电压决定着所需的能源输入．取控制参数：板间隙10µm，拱高b0=2.5µm ，探讨加载电压对微桥动力学特性的影响．图12是取交流激励电压幅值VA=0.5 V ，直流偏置电压VC为20 V、25 V和30 V时的幅频曲线．图13是取直流偏置电压VC=25 V，交流激励电压幅值VA为0.25 V、0.50 V和0.75 V时的幅频响应曲线.

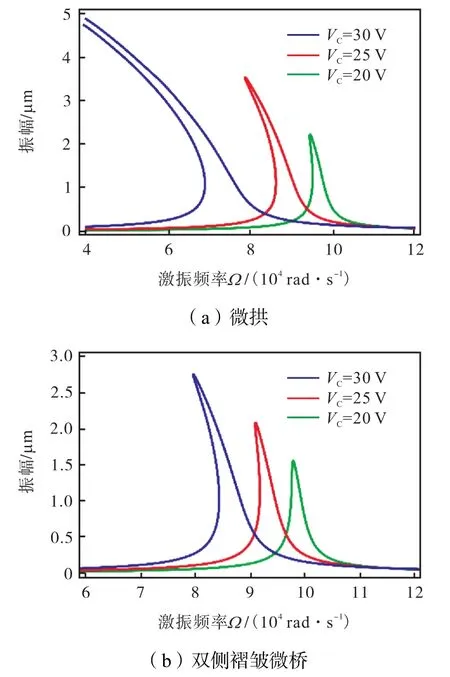
图12 不同直流偏置电压下微桥的幅频曲线Fig.12Amplitude-frequency response curves of microbridges under different DC bias voltages

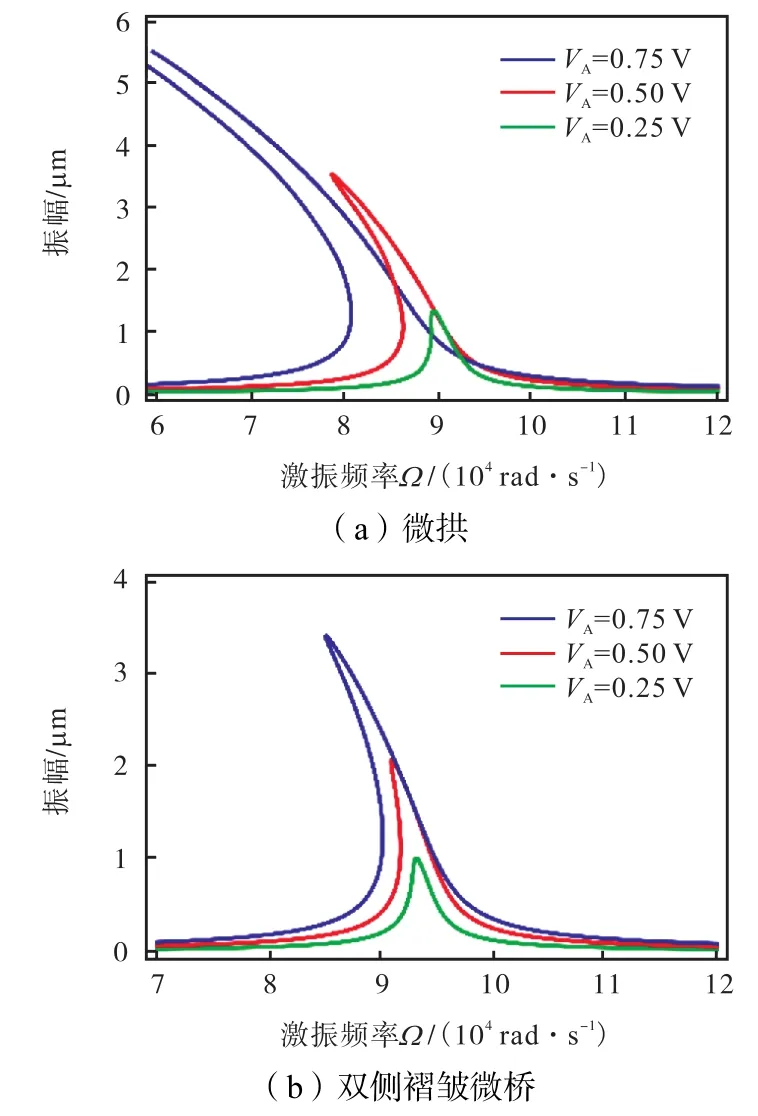
图13 不同幅值的交流电压下微桥的幅频曲线Fig.13Amplitude-frequency response curves of microbridges under different AC voltages

分析可知，随着直流偏置电压增大，共振频率减小，稳态幅值和共振漂移量增大；随着交流激励电压幅值增加，稳态幅值和共振漂移量增加，共振频率不发生变化；双侧褶皱结构可以大幅削弱静电力引起的软化效应．

4　结 论

（1） 初始形态改变会降低微系统的静电吸合电压，双侧翘曲结构可以大幅提高微器件的工作稳定性和精确度．

（2） 初始形态改变会降低微桥的共振频率，增大稳态幅值和共振频率漂移量，放大静电力引起的软化效应，在设计中不可忽略．

（3） 减小拱高或增大基板与极板间隙可提高微桥的共振频率，减小稳态幅值和共振频率漂移量．

（4） 增大直流偏置电压会减小共振频率，增大稳态幅值和共振漂移量，增大交流激励电压幅值会增大稳态幅值和共振漂移量，共振频率不变化．

（5） 设计缓冲结构可以削弱微桥的非线性行为，提高共振频率，降低稳态幅值和共振漂移量，双侧褶皱功能性强于单侧褶皱．

［1］ Rhoads J F，Shaw S W，Turner K L，et al. Generalized parametric resonance in electrostatically actuated microelectromechanical oscillators［J］. Journal of Sound and Vibration，2006，296（4/5）：797-829.

［2］ Hornstein S，Gottlieb O. Nonlinear dynamics，stability and control of the scan process in noncontacting atomic force microscopy［J］. Nonlinear Dynamics，2008，54（1/2）：93-122.

［3］ 朱长纯，赵红坡，韩建强，等. MEMS薄膜中的残余

应力问题［J］. 微纳电子技术，2003（10）：30-34.

Zhu Changchun，Zhao Hongpo，Han Jianqiang，et al. The residual stresses in MEMS thin films［J］. Micronanoelectronic Technology，2003（10）：30-34（in Chinese）.

［4］ 钱 劲，刘 澂，张大成，等. 微电子机械系统中的残余应力问题［J］. 机械强度，2001，23（4）：393-401. Qian Jin，Liu Cheng，Zhang Dacheng，et al. Residual stresses in micro-electro-mechanical systems ［J］. Journal of Mechanical Strength，2001，23（4）：393-401（in Chinese）.

［5］ 张向军. 微机电系统机械学［M］. 北京：清华大学出版社，2012. Zhang Xiangjun. Mechanics Fundamentals of MEMS［M］. Beijing：Tsinghua University Press，2012（in Chinese）.

［6］ 埃尔温斯波克，扬 森. 硅微机械加工技术［M］. 姜岩峰，译. 北京：化学工业出版社，2006. Elwenspoek M，Jansen H. Silicon Micromachining［M］. Jiang Yanfeng，Trans. Beijing：Chemical Industry Press，2006（in Chinese）.

［7］ Krylov S，Harari I，Cohen Y. Stabilization of electrostatically actuated microstructures using parametric excitation［J］. Journal of Micromechanics and Microengineering，2005，15（6）：1188-1204.

［8］ Krylov S，Ilic B R，Schreiber D，et al. The pull-in behavior of electrostatically actuated bistable microstructures［J］. Journal of Micromechanics and Microengineering，2008，18（5）：055026.

［9］ Krylov S，Dick N. Dynamic stability of electrostatically actuated initially curved shallow micro beams［J］. Continuum Mechanics and Thermodynamics，2010，22（6/7/8）：445-468.

［10］ Younis M I，Ouakad H M. The static and dynamic behavior of MEMS arches under electrostatic actuation［C］// Proceedings of the Sixth International Symposium on Mechatronics and Its Applications（ISMA09）. New York，USA，2009：ISMA09（1-6）.

［11］ Ruzziconi L，Younis M I，Lenci S，et al. Parameter identification of an electrically actuated imperfect microbeam［J］. International Journal of Non-Linear Mechanics，2013，57：208-219.

［12］ Ruzziconi L，Bataineh A M，Younis M I，et al. Nonlinear dynamics of an electrically actuated imperfect microbeam resonator：Experimental investigation and reduced-order modeling［J］. Journal of Micromechanics and Microengineering，2013，23（7）：075012.

［13］ Ruzziconi L，Lenci S，Younis M I. An imperfect microbeam under an axial load and electric excitation：Nonlinear phenomena and dynamical integrity［J］. International Journal of Bifurcation and Chaos，2013，23（2）：1350026.

［14］ Ouakad H M，Younis M I. The dynamic behavior of MEMS arch resonators actuated electrically［J］. International Journal of Non-Linear Mechanics，2010，45（7）：704-713.

［15］ Ouakad H M，Younis M I. On using the dynamic snapthrough motion of MEMS initially curved microbeams for filtering applications［J］. Journal of Sound and Vibration，2014，333（2）：555-568.

（责任编辑：金顺爱）

Dynamic Characteristics of Electrostatically Actuated Micro-Bridges Affected by Buffered Structure

Zhang Qichang，Chen Tao，Wang Wei
（Tianjin Key Laboratory of Nonlinear Dynamics and Chaos Control，School of Mechanical Engineering，Tianjin University，Tianjin 300072，China）

Dynamic behavior of movable components plays an important role in service behavior of micro-electromechanical systems（MEMS）．As a primary movable component，the dynamic characteristics of micro-bridges have attracted the attention of scholars who are in the research field of MEMS．Inevitably，initial shapes of the finished bridges which have been perfectly designed change because of the residual stress．Designing buffered structure is an important method to reduce the influence of residual stress．A dynamics model of micro-bridge system based on Euler-Bernoulli beam theory was presented．The multi-scale method was used to carry out the perturbation analysis on dynamic equations of micro-bridges．The effects of initial shape，the gap between based plate and electro-plate，the amplitudes of DC bias voltage and AC voltage on system’s resonance frequency and frequency-amplitude response were discussed in detail．Research shows that the initial deflection，and the amplitudes of DC bias voltage and AC voltage show softening effect and shift the resonant frequency to a smaller range．The softening effect enhances with the arch height increasing or the gap decreasing，and weakens with the curvature of micro-arches increasing．Buffered structure weakens the softening effect caused by initial deflection，and the weakening effect barely changes when the number of buffered folds is more than two，and the ability of bilateral warping in weakening the softening effect is better than that of single one.

micro-bridges；initial shapes；buffered structure；multi-scale method

O322

A

0493-2137（2016）07-0674-07

10.11784/tdxbz201507071

2015-07-23；

2015-09-16.

国家自然科学基金资助项目（11372210，11102127）；高等学校博士学科点专项科研基金资助项目（20120032110010）.

张琪昌（1959— ），男，博士，教授，qzhang@tju．edu．cn.

王 炜，wangweifrancis@tju．edu．cn.

网络出版时间：2015-09-25. 网络出版地址：http://www．cnki．net/kcms/detail/12.1127．N.20150925.1544.002．html.