基于EEMD时频谱二值化的振动信号微弱特征提取方法

王 鹏，王太勇，2，董靖川

（1. 天津大学机构理论与装备设计教育部重点实验室，天津 300072；2. 天津市数控系统技术工程中心，天津300072）

基于EEMD时频谱二值化的振动信号微弱特征提取方法

王 鹏1，王太勇1，2，董靖川1

（1. 天津大学机构理论与装备设计教育部重点实验室，天津 300072；2. 天津市数控系统技术工程中心，天津300072）

为实现时频域高维信息辅助的振动信号微弱瞬态特征增强，提出了一种多尺度时频谱二值化方法．通过高分辨率时频谱切片提取能量突变点，其权重为1，其余点权重为0．进行多次不同尺度的二进制谱分析并降维至时域，得到针对多目标频率的权重谱与权重向量，从而实现微弱冲击特征的增强．用仿真信号分析对该方法的可行性与准确性进行了验证，列车轴承故障诊断试验则进一步验证了该方法在信号微弱特征提取中的有效性．

集合经验模式分解；二进谱；特征提取；信号处理；故障诊断

时频谱分析是振动信号微弱特征提取的重要方法，能够体现信号瞬时能量分布［1］．常见的时频分析方法主要包括短时傅里叶变换［2-3］、Wigner高阶谱［4］、小波变换［5-6］、Hilbert-Huang变换［7-8］和局部均值分解［9］等．但在现实环境中，由于原始信号中包含大量噪声，其特征频率常被噪声淹没．为了能够从噪声背景中提取振动信号特征，在时频分析中常采用降噪方法，根据噪声自身特性将其识别并进行抑制．但采取降噪方法的同时，信号的有用部分也常会受到影响.为了在时频谱中最大限度地保留信号特征信息并在特征提取过程中尽可能降低噪声的影响，本文提出了一种集合经验模式分解（ensemble empirical mode decomposition，EEMD）时频谱二值化方法．通过多尺度二进谱分析得到信号的权重谱，将其向时域累计得到权重向量，从而实现微弱冲击特征的增强．

1　基本思想

基于EEMD的Hilbert-Huang变换不仅能够获得较其他方法更加优秀的时频分辨率，还能够降低模态混叠效应．本方法在其基础上对时频谱进行多尺度二值化处理，通过在多种观测尺度下寻找时频谱中由于冲击引发的能量突变点，得到多个反映冲击权重的二进谱．将多个不同尺度的二进谱进行叠加得到信号的权重谱，再将其降维至时域即计算权重向量，从而降低噪声干扰、增强微弱冲击特征，进而提高故障诊断的准确性．基于EEMD时频谱二值化的振动信号微弱特征提取方法算法流程如图1所示．

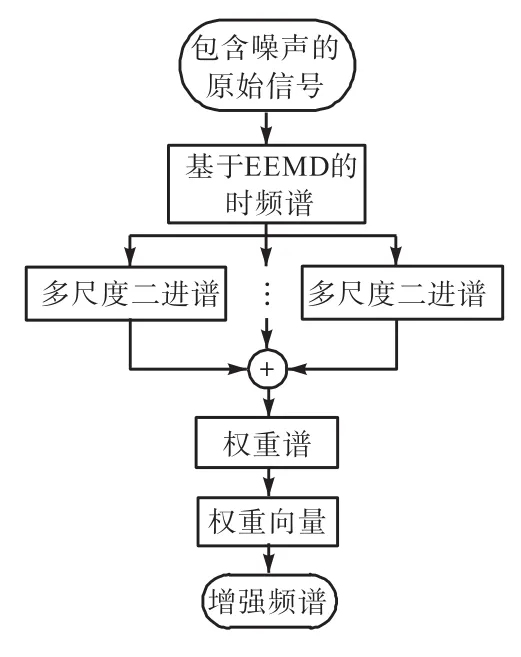
图1 算法流程Fig.1 Flow chart of algorithm

2　基于EEMD时频谱二值化的振动信号微弱特征提取方法分析流程

2.1基于EEMD的Hilbert-Huang变换

Hilbert-Huang变换是一种非参数化自适应时频分析方法，具有自适应、无交叉项干扰、时频分辨率高等特性［10］．作为Hilbert-Huang变换的核心部分，经验模式分解（empirical mode decomposition，EMD）起到了信号筛分解调的作用，其算法流程如图2所示．经过EMD筛分，可以得到多个频率-幅值简单调制且瞬时频率有意义的本征模态函数（intrinsic mode function，IMF）．

然而EMD方法也存在一定缺陷，如存在端点效应、模态混叠和虚假分量等［11］．为了抑制模态混叠和减少虚假分量，Wu等［12］提出了噪声辅助的集合经验模态分解，通过在原信号中添加时域均值为0的白噪声来均布原信号的极值点，使信号均匀、连续．为了减少添加白噪声造成的信号信噪比降低等因素对分析结果的影响，采取多次添加噪声、多次EMD分析、多IMF集合平均的方法．经过m次添加不同噪声的EMD，最终得到的n个IMF为

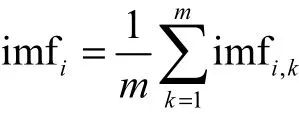
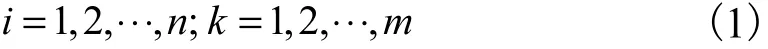
原信号也可由得到的n个IMF及残余分量rn（t）表示为

通过Hilbert 变换求取各IMF的瞬时频率ω（t）和瞬时幅值α（t），则原信号可表示为

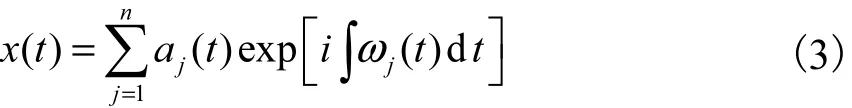
从而得到原信号的时频谱．

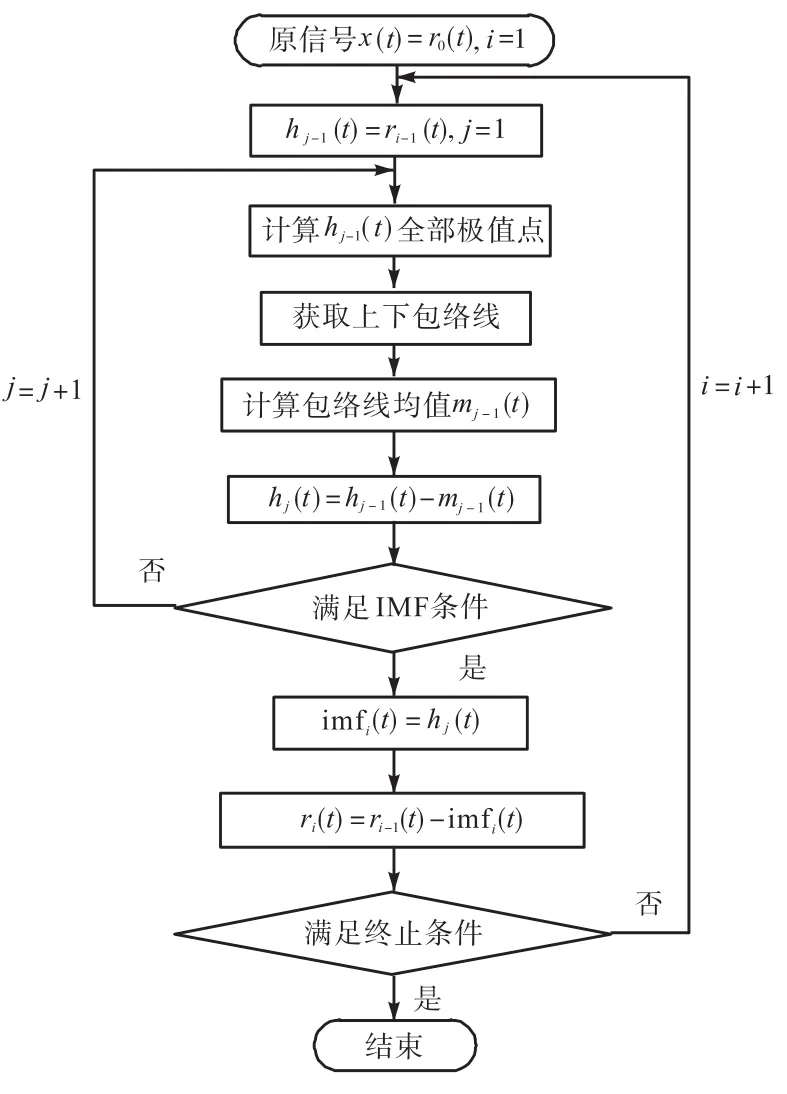
图2 EMD算法流程Fig.2 Flow chart of the EMD algorithm

2.2多尺度二进谱分析

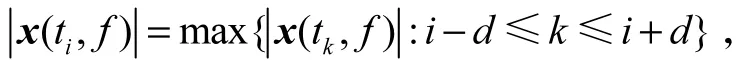
二进谱能够反映信号中冲击成分的存在性，其中值为1的点位表明存在能量突变，即为冲击赋予值为1的权重．与之相对，无冲击处的权重为0．在计算二进谱的过程中，间隔常数d的选择决定了二进谱的分析尺度．为了能够对振动信号特征进行更加有效的增强，需要通过选取不同的参数d进行多次不同尺度的二进谱分析，其选取方法为

式中：fs为信号采样频率；ff为所关注的特征频率；「x」为取不大于x最大整偶数．通过多次计算，可以得到多个二进谱B1（ti，f），B2（ti，f），…，Bc（ti，f）．

2.3时频谱增强

最后，对权重向量进行功率谱分析，即可提取出振动信号的微弱特征．

3　仿真信号分析

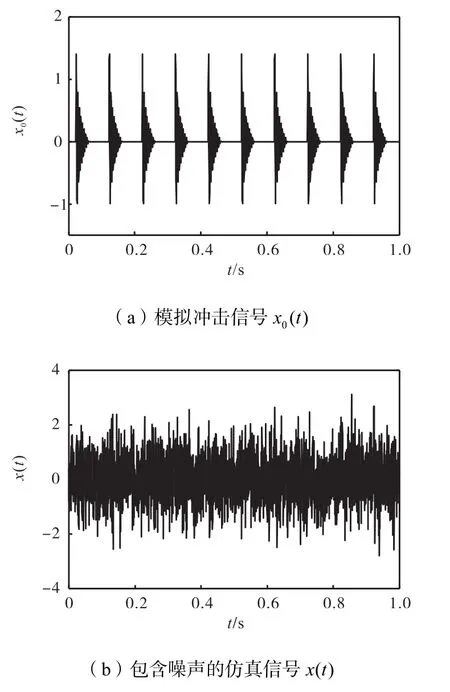
图3 仿真信号Fig.3 Simulated signals

如图3（a）所示，信号x0（t）模拟了轴承故障产生的周期性高频冲击，其信号长度为1，s，包含了10个由阻尼正弦信号模拟的冲击．将高斯白噪声信号添加到模拟冲击信号x0（t）中，得到如图3（b）所示的仿真信号x（t），信号采样频率为2，560，Hz．通过图3可以看出，冲击信号已经完全被噪声淹没．由于噪声信号呈现全频带分布的特性且能量较大，因此采用降噪、解调方法提取冲击信号特征较为困难．图4为仿真信号包络谱，可以看出冲击特征频率及其倍频被噪声淹没．

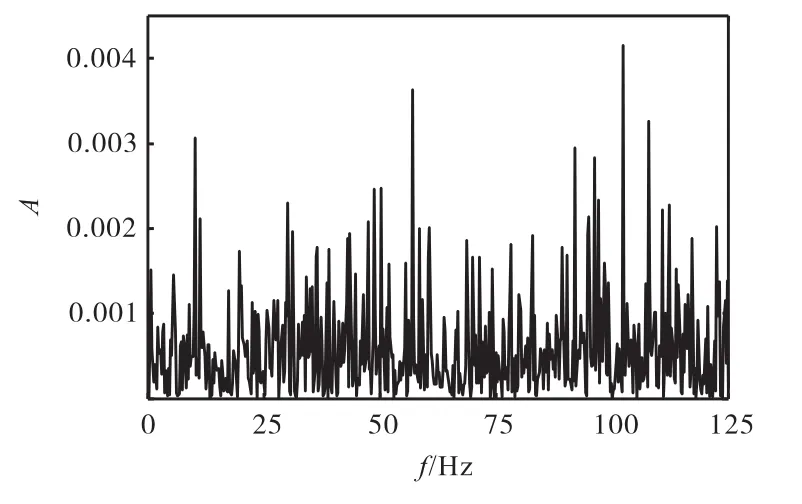
图4 仿真信号包络谱Fig.4 Envelope spectrum of simulated signals

采用EEMD方法直接对信号进行解调，获取11个IMF分量，由此获得的时频谱如图5所示．可以看出，信号中存在较多的噪声成分，时频谱图像较为杂乱，无法直接观察到40，Hz的冲击信号成分．

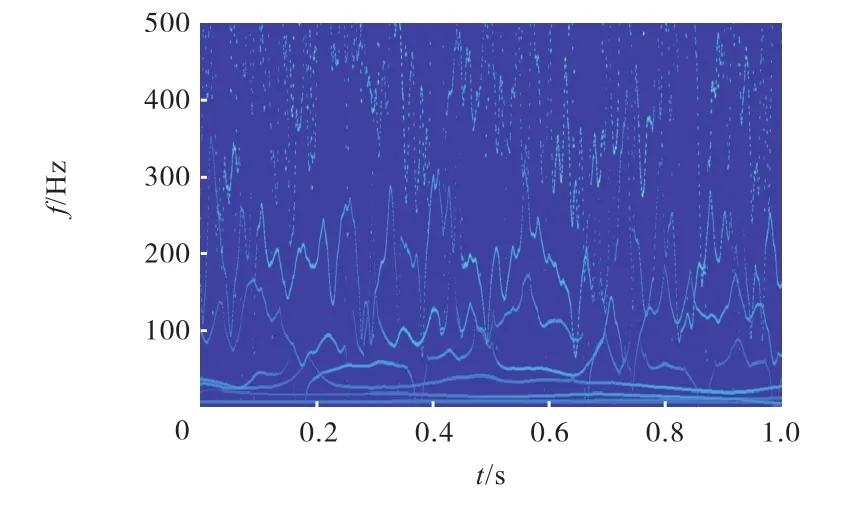
图5 仿真信号的时频谱Fig.5 Time-frequency map of simulated signal

对图5的时频谱进行多尺度二值化，式（4）中的参数设定为fs=2560 Hz ，ff=10 Hz ．在第1次运算中，选择二进谱计算特征尺度d1=128，计算得到的二进谱如图6（a）所示．重复该过程，分别进行特征尺度d2=256，d3=384，d4=512的二进谱计算，其结果依次如图6（b）、6（c）和6（d）所示．

将得到的4个不同尺度的二进谱相加，得到图7所示的权重谱．对其进行降维，将权重值累计至时域，得到如图8所示的权重向量．对权重向量进行功率谱分析，得到如图9所示的频谱，从图中可以清晰地看到10，Hz处的冲击特征频率以及其倍频．

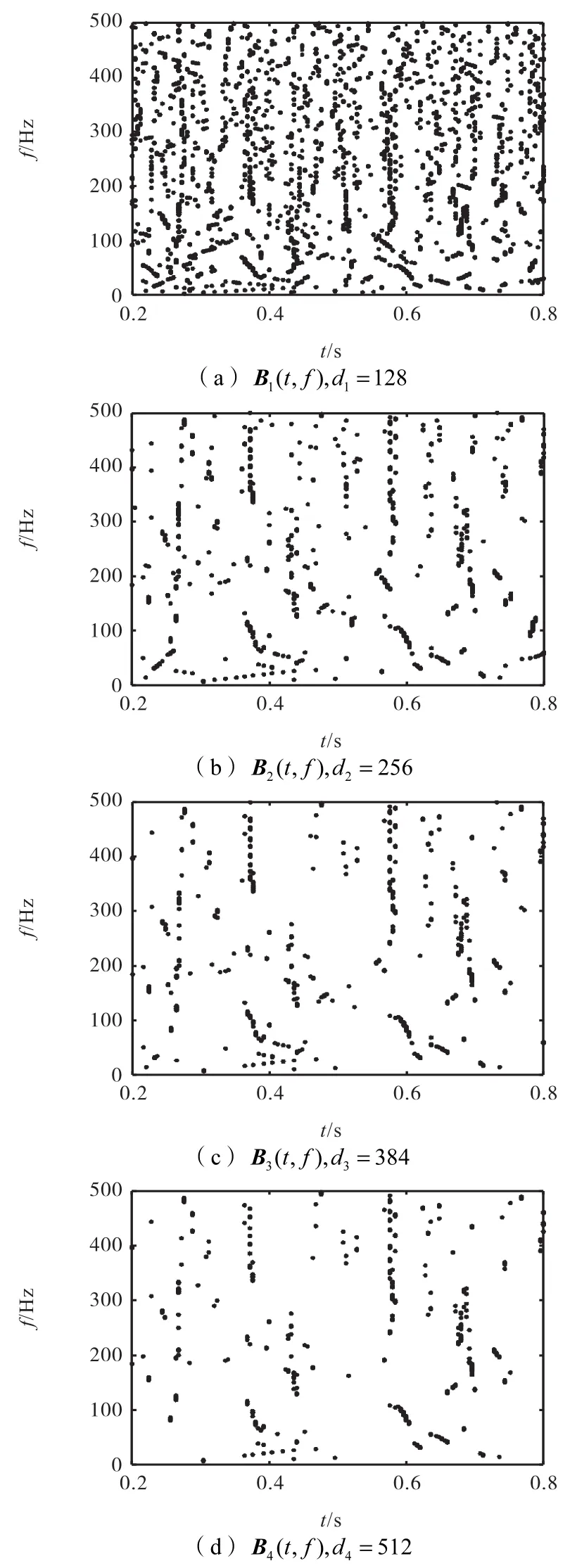
图6 仿真信号的多尺度二进谱Fig.6 Multi-scale binary spectra of simulated signals

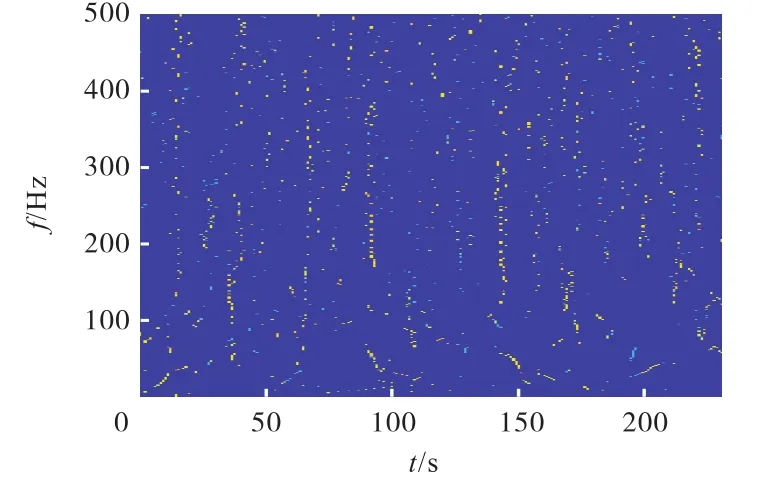
图7 仿真信号的权重谱Fig.7 Weight spectrum of simulated signal

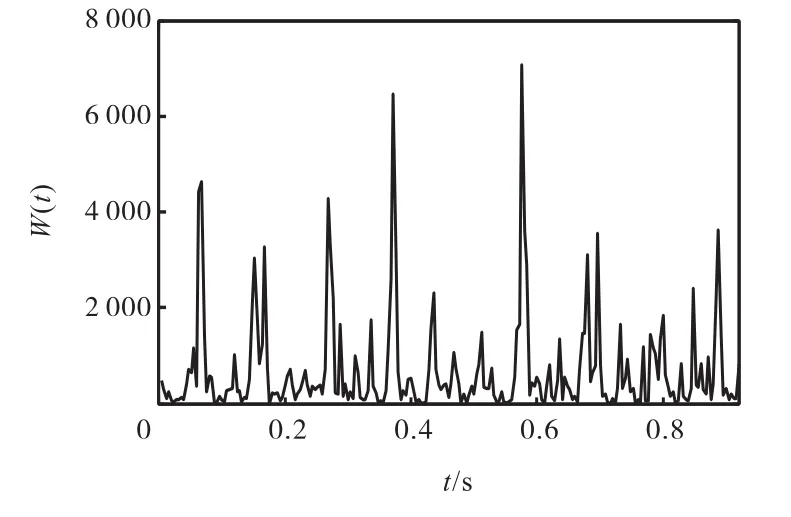
图8 仿真信号的权重向量Fig.8 Vector of weights of simulated signal

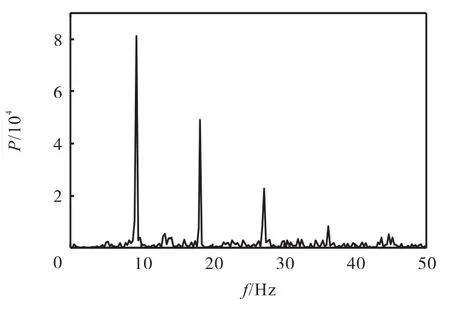
图9 权重向量的功率谱（仿真信号）Fig.9 Power spectrum of vector of weights（simulated signal）

4　轴承诊断试验

为验证该方法在实际测试中的有效性，进行了列车轴承故障诊断试验．试验采用的轮对试验台包含了装配有轴承的轮对、电机驱动系统、托举装置以及整体框架．托举装置通过顶升两侧轴承进行轮对定位，电机带动橡胶轮摩擦车轮内侧面起到传动作用．在车轮两端分别装配有型号为352226x2-2z的正常轴承和外圈故障轴承，轴承参数与故障特征频率如表1所示．对外圈故障轴承振动加速度信号X（t）进行采集、分析，传感器采用图10的方式进行磁座固定．

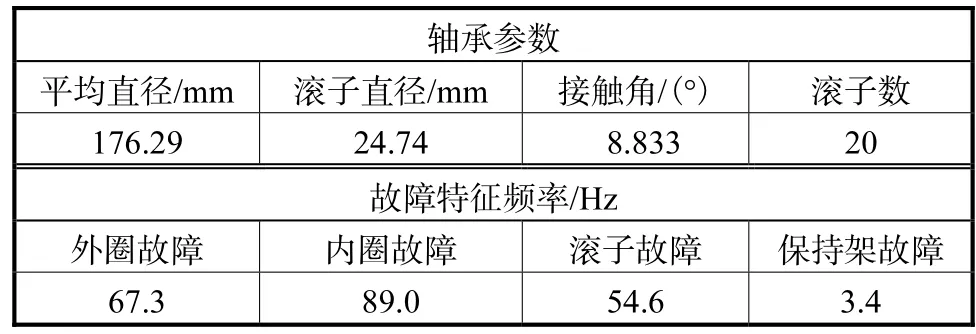
表1 352226x2-2z轴承参数与故障特征频率Tab.1Parameters and fault frequencies of 352226x2-2z bearing

选取垂直方向布置的传感器采集到的信号进行分析，信号采样频率为5，120，Hz，采样时长为2，s，采集到的信号如图11所示．对其进行包络谱分析，得到如图12所示的结果，从中无法看出故障特征频率成分．

图10 传感器布置Fig.10 Arrangement of transducers

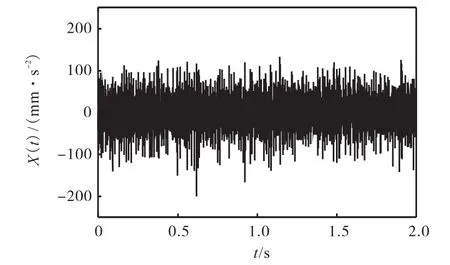
图11 外圈故障轴承振动信号Fig.11 Vibration signal of outer-race fault bearing vibration signal

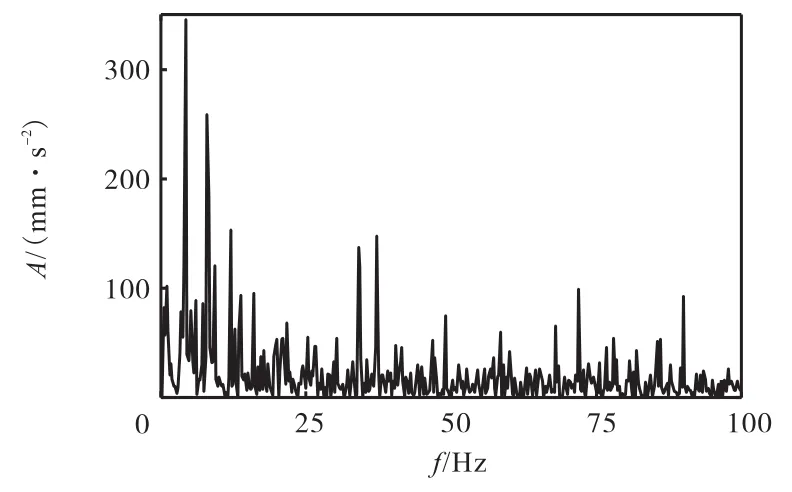
图12 外圈故障轴承振动信号的包络谱Fig.12 Envelope spectrum of outer-race fault bearing vibration signal

采用EEMD方法直接对信号进行解调，获取10个IMF分量，由此获得的时频谱如图13所示．

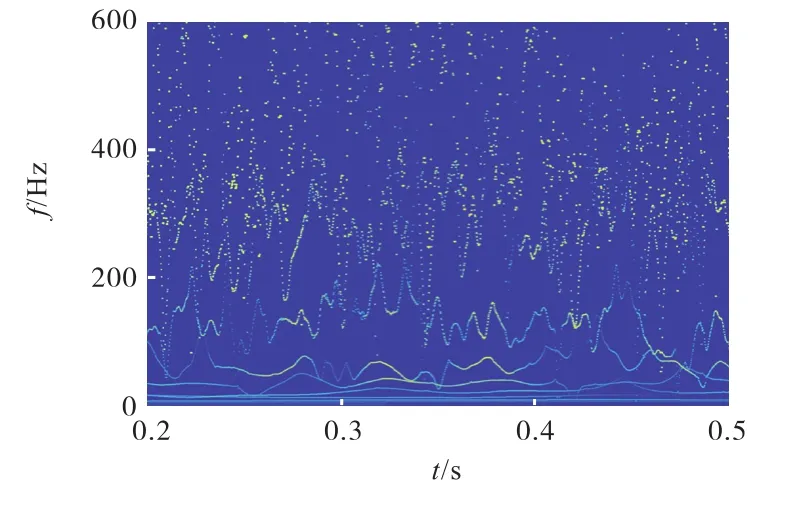
图13 外圈故障轴承振动信号的时频谱Fig.13 Time-frequency map of vibration signal of outerrace fault bearing

对图13的时频谱进行多尺度二值化，式（4）中的参数设定为fs=5 120 Hz ．在轴承故障未知的情况下，需考虑轴承所有故障可能，因此需进行针对所有故障特征频率的时频谱多尺度二值化．依据故障特征频率从低到高的原则，首先选取针对保持架故障ff=3.4 Hz 的d1=752，d2=1 504，分别得到如图14所示的二进谱．

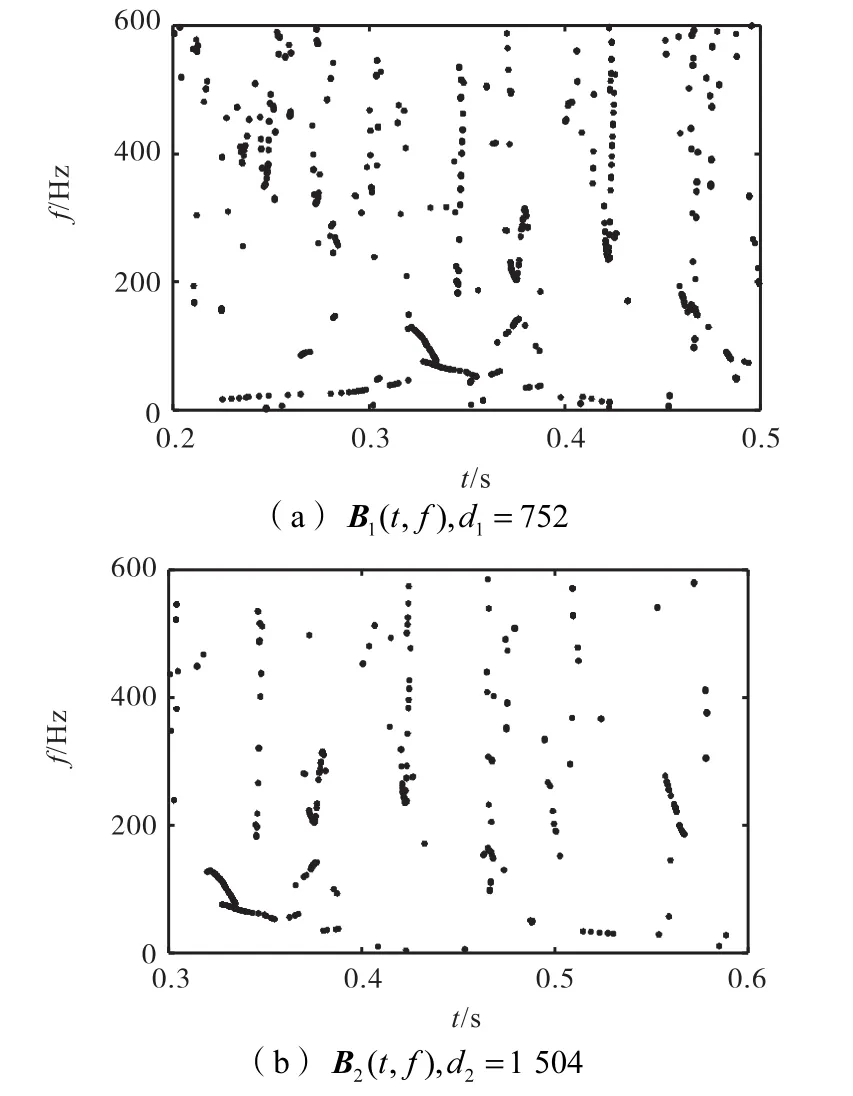
图14 针对保持架故障的多尺度二进谱Fig.14 Multi-scale binary spectra for cage fault detection

选取针对滚子故障ff=54.6 Hz 的d3=46和d4=92，得到如图15所示的二进谱．

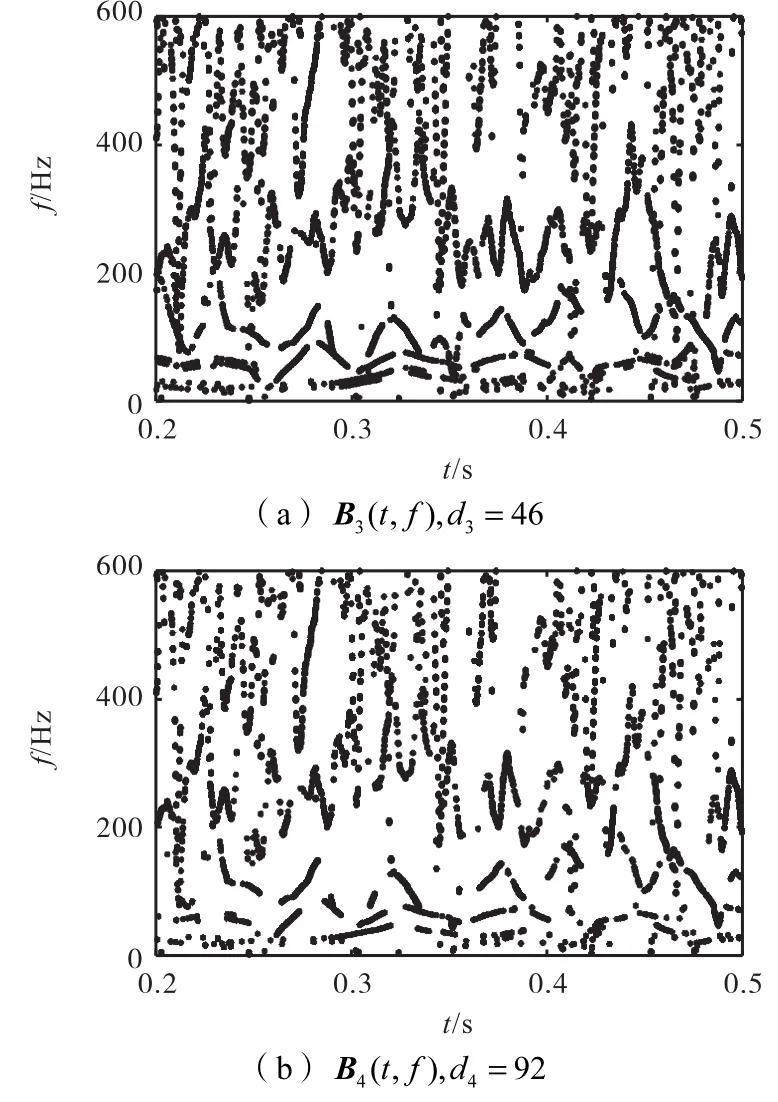
图15 针对滚子故障的多尺度二进谱Fig.15 Multi-scale binary spectrum for roller fault detection

选取针对外圈故障ff=67.3Hz 的d5=38和d6=76，得到如图16所示的二进谱．

选取针对滚子故障ff=89.0 Hz 的d7=28和d8=56，得到如图17所示的二进谱．

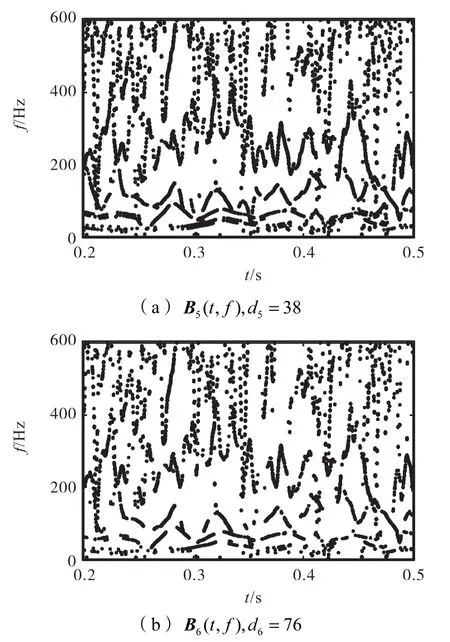
图16 针对外圈故障的多尺度二进谱Fig.16 Multi-scale binary spectra for outer-race fault detection

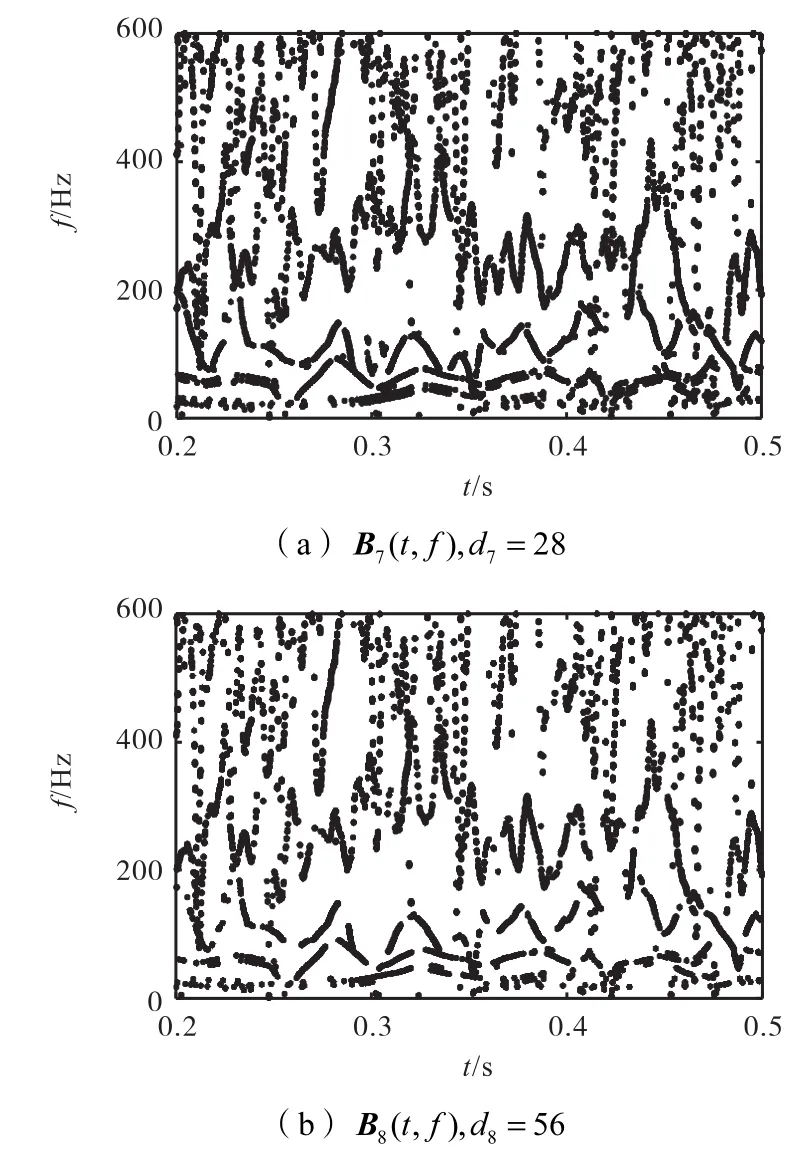
图17 针对内圈故障的多尺度二进谱Fig.17 Multi-scale binary spectra for inner-race fault detection

将得到的8个不同尺度的二进谱相加，得到如图18所示的权重谱．对其进行降维，将权重值累计至时域，得到如图19所示的权重向量．对权重向量进行分析，得到如图20所示的功率谱．

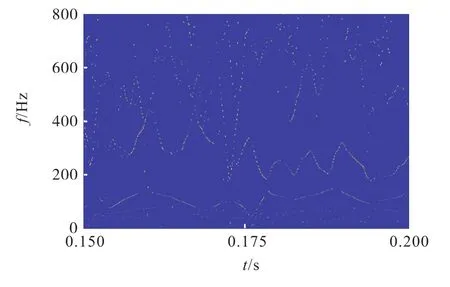
图18 外圈故障轴承振动信号的权重谱Fig.18Weight spectrum of vibration signal of outer-race fault bearing

图19 外圈故障轴承振动信号的权重向量Fig.19Vector of weights of vibration signal of outer-race fault bearing

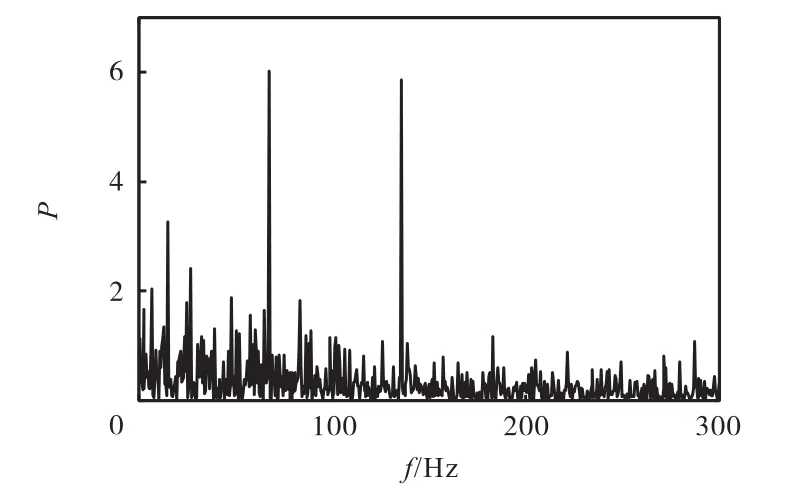
图20 权重向量的功率谱（外圈故障轴承振动信号）Fig.20Power spectrum of vector of weights（vibration signal of outer-race fault bearing）

通过试验可以看出，虽然原始振动信号中包含了大量噪声，采用常用的包络谱分析方法无法得到能够反映故障的特征成分，但经过针对各种故障特征频率的二进谱分析与权重分析，可以成功提取轴承外圈故障特征．67.3，Hz处的外圈故障特征频率及134，Hz处的倍频清晰，且图中不存在明显的与其他故障相关的特征频率，因此可以判定该轴承仅存在外圈故障．

5　结 语

基于EEMD时频谱二值化的振动信号微弱特征提取方法，在高分辨率时频谱分析的基础上，提出了一种多尺度时频谱二值化方法．以此为核心完成了从时频谱到二进谱再到权重向量的多次降维过程，最终实现了多分析尺度下振动信号微弱特征的增强与提取．

通过仿真信号分析与列车轴箱轴承故障诊断试验对该方法进行了验证；通过与包络谱分析方法的对比，证明了该方法的有效性．结果表明该方法能够有效地从强噪声污染的信号中提取故障相关特征，对实际故障进行有效筛查．

［1］ Feng Z，Liang M，Chu F. Recent advances in timefrequency analysis methods for machinery fault diagnosis：A review with application examples［J］. Mechanical Systems and Signal Processing，2013，38（1）：165-205.

［2］ 王天杨，李建勇，程卫东. 基于瞬时故障特征频率趋势线和故障特征阶比模板的变转速滚动轴承故障诊断［J］. 振动工程学报，2015，28（6）：1006-1014. Wang Tianyang，Li Jianyong，Cheng Weidong. The instantaneous fault characteristic frequency and fault characteristic order template based fault diagnosis algorithm for rolling bearing under time-varying rotational speed［J］. Journal of Vibration Engineering，2015，28（6）：1006-1014（in Chinese）.

［3］ 郭远晶，魏燕定，周晓军. 基于STFT时频谱系数收缩的信号降噪方法［J］. 振动、测试与诊断，2015，35（6）：1090-1096，1201. Guo Yuanjing，Wei Yanding，Zhou Xiaojun. Signal denoising method based on STFT time-frequency spectrum coefficients shrinkage［J］. Journal of Vibration，Measurement & Diagnosis，2015，35（6）：1090-1096，1201（in Chinese）.

［5］ Bianchi D，Mayrhofer E，Gröschl M，et al. Wavelet packet transform for detection of single events in acoustic emission signals［J］. Mechanical Systems and Signal Processing，2015，64/65： 441-451.

［6］ Chandra N H，Sekhar A S. Fault detection in rotor bearing systems using time frequency techniques［J］. Mechanical Systems and Signal Processing，2016，72/73： 105-133.

［7］ Lee J，Wu F，Zhao W，et al. Prognostics and health management design for rotary machinery systems： Reviews，methodology and applications［J］. Mechanical Systems and Signal Processing，2014，42（1/2）：314-334.

［8］ Song Mei，Chen Tao. Instantaneous 3D EEG signal analysis based on empirical mode decomposition and the Hilbert-Huang transform applied to depth of anaesthesia［J］. Entropy，2015，17（3）：928-949.

［9］ Wang Y，He Z，Zi Y. A comparative study on the local mean decomposition and empirical mode decomposition and their applications to rotating machinery health diagnosis［J］. Journal of Vibration and Acoustics，2010，132（2）：613-624.

［10］ Huang N E，Shen Z，Long S R，et al. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis［J］. Proceedings of the Royal Society A：Mathematical Physical & Engineering Sciences，1998，454：903-995.

［11］ Huang N E，Wu Z，Long S R，et al. On instantaneous frequency［J］. Advances in Adaptive Data Analysis，2009，1（2）：177-229.

［12］ Wu Z，Huang N E. Ensemble empirical mode decomposition：A noise-assisted data analysis method［J］. Advances in Adaptive Data Analysis，2009，1（1）：1-41.

（责任编辑：金顺爱）

Weak Feature Extraction of Vibration Signal Based on Binaryzation of EEMD Time-Frequency Map

Wang Peng1，Wang Taiyong1，2，Dong Jingchuan1
（1. Key Laboratory of Mechanism Theory and Equipment Design of Ministry of Education，Tianjin University，Tianjin 300072，China；2. Tianjin Engineering Research Center of Numerical Control Technology，Tianjin 300072，China）

A multi-scale binaryzation method of time-frequency map was proposed to enhance the weak instant features of vibration signal with high dimensional information assist in time-frequency domain．The method extracts energy fluctuations in slices of high definition time-frequency map by weighting the points of energy fluctuation as 1 and other points as 0．Repeat the process of binary spectrum analysis with different scales and utilize dimensionality reduction to time domain．Then the weight spectrum and vector of weights are obtained to enhance the weak shock features．Simulated signal processing confirms the validity and accuracy of this method．Train bearing experiment verifies the effectiveness of the method in weak feature extraction of vibration signal.

ensemble empirical mode decomposition（EEMD）；binary spectrum；feature extraction；signal processing；fault diagnosis

TH17；TH165.3

A

0493-2137（2016）07-0667-07

10.11784/tdxbz201603051

2016-03-18；

2016-04-22.

国家自然科学基金委员会与中国民航局联合资助项目（U1533103）；国家自然科学基金资助项目（51475324）.

王 鹏（1987— ），男，博士研究生，pengwang@tju.edu.cn.

王太勇，tywang@189.cn.