B08RDP区域集合预报温度场质量评估与综合偏差订正
马旭林,周勃旸,时洋②,计燕霞,和杰

B08RDP区域集合预报温度场质量评估与综合偏差订正
马旭林①*,周勃旸①,时洋①②,计燕霞①,和杰①
① 南京信息工程大学 气象灾害教育部重点实验室,江苏 南京 210044;
② 广东省气象台,广东 广州 510080
2014-11-24收稿,2015-06-21接受
国家自然科学基金资助项目(41275111;91437113);公益性行业(气象)科研专项(GYHY201506005)
针对B08RDP(The Beijing 2008 Olympics Research and Development Project)5套区域集合预报资料,系统分析了各套集合预报温度场的预报质量。在此基础上运用集合预报的综合偏差订正方法对温度场进行偏差订正,并对其效果进行了分析讨论。结果显示:5套B08RDP区域集合预报中,美国国家环境预报中心(NCEP)区域集合预报温度场的整体预报质量最高,平均预报误差最小,离散度也最为合理,预报可信度和可辨识度均较优;而中国气象科学研究院(CAMS)的温度预报误差过大,预报质量最差。整体上看,除NCEP之外的4套集合预报的温度场均存在集合离散度偏小的问题;综合偏差订正能有效减小各集合预报温度场的集合平均均方根误差,改善集合离散度的质量,显示出综合偏差订正方案对集合预报温度场偏差订正的良好能力。
数值预报
集合预报
偏差订正
质量评估
B08RDP
数值预报模式及其初始场的不确定性,导致非线性运动大气的确定性预报技巧受到限制。集合预报能够较好地反映实际大气运动不确定性特征,有效弥补了确定性预报的不足,已成为提高预报准确性的有效方式,既是概率预报的基础(智协飞等,2014a),也是目前集合——变分混合资料同化的前提(马旭林等,2014)。集合预报的关键问题之一是集合初始扰动的构造,主要包括基于初值或模式不确定性的构造方案。前者主要有欧洲中期天气预报中心(ECMWF)的集合同化——奇异向量法、美国环境预报中心(NCEP)的重新尺度化集合变换法(ETR,Ensemble Transform with Rescaling)和加拿大气象中心的集合卡尔曼滤波法(EnKF),以及基于集合卡尔曼理论发展的集合卡尔曼变换(ETKF)初始扰动方法(Wang and Bishop,2003;马旭林等,2008;Ma et al.,2009)等;后者通常可分为单模式多物理过程、多模式单物理过程以及多模式多物理过程(超级集合预报)等,其中超级集合预报方法的预报效果多优于单模式和多模式的集合平均(Krishnamurti et al.,2007;智协飞等,2013;崔慧慧和智协飞,2013)。
由于全球集合预报分辨率较低,难以有效捕获中小尺度天气系统的信息,从而具有较高分辨率的区域集合预报得到了快速发展(Bowler et al.,2009),并在数值天气预报业务中得到广泛应用。如NCEP早期采用增长模繁殖法构造初始扰动的短时区域集合预报系统(Du et al.,2003),目前由基于ETR方法的NCEP全球集合预报提供边界条件(麻巨慧等,2011),并考虑了模式不确定性(Du et al.,2006)。由ECMWF全球集合预报降尺度构造的COSMO-LEPS区域集合预报系统也具有较好的预报性能(Marsigli et al.,2008)。加拿大采用集合卡尔曼滤波(EnKF)方法发展了区域集合预报系统,并对不同的对流凝结参数和次网格尺度物理倾向进行随机扰动(Li et al.,2008;Charron et al.,2010)。英国气象局则由ETKF初始扰动的全球集合预报降尺度形成了区域集合预报系统MOGREPS(The Met Office Global and Regional Ensemble Prediction System),同时使用随机对流涡度考虑次网格不确定性(Bowler et al.,2009)。基于尺度混合方法(Wang et al.,2010,2014)构造的奥地利区域集合预报系统(Wang et al.,2011),将全球集合预报大尺度扰动信息与区域集合预报的中小尺度信息相结合,较好地反映了实际大气多尺度的不确定性特征,也有效改善了预报性能。日本气象厅则在非静力模式的基础上利用奇异向量法作为初始扰动方案建立了区域集合预报系统(Saito et al.,2006),也表现出良好的效果。
2008年为北京奥运会提供支撑的B08RDP(The Beijing 2008 Olympics Research and Development Project)项目(Duan et al.,2012)集中了6个预报中心的区域集合预报系统制作同一时间、相同区域的中尺度集合预报,其中客观评估各中心区域集合预报的整体预报质量和比较其预报性能是B08RDP项目的主要目标之一(Duan et al.,2012)。集合预报质量评估已开展了诸多研究(智协飞等,2014b),但评估物理量多选取海平面气压、500 hPa高度场或2 m温度等(Johnson and Swinbank,2009;Alexander et al.,2009),较少关注对流层低层的集合预报质量。对于区域集合预报,对流层低层的温度、位势高度以及湿度等对中小尺度天气系统的发生发展通常起着关键作用,也是反映区域集合预报性能的重要方面。因此,本文利用B08RDP项目的区域集合预报资料,首先对反映集合预报整体质量的对流层低层(850 hPa)温度预报质量进行多角度评估分析。然后,运用基于自适应卡尔曼滤波的递减平均方法(Du et al.,2007;Cui et al.,2012;马旭林等,2015),分别对各套集合预报的温度变量进行综合偏差订正,合理调整集合平均预报误差和集合离散度,进一步改善区域集合预报的整体质量,为实际预报业务中更好的应用区域集合预报产品提供参考。
1 B08RDP区域集合预报资料
B08RDP项目是中国气象局为2008年北京奥运会的成功举办提供天气预报支持,充分发挥多个集合预报中心的区域集合预报的优势,提高天气预报准确性而建立的联合项目。该项目共有国家气象中心(NMC)、中国气象科学院(CAMS)、美国国家环境预报中心(NCEP)、日本气象厅(JMA)气象研究所、奥地利气象局(ZAMG)、加拿大环境部数值预报研究中心等6家单位组成。其中,CAMS使用我国自行研发的非静力中尺度全球/区域同化预报系统GRAPES(陈德辉等,2008;马旭林等,2009)作为集合预报的预报模式,而NMC使用WRF作为区域集合预报模式,二者的初始扰动构造方案同为增长模繁殖法,边界条件均由NCEP全球ETR初始扰动集合预报提供,同时采用多积云对流参数、边界层及陆面过程方案构造模式扰动。其他中心的区域集合预报系统的配置参考文献Duan et al.(2012)。
因加拿大环境部数值预报中心的资料不完整,研究中只选取B08RDP项目中其余5套区域集合预报850 hPa温度场资料进行预报质量的评估分析和综合偏差订正,并考察偏差订正后各集合预报质量的改善程度。NMC的集合扰动成员数为15个,CAMS为9个,NCEP、JMA和ZAMG分别为15、11和17个集合扰动成员。共同的预报区域为(90~140°E,25~50°N),模式分辨率为15 km,预报时效为36 h,时间间隔为6 h。资料的时间长度为2008年6月24日—8月24日,共62 d。检验分析资料为ECMWF高分辨率再分析资料,其分辨率与资料区域均与集合预报资料一致。
2 质量评估
集合预报的质量主要可以从预报可靠性及预报可辨识度两个方面衡量。预报可靠性用来评价集合预报对不同预报概率对应的观测频率无偏估计的能力,主要反映集合预报与相应观测在统计学上的一致性(Wilks,2006),可用集合平均均方根误差(RMSE)、可信度曲线以及Talagrand分布等评价;而集合预报可辨识度是指集合预报区分未来不同天气事件的能力,一般采用可信度曲线、ROC(Relative Operating Characteristic)曲线等进行评价。

图1 850 hPa温度集合预报的RMSE(a)和r比值(b)Fig.1 The (a)RMSE and (b)r scores of temperature at 850 hPa for the five sets of ensemble forecasts
2.1集合预报可信度
RMSE可以用来对比各集合预报的预报准确性,即衡量集合平均的预报可靠性。图1a为5套集合预报资料的850 hPa温度场集合平均均方误差在36 h预报时效内的分布。可以看出,CAMS与NMC两套资料的RMSE较大,而JMA、NCEP、ZAMG三套资料则相对较小,其中CAMS的6 h集合平均预报偏差约为ZAMG的5倍,说明不同中心的集合平均预报的可靠性具有明显的差异。另外,CAMS的RMSE几乎是NMC近两倍,而CAMS与NMC两套集合预报除预报模式不同、集合成员数略有差异之外,其余集合预报系统特征均一致,可以说明集合预报中预报模式和集合成员数对集合预报平均的可靠性具有重要影响。
本次研究得出,在条件允许的情况下尽量应用多种方法联用进行诊断,以减少伪影干扰及患者个人病症发展状况对诊断的影响,而MRI结合MRA的筛查方案价格可能对于部分患者来说,存在一定的经济负担,此外,患者图像的判断也需要医师的经验,所以应尽可能选择经验较为丰富的医师进行图像分析,以保证诊断的准确性。
集合离散度主要反映集合成员描述实际大气运动状态不确定性的能力,理论上其量值应与集合平均预报误差相当。r是集合平均的预报误差(RMSE)与集合离散度(spread)的比值,可用来衡量集合离散度相对于集合平均预报误差的合理程度,理想情况下r为1。比较5套集合预报资料的850 hPa温度场r评分(图1b)可知,NCEP的集合离散度最为合理,6~36 h预报的r均位于1附近,而其余集合预报均明显大于1,尤其CAMS更为显著。这说明,除NCEP的集合预报外,其余集合预报的集合离散度均显著偏小。另外,CAMS、NMC和JMA集合预报的r值随着预报时间的增加有明显减小的趋势,而RMSE(图1a)并未有相应的显著增长或下降,说明这三套集合预报的集合离散度随预报时间的增加有增大趋势,显示出集合预报的不确定性越来越大,但仍未能反映实际大气运动的不确定性特征大小的程度。另外也反映出,这三个中心的集合预报平均预报偏差过大,可能主要与预报模式性能或模式初值的质量相关。
Talagrand图主要用来评价集合离散度代表观测不确定性的程度,即评估集合成员与观测之间的一致性(Wilks,2006)。Talagrand通过统计观测落在由大到小排列的集合成员区间内的频率而获得,理想的集合预报各集合成员与观测满足一致性条件,所有次序统计值相同(图中横直线),呈水平均一形态。图2为5套集合预报资料的Talagrand分布,图中横坐标的区间数与各自不同的集合成员数相对应。由图可知,NCEP集合预报各成员之间基本呈水平分布,相对为最优;ZAMG与JMA各集合成员间过于相似且不同于观测值,呈明显的U型分布,说明集合离散度偏小,不能代表实际观测的不确定性特征;而CAMS则呈L型,表明预报值偏大,使得观测值时常处于最小次序的位置,同时离散度偏小,在预报质量上则具有显著的高温预报偏差,即空报较多;NMC的U型分布也有一定的高温预报偏差。

图2 5组集合预报的850 hPa温度24 h预报的 Talagrand分布 a.NCEP;b.ZAMG;c.JMA;d.CAMS;e.NMCFig.2 Talagrand distribution for the 850-hPa 24-h temperature forecast of the five sets of ensemble forecasts:(a)NCEP;(b)ZAMG;(c)JMA;(d)CAMS;(e)NMC
2.2预报可辨识度
ROC曲线是不同检验阈值的命中率与误报率对应各点的连线,该曲线以下覆盖的面积称为ROC面积,代表集合预报区分未来不同天气事件能力的大小。理想集合预报的ROC曲线由x=0和y=1组成,对应的面积为1。对于实际的集合预报,ROC面积愈接近于1,说明该集合预报区分天气事件的能力就越好。通过对比12 h预报的850 hPa温度的ROC曲线的形态和ROC面积(图3a)可见,NCEP与ZAMG的ROC面积较大,分别达到0.94和0.95,说明二者对未来不同天气事件的区分能力较优;而JMA与NMC的ROC面积分别仅为0.89和0.80,CAMS的ROC面积更低至0.65,反映了这些集合预报相对较低的区分未来不同天气事件的能力。对于24 h预报(图3b)而言,ZAMG、NCEP和JMA的ROC面积均在0.90以上,具有同12 h预报接近的质量。NMC的则为0.83,比12 h预报略有升高,而CAMS的预报能力依然最差。从ROC面积指标来看,无论12 h还是24 h的区域集合预报,NMC和CAMS对未来不同天气事件的区分能力相对于其他三者都明显偏低。
2.3综合评分

图3 850 hPa温度集合预报的ROC评分 a.12 h预报;b.24 h预报Fig.3 ROC curves for the 850-hPa temperature forecasts of five sets of ensemble forecasts:(a)12 h;(b)24 h
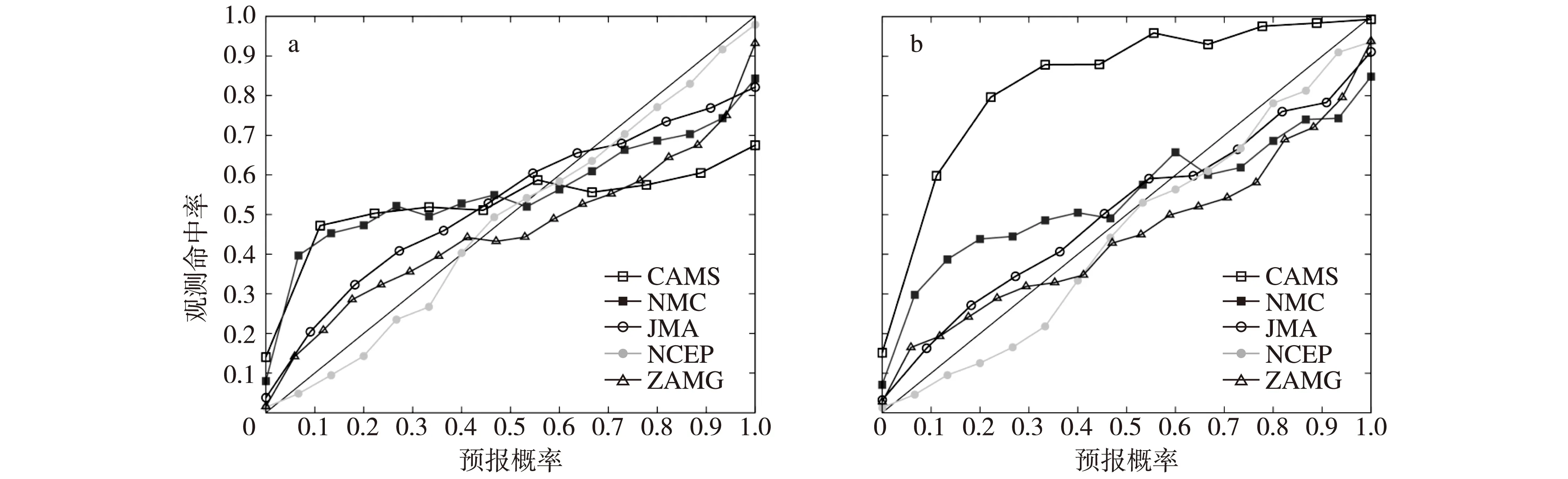
图4 850 hPa温度集合预报的可信度 a.12 h预报;b.24 h预报Fig.4 Reliability diagram for the 850-hPa temperature forecasts of five sets of ensemble forecasts:(a)12 h;(b)24 h
可信度曲线为综合评价集合预报可信度(reliability)和可辨识度(resolution)的综合反映,是通过对不同检验阈值的预报概率分类中观测事件发生的相对频率进行统计而得到的结果(Hartmann et al.,2002)。理想的预报概率与观测事件的频率相同,此时可信度曲线为x=y的对角线。从5个中心集合预报温度降温2 ℃预报的可信度曲线(图4)来看,无论12 h(图4a)还是24 h(图4b)预报,NCEP集合预报的可信度曲线总体上稳定处于对角线附近两侧,显示出较高质量的预报可信度与可辨识度,只是24 h预报中在低预报概率(0~0.4)区间的预报概率略大于观测频率,导致可辨识度略低;从JMA的可信度曲线可以发现,其24 h预报的可信度曲线分布优于12 h预报,基本上与NCEP的预报可信度和可辨识度相当。说明随着预报时间的延长,集合预报的可信度和可辨识度的变化与预报模式的性能具有重要的关系;ZAMG的可信度曲线显示,在两个预报时效内其在中高预报概率区间的预报值均偏大,且可信度曲线中间部分斜率偏小,可辨识度偏低;CAMS的可信度曲线分布明显偏离x=y的对角线,说明其在整个预报概率分布区间内的预报可辨识度均较差。尤其在24 h预报中都呈现预报概率远低于观测频率,说明其预报值显著小于实际观测值,类似的情形也出现在NMC的中低预报概率(0~0.5)区间。
3 综合偏差订正
理想集合预报的集合平均预报误差为零,集合离散度能够合理表征实际大气运动的不确定性特征。由于数值预报模式存在预报偏差,很大程度上导致了集合预报的偏差;另外,初始扰动构造方案的不尽合理也通常会造成集合离散度偏低,这都会限制集合预报的整体性能。因此,在业务应用前,一般都会对集合预报进行偏差订正和离散度的合理调整。本文采用基于卡尔曼滤波的递减平均后验订正的综合偏差订正方法(马旭林等,2015),对5套集合预报进行偏差订正,以改善其整体质量,提高应用能力。
3.1综合偏差订正方案
集合预报的综合偏差订正包括一阶矩及二阶矩订正,其中一阶矩偏差订正是订正集合平均预报偏差以增加预报可靠性,二阶矩订正通过改善集合预报概率密度函数与观测值的概率分布一致性,实现集合离散度的调整。综合偏差订正则是在一阶矩订正的基础上加入二阶矩订正,先后调整集合预报偏差和集合离散度,以改善集合预报质量。因综合偏差订正方案中的一阶矩与二阶矩偏差订正相互独立并先后进行,故单独试验的最优权重系数适用于综合偏差订正。
由于B08RDP项目资料时长的限制,试验中选取20 d的集合预报作为一阶矩和二阶矩订正的训练资料。综合偏差订正共分为两步:首先进行一阶矩偏差订正以去除集合平均预报偏差;然后使用一阶矩偏差订正后的集合平均预报误差调整集合离散度。综合偏差订正方案的详细说明请参见马旭林等(2015)文献。

图5 850 hPa温度集合预报订正前(虚线)、后(实线)的RMSE(a)和r比值(b)Fig.5 The (a)RMSE and (b)r scores for the 850-hPa temperature of five sets of ensemble forecasts without(dashed line) and with(solid line) BC
3.2综合偏差订正效果

图6 850 hPa温度24 h集合预报偏差订正前(灰色)、后(黑色)的Talagrand分布a.NCEP;b.ZAMG;c.JMA;d.CAMS;e.NMCFig.6 Talagrand distribution for the 850-hPa temperature at 24 h of five sets of ensemble forecasts without(gray bars) and with(black bars) BC:(a)NCEP;(b)ZAMG;(c)JMA;(d)CAMS;(e)NMC
图5为各中心集合预报综合订正前后850 hPa温度预报的RMSE和r的分布。各中心集合预报订正后(实线)的RMSE评分均较订正前(虚线)评分更优(图5a),说明综合偏差订正能够有效减小集合平均预报偏差。特别是,订正前集合平均预报偏差越大,其订正效果更加显著。其中,CAMS集合预报平均偏差减小134.3%,而偏差较小的NCEP集合预报也减小了8.2%。综合偏差订正后的CAMS集合平均预报偏差仍明显大于其他集合预报,这也说明若集合预报平均偏差过大,综合偏差订正也仅能起到一定程度的改善,并不能完全去除。订正后各集合预报的r曲线均位于1附近(图5b),表明综合偏差订正对集合离散度的调整效果较为明显。进一步分析可知,综合偏差订正对NCEP的集合离散度调整幅度最小,而对CAMS的调整幅度最大,这也显示出NCEP的集合预报相对于CAMS而言具有更高的质量。
由Talagrand分布(图6)可以看出,订正后各中心集合预报更趋于水平均匀分布,各次序统计值也与理想Talagrand评分(图中横直线)更加接近。ZAMG与JMA的集合预报订正前的U型分布消失,两边次序统计值减小而中间各次序统计值增加,更接近于理想Talagrand分布;CAMS的高温预报偏差基本去除,NMC的U型也消失,高温预报偏差也基本去除。由于NCEP集合预报订正前的Talagrand分布较较为合理,订正后的调整并不显著。综上,综合偏差订正对于集合预报离散度的调整以及预报偏差的消除都具有较为明显的效果。
对比综合偏差订正前(虚线)后(实线)各中心850 hPa温度预报降温2 ℃时的ROC评分(图7)可以看出,综合偏差订正后,各集合预报的ROC面积均有不同程度的增加,表明综合偏差订正对于集合预报可辨识度的正向调整作用显著。尽管订正后各中心集合预报的ROC面积仍然差异较大,这很大程度上与订正前集合预报的质量不同有直接关系。其中订正效果最明显的为CAMS的集合预报,其12 h和24 h降温预报的ROC面积增长幅度分别达到33.8%(图7a)与29.4%(图7b),而对于订正前ROC面积较优的JMA、NCEP与ZAMG,订正后的ROC面积增长幅度则相对较小。也就是说,对于质量较差的集合预报,综合偏差订正的效果尤佳。
图8显示,12 h(图8a)和24 h(图8b)的CAMS和NMC的集合预报订正后的可信度曲线明显更接近对角线,较订正前预报值偏小的情况得到了明显改善,其中24 h的NMC集合预报,订正前中低预报概率(0~0.6)事件的预报值偏大的情况在订正后也得到了一定得缓解;同样地,订正后的NCEP、ZAMG与JMA集合预报的可信度曲线均更靠近对角线,其预报可信度和可辨识度均有不同程度的提高。

图7 850 hPa温度集合预报偏差订正前(虚线)后(实线)的ROC评分 a.12 h预报;b.24 h预报Fig.7 ROC curves for the 850-hPa temperature of five sets of ensemble forecasts without(dashed line) and with(solid line) BC:(a)12 h;(b)24 h

图8 850 hPa温度集合预报偏差订正前(虚线)后(实线)的可信度评分 a.12 h预报;b.24 h预报Fig.8 Reliability diagrams for the 850-hPa temperature of five sets of ensemble forecasts without(dashed line) and with(solid line) BC:(a)12 h;(b)24 h
综上,综合偏差订正不仅可以减小集合平均预报偏差,而且还能有效地调整集合离散度,进而改善集合预报的可信度与可辨识度,综合提高了集合预报的整体质量。值得注意的是,综合偏差订正对于质量较好的NCEP区域集合预报的订正效果较小(特别是离散度的调整),而对预报质量欠佳的CAMS和NMC集合预报的订正效果则较为明显,尤其是集合平均预报偏差的订正更加有效;对于ZAMG与JMA两套资料而言,综合偏差订正对其集合离散度和预报可辨识度的调整效果均较显著。
4 结论
本文从多个角度评估分析了B08RDP项目中5套集合预报的质量,在此基础上采用综合偏差订正方法进行综合偏差订正,并对其效果进行了讨论。
1)5套B08RDP集合预报资料中,NCEP集合预报的平均预报偏差最小,离散度最为合理,预报可信度以及可辨识度均较好,整体预报质量为最高;CAMS集合预报存在的预报偏差明显偏大,整体性能最弱,这应该与数值预报模式的性能有一定的关系;
2)从整体上看,集合离散度偏小是除NCEP之外的4套集合预报普遍存在的问题;
3)综合偏差订正方法能够有效地减小各集合预报的集合平均偏差,集合离散度的质量也有明显提高,较好地改善了离散度普遍偏小的问题,显示出综合偏差订正方法具有改善集合预报整体质量的良好能力。
References)
Alexander K,Christoph W,Yong W,et al.,2009.Calibrating 2-m temperature of limited-area ensemble forecasts using high-resolution analysis[J].Mon Wea Rev,137(10):3373-3387.
Bakhshaii A,Stull R,2009.Deterministic ensemble forecasts using gene-expression programming[J].Wea Forecasting,24(5):1431-1451.
Bowler N E,Mylne K R,Robertson K B,et al.,2009.The MOGREPS short-range ensemble prediction system[J].Quart J Roy Meteor Soc,134(632):703-722.
Charron M,Pellerin G,Spacek L,et al.,2010.Toward random sampling of model error in the Canadian ensemble prediction system[J].Mon Wea Rev,138(5):1877-1901.
陈德辉,薛纪善,杨学胜,等,2008.GRAPES新一代全球/区域多尺度统一数值预报模式总体设计研究[J].科学通报,53(20):2396-2407.Chen D H,Xue J S,Yang X S,et al.,2008.New generation of multi-scale NWP system GRAPES:General scientific design[J].Chinese Science Bulletin,53(20):2396-2407.(in Chinese).
Cui B,Toth Z,Zhu Y,et al.,2006.The trade-off in bias correction between using the latest analysis/modeling system with a short,versus an older system with a long archive[C]//The First THORPEX International Science Symposium.Montreal,Canada,World Meteorological Organization:281-284.
Cui B,Toth Z,Zhu Y,et al.,2012.Bias correction for global ensemble forecast[J].Wea Forecasting,27(2):396-410.
崔慧慧,智协飞,2013.基于TIGGE资料的地面气温延伸期多模式集成预报[J].大气科学学报,36(2):165-173.Cui H H,Zhi X F,2013.Multi-model ensemble forecasts of surface air temperature in the extended range using the TIGGE dataset[J].Trans Atmos Sci,36(2):165-173.(in Chinese).
杜钧,2002.集合预报的现状和前景[J].应用气象学报,13(1):16-28.Du J,2002.Present situation and prospects of ensemble numerical prediction[J].J Appl Meteor Sci,13(1):16-28.(in Chinese).
Du J,Dimego G,Tracton M S,et al.,2003.NCEP short-range ensemble forecasting(SREF) system:Multi-IC,multi-model and multi-physics approach[C]//Research Activities in Atmospheric and Oceanic Modeling.Washington:NCEP.
Du J,McQueen J,DiMego G,et al.,2006.New dimension of NCEP SREF system:Inclusion of WRF members[R]//Report to WMO Export Team Meeting on Ensemble Prediction System.Exeter,UK:WMO.
Du J,Dimego G,Toth Z,2007.Bias correction for the SREF at NCEP and beyond[C]//A discussion at the EMC Predictability Meeting.Washington:EMC.
Duan Y,Gong J,Du J,et al.,2012.An overview of the Beijing 2008 Olympics research and development project(B08RDP)[J].Bull Amer Meteor Soc,93(3):381-403.
Gneiting T,Raftery A E,Westyeld A H,et al.,2005.Calibrated probabilistic forecasting using ensemble model output statistics and minimum CRPS estimation[J].Mon Wea Rev,133(5):1098-1118.
Hartmann H C,Pagano T C,Sorooshiam S,et al.,2002.Confidence builder:Evaluating seasonal climate forecasts from user perspectives[J].Bull Amer Met Soc,83(5):683-698.
Johnson C,Swinbank R,2009.Medium-range multi-model ensemble combination and calibration[J].Quart J Roy Meteor Soc,135(640):777-794.
Krishnamurti T N,Gnanaseelan C,Chakraborty A,2007.Prediction of the diurnal change using a multimodel superensemble.Part I:Precipitation[J].Mon Wea Rev,135(10):3613-3632.
李莉,李应林,田华,等,2011.T213全球集合预报系统性误差订正研究[J].气象,37(1):31-38.Li L,Li Y L,T H,et al.,2011.Study of bias-correction in T213 global ensemble forecast[J].Meteor Mon,37(1):31-38.(in Chinese).
Li X,Charron M,Spacek L,et al.,2008.A regional ensemble prediction system based on moist targeted singular vectors and stochastic parameter perturbations[J].Mon Wea Rev,136(2):443-462.
麻巨慧,朱跃建,王盘兴,等,2011.NCEP、ECMWF及CMC全球集合预报业务系统发展综述[J].大气科学学报,34(3):370-380.Ma J H,Zhu Y J,Wang P X,et al.,2011.A review on the developments of NCEP,ECMWF and CMC global ensemble forecast system[J].Trans Atmos Sci,34(3):370-380.(in Chinese).
马旭林,薛纪善,陆维松,2008.GRAPES全球集合预报的集合卡尔曼变换初始扰动方案初步研究[J].气象学报,66(4):526-536.Ma X L,Xue J S,Lu W S,2008.Preliminary study on ensemble transform Kalman filter-based initial perturbation scheme in GRAPES global ensemble prediction[J].Acta Meteorologica Sinica,66(4):526-536.(in Chinese).
马旭林,庄照荣,薛纪善,等,2009.GRAPES非静力数值预报模式的三维变分资料同化系统的发展[J].气象学报,67(1):50-60.Ma X L,Zhuang Z R,Xue J S,et al.,2009.Development of 3D Variational data assimilation system for the nonhydrostatic numerical weather prediction model-GRAPES[J].Acta Meteorologica Sinica,67(1):50-60.(in Chinese).
Ma X,Xue J,Lu W,2009.Study on ETKF-based initial perturbation scheme for GRAPES global ensemble prediction[J].Acta Meteorologica Sinica,23(5):562-574.
马旭林,陆续,于月明,等,2014.数值天气预报中集合-变分混合资料同化及其研究进展[J].热带气象学报,30(6):1188-1195.Ma X L,Lu X,Yu Y M,et al.,2014.Progress on hybrid ensemble-variational data assimilation in numerical weather prediction[J].J Trop Meteor,30(6):1188-1195.(in Chinese).
马旭林,时洋,和杰,等,2015.基于卡尔曼滤波递减平均算法的集合预报综合偏差订正[J].气象学报,73(5):952-964.Ma X L,Shi Y,He J,et al.,2015.The combined descending averaging bias correction based on the Kalman filter ensemble forecast[J].Acta Meteorologica Sinica,73(5):952-964.(in Chinese).
Marsigli C,Montani A,Paccagnella T,2008.A spatial verification method applied to the evaluation of high-resolution ensemble forecasts[J].Meteorol Appl,15(1):125-143.
Raftery A E,Gneiting T,Balabdaoui F,et al.,2005.Using Bayesian model averaging to calibrate forecast ensembles[J].Mon Wea Rev,133(5):1155-1174.
Saito K,Fujita T,Yamada Y,et al.,2006.The operational JMA nonhydrostatic mesoscale model[J].Mon Wea Rev,134(4):1266-1298.
Toth Z,Talagrand O,Candille G,et al.,2003.Probability and ensemble forecasts.Forecast verification:A practitioner’s guide in atmospheric science[R]//John Wiley and Sons.
Wang X,Bishop C H,2003.A comparison of breeding and ensemble transform Kalman filter ensemble forecast schemes[J].J Atmos Sci,60(9):1140-1158.
Wang Y,Bellus M,Geleyn J,et al.,2014.A new method for generating initial condition perturbations in a regional ensemble prediction system:Blending[J].Mon Wea Rev,142(5):2043-2059.
Wang Y,Bellus M,Wittmann C,et al.,2011.The central European limited-area ensemble forecasting system:ALADIN-LAEF[J].Quart J Roy Meteor Soc,137(655):483-502.
Wang Y,Kann A,Bellus M,et al.,2010.A strategy for perturbing surface initial conditions in LAMEPS[J].Atmos Sci Lett,11(2):108-113.
Wilks D S,2006.Statistical methods in the atmospheric sciences[M].San Diego:Academic Press of Elsevier:255-336.
智协飞,季晓东,张璟,等,2013.基于TIGGE资料的地面气温和降水的多模式集成预报[J].大气科学学报,36(3):257-266.Zhi X F,Ji X D,Zhang J,et al.,2013.Multimodel ensemble forecasts of surface air temperature and precipitation using TIGGE datasets[J].Trans Atmos Sci,36(3):257-266.(in Chinese).
智协飞,李刚,彭婷,2014a.基于贝叶斯理论的单站地面气温的概率预报研究[J].大气科学学报,37(6):740-748.Zhi X F,Li G,Peng T,2014a.On the probabilistic forecast of 2 meter temperature of a single station based on Bayesian theory [J].Trans Atmos Sci,37(6):740-748.(in Chinese).
智协飞,彭婷,李刚,等,2014b.多模式集成的概率天气预报和气候预测研究进展[J].大气科学学报,37(2):248-256.Zhi X F,Peng T,Li G,et al.,2014b.Advances in multi-model ensemble probabilistic prediction[J].Trans Atmos Sci,37(2):248-256.(in Chinese).
Five sets of regional ensemble forecasts with lead times of 36 h over two months from 24 June 2008 to 24 August 2008 from the Beijing 2008 Olympics Research and Development Project(B08RDP) are evaluated and analyzed.This is firstly done by means of standard probabilistic verification scores,including root-mean-square error(RMSE),ensemble spread,talagrand diagrams,reliability,and ROC(Relative Operating Characteristic) curves.Then,to improve the forecast quality,a combined decaying averaging bias correction scheme(BC) is applied to the ensemble forecasts of B08RDP to reduce the bias in the ensemble mean and to adjust the improper spread of ensembles with sufficient performance evaluation.The BC scheme is designed based on the original Kalman filter.It contains the first moment bias correction,mainly for correcting the bias in the ensemble mean to improve the reliability of the ensemble forecasts,and the second moment bias correction mainly for adjusting the ensemble spread to make the ensemble forecasts fully representative of the uncertainties in the observations.Lastly,the BC scheme’s capacity is evaluated and discussed by means of the verification scores mentioned above.Temperatures at 850 hPa are corrected and verified in this study,wherein ECMWF reanalysis data are used as the reference for the verification.
The results show that,among the five sets of regional ensemble forecasts in B08RDP,the regional ensemble forecasts from NCEP possess the best forecast quality,with minimal bias,the most appropriate spread,and the best performance in terms of reliability,resolution and talagrand distributions.Meanwhile,the regional ensemble forecast from CAMS demonstrates the worst forecast quality,due to its largest forecast bias.On the whole,a relatively small spread is a common problem for several of the ensemble forecasts,except those from NCEP.In general,the combined bias correction scheme is proven to be efficient in reducing the RMSE of the ensemble mean,and in generating a more appropriate ensemble spread,for the five sets of ensemble forecasts,revealing its ability to improve the quality of ensemble forecasts,especially for ensemble forecasts of an already low quality.
numerical weather prediction;ensemble weather forecast;combined bias correction;performance evaluation;B08RDP
(责任编辑:孙宁)
Evaluation and combined bias correction on temperature forecast of regional ensemble prediction system of B08RDP
MA Xulin1,ZHOU Boyang1,SHI Yang1,2,JI Yanxia1,He Jie1
1KeyLaboratoryofMeteorologicalDisaster,MinistryofEducation(KLME),NanjingUniversityofInformationScience&Technology,Nanjing210044,China;2GuangdongMeteorologicalObservatory,Guangzhou510080,China
10.13878/j.cnki.dqkxxb.20141124003
引用格式:马旭林,周勃旸,时洋,等,2016.B08RDP区域集合预报温度场质量评估与综合偏差订正[J].大气科学学报,39(5):643-652.
Ma X L,Zhou B Y,Shi Y,et al.,2016.Evaluation and combined bias correction on temperature forecast of regional ensemble prediction system of B08RDP[J].Trans Atmos Sci,39(5):643-652.doi:10.13878/j.cnki.dqkxxb.20141124003.(in Chinese).
*联系人,E-mail:xulinma@nuist.edu.cn

