NGB-W广播信道估计实现算法设计

陈　健，唐　杰，李明齐

(1.中国科学院上海高等研究院，上海 200120；2.中国科学院大学，北京 100049；3.上海科技大学，上海 200120)



NGB-W广播信道估计实现算法设计

陈健1,2,3，唐杰1,2,3，李明齐1

(1.中国科学院上海高等研究院，上海 200120；2.中国科学院大学，北京 100049；3.上海科技大学，上海 200120)

针对下一代广播电视网无线系统(NGB-W)广播接收信道估计，提出了一种基于二次一维维纳滤波的信道估计实用算法。该算法实时估计信道多普勒频偏、时延扩展和噪声方差等参数，并根据参数估计值分别从离线获得的预选集中选择时域和频域的一维维纳滤波系数。通过Cocentric System Studio(CCSS)平台仿真，给出了参数估计对算法性能的影响，以及所提信道估计算法的均方误差和误块率性能。仿真结果表明该算法在不同移动速度下，与采用理想插值系数信道估计相比性能损失不超过0.4 dB，与理想信道估计相比性能损失在1 dB以内。

信道估计；维纳滤波；下一代无线广播网；参数估计

作为国家信息基础设施建设的重要战略，我国中长期规划纲要中明确指出应积极推进电信网、广播电视网和互联网的三网融合[1]。为应对三网融合国家战略，广电提出了下一代广播电视网(NGB)[2]解决方案。下一代广播电视无线网(NGB-W)作为NGB总体构架的重要组成部分，广播与双向融合的NGB-W系统可以进一步提升广电无线网络全业务支撑的能力[3]。

NGB-W广播信道采用正交频分复用(OFDM)技术[4]。为了使NGB-W广播接收机能够在无线信道环境下有效解调接收信号，在接收端选择合适的信道估计算法来恢复出原始的数据流就显得十分重要。信道估计算法根据是否使用辅助信息可以分为基于导频的信道估计、半盲或盲估计。尽管前者在数据中插入导频会占用系统的带宽从而降低有效数据的传输速率，但与后者相比，可获得更鲁棒的接收机性能，因此一般的应用场景大多采用该类算法[5]。在基于导频的信道估计算法中，维纳滤波信道估计算法是一种估计性能较好的算法。二维的维纳滤波算法实现复杂度较高，为了降低复杂度，文献[6-7]提出分别在时域和频域进行一维维纳滤波，在此基础上文献[5]提出根据特定场景下的信道参数离线产生维纳滤波插值系数，在信道估计时直接调用，文献[8]提出按噪声方差分区非实时地计算插值系数，在信道估计时根据噪声方差估计值选取对应的插值系数。但在实际系统中无线移动信道的传播环境十分恶劣，信道的噪声、不同移动速度下的多普勒频移和多径传播引起的时延扩展都会对系统性能有较大影响。

因此，本文针对NGB-W广播接收机信道估计，提出采用参数估计算法分别估计信道多普勒频移、时延扩展和噪声方差，按区间划分离线产生的时频域插值系数，信道估计算法通过信道参数估计值实时地选取对应区间内的插值系数。通过基于Cocentric System Studio(CCSS)平台的仿真，给出了不同信道环境下所提各参数估计方法分别对系统性能的影响，以及基于所提参数估计和分区方法的二次一维维纳滤波信道估计算法的系统性能仿真结果。仿真结果表明，使用参数估计方法能区分出不同的信道环境，确保信道估计算法在变化的信道环境下正常工作。

1　系统模型

NGB-W广播的单发单收(SISO)物理层框架如图1所示。

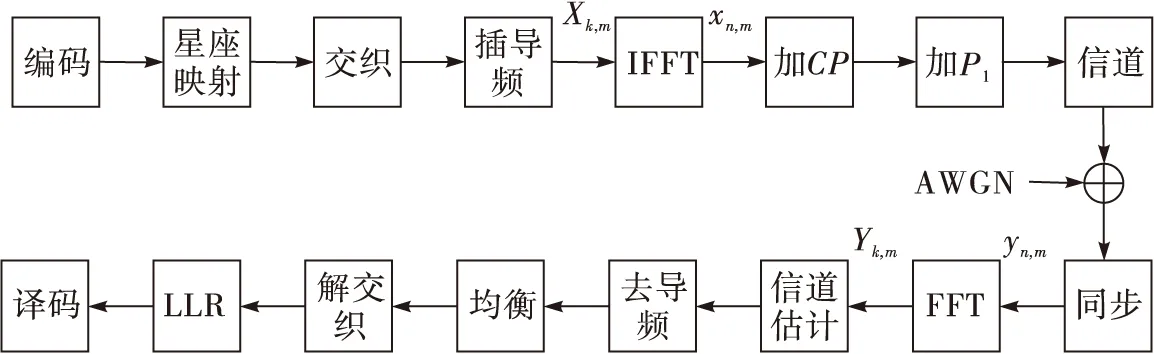
图1　NGB-W广播系统模型

在发射端首先产生成帧的数据，然后插入导频。通过快速傅里叶逆变换(IFFT)模块把插完导频后的第m个OFDM符号从频域变换到时域

(1)

式中：N代表子载波个数。

NGB-W广播接收机由一系列与发端相反的操作过程组成，将天线接收下来的第m个OFDM符号第n个样点yn,m经过FFT模块得到频域第k个子载波信号

(2)

假设信道时延小于保护间隔且信道在一个OFDM符号之内不变，同时接收端定时同步无误差，则接收信号Yk,m和发射信号Xk,m之间的关系可以表示为

Yk,m=Hk,mXk,m+Wk,m

(3)

其中：Wk,m是第m个OFDM符号第k个子载波的AWGN噪声。因此，要从接收信号中采用相干检测恢复出原始信号，就需要在接收端采用信道估计算法来估计出信号所经过的信道Hk,m。

NGB-W系统中每帧信号包括一个前导符号P1和若干数据符号。P1符号可用于估计信道时延，在数据符号中插入的导频用于信道估计。NGB-W广播信道协议定义了不同的导频插值方式，使得系统能够适应不同的信道环境。图2为本文中使用的导频结构。图中，k=1和k=3 098处的导频为连续导频，其余为离散导频。

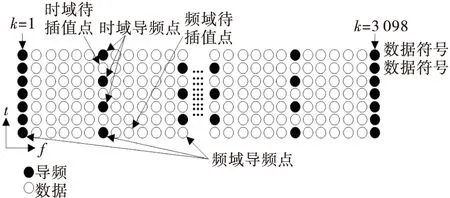
图2　NGB-W广播导频结构

2　维纳滤波信道估计实现算法

2.1二次一维维纳滤波

二次一维维纳滤波信道估计算法的具体实现方式如图3所示。维纳滤波所需的关键参数，如时延扩展、多普勒频偏和噪声方差都需要实时估计。为了降低广播接收机实现的复杂度，在进行时域、频域插值时，分别根据信道多普勒频移、时延扩展和噪声方差可能的取值范围将其划分为几个区间，每一个区间预先计算出一组与之相应的插值系数。通过估计得到的信道参数，选择对应区间内的系数作为此次维纳滤波插值系数。

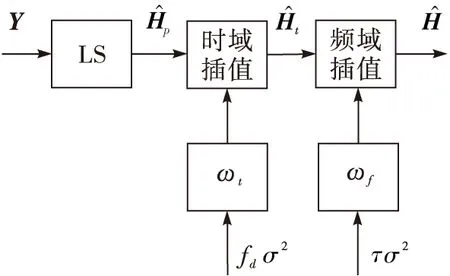
图3　信道估计算法框图

2.1.1导频LS信道估计

首先根据LS估计算法得到所有导频位置上的信道估计值

(4)

其中：Xp是在信号中插入的频域导频值；Yp是接收到的OFDM符号中导频位置的信号。之后分别通过时域和频域一维维纳滤波对数据子载波信道进行插值。

2.1.2时域一维维纳滤波插值信道估计

对LS算法得到的信道频率响应值H^p先进行时域插值。利用导频处已经得到的值估计时域相邻位置处的信道值，如图2中所示。时域插值公式

H^t=ωtH^p

(5)

ωt=Rt_hp(Rt_pp+σ2I)-1

(6)

其中：Rt_hp表示数据子载波与导频子载波的时域互相关矩阵；Rt_pp表示导频子载波的时域自相关矩阵；σ2表示AWGN信道的噪声方差；I是单位矩阵。时域相关矩阵Rt_hp和Rt_pp中的系数计算通过公式求得

Rt=J0(2πfdΔt)

(7)

其中：J0为第一类零阶贝塞尔函数；fd为信道多普勒频偏；Δt为某个系数对应的子载波之间的时域间隔。

2.1.3频域一维维纳滤波插值信道估计

时域插值完成之后，在每个OFDM符号中利用已估计得到信道值H^t进行频域插值，如图2所示。频域插值公式

H^f=ωfH^t

(8)

ωf=Rf_hp(Rf_pp+σ2I)-1

(9)

其中：Rf_hp表示频域维数据子载波与导频子载波间的互相关矩阵；Rf_pp表示频域维导频子载波间的自相关矩阵。频域维相关矩阵的系数计算公式

(10)

其中：τ为信道最大时延扩展；τrms为信道的均方时延扩展；N为OFDM符号的FFT长度；k为频域维上的子载波间隔。

2.2时延扩展估计

时延扩展的估计步骤为：

1)假设理想时频同步。从接收的数据中分离出长度为NP1的P1符号，并由P1符号获得信道冲击响应估计值h^n,n=1,2，…,NP1。

2)在h^n中搜索能量最大的能量窗位置

(11)

其中：M为搜索能量窗大小。

3)设定能量窗内搜索最前端和最后端径的门限值Th1和Th2分别为

(12)

(13)

4)搜索能量窗内最前端径的位置

pos2=pos1+offsetf

(14)

其中：offsetf等于满足下式的第一个i值

(15)

5)搜索能量窗内最后端径的位置

pos3=pos1+M-1-offsetb

(16)

其中：offsetb等于满足下式的第一个i值

(17)

6)计算信道时延扩展估计值为

τ=pos3-pos2

(18)

2.3多普勒频偏估计

多普勒频偏估计步骤为：

1)对L个OFDM符号的第l个连续导频位置处信道估计值H^l,m做DFT，获得H^l,m的功率谱

(19)

2)获得单边功率谱边缘位置

(20)

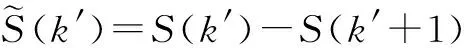
(21)

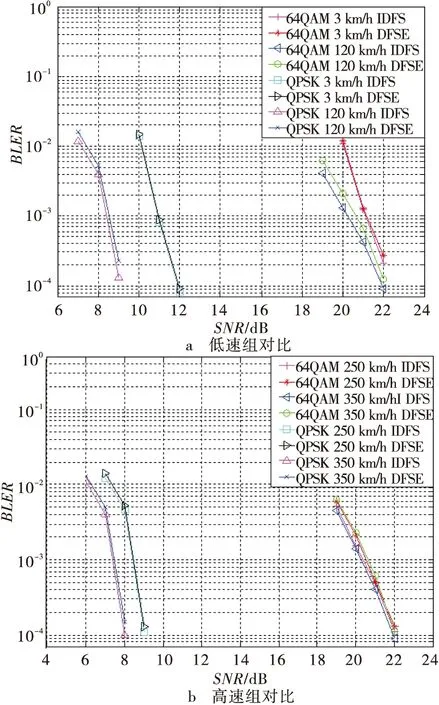
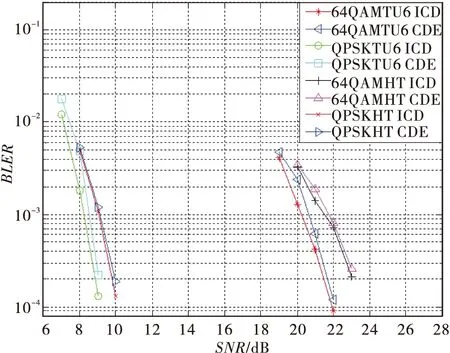
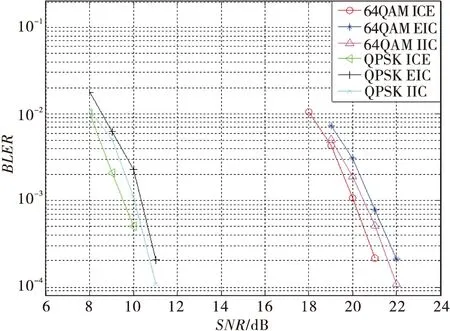
st.S(k′+1)

(22)

Ths为确保取到边缘位置而设置的门限，其值的选取受信道特性的影响，可根据下式计算

(23)

其中：C为常数。

3)根据频谱宽度估计信道多普勒频偏

(24)

其中：Δt为一个OFDM符号时域长度。

2.4噪声方差估计

利用导频值和导频子载波的信道估计值，可得噪声方差的估计值为

(25)

其中：H^fpi,j是通过等式(8)计算得到的频域插值后第j个OFDM符号中第i个导频子载波信道估计值；J是一个符号中导频子载波的总数。

2.5插值系数选择

根据在不同的信道环境下的不同信道参数(多普勒频移、时延扩展和噪声方差)对应的系数对系统性能的遍历仿真分析，确定信道参数的区间以及对应的插值系数。一般情况下，插值系数对应信道参数区间的中值。离线生成的各组插值系数储存在接收机本地。

接收机信道估计时，根据信道参数的估计值选择相应的参数区间对应的插值系数，实现维纳滤波算法。上述方法解决了信道估计算法实现复杂度和实时性之间的矛盾。显然，系数区间划分得越细，插值结果越接近理想参数的信道值，但所需系数占用存储空间也越多。实际应用中应在满足系统性能要求的情况下，尽量减少系数的分区数。

3　仿真结果及分析

本文使用Synopsys公司的基于SystemC系统的开发和模拟工具CCSS搭建NGB-W仿真平台。CCSS采用流式驱动的方法，使仿真系统构成更接近于硬件实现系统。

NGB-W广播系统仿真采用载波频率700 MHz，采样频率10 MHz，FFT长度为4 096，保护间隔为1/8，采用LDPC编码，1/2码率，QPSK、64QAM调制方式。在TU6、HT信道下对系统进行了仿真，为验证信道估计的性能，假设理想时频同步。

噪声方差取值分成2个区间：[0，0.02)，[0.02，+∞)，维纳滤波系数取值分别对应信噪比在20 dB和10 dB时的值。信道时延取值分成6个区间：[0，16)，[16，32)，[32，64)，[64，128)，[128，256)，[256，+∞)，维纳滤波系数取值分别对应区间中间值计算得到的频域插值系数。信道多普勒频偏估计采用64个OFDM符号，由式(19)可知，频率分辨率约为33.9 Hz。多普勒频偏取值分成4个区间：[0，100)，[100，160)，[160，+∞)，维纳滤波系数取值分别对应移动速度100 km/h，200 km/h和300 km/h时域固定插值系数。

图4～6分别给出了按照所提的多普勒频偏、时延扩展和噪声方差参数估计方法实时地选择插值系数与理想插值系数进行信道估计的性能对比。仿真表明，根据参数估计结果(多普勒频偏估计(DFSE)、噪声方差(NVE)、信道时延(CDE))选取插值系数的系统性能与使用理想参数选取(理想多普勒频偏估计(IDFS)、理想噪声方差(INV)、理想信道时延(ICD))对应的插值系数的系统性能十分接近，性能损失在0.2 dB以内。

图4　TU6信道下多普勒频偏(DFS)估计对性能的影响

图5　TU6-120 km/h、HT-120 km/h信道下信道时延(CD)估计对性能的影响

图6　TU6-120 km/h信道下噪声方差(NV)估计对性能的影响

图7给出了在TU6-120km/h信道下，采用实时估计信道参数来选择插值系数算法的均方误差(MSE)和使用理想插值系数算法的均方误差对比结果。由图可见，在低信噪比区域，两者性能差异小于1dB，在高信噪比区域，两者差异逐渐扩大，且均出现MSE平层，可以预见将对高阶调制的接收性能产生影响。

图7　均方误差性能比较

图8～9分别给出了TU6信道不同移动速度下，估计插值系数(EIC)和理想插值系数(IIC)、理想信道估计(ICE)的误块率性能比较。由图可见，按照所提参数估计方法在不同移动速度下性能都接近采用理想插值系数信道估计的方式，损失不超过0.4dB，与理想信道估计相比，损失在1dB以内。

图8　TU6-30 km/h信道下的性能比较

图9　TU6-350 km/h信道下的性能比较

4　结束语

本文针对NGB-W广播接收信道估计实用算法设计，给出时频二次一维维纳滤波系数实时选择所需的多普勒频移、时延扩展和噪声方差参数估计方法。基于给定的参数区间，通过采用CCSS的仿真表明，根据各参数估计结果选取插值系数的信道估计性能与使用理想系数的性能相比，最大性能损失在0.4dB以内，与理想信道估计相比，损失在1dB以内。

[1]封松林，解伟.下一代广播电视网无线系统[J].中兴通讯技术，2011，17(4)：14-18.

[2]KOUYJ，RUIY.Nextgenerationbroadcastwirelesssystems：challengsandtrends[C]//Proc.CommunicationWorkshop(ICCW).London：IEEE，2015：2604-2609.

[3]ZHANGWJ，HEDZ，GUANYF，etal.BriefintroductiononthekeytechnologiesofNGB-Wbroadcastingchannel[C]//Proc.BroadbandMultimediaSystemsandBroadcasting(BMSB).Ghent：IEEE， 2015：1-9.

[4]王联.NGB-W系统综述[J]. 电视技术，2014，38(17)：13-17.

[5]芮赟，李明齐，张小东，等.一种有效降低复杂度的2×1D维纳滤波信道估计方法[J]. 电视技术，2008，48(5)：27-31

[6]HOHERP.TCMonfrequency-selectiveland-mobilefadingchannels[C]//ProcTirreniaIntWorkshopDigitalCommunications.Tirrenia，Italy：IEEE，1991：317-328.

[7]PETERH，STEFANK，PATRICKR.Pilot-symbol-aidedchannelestimationintimeandfrequency[C]//Proc.CommunicationTheoryMini-Conference(CTMC)withinIEEEGlobalTelecommunicationsConference.Phoenix，USA：IEEE，1997：90-96.

[8]刘春娟，钱良. 基于维纳滤波的二维联合信道估计的实现[J]. 信息技术，2008 (5)：27-39.

陈健，硕士研究生，主研无线三网融合；

唐杰，博士研究生，主研无线三网融合；

李明齐，博士生导师，为本文通信作者，主要研究方向为三网融合，基于GPP的软件无线电。

责任编辑：闫雯雯

Design of channel estimation realization algorithm in the Next Generation Broadcast Wireless

CHEN Jian1,2,3，TANG Jie1,2,3， LI Mingqi1

(1.ShanghaiAdvancedResearchInstitute，ChineseAcademyofSciences,Shanghai200120,China； 2.UniversityofChineseAcademyofSciences，Beijing100049,China； 3.ShanghaitechUniversity,Shanghai200120,China)

The channel estimation in the next generation broadcast wireless(NGB-W) system is studied， and a channel estimation practical algorithm based on 2×1_D Wiener filter is proposed. The proposed algorithm estimates channel doper frequency， delay expansion and noise variance in real-time， and chooses 1_D Wiener filter coefficients from the pre selected set which is calculated off-line according to channel parameter estimated values. From the Cocentric System Studio(CCSS) simulation results， the influence of the parameters estimation to the channel estimation algorithm is got. Furthermore， the mean square error and block error rate of the channel estimation algorithm are got. Simulation results show that the proposed algorithm losses performance in 0.4 dB compare to channel estimation which use ideal wiener filter coefficients and losses performance in 1 dB compare to ideal channel estimation.

channel estimation； Wiener filter； Next Generation Broadcast-Wireless(NGB-W)； parameter estimation

TN934

ADOI： 10.16280/j.videoe.2016.10.026

上海市科委项目(145111011305)；中科院先导科技专项(XDA06010300)

2016-02-22

文献引用格式：陈健，唐杰，李明齐. NGB-W广播信道估计实现算法设计[J].电视技术，2016，40(10)：131-136.

CHEN J，TANG J， LI M Q. Design of channel estimation realization algorithm in the Next Generation Broadcast Wireless[J]. Video engineering，2016，40(10):131-136.