基于核空间马尔科夫随机场的图像模糊聚类

屈汉章, 徐　丹, 吴成茂

(1. 西安邮电大学 理学院， 陕西 西安 710121；　2. 西安邮电大学 通信与信息工程学院， 陕西 西安 710121;3. 西安邮电大学 电子工程学院， 陕西 西安 710121)



基于核空间马尔科夫随机场的图像模糊聚类

屈汉章1, 徐丹2, 吴成茂3

(1. 西安邮电大学 理学院， 陕西 西安 710121；2. 西安邮电大学 通信与信息工程学院， 陕西 西安 710121;3. 西安邮电大学 电子工程学院， 陕西 西安 710121)

引入核函数，对马尔科夫随机场图像模糊聚类算法加以改进，即利用核函数把马尔科夫随机场的输入空间信息样本映射到高维特征空间，在特征空间完成聚类。对标准灰度图像添加高斯噪声和椒盐噪声，利用改进算法实现聚类，视觉效果及分割图像的峰值信噪比显示，改进算法的聚类能力、分类精度和抗噪性能均有提高。

模糊C-均值聚类；核函数；马尔科夫随机场；空间信息

模糊聚类算法是实现图像分割的基本方法之一[1-3]。模糊C-均值(Fuzzy C-means, FCM)聚类[4-5]对无噪图像分割有效，但因忽略了空间信息，故对图像噪声和成像伪影非常敏感。对其目标函数加入像素邻域信息约束，可得邻域信息约束的FCM聚类分割法[6]，但需计算像素及其邻域像素到类中心的距离，复杂性较高，实时性差。

针对FCM聚类的改进算法中，基于核函数的FCM(Kernel-based FCM, KFCM)聚类算法[7-10],将输入模式空间映射到高维空间中，以使非线性信息转换为线性问题。基于马尔科夫随机场的FCM(Markov Random Field based FCM, MRFFCM)聚类算法[11-13],作为一种新的结合空间信息的FCM算法，通过引入新模糊因子，并将空间信息和灰度信息相融合，来改善算法对噪声的鲁棒性，但当噪声较大时，其分割准确性依然较低，且计算复杂度高，不适合大幅面遥感和医学图像分割。

本文拟将KFCM聚类算法和MRFFCM聚类算法相结合，给出一种基于核空间的MRFFCM分割改进算法，以求提高抗噪性能，使其适用干扰环境图像分割。

1　两种聚类算法

1.1KFCM聚类算法

KFCM聚类算法通过构造新特征向量，将输入模式空间映射到高维特征空间，从而使原空间的非线性信息转换为线性信息。其目标函数为[10]21-22

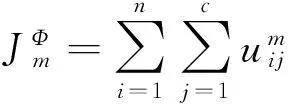
其中m是加权指数(一般取值为2)，Φ指特征映射。根据核函数的转换方法，有

‖Φ(xi)-Φ(vj)‖2=

[Φ(xi)-Φ(vj)]T[Φ(xi)-Φ(vj)]=

[Φ(xi)]TΦ(xi)-[Φ(vj)]TΦ(vj)-

[Φ(xi)]TΦ(vj)+[Φ(xi)]TΦ(vj)=

K(xi,xi)K(vj,vj)-2K(xi,vj)。

核函数的选取应满足Mercer条件[14]，故取高斯核函数，即

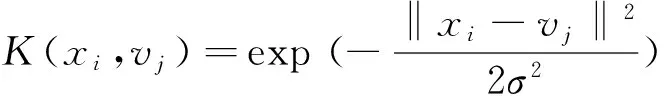
由此可得

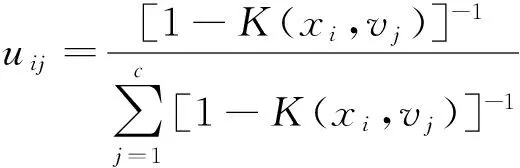
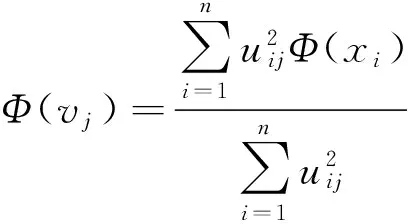
KFCM聚类算法可以较好地分辨、提取和放大有用特征，更准确地实现聚类，同时算法收敛速度也较好。

1.2MRFFCM聚类算法

MRFFCM聚类算法，通过引入MRF空间各像素的位置来改进FCM算法，图像各像素只与其邻域像素相关，与邻域外像素无关，只要给出图像的先验局部结构信息，就能得到更好的分割精度。像素点的属性仅与其邻域相关，而与其他区域无关时，称其具有随机字段马尔科夫性。

MRFFCM聚类算法的目标函数为[13]100-101

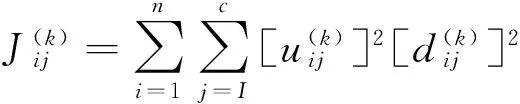
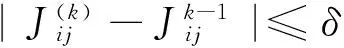
MRFFCM聚类算法的局部空间约束能力有限，而图像信息又具有很强随机性，因此，该算法虽然具有一定抗噪性能，但对于强噪声，分割准确性仍然比较低。

2　改进算法

核函数可以避免“维数灾难”，减小计算量，而输入空间的维数n对核函数矩阵无影响，引入核函数可以有效处理高维输入。将核空间和MRFFCM算法相结合，能更有效地进行图像分割。

改进算法的目标函数设定为

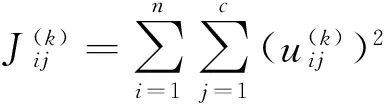
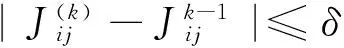
2.1能量函数

改进算法选取能量函数

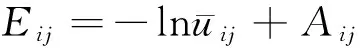
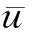
Aij=tijβjnij。

其中,tij是调整项符号，代表一个数，以决定第j类中像素xi为中心像素点，βj是人工参数，nij意为第j类中像素xi邻域系统的样本数。

2.2随机场局部概率

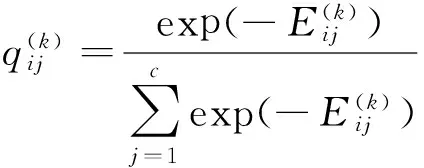
再计算条件概率

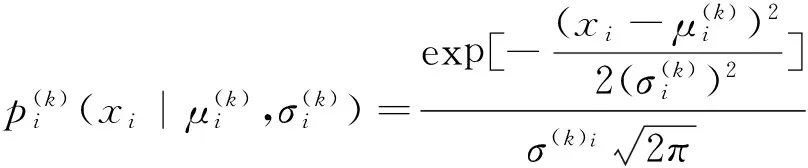
进而得出样本xi到vj的距离

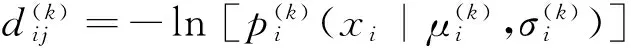
2.3参量优化

为了强化FCM算法的空间约束能力，以获取准确的分割结构，采用局部概率将其隶属度函数优化为

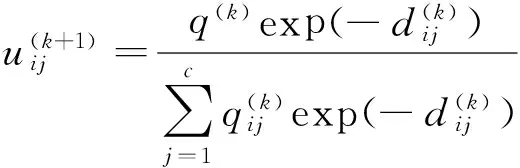
如此不仅考虑了分类的模糊性，还考虑到了图像信息的随机性。通过最大化来获取分割标记

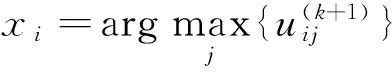
核空间的MRFFCM聚类算法还需要更新均值和标准偏差，即将其分别优化为

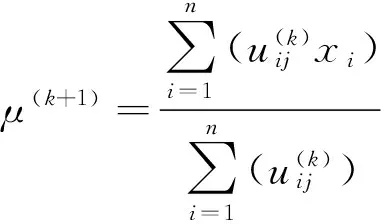
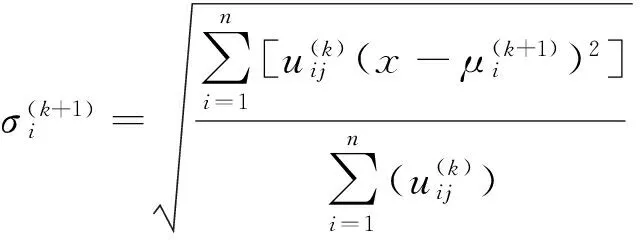
2.4算法步骤

算法的主要程序可描述如下。

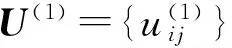
步骤2在第k个迭代中，利用空间范围建立能量矩阵

步骤3用高斯表达式计算MRF的局部先验概率，得到局部先验概率矩阵

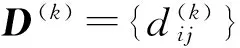
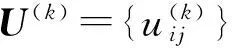
步骤6计算一个新的点，生成新矩阵

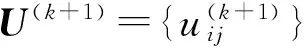
3　实验结果及分析

为验证改进算法的有效性，选取图像进行分割测试，并将其与FCM算法、KFCM算法和MRFFCM算法的抗噪和分割能力加以对比。在此给出9幅典型图像并加入椒盐噪声和高斯噪声后的分割对比结果，并以峰值信噪比(Peak Signal To Noise Ratio, PSNR)来衡量相关算法的抗噪性能。

3.1无噪声干扰图像分割测试

无噪声分割测试的实验结果如图1所示。

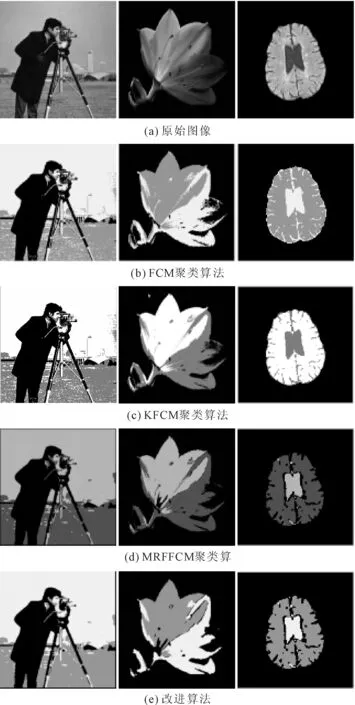
图1　无噪声干扰分割结果

由图1可见，在视觉效果上，改进算法的分割效果优于其他3种算法：FCM算法、KFCM算法分割效果较差；MRFFCM算法相比前两种算法分割结果有了明显的改善；改进算法获得分割结果目标轮廓最清晰完整。

3.2高斯噪声干扰图像分割测试

对如图2(a)所示的Lena图、几何图形和Varde图，添加均值为0，均方差分别为26、72和18的高斯噪声，如图2(b)所示,相关分割测试结果见图2。

图2　高斯噪声干扰分割结果

分割图像的峰值信噪比如表1所示，点分错误率表2所示。

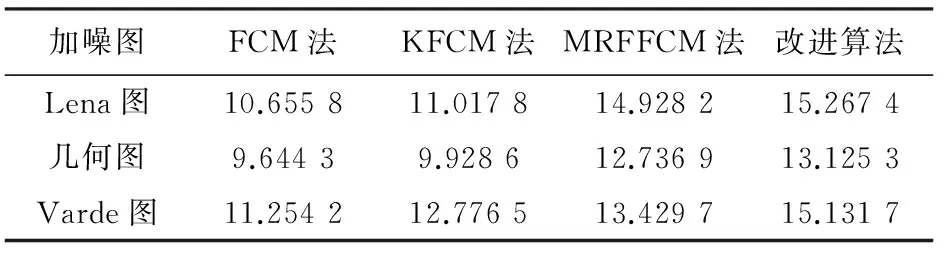
表1　抗高斯噪声的分割算法性能PSNR比较

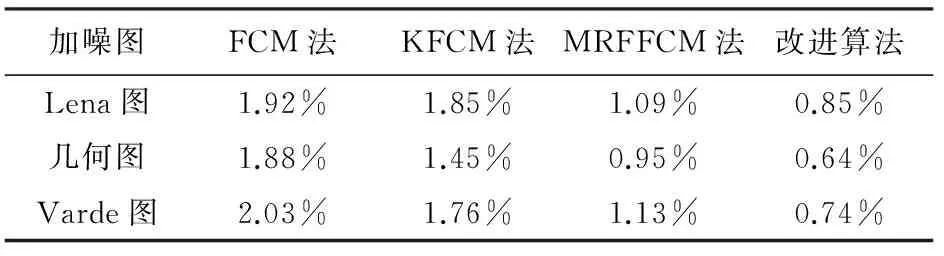
表2　抗高斯噪声的分割算法点分错误率

由图2及表1和表2可见，改进算法与另3种算法相对比，有较显著差异：FCM算法和KFCM算法的去噪和分割能力较差；MRFFCM算法去噪能力相对于前两种本文算法较好；改进算法将3种算法相结合，所得去噪和分割效果优于其他3种算法。

3.3椒盐噪声干扰图像分割测试

对如图3(a)所示的赫本图、花朵图和五星图，分别添加强度40%、30%和20%的椒盐噪声，如图3(b)所示，相关分割测试结果如图3所示。

图3　椒盐噪声干扰分割结果

分割图像的峰值信噪比如表3所示，点分错误率表4所示。

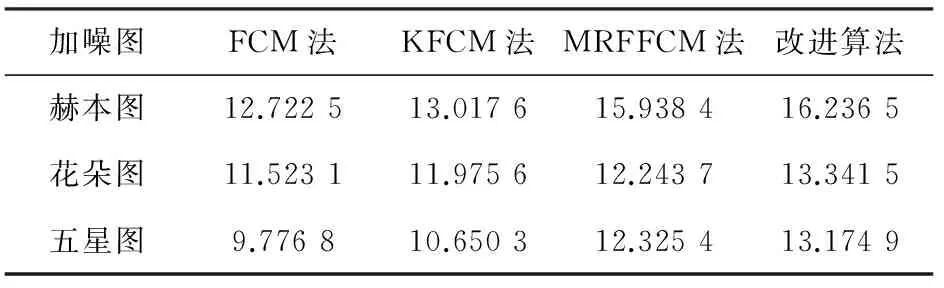
表3　抗椒盐噪声的分割算法性能PSNR比较

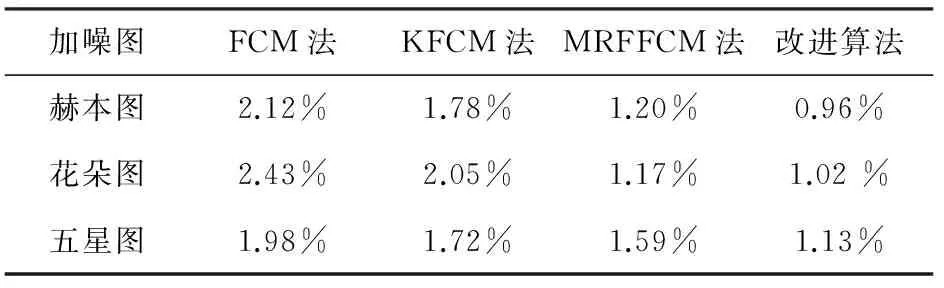
表4　抗椒盐噪声的分割算法点分错误率

由图3及表3和表4可见，在视觉效果上，改进算法的抗噪能力优于其他3种算法：FCM聚类算法、KFCM聚类算法分割效果较差；MRFFCM聚类算法相比前两种算法分割结果有了明显的改善；改进算法获得分割结果噪声较少且目标轮廓清晰完整。

4　结语

将核函数与MRFFCM算法相结合构造新的算法，通过对不同图像不添加噪声和添加椒盐、高斯噪声进行分割测试，结果表明基于核空间的马尔科夫随机场模糊聚类算法相比现有相关算法获得更好的抗噪性能。

[1]BORA D J, GUPTA A K. A Comparative Study Between Fuzzy Clustering Algorithm and Hard Clustering Algorithm[J/OL]. International Journal of Computer Trends and Technology, 2014,10(2):108-113[2016-01-14].http://dx.doi.org/10.14445/22312803/IJCTT-V10P119.

[2]KANDWAL R, KUMAR A, BHARGAVA S. Review: Existing Image Segmentation Techniques[J/OL]. International Journal of Advanced Research in Computer Science and Software Engineering,2014,4(4):153-156[2016-01-14].http://www.ijarcsse.com/docs/papers/Volume_4/4_April2014/V4I4-0130.pdf.

[3]SHIVHARE P, GUPTA V. Review of Image Segmentation Techniques Including Pre & Post Processing Operations[J/OL]. International Journal of Engineering and Advanced Technology, 2015, 4(3):153-157[2016-01-14].http://www.ijeat.org/attachments/File/v4i3/C3782024315.pdf.

[4]申铉京,何月.基于空间信息及隶属度约束的FCM图像分割算法[J/OL].北京工业大学学报,2012,38(7):1073-1078[2016-01-14].http://mall.cnki.net/magazi ne/article/BJGD201207023.htm.

[5]李琳,范九伦,赵凤.模糊C-均值聚类图像分割算法的一种改进[J/OL].西安邮电大学学报,2014,19(5):56-60[2016-01-14].http://dx.chinadoi.cn/10.13682/j.issn.2095-6533.2014.05.011.

[6]AHMED M N, YAMRNY S M, et al. A modified fuzzy C-means algorithm for bias field estimation and segmentation of MRI data[J/OL]. IEEE Transactions on Medical Imaging, 2002, 21(3):193-199[2016-01-14].http://ieeexplore.ieee.org/xpl/articleDetails.jsp?arnumber=996338.DOI:10.1109/42.996338.

[7]XIANG D L, TANG T, HU C B, et al. A kernel clustering algorithm with fuzzy factor: application to SAR image segmentation[J/OL]. IEEE Geoscience and Remote Sensing Letters,2014,11(7): 1290-1294[2016-01-14].http://ieeexplore.ieee.org/xpl/articleDetails.jsp?arnumber=6685860.DOI:10.11 09/LGRS.2013.2292820.

[8]GONG M, LIANG Y, SHI J, et al. Fuzzy C-Means Clustering with Local Information and Kernel Metric for Image Segmentation[J/OL].IEEE Transactions on Image Processing,2013,22(2): 573-584[2016-01-14].http://dx.doi.org/10.1109/TIP.2012.2219547.

[9]LIN K P.A Novel Evolutionary Kernel Intuitionistic Fuzzy C-means Clustering Algorthm[J/OL].IEEE Transaction on Fuzzy Systems,2014,22(5):1074-1087[2016-01-14].http://dx.doi.org/10.1109/TFUZZ.2013.2280141.

[10] 程可嘉.基于核函数的模糊聚类算法研究[D/OL].成都:电子科技大学,2009:8-23[2016-01-10].http://d.wanfangdata.com.cn/Thesis/Y1464174.

[11] CHATZIS S P, VARVARIGOU T A. A Fuzzy Clustering Approach Toward Hidden Markov Random Field Models for Enhanced Spatially Constrained Image Segmentation[J/OL].IEEE Transactions on Fuzzy Systems,2008,16(5):1351-1361[2016-01-14].http://dx.doi.org/10.1109/TFUZZ.2008.2 005008.

[12] 刘国英,王爱民.基于MRF 模型的鲁棒FCM分割算法[J/OL].计算机工程与科学,2012,34(10): 108-112[2016-01-14].http://dx.chinadoi.cn/10.3969/j.issn.1007-130X.2012.10.022.[13] GONG M G, SU L Z, JIA M,et al. Fuzzy Clustering with a Modi?ed MRF Energy Function for Change Detection in Synthetic Aperture Radar Images[J/OL]. perception understanding of minist,2014,22(1):98-109[2016-01-14].http://dx.doi.org/10.1109/TFUZZ.2013.2249072.

[14] 汪廷华,陈俊婷.核函数的选择研究综述[J/OL].计算机工程与设计,2012,33(3):1181-1186[2016-01-14].http://dx.chinadoi.cn/10.3969/j.issn.1000-7024.2012.03.068.

[责任编辑:瑞金]

Image fuzzy clustering based on kernel space Markov random field

QU Hanzhang1,XU Dan2,WU Chengmao3

(1.School of Science, Xi’an University of Posts and Telecommunications, Xi’an 710121, China;2.School of Communication and Information Engineeing, Xi’an University of Posts and Telecommunications, Xi’an 710121, China；3.School of Electronic Engineering, Xi’an University of Posts and Telecommunications, Xi’an 710121, China)

The kernel function is introduced to improve the Markov random field image fuzzy clustering algorithm, it is used to transform the input space information samples from the Markov random field into a high dimensional feature space, where the clustering is executed. The improved algorithm is implemented upon some standard images with Gaussian noise or salt and pepper noise for clustering, the visual effect and the peak signal to noise ratio of the segmented images shows that, the ability of clustering, classification accuracy and anti noise performance are all improved.

fuzzy C-means clustering, kernel function, Markov random field, spatial information

10.13682/j.issn.2095-6533.2016.05.003

2016-03-17

国家自然科学基金重点资助项目(61136002)；陕西省自然科学基金资助项目 (2014JM8331,2014JQ5183,2014JM8307)；陕西省教育厅科学研究计划资助项目(2015JK1654)

屈汉章 (1956-)，男，教授，从事小波理论及其应用研究。E-mail:qhz_002@163.com

徐丹(1991-)，女，硕士研究生，研究方向为通信与信息系统。E-mail:850578076 @qq.com

TP391.41

A

2095-6533(2016)05-0015-06