测试条件对环氧树脂损耗因子和玻璃化转变温度的影响

吕 珏, 冯捷敏

(1. 上海华谊(集团)公司技术中心， 上海 200241；2． 上海市力学在能源工程中的应用重点实验室， 上海 200072； 3. 上海大学理学院 力学系， 上海 200444)



测试条件对环氧树脂损耗因子和玻璃化转变温度的影响

吕 珏, 冯捷敏

(1. 上海华谊(集团)公司技术中心， 上海 200241；2． 上海市力学在能源工程中的应用重点实验室， 上海 200072； 3. 上海大学理学院 力学系， 上海 200444)

采用动态力学分析(DMA)研究环氧树脂，分析了扫描频率、加载模式和升温速率对环氧树脂损耗因子和玻璃化转变温度的影响。结果表明：扫描频率越大，所测得的玻璃化转变温度也越高，损耗因子峰值也越高，峰宽也越宽，玻璃化转变区域也越大；升温速率越快，玻璃化转变温度也越高，损耗因子峰值越低；利用Arrhenius 公式计算得到环氧树脂玻璃化转变所需要的活化能△E，在拉伸模式下的△E比弯曲模式下的大很多。

动态力学分析； 环氧树脂； 损耗因子； 扫描频率； 加载模式； 升温速率

0 前言

动态力学分析(DMA)是在周期交变负荷作用下研究材料的热力学性能的方法。它使高分子材料的力学性能与温度、作用的频率联系起来, 反映了在强迫振动下材料的储存模量E′、损耗模量E″及损耗因子tanδ随温度T的变化情况[1]。DMA是一种评价材料的耐热性、耐寒性、相容性、减震阻尼效率及加工工艺性能等的方法[2]。

损耗因子tanδ对于研究高分子材料的性能有着至关重要的作用。例如：从高分子材料的tanδ-T曲线，可以根据tanδ各个峰值的位置，得到材料各级玻璃化转变温度；其次,tanδ还可以表征高分子材料的阻尼性能。阻尼材料要求高内耗, 即要求tanδ大。理想的阻尼材料应在整个工作温度区间内都有较大的内耗, 即希望材料的tanδ-T曲线变化平缓, 与温度坐标之间的包络面积尽量大。利用材料的DMA温度谱,很容易选择出适合于特定温度范围内使用的阻尼材料[3]。损耗因子还可以评价高分子材料的延展性和断裂韧性[4-6]，它们都与损耗因子的β转变的宽度、温度有关。

在DMA测试过程中，频率、振幅、升温速率、加载模式等都会影响高分子材料的动态力学性能。研究结果表明:随着扫描频率增加，高分子材料的玻璃化转变温度上升[7]。狄海燕 等[8]研究了振幅对动态力学性能的影响。周芳 等[9]研究了升温速率对DMA测试结果的影响，但是目前很少研究频率、升温速率和加载模式对损耗因子的影响，因此，笔者选用环氧树脂为研究对象，研究频率、升温速率和加载模式对损耗因子和玻璃化转变温度的影响，以及在不同加载模式下环氧树脂玻璃化转变所需活化能的变化规律。

1 实验

1.1 材料

实验选用纯环氧树脂，由上海玻璃钢研究院提供。实验选用四种不同加载模式，各种加载模式下的试样尺寸,如表1所示。

1.2 仪器及方法

采用TA公司的DMA Q 800动态力学分析仪;选用DMA中多频-温度-应变模式对材料进行温度扫描。测试条件：振幅为20 μm，频率分别为1、5、10、40、100和160 Hz。升温速率分别为1、3、10和15 K/min。测试温度范围从室温到393 K。选用三点弯和拉伸加载模式时，预先施加0.5 N的预紧力以保证测试样品始终被夹紧；在使用单悬臂和双悬臂加载模式时不需要施加预紧力。

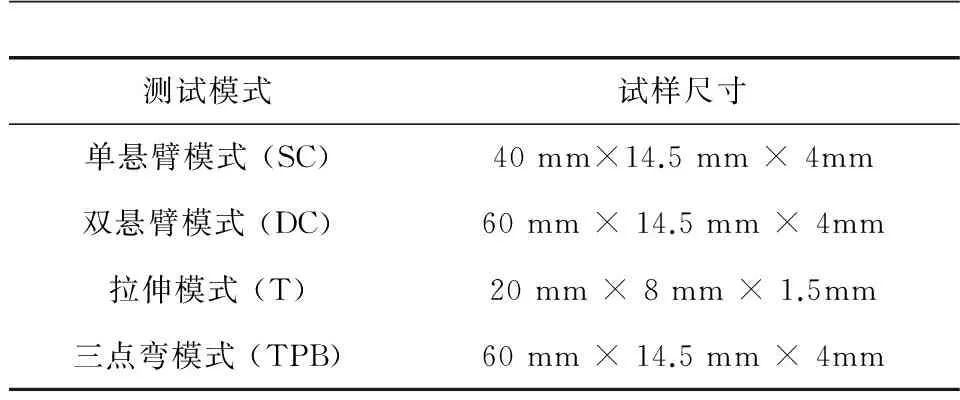
表1 四种加载模式下的试样尺寸

2 结果与讨论

2.1 频率对损耗因子和玻璃化转变温度的影响

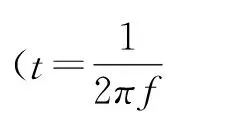
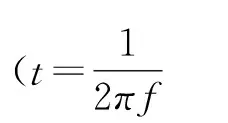
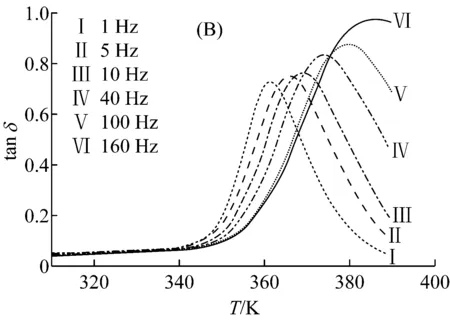
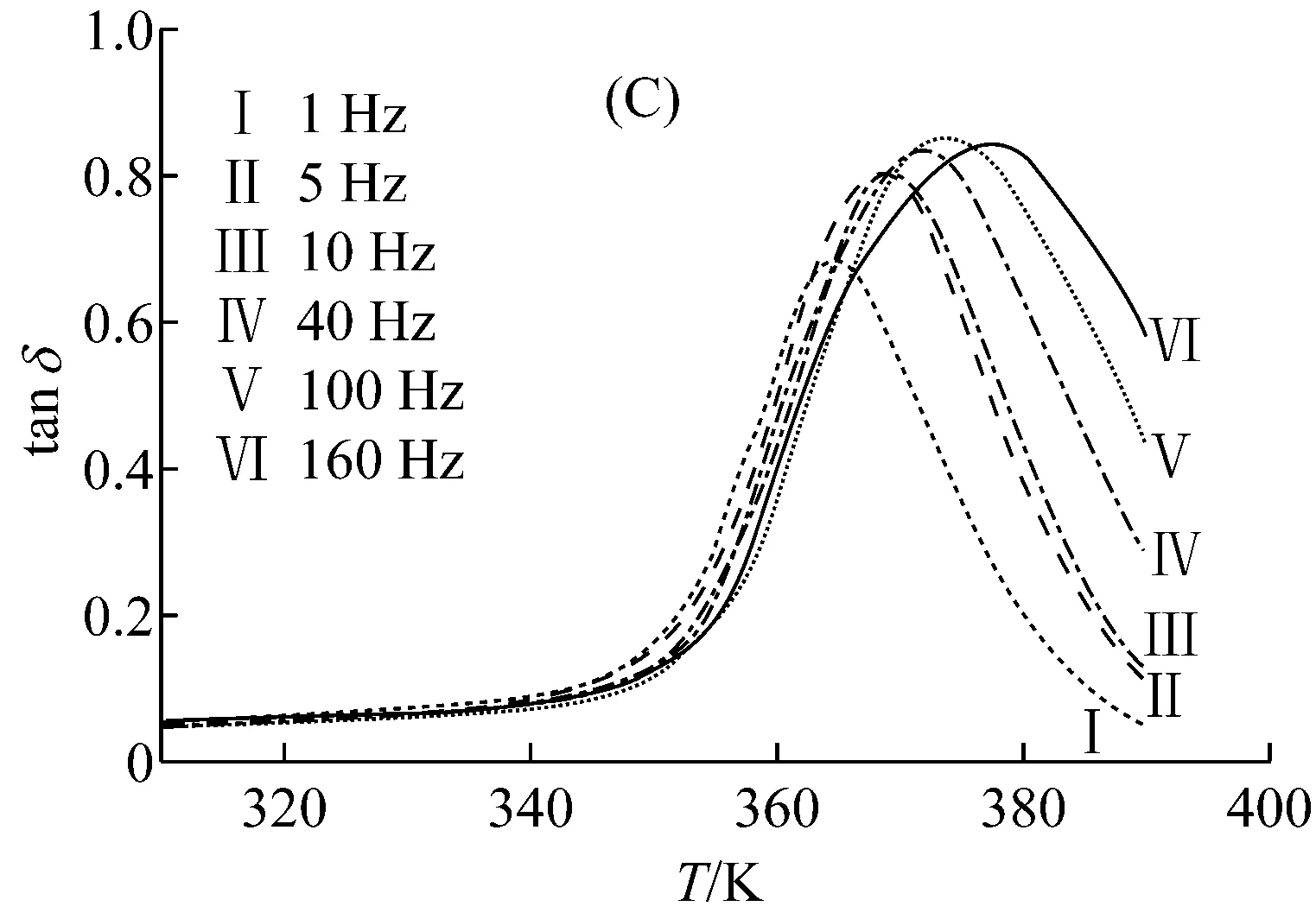
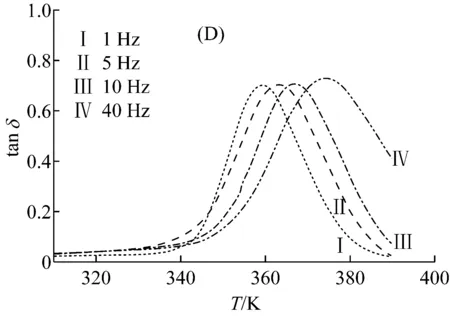
(A) 单悬臂模式， (B) 双悬臂模式， (C) 拉伸模式， (D) 三点弯模式 (升温速率S=3 K/min)

2.2 升温速率对损耗因子和玻璃化转变温度的影响

图2为固定扫描频率f=1Hz，双悬臂载荷模式下，升温速率对环氧树脂的Tg影响。由图2可知：随着升温速率的增加，所测量得到的Tg升高。这是由于非晶聚合物的玻璃化转变不是热力学相态转变过程，而是与实验室时间标尺有关的松弛行为，所以在测定非晶聚合物的玻璃化转变温度时，温度改变速率(升温或降温速率)对该过程进行的路径和结果都会产生显著影响。升温速率对测量的影响可能有两方面原因：一方面，由时间-温度等效原理可知：提高升温速率相当于缩短观测时间，只有温度更高，聚合物的松弛时间才能降低到和观测时间相同，聚合物才进入玻璃化转变；另一方面，升温速率提高，试样表里温差就可能增大，导致试样内部还没有进入玻璃化转变，但是由于升温速率较快，实验显示温度已经超过了其玻璃化转变温度。

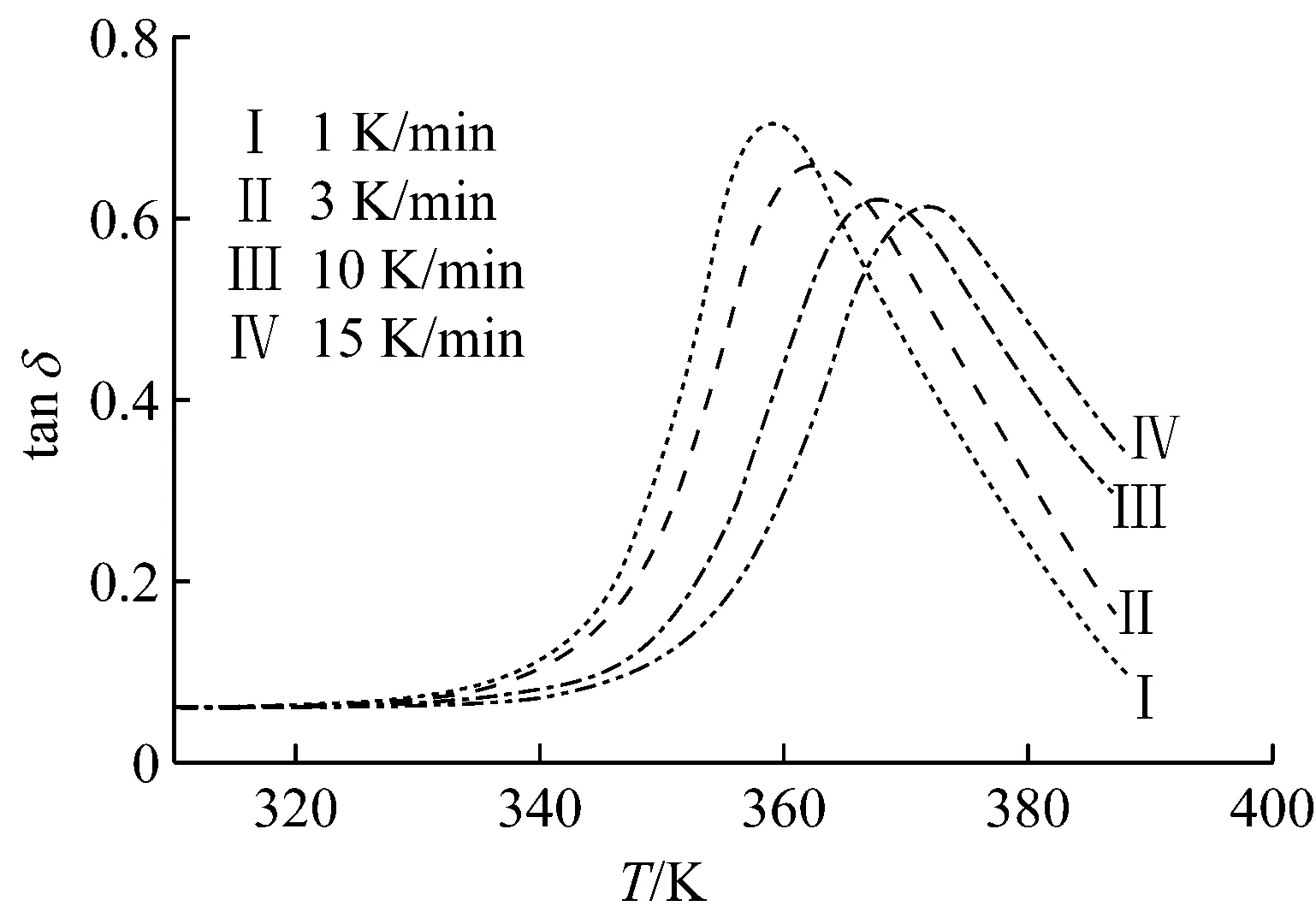
图2 双悬臂模式下升温速率对环氧树脂损耗

从图2还可以看出：损耗因子的峰值随着升温速率加快而降低。这可能是，因为升温速率加快，导致试样外部和内部温差可能增大，当内部达到玻璃化转变温度时，外部已经进入了橡胶态，或者说外部达到玻璃化转变温度时，内部还处于玻璃态。由于橡胶态或者玻璃态的内耗均小于玻璃化转变区时的内耗，所以内部和外部内耗叠加就变小了。

2.3 不同加载模式下活化能

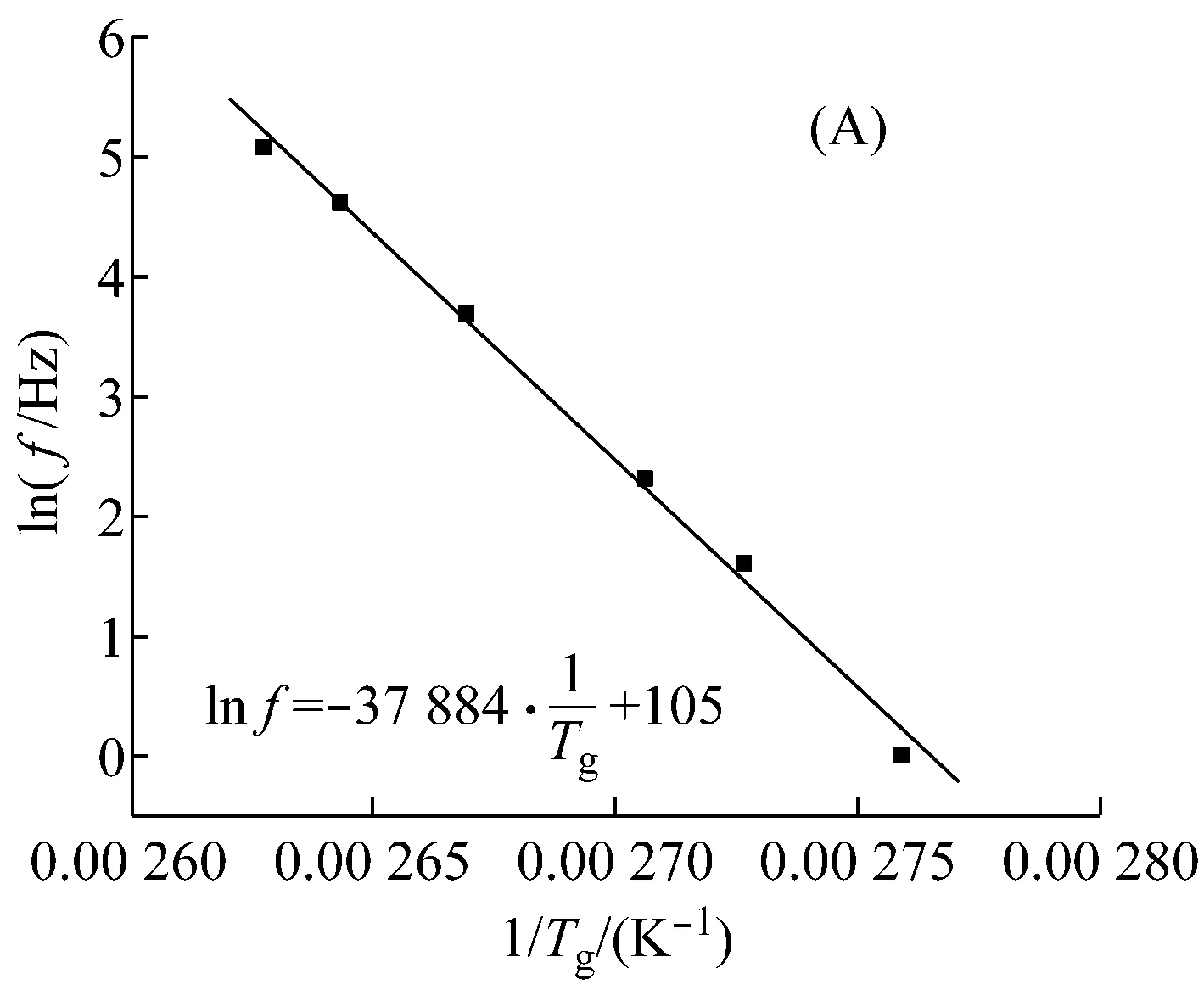
文献[13]指出：当f提高10倍时，Tg的变化可用式(1)表示。

(1)

式中:Tg1和Tg2分别为f和10f时的玻璃化转变温度;R为气体常数,8.314 J/mol·K，△E为活化能，J/mol,与高分子链段运动密切相关。有不少学者[14-16]应用Arrhenius公式描述如下：

lnf=lnA-ΔE/RTg

(2)

式中:A为常数。

图3为环氧树脂在不同载荷模式下lnf与1/Tg的关系曲线。表2列出了四种载荷测试模式下环氧树脂的玻璃化转变活化能。

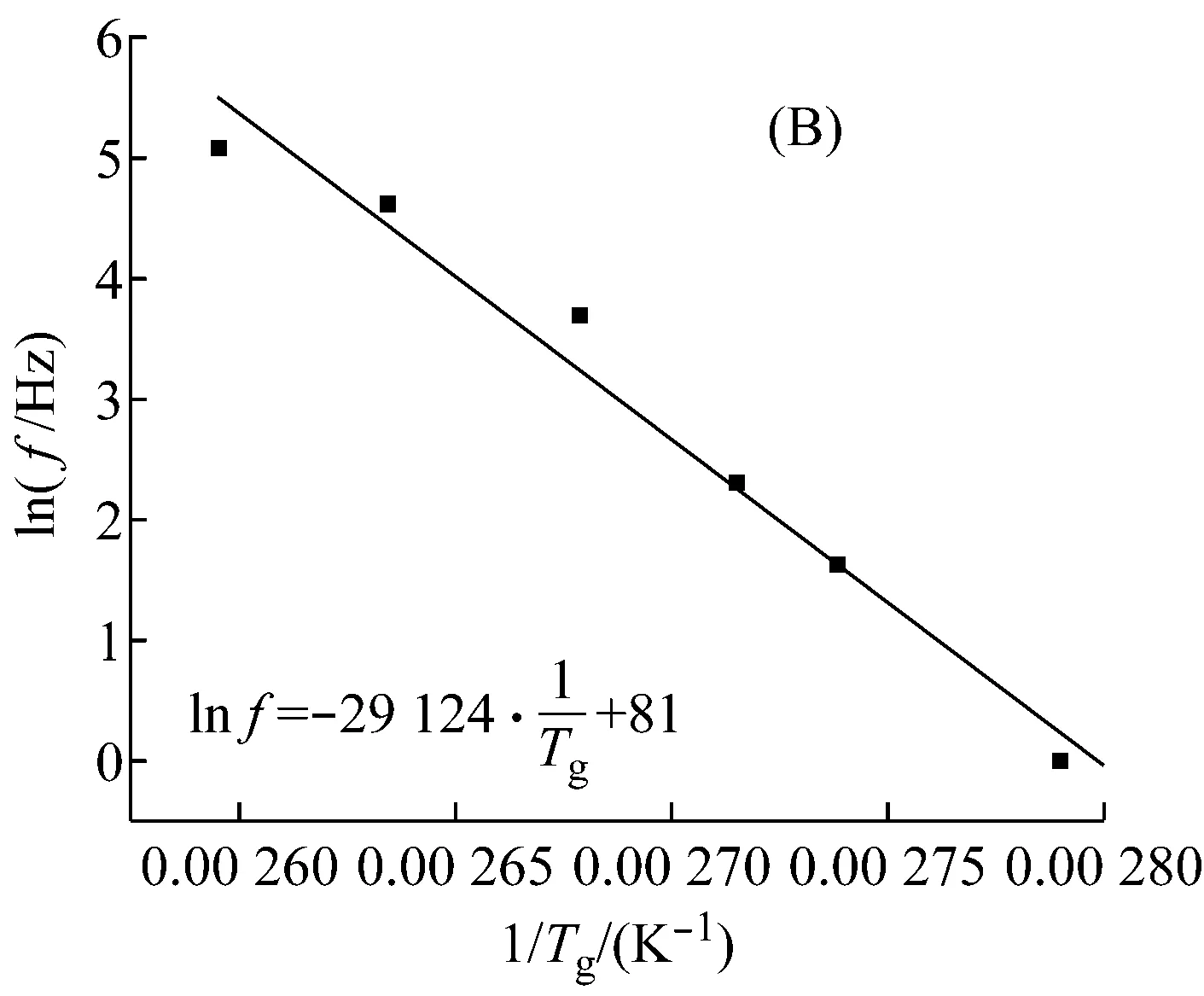
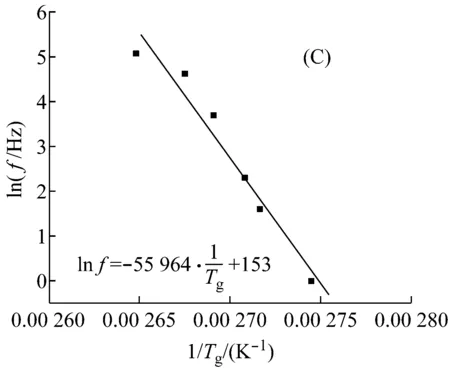
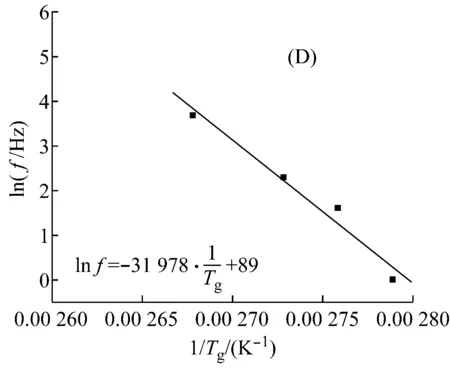
(A) 单悬臂模式， (B) 双悬臂模式， (C) 拉伸模式， (D) 三点弯模式

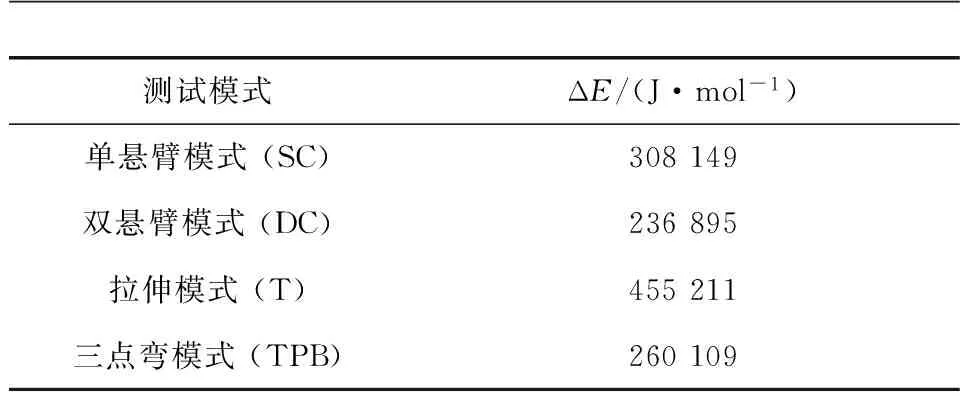
测试模式ΔE/(J·mol-1)单悬臂模式(SC)308149双悬臂模式(DC)236895拉伸模式(T)455211三点弯模式(TPB)260109

由表2可见:拉伸模式下测得的△E比其他三种弯曲模式下的△E要大许多；其他三种弯曲模式下的△E相差不多。这说明环氧树脂在拉伸模式下发生玻璃化转变所需要的能量比弯曲模式下所需要的能量大得多。这个现象与外力场对聚合物构象变化影响有关。非晶态聚合物通常可视为可任意卷曲的无规则线团结构，在玻璃化转变过程中，分子链键的内旋转运动必然受到邻近链段牵制,在外力场作用下，分子链段沿外力方向运动，并导致构象数目的变化，显然沿应力方向上构象数目占优[14,17]。此外，应力对分子链σ键的内旋转运动起到诱导作用，改变了构象转变的时间。根据管道模型，分子链段运动并非沿某一直线方向，其运动轨迹为一条“弓背形”管道，犹如一条蛇在稠密树干的阻扰下缓慢地爬行,所以在梯度应力作用下更有利于诱导分子链的内旋运动,导致了在弯曲模式下的玻璃化转变所需的△E小于拉伸模式下的△E。

柳洪超 等[11]指出:玻璃化转变温度不只与测试频率符合Arrhenius公式;用差示扫描量热仪所测得的玻璃化转变温度与其升温速率也符合Arrhenius公式：

lnS=lnB-ΔE/RTg

(3)

式中:B为常数，S为升温速率,K/min。

笔者将这种关系引入到DMA中，即DMA所测得的Tg与其升温速率也满足式(3)。

图4为环氧树脂在双悬臂模式下lnS与1/Tg的关系曲线。由其斜率可以计算得到环氧树脂在双悬臂模式下△E=23 178 J/mol。与表2中双悬臂模式下测得的数据比较,可以发现:由不同升温速率测得的与由不同频率测得的ΔE没有明显差别。

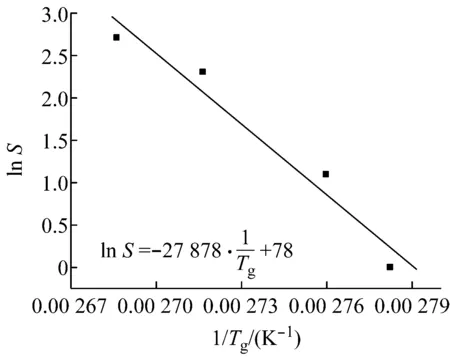
图4 环氧树脂ln S与1/Tg的关系曲线(f=1 Hz)

3 结语

以环氧树脂为研究对象，研究了扫描频率、升温速率和加载模式对环氧树脂损耗因子和玻璃化转变温度的影响；计算了环氧树脂在不同载荷模式下玻璃化转变所需的活化能。

(1) 测试的扫描频率越大，测量得到的Tg升高，损耗因子峰值也越高，损耗峰宽也越宽，玻璃化转变区域也越大。

(2) 在DMA测试中,升温速率越快，测量得到的Tg升高，损耗因子峰值越低。

(3) 环氧树脂在拉伸模式下测试玻璃化转变所需的活化能比在其他三种弯曲模式下的大很多。

[1] 高家武.高分子材料近代测试技术[M]. 北京：北京航空航天大学出版社, 1994.

[2] 欧国容, 张德霖. 高分子科学与工程实验[M]. 上海：华东理工大学出版社, 1991: 57-77.

[3] 王雁冰, 黄志雄, 张联.DMA在高分子材料研究中的应用[J].国外建材科技,2004, 25(2): 25-27.

[4] DAVID L,ETIENNE S.Molecular mobility in para-substituted polyaryls(1). Sub-Tg relaxation phenomena in poly (aryl ether ether ketone)[J]. Macromolecules, 1992, 25 (17): 4302-4308.

[5] HEIJBOER J.Dynamic mechanical properties and impact strength [J]. Journal of Polymer Science (Part C), 1968, 16: 3755-3763.

[6] BOYER RF. Mechanical motions in amorphous and semi-crystalline polymers [J]. Polymer, 1976, 17 (2): 996-100.

[7] 魏莉萍, 刘运传, 郑会保, 等.DMA测量高聚物黏弹性参数重复性研究[J]. 工程塑料应用,2007,35(6):54-57.

[8] 狄海燕, 吴世臻, 杨中兴, 等.各种因素对动态热机械分析结果的影响[J]. 高分子材料科学与工程, 2007,23(4):188-191.

[9] 周芳, 蓝桂美, 胡居花,等. 环氧模塑料玻璃化温度的测定方法及其影响因素[J].电子工业专用设备, 2009(7):1-6.

[10] 宋华杰，董海山，郝莹, 等. TATB基高聚物黏结炸药及其粘结剂的玻璃化温度与DMA测量频率关系的研究[J]. 含能材料,2001, 9(1): 10-13.

[11] 柳洪超, 吴立军, 尤瑜升,等.用玻璃化转变评价氟橡胶的低温性[J]. 应用化工, 2007, 36(10): 1007-1010.

[12] 过梅丽. 高聚物与复合材料的动态力学热分析[M]. 北京: 化学工业出版社, 2002.

[13] NIELSEN L E.Mechanical properties of polymers [M]. New York: Van Nostrand Reinhold, 1962.

[14] 符若文. 高分子物理[M]. 北京: 化学工业出版社, 2005.

[15] 过梅丽. 世界先进的动态机械热分析仪(DMTA)及其应用[J]. 现代科学仪器,1996(1): 55-58.

[16] BARTON J M, GREENFIELD D C L.The use of dynamic mechanical methods to study the effect of absorbed water on temperature-dependent properties of an epoxy resin-carbon fibre composite [J]. British Polymer Journal, 1986, 18(1): 51-56.

[17] SZABO J P, KEOUGH I A. Method for analysis of dynamic mechanical thermal analysis data using the havriliak negami model [J]. Thermochimica Acta, 2002,392(18): 1-12.

Influence of Testing Conditions on Loss Factor and Glass Transition Temperature of Epoxy

LV Jue1, FENG Jie-min2,3

(1．Technology Research Institute of Shanghai Huayi Group，Shanghai 200241， China；2.Shanghai Key Laboratory of Mechanics in Energy Engineering,Shanghai 200072, China; 3.Department of Mechanics, College of Science, Shanghai University, Shanghai 200444, China)

Epoxy resin was studied by using dynamical mechanics analysis (DMA). The influences of the loading frequency, loading mode and heating rate on the loss factor and glass transition temperature of epoxy were analyzed. The results show that the higher loading frequency is chosen, the higher glass transition temperature is obtained, the peak of loss factor becomes higher and wider, and the region of the glass transition appears wider. The faster heating rate is chosen, the higher glass transition temperature is obtained, and the lower peak of loss factor is got.The activation energies, △E, of glass transition in the different loading modes are calculated by Arrhenius equation. The activation energy in the tensile loading mode is much larger than the one in the bending loading mode.

dynamical mechanics analysis; epoxy; loss factor; loading frequency; loading mode; heating rate

吕 珏(1980—)，女，本科生，从事材料物性分析的研究

TQ 320

A

1009-5993(2016)02-0025-05

2016-01-11)