可调行距插秧机秧箱调节机构丝杠疲劳寿命预测

朱德泉，姚亚芳，武立权，蒋　锐，熊　玮

(1.安徽农业大学 工学院，安徽 合肥 230036； 2.安徽农业大学 农学院，安徽 合肥 230036)



可调行距插秧机秧箱调节机构丝杠疲劳寿命预测

朱德泉1，姚亚芳1，武立权2，蒋锐1，熊玮1

(1.安徽农业大学 工学院，安徽 合肥 230036； 2.安徽农业大学 农学院，安徽 合肥 230036)

为预测可调行距高速水稻插秧机秧箱调节机构梯形丝杠的使用寿命，应用相关疲劳理论和方法，推导梯形丝杠螺纹牙的疲劳寿命计算公式。利用Adams软件和Ansys软件建立调节机构的刚柔耦合模型并仿真，得到梯形丝杠最大轴向载荷为53.8 N，并在Ansys软件中建立螺纹牙的有限元模型，通过静力学分析得出最大范·米塞斯应力为188 MPa，小于材料的屈服极限。以静力学分析结果为初始条件，利用Ansys/fe-safe软件进行螺纹牙疲劳分析，得出梯形丝杠工作寿命为3 598 h，满足插秧机工作性能要求。

可调行距插秧机；秧箱；梯形丝杠；螺纹牙；疲劳寿命

我国经纬度跨度大，不同地区的水稻生长环境不同，稻作类型差异较大，对插秧行距要求也不一样，现有插秧机无法灵活调节插秧行距，难以满足不同地区水稻生产要求。目前，我国在可调行距插秧机方面的研究较少，扬州大学设计一种步行式行距可调插秧机，行距调节过程复杂[1-4]，难以推广。

秧箱是可调行距高速水稻插秧机的主要工作部件，由秧箱单元、调节机构、加强梁和导轨等组成。调节机构是秧箱核心机构。插秧机插秧时，秧箱调节机构随秧箱左右往复运动，受到交变载荷作用，易使其核心部件梯形丝杠螺纹表面产生疲劳裂纹，从而影响调节机构的工作可靠性、稳定性及寿命。因此，应用相关疲劳理论和方法，推导梯形丝杠螺纹牙的疲劳寿命计算公式，并利用Adams和Ansys软件建立秧箱刚柔耦合模型并仿真，预测梯形丝杠失效部位及疲劳寿命，以便提高维修保障的针对性。

1　总体结构和工作原理

秧箱由调节机构、加强梁、导轨和秧箱单元组成，其中，调节机构主要由梯形丝杠、螺母等组成，丝杠两端螺纹螺距相等、螺旋方向相反，如图1所示。插秧机调节插秧行距时需调节秧箱单元间距，与栽植臂位置匹配。插秧机工作前，转动丝杠，螺母做直线运动，并带动与之固定的左、右秧箱单元同时向中间或两侧移动，调节到所需行距位置。插秧机工作时，利用螺纹副自锁作用防止丝杠与螺母发生相对转动，保证横向送秧时秧爪取秧可靠性。

调节秧箱单元时，梯形丝杠受到轴向拉(压)力和摩擦转矩，由于螺旋副之间有较大滑动摩擦，因此，磨损是其主要失效原因[5]。根据耐磨性确定梯形丝杠和螺母的主要参数，如表1所示。

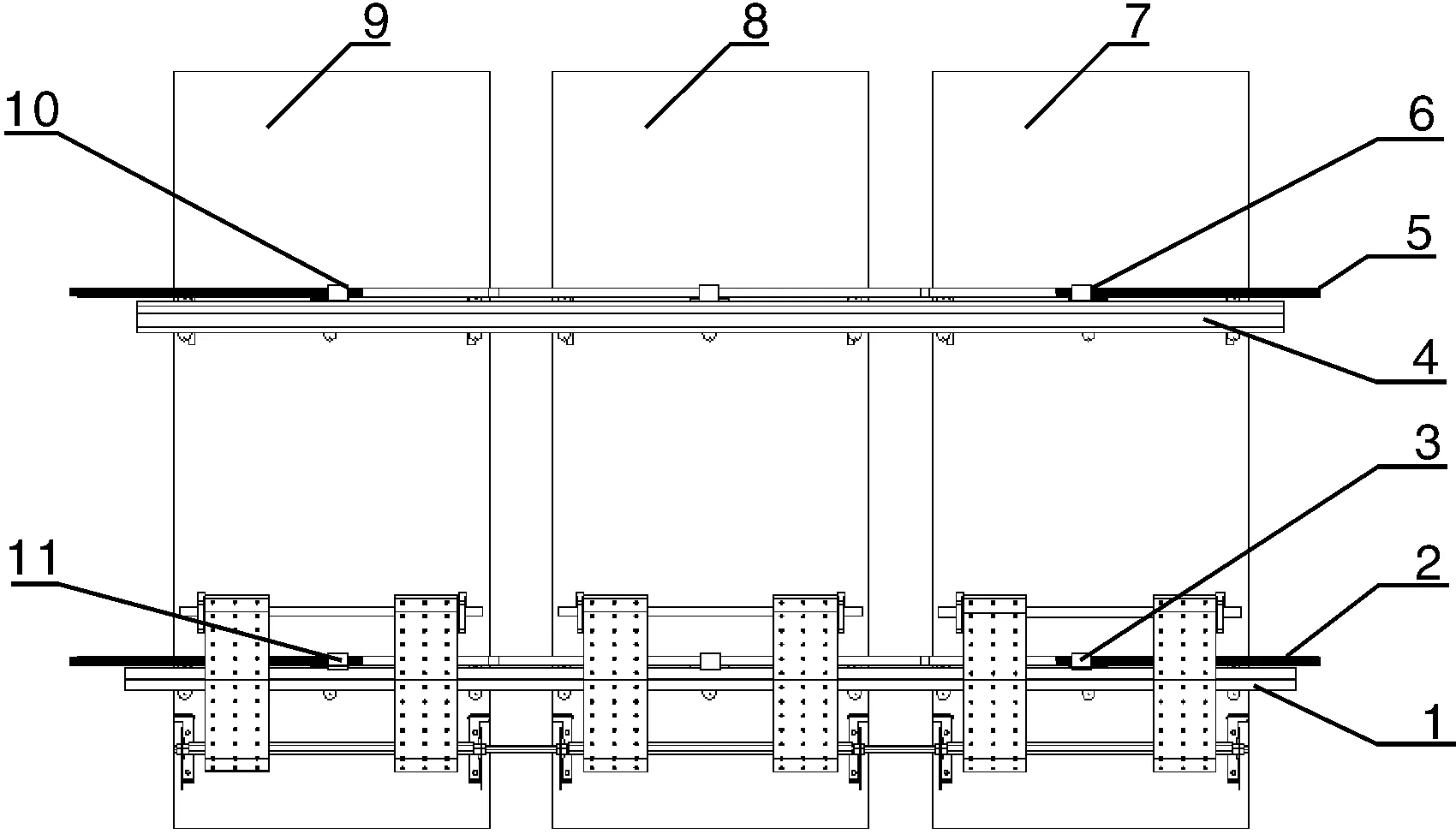
1.加强梁；2.下丝杠；3，6，10，11. 螺母；4.上导轨；5.上丝杠；7.右秧箱单元；8.中间秧箱单元；9.左秧箱单元。图1　可调行距插秧机秧箱结构示意图Fig.1　Structural schematic of seedling box of adjustable spacing transplanter

表1螺旋副的主要参数

Table 1Main parameters of screw pair

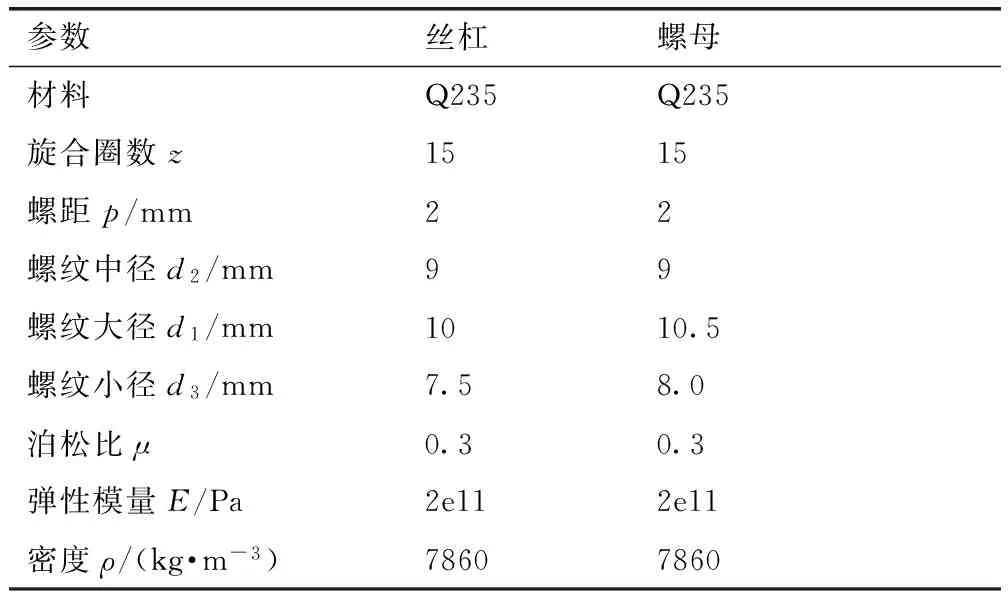
参数丝杠螺母材料Q235Q235旋合圈数z1515螺距p/mm22螺纹中径d2/mm99螺纹大径d1/mm1010.5螺纹小径d3/mm7.58.0泊松比μ0.30.3弹性模量E/Pa2e112e11密度ρ/(kg·m-3)78607860

2　疲劳寿命预测理论模型

疲劳破坏一般分为裂纹萌生、裂纹扩展和失稳扩展断裂3个发展阶段，失稳扩展断裂阶段时间很短，对疲劳寿命的影响可以不计[6-8]。根据经验，计算裂纹起始寿命时，常选择应变疲劳分析方法[9-10]。计算裂纹扩展寿命时，常选择断裂力学方法[11]。

2.1疲劳裂纹萌生寿命

疲劳裂纹起始寿命的定义与疲劳裂纹初始尺寸的定义相关。目前工程应用中，一般将形成长度或深度为0.25 mm的疲劳裂纹所经历的应力或应变循环次数，定义为疲劳裂纹的起始寿命Ni[12]，其计算表达式如下：

(1)

式(1)中：n—应变硬化指数；Ci—疲劳裂纹起始抗力系数；Δσeqv—当量应力幅；(Δσeqv)th—用当量应力幅表示的疲劳裂纹起始门槛值。

Ci和(Δσeqv)th均为材料常数，可用下式表示：

(2)

(3)

式(2)、(3)中：σf—材料的断裂强度或断裂真应力；εf—断裂延性；Δεc—理论应变疲劳极限值。

通常，拉伸试验只测定金属材料的抗拉强度σb，屈服强度σs(或σ0.2)、延伸率δ和断面收缩率ψ四个指标，弹性模量E可在手册中查到。式(2)、式(3)中的参数可由式(4)～式(8)求得。

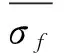
(4)

进而利用修正关系式：

(5)

当0.15≤εf≤3.0时，式(5)有效；当εf<0.15时，可不作修正。断裂延性εf可按下式求得：

εf=-ln(1-ψ)

(6)

应变硬化指数n的估算式为：

(7)

按式(7)估算的n误差为-0.03～0.30。

理论应变疲劳极限值的估算式为：

(8)

2.2疲劳裂纹扩展寿命

目前常见的疲劳裂纹扩展速率表达式是Paris和Ergogan率先提出的，通常简称为Paris公式：

da/dN=CΔKm

(9)

式(9)中，C，m分别由试验确定的系数和指数。

应力强度因子范围ΔK的计算式为：

(10)

式(10)中，Y为取决于裂纹长度a和试样宽度W的比值的几何因子。

将式(10)带入式(9)得

(11)

将变量分离得：

(12)

对式(12)两边同时积分可得

(13)

式(13)中：Np为疲劳裂纹扩展寿命；ac为临界裂纹长度。

2.3梯形丝杠螺纹牙疲劳寿命计算公式

参考紧固件螺纹要求，裂纹长度或条痕深度极限：

Lmax=0.015d+0.1

(14)

将d为10 mm带入式(14)得，梯形丝杠螺纹牙裂纹长度极限Lmax为0.25 mm，此值等于一般定义的起始裂纹长度。因此，可用螺纹牙疲劳裂纹起始寿命近似代替其全寿命。根据式(4)～式(8)计算得到Q235的拉伸性能，其中σs为235 MPa，σb为455 MPa，Ψ为54%，σf为595 MPa，n为0.28，E为196 GPa。

将Q235的拉伸性能参数带入式(2)和式(3)得，Ci为6.8×1011，(Δσeqv)th为127.8。将Ci和(Δσeqv)th带入式(1)，得到梯形丝杠螺纹牙疲劳裂纹起始寿命表达式：

(15)

由上述计算可知，利用试验分析法进行疲劳分析和寿命预测时，一般使用前人总结的经验公式来估计产品的寿命，许多相关参数与失效的定量关系不能在试验中得出，试验结论大多会受到不确定因素的影响。本文在刚柔耦合仿真分析和静力学分析的基础上，利用Ansys/fe-safe软件进行疲劳计算，可以大大避免设计的盲目性，实现产品的寿命周期设计等。

3　刚柔耦合仿真分析

3.1刚柔耦合模型建立

在秧箱刚柔耦合分析中，将梯形丝杠作为柔性体，其余部件均视作刚性件。先在Adams软件中建立秧箱的多刚体模型，再利用Ansys软件建立梯形丝杠的模态中性文件(*.mnf)，并将其导入Adams软件中进行刚柔替换处理，得到秧箱的刚柔耦合模型[13-15]，如图2所示。根据实际情况和简化原则，确定各构件之间的运动约束及系统载荷、驱动。

图2　秧箱刚柔耦合模型Fig.2　Coupled rigid and flexible model of seedling box

3.2动力学仿真结果

在Adams软件中对建立的秧箱刚柔耦合模型进行仿真计算，结果如图3所示，图3中负号表示与所选正方向相反。

由图3可知，秧箱每一行程的位移大小为165 mm，这与实际情况相符。秧箱启动瞬间，加速度较大，很短的时间内速度达到1.13 m·s-1；之后加速度降为0，秧箱保持1.13 m·s-1的速度平稳运行一段时间；秧箱换向时，加速度又瞬间增大，使速度在短时间内改变方向，并使其继续增大到1.13 m·s-1；之后加速度又降为0，速度保持在1.13 m·s-1；如此反复。上述仿真结果与秧箱运行实际情况基本相符，验证了刚柔耦合模型的正确性。

秧箱送秧时，丝杠与螺母旋合处丝杠的受力曲线，即丝杠受到的轴向载荷曲线，如图4所示，图4中负号表示与所选正方向相反。秧箱由静止到运动的瞬间，丝杠受到较大的轴向载荷F；之后由于秧箱匀速运动，F降为0；秧箱转向瞬间，F瞬间增大；换向以后F又降为0；如此反复。F最大值达53.8 N。

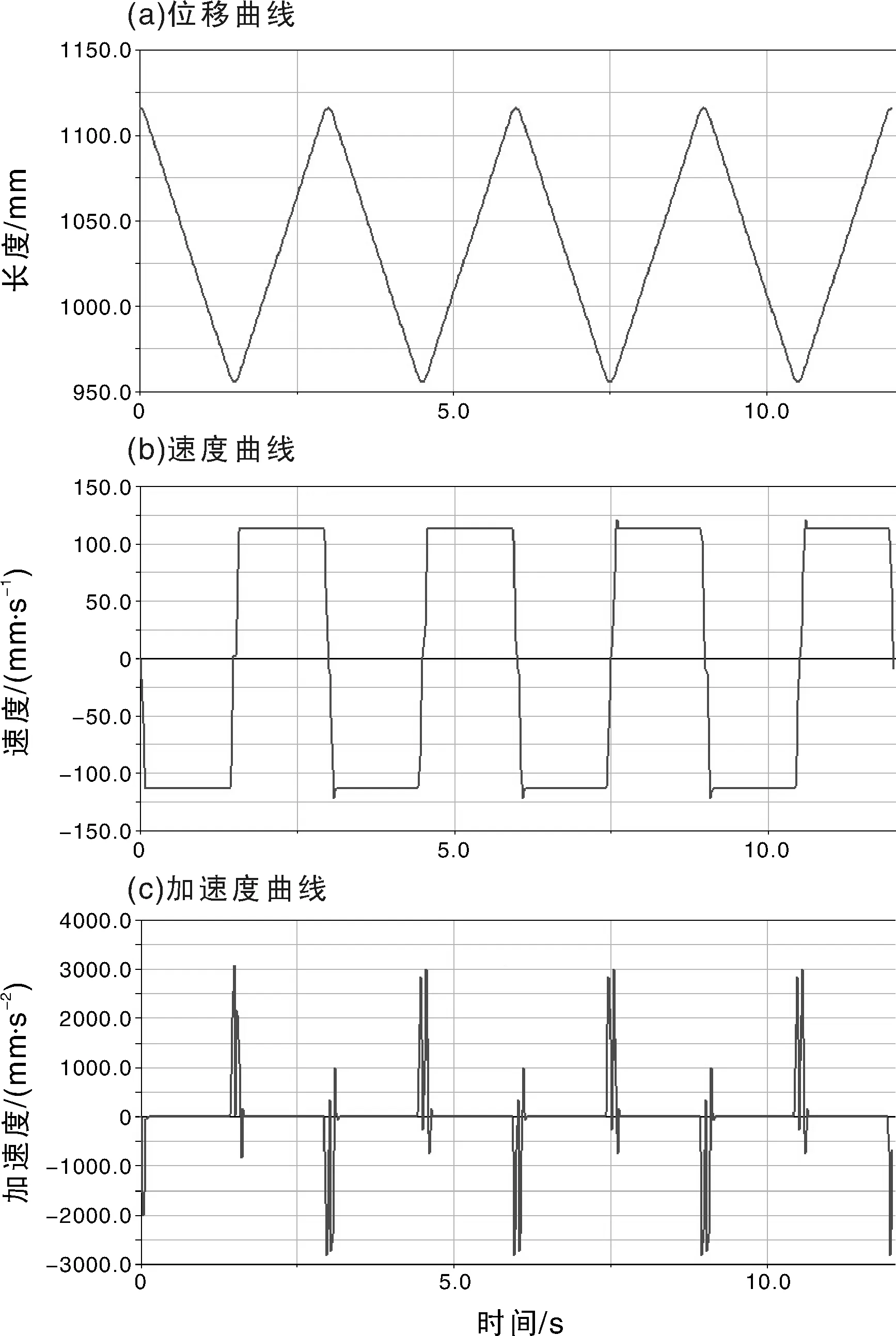
图3　秧箱运动学曲线Fig.3　Kinematics curve of seedling box

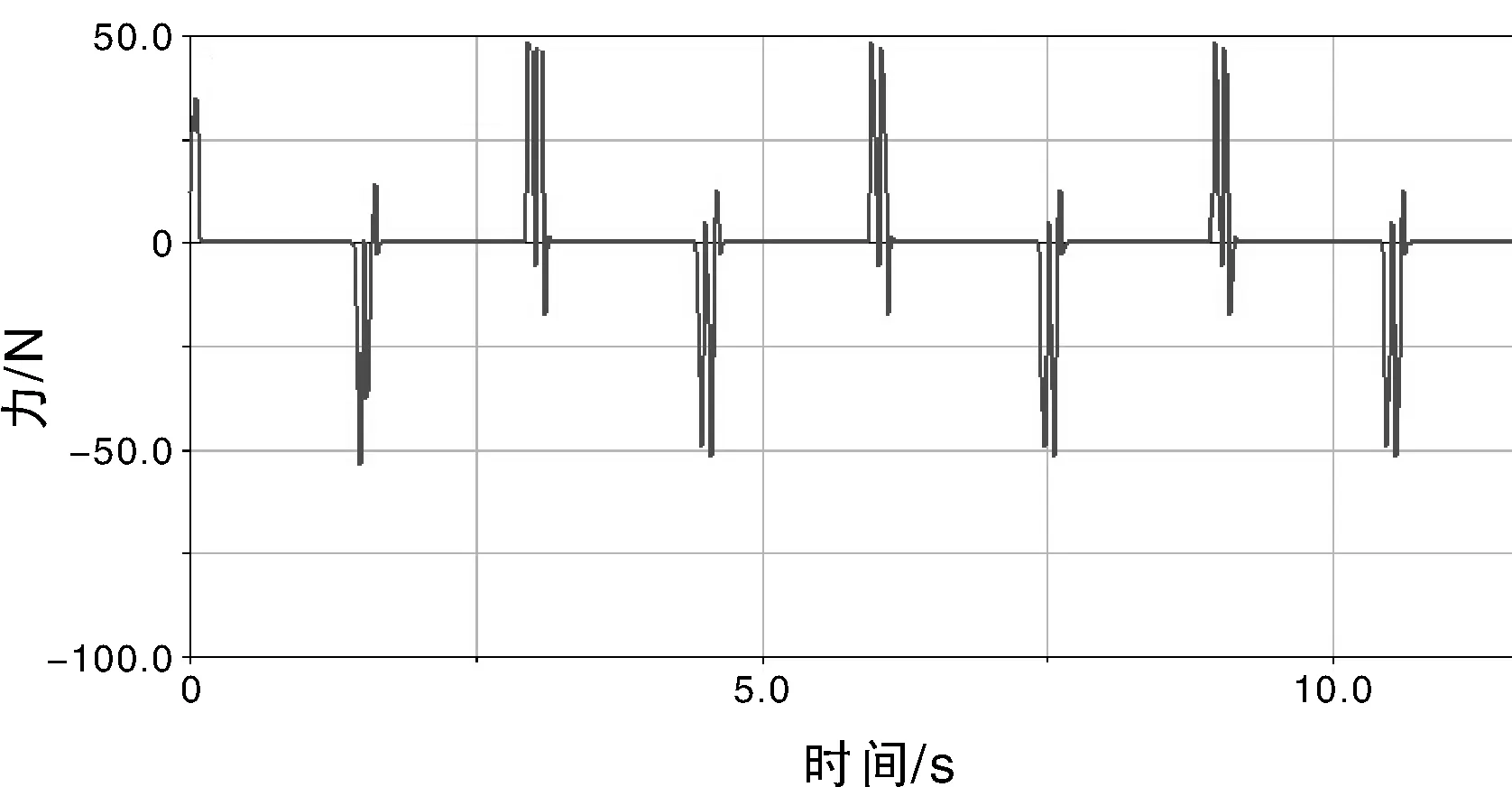
图4　丝杠轴向载荷曲线Fig.4　Curve of axial load of screw

4　螺纹牙疲劳分析

4.1螺纹牙静力学分析

4.1.1螺纹牙力学模型

丝杠受轴向载荷F，丝杠和螺母旋合圈数为z，假设各圈螺纹受力相等，则每圈螺纹承担的载荷F1为F/z。将丝杠一圈螺纹展开，传统计算假设F/z作用于中径圆周上[16]，如图5所示。

实际工作时，螺纹牙受到的力在一个平面上，如图6所示。插秧机工作时，随着秧箱换向，螺纹牙左右两面交替受到大小基本相等的压应力。

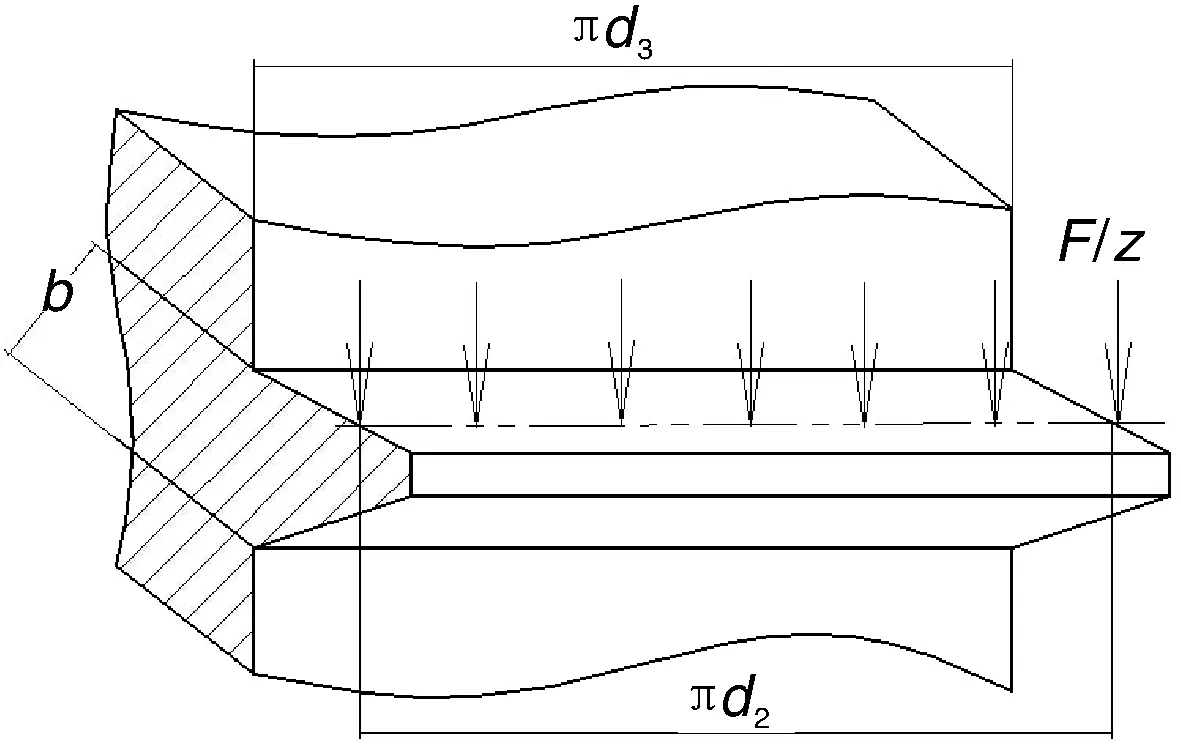
图5　螺纹牙传统受力分析Fig.5　Traditional force analysis of thread

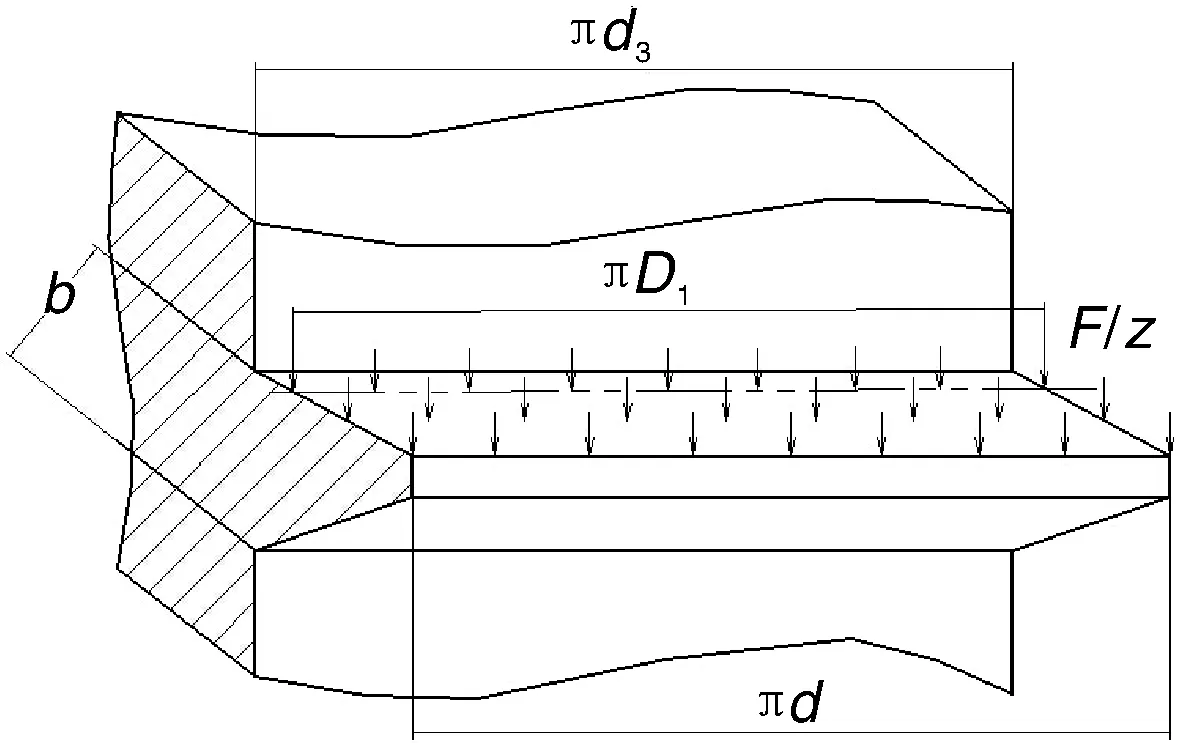
图6　螺纹牙实际受力分析Fig.6　Actual force analysis of thread

4.1.2螺纹牙有限元模型

利用Ansys软件建立梯形螺纹牙三维实体有限元模型，单元属性为Solid45[13]。网格生成后的模型如图7所示。

4.1.3螺纹牙静力学分析

根据刚柔耦合仿真分析结果，考虑螺纹牙因疲劳失效而承受的极限情况，取丝杠受到的轴向载荷为最大值，即F=53.8 N。插秧机工作时，随着秧箱换向，螺纹牙左、右两面交替受到压力基本相等。因此，在Ansys软件中要定义两个载荷步。载荷步1中，将载荷加在螺纹牙上表面；载荷步2中，将载荷加在螺纹牙下表面。由于载荷步1和2的加载方式完全对称，求解结果也相应对称，此处只给出载荷步1的求解结果，如图8所示。

从图8可知，在单圈螺纹牙的展开分析中，应力最大的位置处于螺纹牙两端，为337 MPa。

图7　螺纹牙有限元模型Fig.7　Finite element model of thread

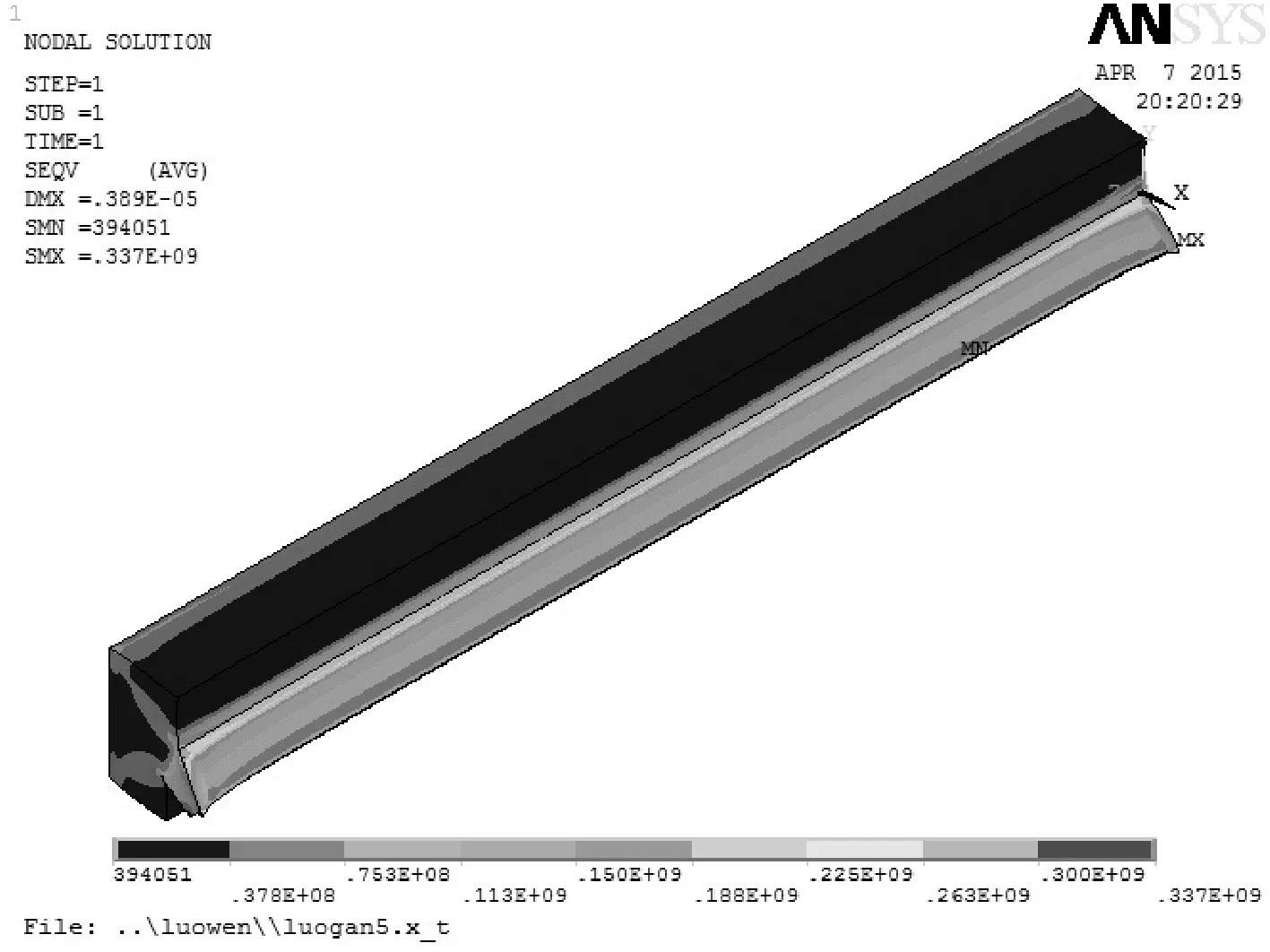
图8　范·米塞斯应力云图Fig.8　Figure of Von Mises stress

但实际情况中，丝杠与螺母旋合处的螺纹牙处于丝杠螺纹牙的中部。因此，分析时可忽略单圈螺纹牙两端的受力，对单圈螺纹牙中部进行分析，得出的结果具有代表性和可靠性。螺纹牙中部牙根处的应力大小为188 MPa，小于其屈服强度235 MPa。因此，不会发生塑性变形。

4.2螺纹牙疲劳计算

将Ansys软件静力学分析生成的两个结果文件(*.rst文件)导入Ansys/fe-safe软件中以后，需要确定螺纹牙材料的S-N曲线和载荷谱。

4.2.1螺纹牙材料的S-N曲线

Ansys/fe-safe软件通过Segger算法提供了一种方便的估算S-N曲线的方法，只需输入材料的弹性模量和抗拉强度即可。螺纹牙材料为Q235，其弹性模量为1.96e5 MPa，抗拉强度为455 MPa。

4.2.2载荷谱曲线

根据刚柔耦合分析结果，可得到螺纹牙上下两面的载荷谱，如图9所示，图中负号表示与选定正方向相反，时间节点t分别为0.083，2.834，1.417，4.251 s。

将对应的载荷谱和*.rst文件中的应力结果一起添加到疲劳分析窗口，完成其余参数设置后进行疲劳分析。

4.3螺纹牙疲劳分析结果分析

梯形丝杠螺纹牙的疲劳寿命如图10所示。与Ansys软件静力学分析同理，单圈螺纹牙两端的疲劳寿命分析不具有代表性，主要考虑单圈螺纹牙中部的疲劳寿命情况。螺纹牙在交替载荷的作用下，牙根处最容易发生疲劳破坏，疲劳破坏处的寿命N为106.65次。

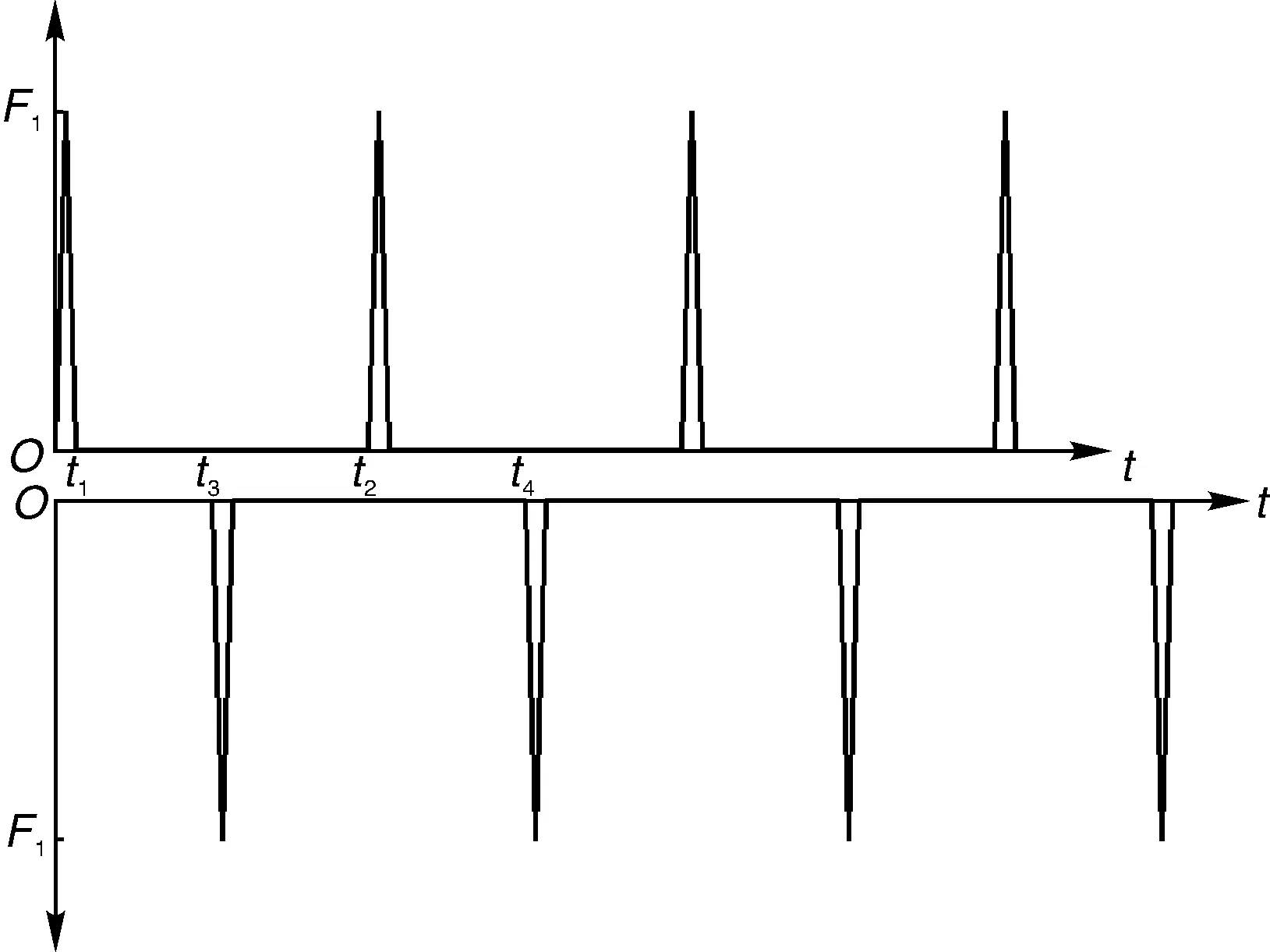
图9　螺纹牙载荷Fig.9　Load of thread

图10　螺纹牙疲劳寿命云图Fig.10　Figure of fatigue life of thread

根据秧箱实际工作情况可知，梯形丝杠螺纹牙一个受力循环时间t为2.9 s，对应的工作时长T为：

(15)

计算得T为3 598h，按插秧机每天工作12h计算，梯形丝杠螺纹牙可连续工作300d，满足插秧机工作性能要求。

5　结论

应用相关疲劳理论和方法，推导出秧箱调节机构梯形丝杠螺纹牙的疲劳寿命计算公式，并利用Adams和Ansys软件建立可调行距高速水稻插秧机秧箱的刚柔耦合模型并仿真，得到秧箱转向瞬间，梯形丝杠受到的最大轴向载荷为53.8N。

利用Ansys软件建立螺纹牙的有限元模型，并采用面压代替传统的线压，通过静力学分析得到螺纹牙最大范·米塞斯应力为188MPa，小于材料的屈服极限235MPa，不会产生塑性变形。

以静力学分析为基础，利用Ansys/fe-safe软件对螺纹牙进行疲劳分析，计算得出梯形丝杠的工作寿命为3 598h，按插秧机每天工作12h计算，梯形丝杠螺纹牙可连续工作300d，满足插秧机工作性能需求。

[1]奚小波， 张剑峰， 叶盛勇， 等. 基于ADAMS的行距无级可调钵苗栽秧机构运动仿真[J]. 中国农机化学报， 2013， 34(6): 159-162.

[2]奚小波， 张剑峰， 缪宏，等. 行距无级可调毯面钵体苗摆栽机构的设计与试验[J]. 中国农机化学报， 2014， 35(6): 4-9.

[3]赵荔， 奚小波， 赵映， 等. 行距无级可调钵苗栽秧机机架瞬态响应分析[J]. 中国农机化学报， 2013， 34(6): 77-80.

[4]赵荔，张剑峰，奚小波，等. 行距无级可调毯状钵苗栽秧机构的设计[J]. 农业装备技术，2013，39(4)：19-22.

[5]郜峰，王奇志，张行. 各向异性损伤力学在螺纹疲劳寿命预估中的应用[J]. 应用力学学报，2007， 24(1): 128-132.

[6]俞必强，李威，薛建华，等. 基于动载荷谱的齿轮弯曲疲劳寿命预测[J]. 北京科技大学学报，2013， 35(6)：813-817.

[7]KHABOUMT，BOUCHAALAN，CHAARIF，etal.Studyofaspurgeardynamicbehaviorintransientregime[J]. Mechanical Systems and Signal Processing， 2011， 25(8): 3089-3101.

[8]DIONJL，LEMOYNES，CHEVALLIERG，etal.Gearimpactsandidlegearnoise:experimentalstudyandnon-lineardynamicmodel[J]. Mechanical Systems and Signal Processing， 2009， 23(8): 2608-2628.

[9]FAGGIONIM，SAMANIFS，BERTACCHIG，etal.Dynamicoptimizationofspurgears[J]. Mechanism and Machine Theory， 2011， 46(4): 544-577.

[10]YUKSEL C， KAHRAMAN A. Dynamic tooth loads of planetary gear sets having tooth profile wear[J].MechanismandMachineTheory， 2004， 39(7): 695-715.

[11]BARAGETTI S. Fatigue resistance of steel and titanium PVD coated spur gears[J].InternationalJournalofFatigue， 2007， 29: 1893-1903.

[12]MATHIS R， REMOND Y. Kinematic and dynamic simulation of epicyclic gear trains[J].MechanismandMachineTheory， 2009， 44(2): 412-424.

[13]张文强，罗会信，党章，等. 基于ADAMS的连铸板坯摆式飞剪刚柔耦合仿真分析[J]. 武汉科技大学学报，2015， 8(4): 286-289， 306.

[14]赵丽娟，马永志. 刚柔耦合系统建模与仿真关键技术研究[J]. 计算机工程与应用，2010， 46(2): 243-248.

[15]丁九华，莫晔. 3-RPS并联机器人刚柔耦合动力学分析[J]. 沈阳大学学报(自然科学版)，2013，25(4)：307-310.

[16]钱学毅，邹丽梅，郭波，等. 滑动螺旋副螺纹牙根应力有限元分析[J]. 机械设计与制造，2006(11):132-134.

(责任编辑张韵)

Prediction of fatigue life for screw of adjustment mechanism of seedling box of adjustable spacing transplanter

ZHU De-quan1， YAO Ya-fang1， WU Li-quan2， JIANG Rui1， XIONG Wei1

(1.SchoolofEngineering，AnhuiAgriculturalUniversity，Hefei230036，China；2.SchoolofAgriculture，AnhuiAgriculturalUniversity，Hefei230036，China)

To predict fatigue life for sliding screw of adjustment mechanism of seedling box， the calculation formula of fatigue life was derived by the related theory and method. The rigid coupling model of adjustment mechanism was built with Adams and Ansys software. The real working condition of adjustment mechanism of seedling box was imitated and the axial load of screw was gained. The maximum Von Mises stress of thread was 188 MPa， which was analyzed by the finite element method based on Ansys software. The maximum Von Mises stress was less than strength limit of the material. Based on the initial conditions， fatigue life of thread was analyzed with Ansys/fe-safe software. The results showed that the working life of sliding screw was 3 598 h and met the requirements of rice transplanter.

adjustable spacing transplanter；seedling box; sliding screw; thread; fatigue life

10.3969/j.issn.1004-1524.2016.04.24

2015-08-10

国家自然科学基金项目(51403005)；国家农业科技成果转化项目(2014GB2C300002)；安徽省长三角科技联合攻关项目(1301C063006)

朱德泉(1969—)，安徽天长人，博士，教授，研究方向为机械设计理论与方法。E-mail: zhudequan@ahau.edu.cn

S223.91+1

A

1004-1524(2016)04-0693-06

朱德泉，姚亚芳，武立权，等. 可调行距插秧机秧箱调节机构丝杠疲劳寿命预测[J].浙江农业学报，2016，28(4)： 693-698.