一种等频减振设计方法及其在低地板车橡胶弹簧中的应用

刘兴起, 黄友剑

(1　乌鲁木齐铁路局　乌鲁木齐西车辆段， 新疆乌鲁木齐 830023；2　株洲时代新材料科技股份有限公司， 湖南株洲 412007)



一种等频减振设计方法及其在低地板车橡胶弹簧中的应用

刘兴起1, 黄友剑2

(1乌鲁木齐铁路局乌鲁木齐西车辆段， 新疆乌鲁木齐 830023；2株洲时代新材料科技股份有限公司， 湖南株洲 412007)

在关键承载区域橡胶弹簧系统保持近乎相同的隔振效果是设计及研发低地板车橡胶弹簧的关键技术之一。详细推导和论证橡胶弹簧在全载荷下其理想等频模型的特性曲线和基础方程，并以某型地板车橡胶弹簧为例，探讨了等频设计方法在轨道交通低地板车橡胶产品研发中的应用技术，分析结果及试验表明，基于等频设计方法确定的等频载荷区间与工程实际吻合。且此等频减振设计方法，亦可为类似橡胶减振弹簧的设计研发提供思路和借鉴。

等频减振； 低地板车； 橡胶弹簧

轨道交通橡胶弹簧的关键功能是承载和减振，承载时衰减因冲击所引起的振动，并使车辆本身的动载荷最小化，最大程度阻断振动的传递，从而确保车辆安全和平顺地行驶，以满足乘员对舒适度的高要求。而站在减振和隔振的角度，将橡胶弹簧系统设计优化出具有相对低的固有频率，那么橡胶弹簧系统就可以获得相对优良的减振和隔振效果，特别是在面对几乎所能改变的簧载范围，当簧载工况变化时，橡胶隔振系统的自振频率还能够保持不变，那么这就表明该悬架可以获得近乎完美的减振和隔振效果，而获得这种近乎完美的减振和隔振效果下的自振频率，称为理想等频[1-2]，而低地板车橡胶弹簧在设计层面必须在其关键的承载范围满足等频的设计及使用要求。因此以低地板车橡胶弹簧为例，探讨等频设计技术在橡胶弹簧中的工程化应用。

1　理想等频模型的特性曲线与基础方程

1.1基于等频减振的基础方程

低地板车橡胶弹簧在垂向承载方向可视为单自由度的振动系统，橡胶弹簧从空载到满载的整段承载过程中，其载荷位移特性曲线是连续的，基于此，为求解橡胶弹簧的弹性特性曲线，设其载荷位移特性函数表达式为：

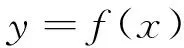
(1)

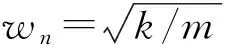
(2)

为便于方程求解，可对表征橡胶弹簧弹性特性的微分方程中的dx和y进行左右置换，同时，为求解橡胶弹簧的弹性特性曲线，特对此微分方程的两边同时取积分，即：

(3)

通过对式(3)的方程左右两边进行积分，可以导出橡胶弹簧满足理想弹性特性的对数表达式，即：

(4)

通过对式(4)的方程左右两边取指数，可求解得出橡胶弹簧满足理想弹性特性的函数表达式，即：

(5)

1.2满足等频减振的理想载荷位移特性曲线其及全载荷段方程

对于橡胶弹簧的载荷位移特性曲线来说，式(5)仅仅描述其承载段中满足等频的载荷区段，典型的载荷特性曲线将包括刚承载时的非等频段和非线性化的等频段两部分曲线；对于橡胶弹簧一条完整的载荷曲线来说，要使橡胶弹簧弹性特性的全函数表达式满足函数连续性条件，函数在非等频与等频的交接点P(x0,y0)处必须连续，即代表等频段的弹性曲线的后段函数应该与代表非等频段的弹性曲线的前段函数，其导数值和次切距应分别相等。

另外，橡胶材料虽然通常在相对小载荷的范围内，可认为是线性行为，但就其承载行为，表现出的依然是弱非线性，而且，从理论的角度上讲，弹簧无载荷即无挠度，即代表非等频段的弹性特性函数应该要过零点(0，0)，因此，其函数表达式可设置为：

(6)

函数满足连续性条件，则描述橡胶弹簧弹性特性的这两段连续函数在交接点P(x0,y0)处具有相同的切率和挠度，可以得出：

(7)

根据式(7)，可得出D值，即D=2/x0，因此，描述橡胶弹簧的后段弹性特性曲线的函数表达式为：

(8)

同时，根据两段连续函数在交接点处具有相同挠度，可以得到：c1=-2；根据设计要求，橡胶弹簧在交接点的载荷与挠度为确定值P(x0，y0)，因此，描述橡胶弹簧在等频段的函数表达式可进一步表示为：

(9)

因此描述橡胶弹簧弹性特性曲线的完整函数表达式，可通过分段函数来实现，这两段函数在交接点P(x0，y0)处实现连续，即分段函数为：

(10)

基于理想等频的承载要求，一条完整的承载曲线，可以根据式(10)分段绘制包含等频减振的载荷段和非等频减振的载荷段在内的载荷位移特性曲线(见图1)。

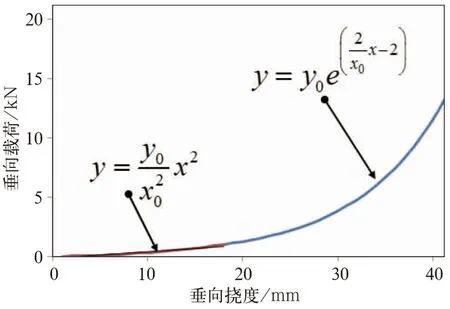
图1　基于理想等频的承载特性曲线

2　等频减振设计方法在低地板车橡胶弹簧中的应用

2.1低地板车橡胶弹簧的典型结构及承载

轨道交通低地板车所采用的橡胶减振弹簧，应用于一系悬挂，作用与空气弹簧类似，其形状类似于沙漏， 由对称的上下两瓣橡胶体组成，上下两端设置为金属垫层，中间为芯轴，用于承载车厢及以上质量。在应用时，沙漏簧承受垂向载荷，橡胶体会发生垂直方向的压缩变形，同时橡胶型面逐渐发生接触或自接触，使得承载接触面积也逐渐增大，因此沙漏簧的垂向刚度呈现出较为明显的非线性特征，其典型结构见图2所示。

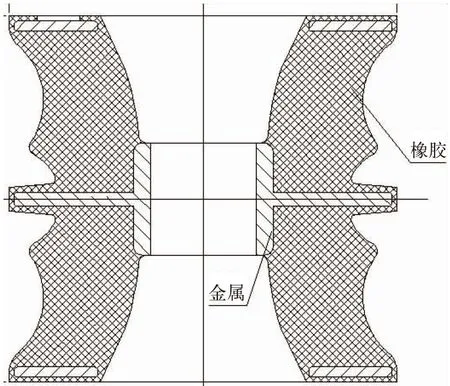
图2　低地板车沙漏橡胶弹簧

2.2橡胶材料的本构模型及其特性曲线

橡胶属于典型的超弹材料，即在任意加载类型、载荷大小作用下，均呈现为弹性特性； 且橡胶不同于金属，其拉伸、压缩和剪切特性表现为相对独立的非线性特征，因此要全面描述橡胶的力学性能，需要获取拉伸、压缩、剪切的应力应变基础试验数据[3]，并且需要选择合适的本构模型进行拟合，才能获得准确的有限元分析结果[4]。

通常采用Mooney-Rivlin模型具有较好的收敛性，且对于压缩变形量小于40%的橡胶元件具有较好的拟合精度[5]，但低地板橡胶弹簧的压缩变形量超过了60%，属于橡胶元件的大变形阶段，因此课题组选择Van der Waals 本构模型进行材料参数的拟合，图3是分析沙漏簧所用橡胶材料的试验数据，其拟合得到的材料参数见表1所示。

2.3等频减振设计方法在低地板车中的工程化应用

利用ABAUQS软件，对沙漏簧进行垂向承载分析，垂向预测结果表明：垂向方向的变形随载荷的增大而发生非线性的增加，且橡胶表面表现出严重的接触和自接触行为(见图4所示)，同时，根据有限元分析结果，橡胶整体表现出良好的应力均匀，表明沙漏簧结构具有良好的承载能力和优异的抗疲劳能力。

同时，有限元计算获得了沙漏簧产品的载荷位移特性曲线，并根据1.2节中的式(10)，绘制了理想等频承载特性曲线和试验曲线的(见图5)。根据对比结果，满足理想等频承载的区域为34～72 kN, 表明橡胶沙漏簧具有较为宽广的等频承载区间，在典型承载工况下橡胶弹簧系统能满足低地板车对隔振性能的要求。

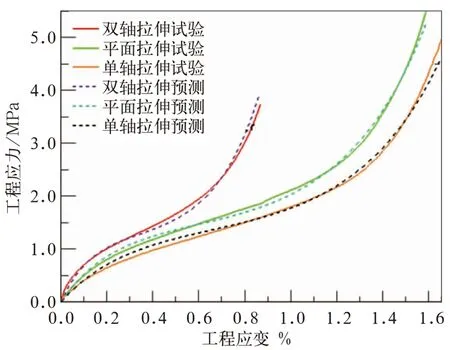
图3　橡胶材料的弹性特征曲线

超弹本构模型弹性系数VanderWaals形式Mu=1.65;Lambda_m=3.74;Alpha=1.1;Beta=7.5e-02

2.4等频减振的试验验证

为验证利用1.2节中的公式确定的等频承载区间是否满足实际隔振情况，特利用株洲时代新材料科技有限公司的多功能动态试验机进行特定承载工况下的隔振传递率试验(见图6)，试验的等效质量分别为34,45，52和70 kN，试验频率为0～8 Hz。

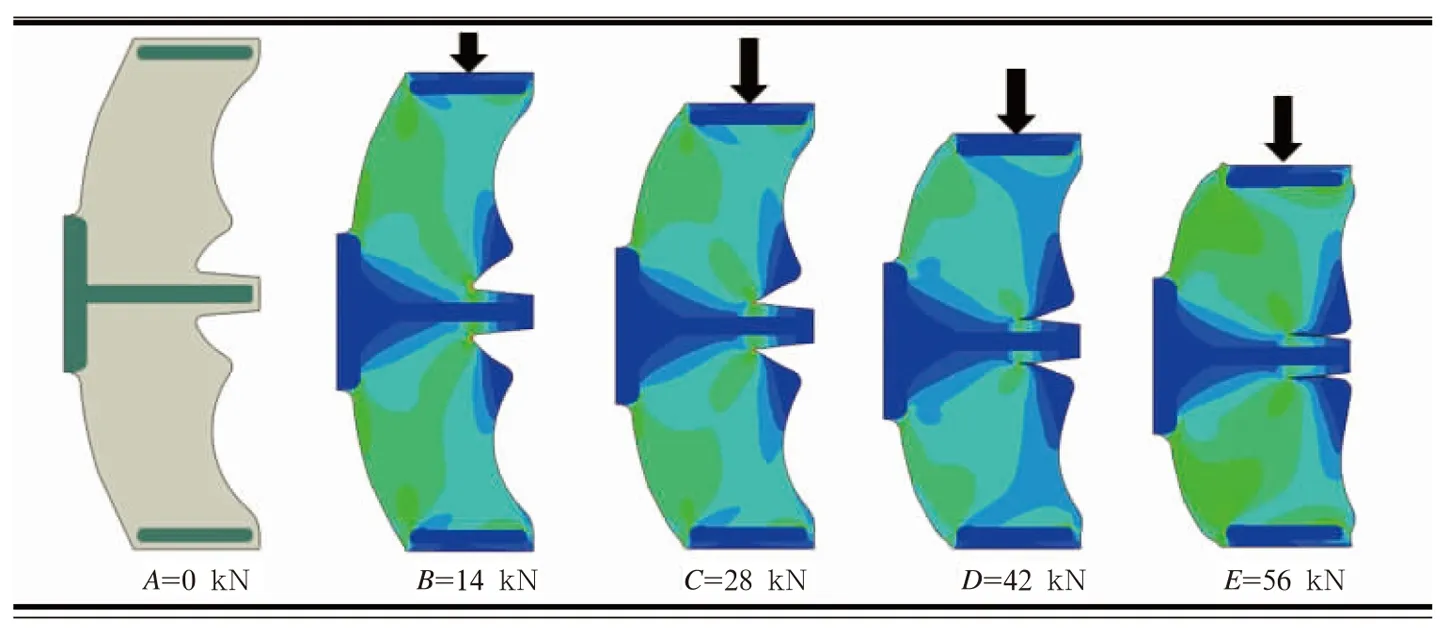
图4　沙漏簧垂向承载的变形状态

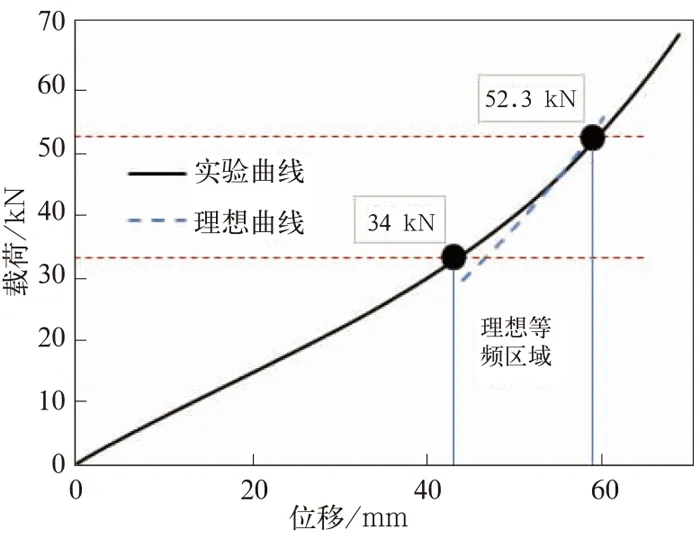
图5　沙漏簧等频减振承载区域

隔振传递率试验结果表明，各等效质量下的隔振传递率曲线基本吻合，其自振频率均少于3 Hz，且最大自振频率与最小自振频率只差仅为0.75 Hz，其意味着不同载荷间沙漏簧系统的自振频率几乎相等，亦表明橡胶沙漏簧在此承载区间具有近乎相同的隔振能力(见图7)。

3　结　论

根据低地板车橡胶沙漏簧基于等频减振的理论计算和试验验证，基本可以得出以下结论：

图6　沙漏簧隔振传递率试验

(1)结合等频减振的计算公式和载荷位移特性曲线，即可简单确定低地板车沙漏簧所具有的等频减振区域。

(2)低地板车沙漏簧在典型承载区间即34～70 kN下，其相互间的自振频率仅相差0.75 Hz，表明沙漏簧在典型承载区间具有近乎相同的隔振能力；

(3)描述等频减振的计算公式是可行的，可用于类似产品的等频减振特性的评估中。

图7　等频承载区域的隔震特性对比

[1]张亚新, 刘建勋, 黄友剑, 等. 新型复合橡胶悬架变刚度承载特性的研究[J]. 汽车技术, 2011,(5): 20-22.

[2]陈耀明. 汽车悬架论文集[M]. 苏州：苏州大学出版社, 2012.

[3]危银涛、杨挺青．橡胶类材料大变形本构关系及其有限元方法[J]．固体力学学报. 1999，20(4)：281-189．

[4]Beda T. Modeling hyper-elastic behavior of rubber : A novel invariant based and a review of constitutive models[J]. Journal of Polymer Science Part B:Polymer Physics,2007，(45):1713-1732．

[5]黄友剑，张亚新.压缩型橡胶元件的研制报告, 2007TMT-XT[R].株洲:株洲时代集团，2007：35-39.

An Equal-frequency Damping Design Method and Application in Rubber Spring of Low-floor Vehicle

LIUXingqi1，HUANGYoujian2

(1Urumqi West Car Depot, Urumqi Railway Bureau, Urumqi 830023 Xingjiang, China; 2Zhuzhou Times New Material Technology Co.,Ltd., Zhuzhou 412000 Hunan, China)

In design and research of rubber spring of low-floor vehicle, it is a key technology that rubber spring keeps almost equal damping effect in important loading area. In this paper, characteristic curve and fundamental equation of ideal equal-frequency model is derived and verified for rubber spring under full load. By taking the rubber spring of certain a floor vehicle as a sample, the application technology of equal-frequency design method is specifically discussed in the field of research and development of rubber products of low-floor vehicle. It is indicated by analysis result and test result that the equal-frequency load amplitude determined by equal-frequency design method complies with engineering application. The equal-frequency design method can be used as a reference to design and research & development of similar rubber damping products.

equal-frequency damping; low-floor vehicle; rubber spring

1008-7842 (2016) 04-0061-04

��)男，工程师(

2016-03-16)

U270.34

Adoi:10.3969/j.issn.1008-7842.2016.04.15