匀速运动目标长时间积累检测中的解距离模糊算法研究

张杨梅，冯西安

(西北工业大学航海学院，陕西西安 710072)

匀速运动目标长时间积累检测中的解距离模糊算法研究

张杨梅，冯西安

(西北工业大学航海学院，陕西西安 710072)

针对匀速运动目标在多脉冲长时间积累检测体制下会出现的距离走动及距离模糊问题，考虑目标运动对解距离模糊的影响，将运动目标的速度参数引入同余方程组，建立了包含目标运动参数的多重脉冲重复周期回波模型，并提出了一种基于距离走动校正的解匀速运动目标距离模糊算法。该算法利用多重脉冲重复周期对运动目标进行参数估计，采用传统解模糊算法重构出带有误差的目标距离，利用脉冲重复周期之间的相互关系，校正由于目标运动而引起的目标距离估计误差，得到目标在每个脉冲重复周期中的真实距离。仿真实验表明，所提算法能够有效计算出目标距离并估计出目标运动速度，在目标模糊距离存在测量误差时也能够较为精确地估计出目标的运动参数。

长时间积累；匀速运动；距离模糊；距离单元走动

目前，声呐系统中常采用重复发射脉冲信号，并利用接收回波与发射脉冲信号间的时间差来进行测距。在这种多脉冲检测体制下，信号积累技术常被用来提高声呐的微弱目标检测能力。然而，当目标回波的传播时延大于脉冲重复周期时，将会产生距离模糊。同时，随着脉冲积累时间的增加，由于声呐平台与目标之间的相对运动，脉冲回波在慢时间维上将不再处于同一个快时间维距离单元内，而是在不同的快时间维距离单元内走动。如果不考虑目标回波的跨距离走动和跨脉冲重复周期的距离模糊，就无法有效地利用信号能量，从而无法实现回波脉冲的有效积累检测和目标真实距离的判定。

解距离模糊的方法主要有信号处理法、中国余数定理(Chinese remainder theorem，CRT)、排列组合方法、多假设目标跟踪方法、稀疏重构法、运动累积测距法和滤波法等。其中，CRT由于其计算简单，运算速度快而成为一种最常用的解模糊方法。但是，传统CRT的输入和输出均为整数，无法应用在实数域，且对余数的误差非常敏感。因此，目前对CRT类算法的改进和优化基本上都是用来解决实数输入值以及测距误差所导致的真实距离重构误差的［1-7］。戴文琪等明确指出测距误差主要是指由于杂波和噪声干扰以及目标运动等因素所引起的测量误差［1］，并在文献［2］中提出一种具有纠错能力的解模糊算法，通过纠错数对有重构误差的重构数进行纠错，纠错后的剩余误差与余数的误差精度相同。文献［3-7］研究了稳健的CRT重构算法，采用一组非互质的模数及相应的有误差的余数来估计整数。文献［3-4］将其扩展到实数域。文献［5］提出一种多阶的CRT算法，扩大了模数的取值范围。文献［6］提出一种基于最大似然估计的CRT算法，能够在余数误差服从缠绕高斯分布的情况下对实数进行重构。文献［7］使用点阵理论来估计距离。这些优化改进算法将目标运动所引起的目标距离变化归纳到了测量误差中，认为待重构的目标距离为某一未知整数。然而，匀速运动的目标在每一个探测周期内所处的距离单元有可能是不相同的，可能是一系列距离值Ri(1≤i≤k，k为脉冲重复周期个数)。在这种情况下，解距离模糊算法就不再是对一个未知数进行重构，而应是对一系列未知数进行重构，继续使用CRT算法将会产生较大的误差。

本文根据长时间积累检测中存在的距离模糊和回波脉冲跨距离单元走动问题，针对匀速运动目标，考虑目标运动对CRT类算法所产生的影响，建立了匀速运动目标多脉冲重复周期的探测回波模型，分析了目标运动速度、脉冲波速、脉冲重复频率以及目标距离变化率之间的相互关系，并提出一种基于距离走动校正的解匀速运动目标距离模糊算法。该算法利用一组数值非互质但满足一定条件的脉冲重复周期(pulse repetition time，PRT)对运动目标进行距离测量，得到一组相应的模糊距离；利用已有的CRT算法重构出目标距离，由于这一重构结果是在忽略由目标运动而引起的目标跨距离单元走动的基础上得到的，此时得到的目标距离是有重构误差的；纠正由距离单元走动带来的目标距离重构误差，得到目标在每个PRT的真实距离，并计算出目标的运动速度。仿真实验表明，本文所提算法在参数配置适当的情况下能够计算出目标距离并估计目标运动速度，在目标模糊距离存在测量误差时也能够较为精确地估计出目标的运动参数，从而校正运动目标的跨距离单元走动，实现目标回波脉冲的有效积累。

1　匀速运动目标多重脉冲重复周期探测回波模型

设目标在距离声呐R处，以速度v做匀速运动，定义声呐与目标之间延长线方向为正方向。交替使用k重不同PRT探测目标，k个PRT分别为Tr1，Tr2，…，Trk，脉冲宽度Tp，各PRT内所包含的距离单元数分别为m1，m2，…，mk，m1＜m2＜…＜mk，且mi＝floor(Tri/Tp)，i＝1，2，…，k，floor(·)表示向下取整运算。令x＝2R/cTp，则有以下关系

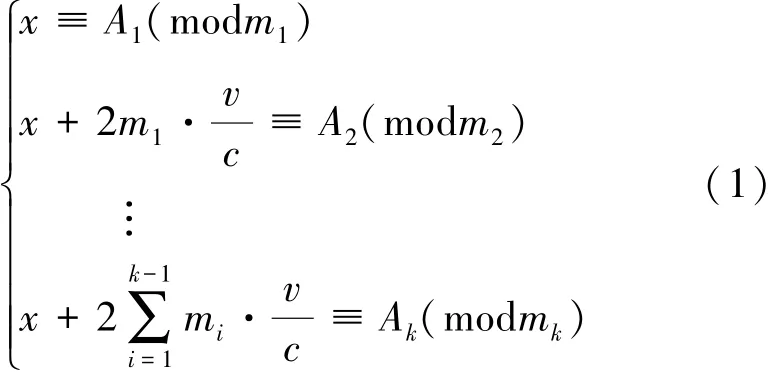
式中，Ai以距离单元为单位，为第i个PRT测出的模糊距离，Ni为正整数，c为水中声速。

当目标与声呐之间无相对运动(v＝0)时，各重复周期之间无跨距离单元走动，(1)式可改写为

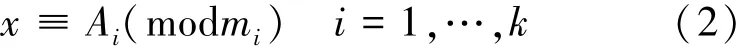
1)m1，m2，…，mk两两互质时，x可以由(3)式计算得到：

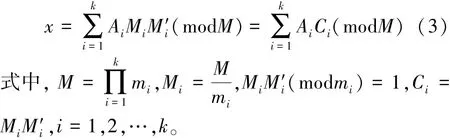
2)m1，m2，…，mk不是两两互质时，可由(4)式估计x［3］

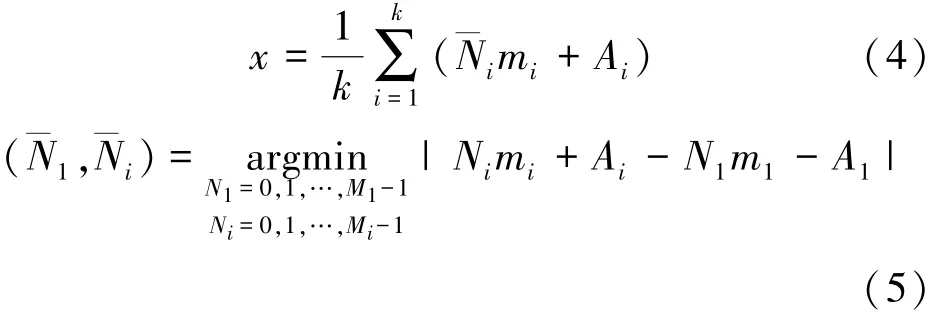
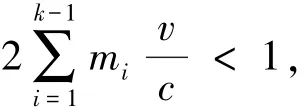
2　匀速运动目标的解距离模糊算法

2.1基于距离走动校正的解匀速运动目标距离模糊算法

式中，N1，N2，…，Nk为各脉冲周期的模糊数。若从(6)式中取出第i个和第i＋1个同余式，并以第i个脉冲重复周期中目标所在位置做为参考点，可组成同余式组(7)

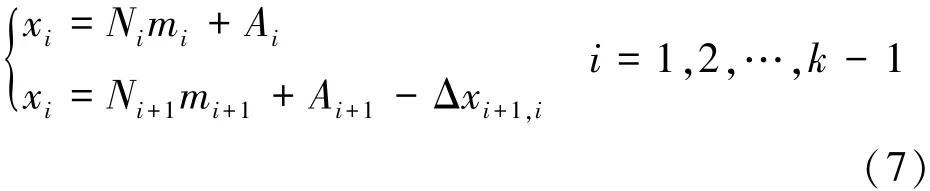
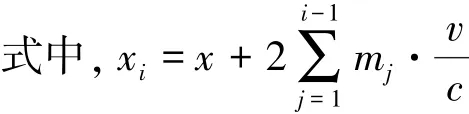
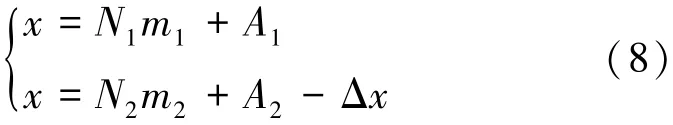
以下推导均以(8)式为基础。

设N2＝N1－p，p为整数。若Δx＝0，即相邻的2个脉冲重复周期之间目标无运动，则N1≥N2，且p的取值范围为p＝0，1，2，…，N1；若Δx≠0，即相邻2个脉冲重复周期之间目标有运动，此时N2有可能大于N1，p的取值范围为p＝－1，0，1，2，…，N1。令d＝gcd(m1，m2)，Γi＝mi/d，i＝1，2，m1：m2＝Γ1：Γ2＝Q：Q＋P，将其带入(8)式可得

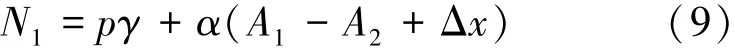
式中，γ＝(Q＋P)/P，α＝Q/(Pm1)。可以看出，N1为p的函数，可将N1表示为N1(p)。由于(8)式中的模糊数N1应为整数，因此必有p＝pT使得N1(pT)的值为整数，此时，N1(pT)即为(8)式中N1的模糊数解N′1

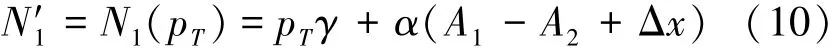
若忽略Δx，则(8)式变为：

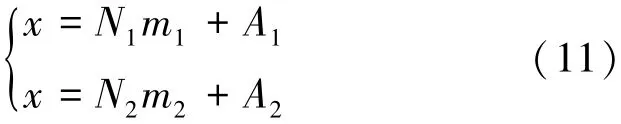
此时，求解N1的表达式由(9)式变为

忽略Δx对同余方程组的影响，将使得N1(pT)的值不再为整数，而使得N1(p)为整数的p值将发生在

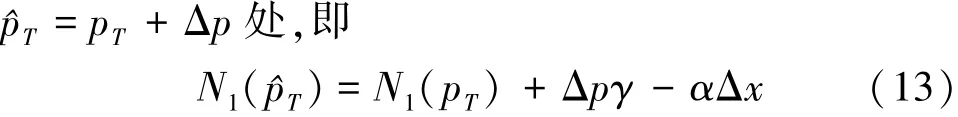
因此，(11)式中N1的模糊数解N＾′1为

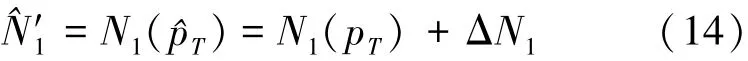
式中，ΔN1表示求解x时由于忽略Δx而引起的模糊数解的增量值，且

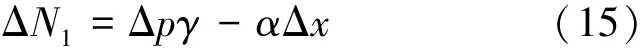
则不考虑Δx引起的影响而直接由(11)式计算得出的x′为

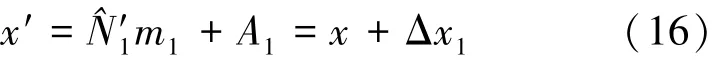
式中，Δx1＝ΔN1m1是由于忽略目标运动的影响而引起的x的估计误差。则，(8)式中x的真实值应为

为了能纠正距离单元走动而带来的目标距离估计的误差，应使｜αΔx｜≪1，即

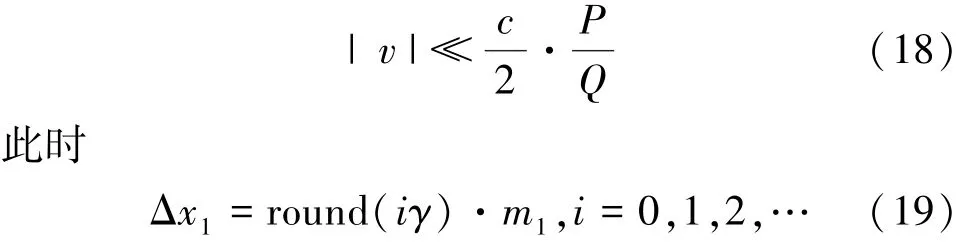
式中，round(·)表示四舍五入运算。

则，对匀速运动目标进行解距离模糊并测速的步骤如图1所示。

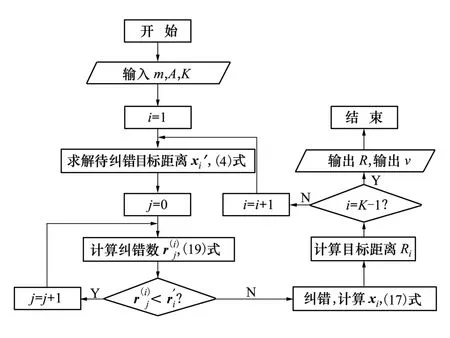
图1　算法流程框图

Step1 从同余式组(6)的k个同余式中依次取相邻的2个同余式组成k－1个同余式组：

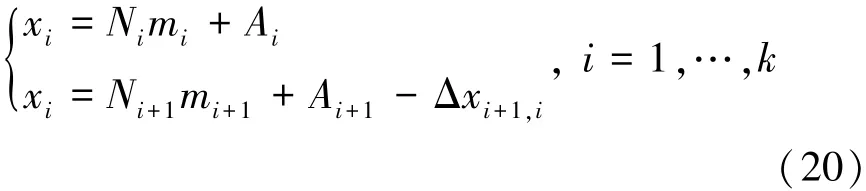
Step2 利用(20)式中所列的k－1个同余式组依次求解xi，i＝1，2，…，k－1；

substep1 将x′i看做是忽略Δxi＋1，i的影响而计算得到的带有误差的目标距离，利用(4)式求解同余式组：

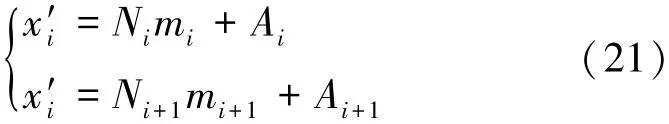
substep5 计算目标距离Ri＝xi·cTp/2。

Step3 使用(22)式估计每个PRT内目标运动速度vi，i＝1，2，…，k－2；

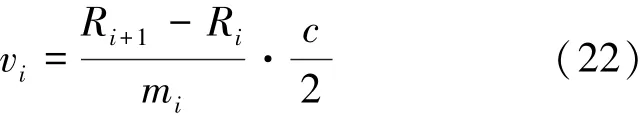
Step4 由于目标匀速运动，因此计算得到的k－2个vi的值应近似相等。定义

则目标的运动速度v可由下式估计得到

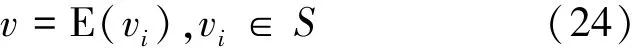
式中，E(·)表示期望。

2.2算法误差分析

1)无噪声干扰情况

由上式可知，在两两互质的Γi确定的情况下，最大公约数d越大，Δv越小。

为了能够较为准确地估计出目标的运动速度，需要使｜Δv｜≪1，即满足

2)有噪声干扰情况

噪声干扰下，设测得的模糊距离存在误差ΔAi，即由文献［8］可知，若｜ΔAi｜≤ε，则当d＞4ε时，通过(4)式计算得到的x′i也存在估计误差Δx′i，且其上限为

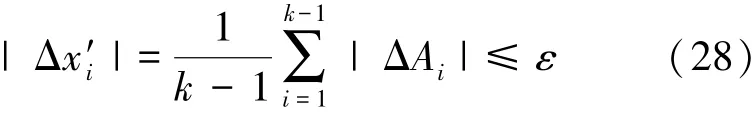
为了能够纠正测量误差及目标运动而带来的距离估计误差，v与mi之间应满足

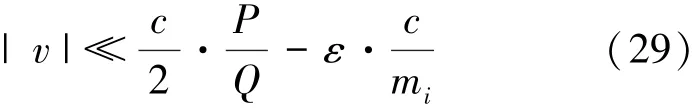
此时，目标距离的估计误差｜Δxi｜≤ε，速度估计误差｜Δvi｜≤c·ε/mi。为了能够较为准确地估计出目标的运动速度，需满足

3　仿真结果与分析

下面分别从无噪声干扰情况和有噪声干扰情况入手，对本文所提算法进行仿真实验，并给出了仿真结果，分析了mi的取值对算法性能的影响，从而验证本文算法的合理性及科学性。

3.1无噪声干扰情况下d对算法性能的影响

以三重PRT系统为例，设目标速度v的范围为－30～30 m/s，目标初始距离1 700个距离单元，Γ1＝139，Γ2＝181，Γ3＝229，d分别取4、10、20。

d＝10时的测距结果如表1所示，并与文献［5］所提的闭式RCRT算法进行了比较。本文算法能够正确地重构出每个PRT内目标所在的距离单元，测距误差为使用测量值进行计算的四舍五入误差。而闭式RCRT只能在v＝0时正确估计目标距离，当v≠0时，测距误差相当大。这是由于在目标匀速运动的情况下，各重复周期之间目标距离的变化较大，若将每周期内的跨距离单元走动看作是测量误差，已经超过了闭式RCRT所要求的余数误差小于d/4的前提条件，因此无法准确重构出目标的距离。

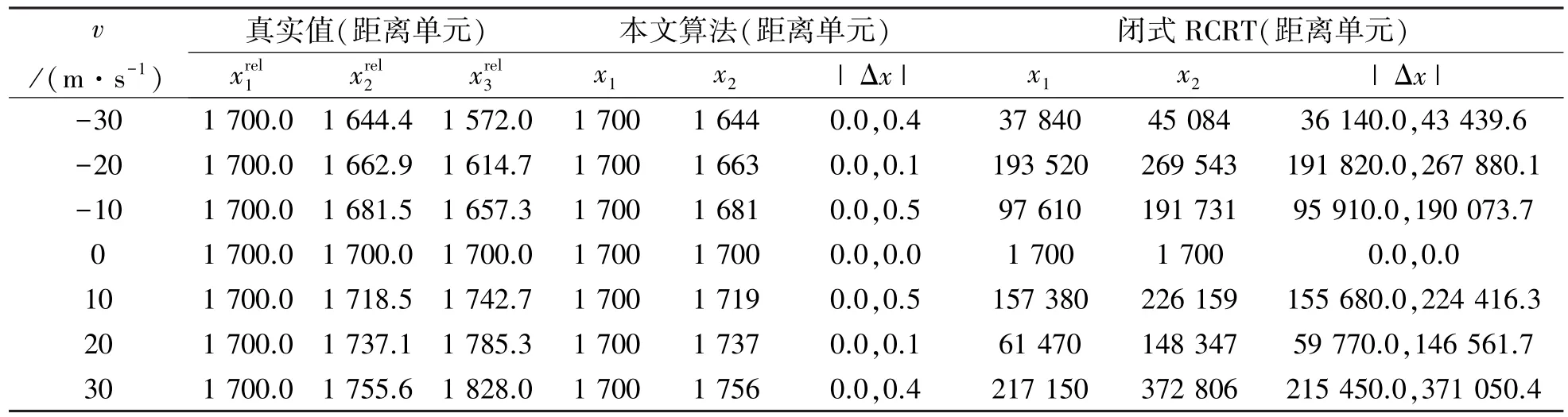
表1　d=10时的仿真测距结果

测速结果如图2所示。

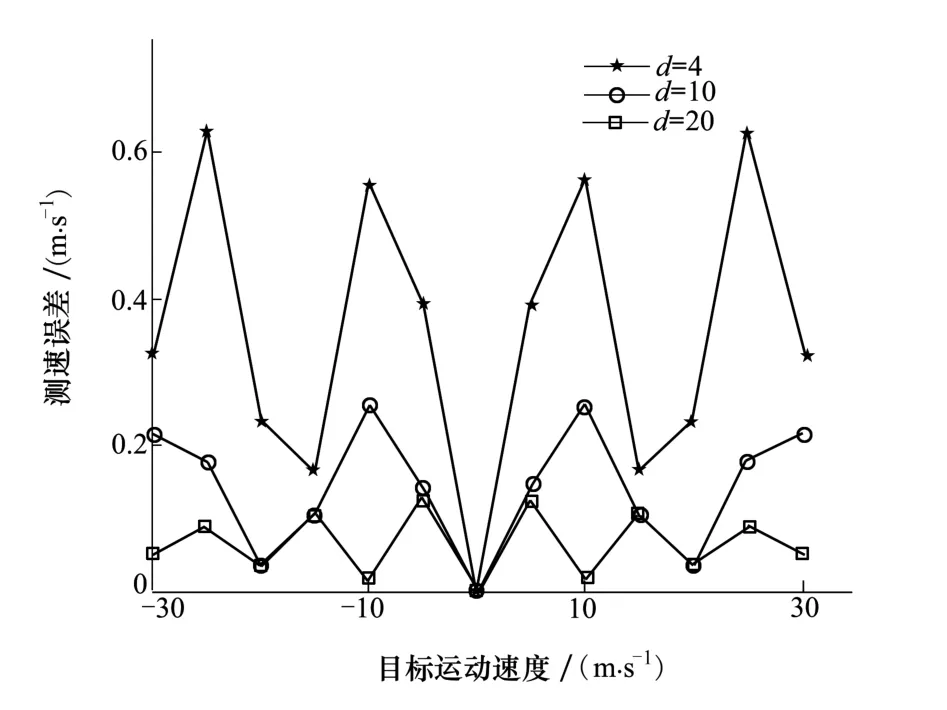
图2　目标运动速度对测速误差的影响

3.2无噪声干扰情况下目标初始距离R对算法性能的影响

设目标速度分别为1 m/s、2 m/s和10 m/s，目标初始距离分别为1 000、1 001、1 002个距离单元，在无噪干扰情况下使用m1＝1 390、m2＝1 810、m3＝2 290探测目标，测距结果如表2所示。本文所提算法能够正确估计出目标在每个周期的距离，测距误差为计算时的四舍五入误差。由于在3.1节中已经通过仿真说明了闭式GRCRT无法解决运动目标的模糊问题，因此本节仅对本文所提算法进行了仿真。

由(26)式可知，无噪声干扰情况下，Δv与目标运动所引起的距离门走动归一化时的四舍五入误差大小有关。因此在目标运动速度v一定的情况下，目标初始所在的距离单元x对Δv无影响。

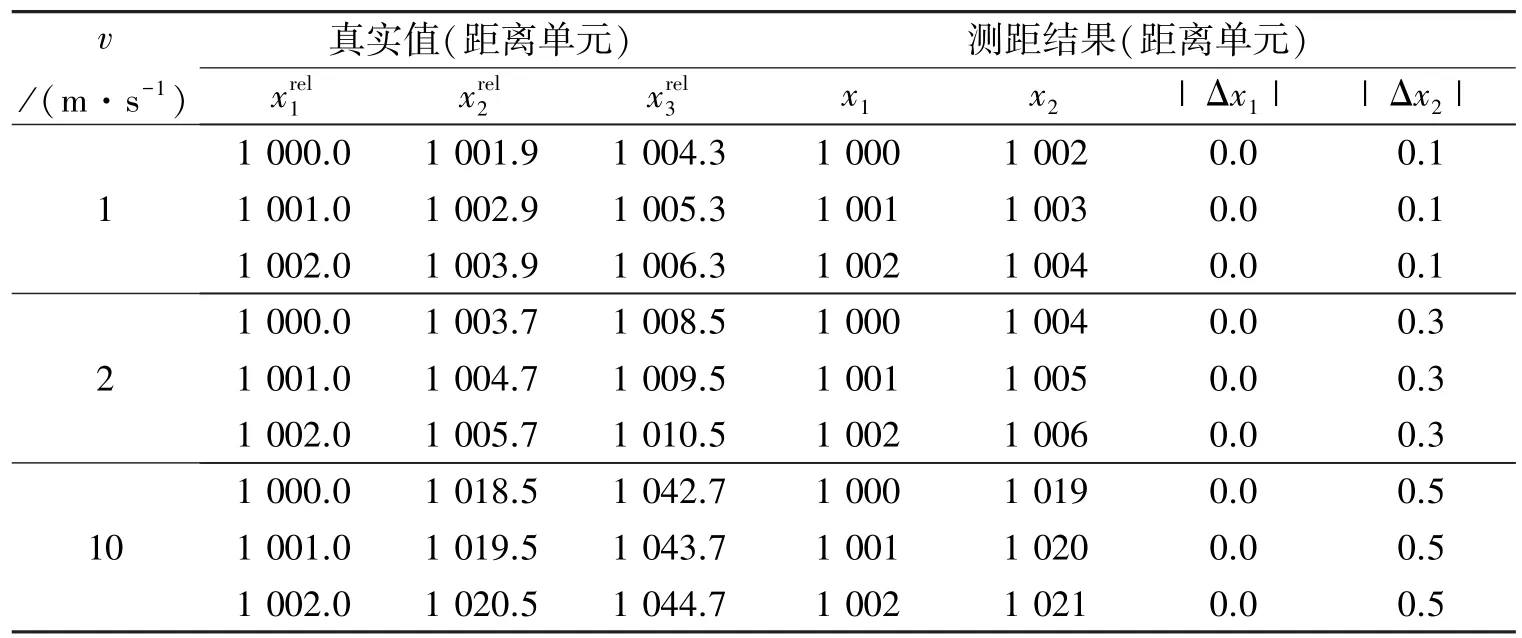
表2　不同目标初始距离下的仿真测距结果

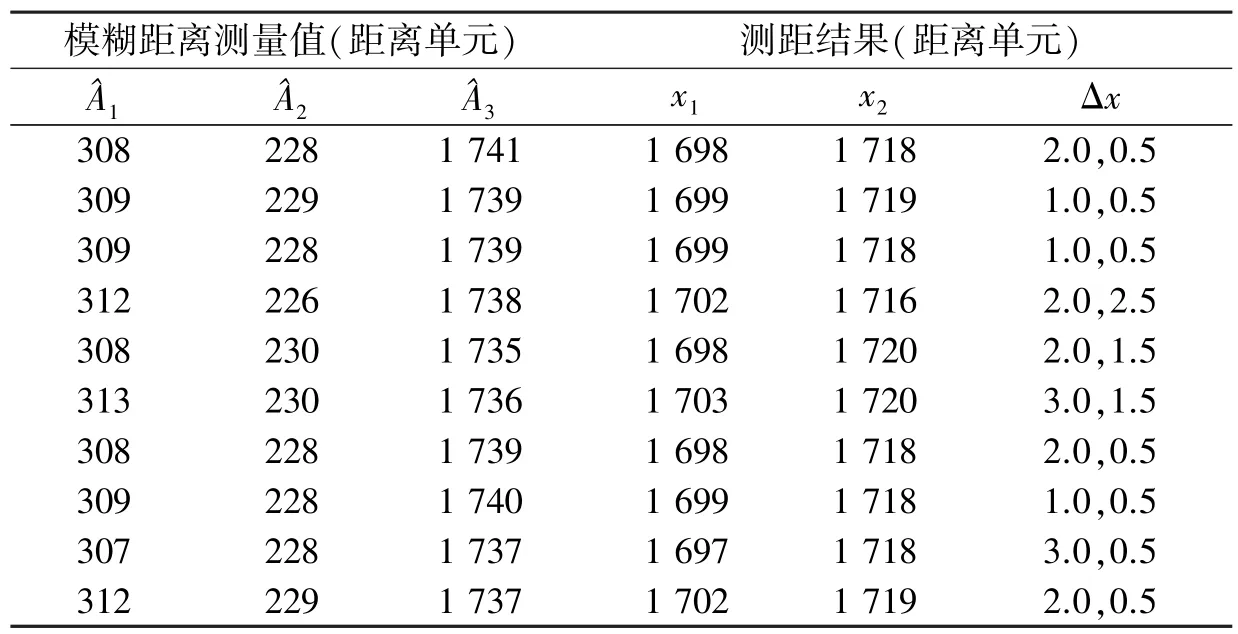
表3　噪声干扰下的仿真测距结果

3.3有噪声干扰情况下测量误差对算法性能的影响

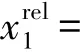
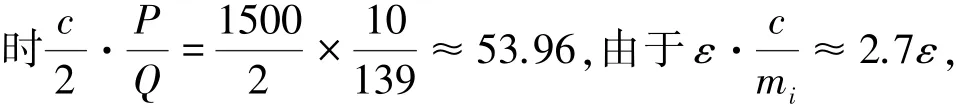
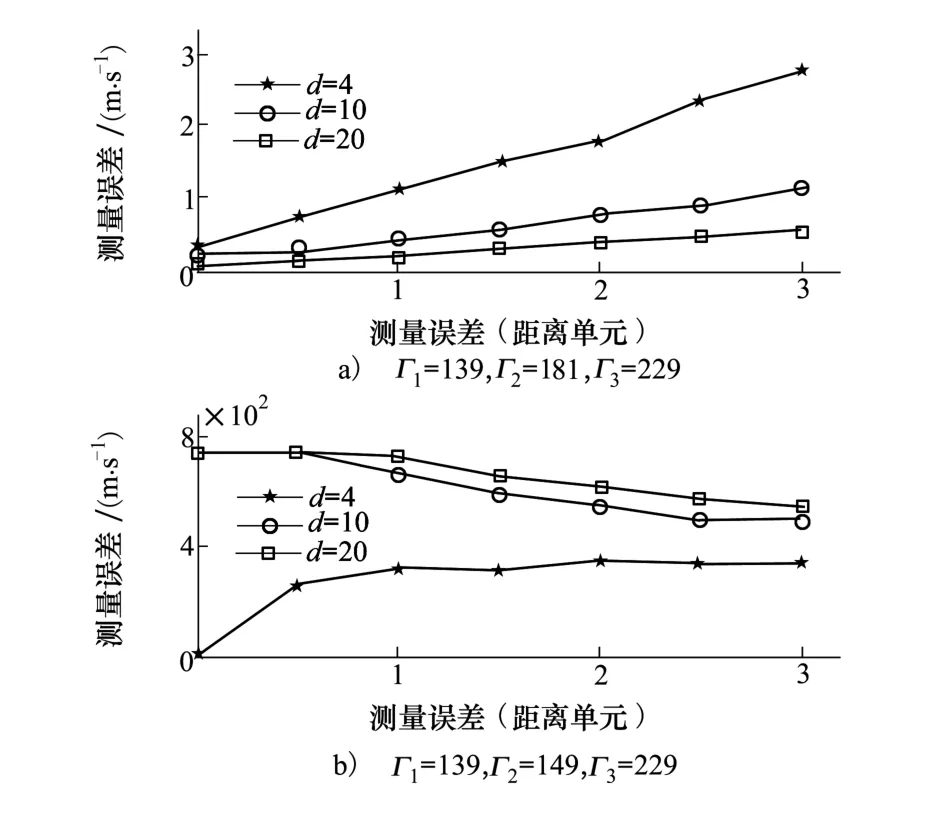
图3　测量误差对测速误差的影响

4　结 论

通过延长信号积累时间，水下主动声呐系统可以提高微弱目标检测能力，并完成目标与声呐间径向速度的提取。但是，长时间积累也带来了一些新的技术问题，主要是在积累时间内目标回波有可能发生距离模糊和距离走动。为此，本文对匀速运动目标的多重脉冲重复周期探测回波进行建模，并提出一种基于距离走动校正的解匀速运动目标距离模糊算法。该算法考虑目标运动对多重PRT探测性能所产生的影响，在利用已有CRT算法计算得到带有重构误差的目标距离后，通过公式纠正由于目标运动带来的目标距离估计误差，得到目标在每个脉冲重复周期的真实距离，并计算出目标的运动速度。数值仿真结果表明，本文所提算法能够在存在距离模糊和距离走动的情况下估算出待测目标的运动参数，实现运动目标检测中的解距离模糊和距离走动补偿。

［1］ 戴文琪，王家隆，曾建瑜.余数法解距离模糊的检错、纠错条件［J］.电子学报，1988，16(6)：93-98

Dai Wenqi，Wang Jialong，Zeng Jianyu.The Error Detecting and Error-Correcting Conditions of the Range Ambiguities Solved by Chinese Remainder Theorem［J］.Acta Electronica Sinica，1988，16(6)：93-98(in Chinese)

［2］ 戴文琪，赵问道.具有纠错能力的解距离模糊的模糊数法［J］.电子学报，1991，19(2)：127-129

Dai Wenqi，Zhao Wendao.The Methods Having Error Correcting Ability to Solve the Range Ambiguities［J］.Acta Electronica Sinica，1991，19(2)：127-129(in Chinese)

［3］ Li X，Liang H，Xia X G.A Robust Chinese Remainder Theorem with its Applications in Frequency Estimation from Undersampled Waveforms［J］.IEEE Trans on Signal Processing，2009，57(11)：4314-4322

［4］ Wang Wenjie，Xia Xianggen.A Closed-Form Robust Chinese Remainder Theorem and its Performance Analysis［J］.IEEE Trans on Signal Process，2010，58(11)：5655-5666

［5］ Xiao L，Xia X G，Wang W.Multi-Stage Robust Chinese Remainder Theorem［J］.IEEE Trans on Signal Processing，2014，62 (18)：4772-4785

［6］ Wang W J，Li X P，Wang W，et al.Maximum Likelihood Estimation Based Robust Chinese Remainder Theorem for Real Numbers and Its Fast Algorithm［J］.IEEE Trans on Signal Process，2015，63(13)：3317-3331

［7］ Li Wenchao，Wang Xuezhi，Wang Xinmin，et al.Distance Estimation Using Wrapped Phase Measurements in Noise［J］.IEEE Trans on Signal Process，2013，61(7)：1676-1688

［8］ 梁红，张琦，杨长生.广义稳健的中国剩余定理及其在欠采样率下频率估计中的应用［J］.电子与信息学报，2010，32 (8)：1802-1805

Liang Hong，Zhang Qi，Yang Changsheng.A Generalized Robust Chinese Remainder Theorem and its Application to Frequency Estimation with Undersampling［J］.Journal of Electronics＆Information Technology，2010，32(8)：1802-1805(in Chinese)

Resolving Range Ambiguity in Long Time Accumulation Detection of Target Moving with Uniform Velocity

Zhang Yangmei，Feng Xi′an
(College of Marine Science and Technology，Northwestern Polytechnical University，Xi′an 710072，China)

Long time accumulation method is a commonly used technique to detect weak target.But ambiguities may arise in both range and Doppler measurements.Furthermore，the presence of target motion causes the migration of echo envelope within multi-cycle integration time and severely affects the detection performance.For locating moving target，we establish a multi-pulse echo model based on multiple-burst sonar signal and present a range ambiguity resolving algorithm based on correcting range cell migrations.Through utilizing a set of pulse repetition intervals(PRIs)that are not pair-wisely co-prime，we design the algorithm to recover the correct position and speed of the target moving with uniform velocity.Traditional ambiguity resolving method is used to obtain a preliminary target range，which is incorrect in the case of moving target.The proposed method corrects the reconstruction errors by evaluating the relationships among PRIs.Numerical simulation results and their analysis show preliminarily that the proposed algorithm performs well in estimating target range and velocity despite unavoidable measurement errors.

algorithms，calculations，computer simulation，design，Doppler effect，fuzzy systems，mathematical models，measurement errors，Monte Carlo methods，range finding，sonar，target tracking，time delay， velocity；CRT(Chinese Remainder Theorem)，long time accumulation，migration through range cell， PRT(Pulse Repetition Time)，range ambiguity，uniform motion

TN911

A

1000-2758(2016)02-0194-07

2015-09-02基金项目：国家自然科学基金(61271414)与陕西省自然科学基金(2014JM2-6090)资助

张杨梅(1982—)，女，西北工业大学博士研究生，主要从事水声信号处理、水下目标探测的研究。