空间数据库中基于Voronoi图的组反k最近邻查询*
张丽平,刘 蕾,李 松,于嘉希
哈尔滨理工大学 计算机科学与技术学院,哈尔滨 150080
空间数据库中基于Voronoi图的组反k最近邻查询*
张丽平+,刘蕾,李松,于嘉希
哈尔滨理工大学 计算机科学与技术学院,哈尔滨 150080
为了改进现有的组反k最近邻查询算法的查询速度与准确度,提出了一种基于Voronoi图的组反k最近邻查询方法(group reverse k nearest neighbor guery method based on Voronoi diagram,V_GRkNN)。该方法获得的结果集是将这组查询点中任意一点作为kNN的数据点集合,在实际应用中可以用来评估一组查询对象的影响力。该方法的特点是首先对查询点集Q进行优化处理,降低查询点数量对查询效率的负面影响;接着对数据点集P进行约减,缩小查询搜索范围;然后根据基于Voronoi图的剪枝策略对候选集进行过滤;最后经过精炼获得GRkNN查询的结果集。该方法在数据集处理阶段很大程度上提高了查询速度,在过滤、精炼阶段利用Voronoi图的特性提高了查询的准确性。理论研究和实验表明,所提方法的效率明显优于可选的已有方法。关键词:Voronoi图;反k最近邻;组反k最近邻;索引结构
1 引言
随着基于位置服务技术的广泛应用,最近邻(nearest neighbor,NN)[1]查询成为空间数据库查询中的热点问题。近年来,最近邻查询的研究进一步拓展到针对受限区域内的最近邻查询[2]、反向最近邻查询[3]、组最近邻查询[4]、可视最近邻查询[5-6]、连续可视反向最近邻查询[7]、不确定数据集中的k最近邻查询[8]、强邻近对查询[9]、双色数据集上的反向最近邻查询[10]、不确定移动对象的查询[11]等方面,所取得的成果解决了最近邻查询领域的一系列重要问题。
k最近邻(k nearest neighbor,kNN)查询是空间数据库中的最重要查询之一。反k最近邻(reverse k nearest neighbor,RkNN)[12]查询是k最近邻查询的一个重要变体,获得将查询对象作为k最近邻的数据对象集合。RkNN查询一般用来评估查询对象的影响力,从而反映查询点对哪些空间数据点影响较大。由于此类查询可以支持高级的分析和预测应用,在实际应用中已经变得越来越重要。例如,在一家商场的选址工作中,需要评估该商场对附近哪些人群有影响力,该商场所吸引的顾客群就是RkNN查询所要找的影响集。根据实际需求,有时需要对一个商业区进行影响力评估,也即查询一组查询对象的RkNN结果,因此文献[13]提出了组反k最近邻(group reverse k nearest neighbor,GRkNN)查询。GRkNN查询在空间数据库中有着重要的实际应用意义。
对于组最近邻(group nearest neighbor,GNN)查询,文献[4]给出了3种算法:MQM(multiple query method)、SPM(single point method)和MBM(minimum bounding method)。其中MQM利用阈值算法的思想,增量计算查询点集Q中每个点的NN,并在这些NN中找到最终结果。该方法对每个点进行处理,查询点的搜索区域有很大重叠性,效率较低。SPM首先计算Q的质心q,然后通过遍历R-树找到结果,利用q进行剪枝。该方法将查询点集用一个代表点q表示,可以避免许多冗余操作,化繁为简,较快地查询到结果,但是只适合查询点较聚集的情况。MBM也是通过遍历R-树找到结果,但利用Q的最小外包矩形(minimum bounding rectangle,MBR)进行剪枝。随着数据集增大,该算法动态更新的时间复杂度较高。孙冬璞等人提出基于VTree索引的组最近邻查询的VGNN算法[14]。Li等人提出基于Q中两种最远点构成的椭圆及其MBR进行剪枝的GNN方法[15]。对于RkNN查询,Stanoi等人提出了60度剪枝法,将空间划分成6等份,然后在每个区域中,对查询点q的第k个最近邻以外的区域进行剪枝,未被剪枝的数据点就是RkNN查询的候选点[16]。Tao等人提出TPL剪枝法,该方法比60度剪枝法具有更强的剪枝能力[17]。Wu等人在TPL剪枝方法的基础上提出了INCH(intersectionsƳ convex hull)空间缩减法[18]。宋晓宇等人提出了组反k最近邻查询[13],通过计算查询对象的最小覆盖圆,将圆中的对象作为一个整体来计算该组查询点RkNN的搜索区域。该算法在查询效率方面有待提高。
为了更有效地解决组反k最近邻查询问题,本文提出了一种高效的基于Voronoi图[19]的组反k最近邻查询方法(group reverse k nearest neighbor query method based on Voronoi diagram,V_GRkNN)。该方法获得的结果集是将这组查询点中任意一点作为kNN的数据点集合,在实际应用中可以用来评估一组查询对象的影响力。该方法包括4个过程:优化查询点集,约减数据点集,剪枝过程,精炼过程。首先快速获得查询点集Q的质心q,用质心q近似地代表查询点集整体即可有效地避免搜索区域频繁重叠的情况,从而提高了查询效率。然后对数据点集进行约减,得到初步的候选集合,再利用剪枝策略对候选集合中的点进行剪枝。最后利用公式进行排错处理,得到精确的结果集。利用Voronoi图的邻接特性可以在约减数据点集阶段和过滤阶段有效地过滤掉大量的非候选者,快速地缩小查询范围,提高整个算法的查询效率。基于以上分析,本文提出的基于Voronoi图的组反k最近邻查询方法在数据集处理阶段很大程度上提高了查询速度,在过滤、精炼阶段利用Voronoi图的特性提高了查询的准确性。
2 基础定义与定理
Voronoi图是组反k最近邻查询所使用的重要数学工具,首先给出Voronoi图的基本定义及性质。
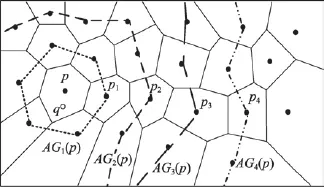
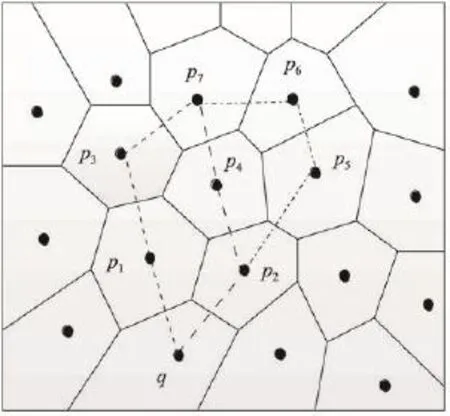
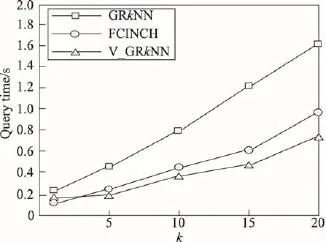
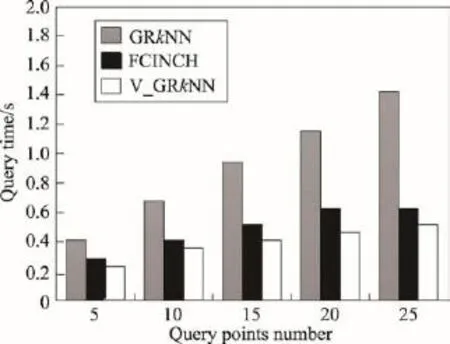
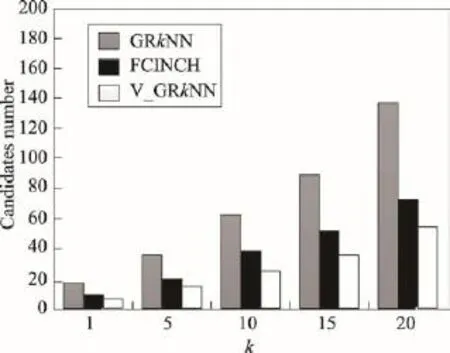
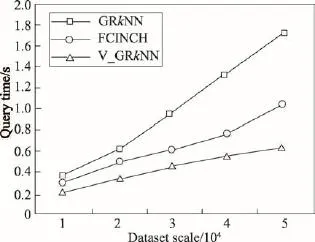
定义1(Voronoi图[19])给定一组生成点P={p1, p2,…,pn}⊂R2,其中2 定义2(Voronoi图的k级邻接生成点[19])给定一组生成点P={p1,p2,…,pn}⊂R2生成的Voronoi图中,其中2 (1)1级邻接生成点 AG1(pi)={pj|VP(pi)和VP(pj)有公共边} (2)k(k≥2)级邻接生成点 AGk(pi)={pj|VP(p)和VP(pj)有公共边,p∈AGk-1(pi)} 由Voronoi图的结构及定义可得出以下基本性质。 性质1(最近邻近特性[19])生成点pi的最近邻在pi的邻接生成点之中。 性质2(局域动态特性[19])每个Voronoi棱由2个Voronoi多边形所共享,而每个Voronoi多边形的棱的平均数目最多是6,因此每个生成点最多有6个邻接的生成点。 下面给出3个由Voronoi图的基本性质得出的定理,这些定理为界定组反k最近邻查询的查询范围提供了理论依据。 定理1[19]点q为Voronoi单元VP(pi)内任一点,pk+1∈AGk+1(pi),那么必存在一点 pk∈AGk(pi)使得dist (q,pk)≤dist(q,pk+1)。 定理2[19]对于Voronoi多边形VP(pi)内任一点q,q到pi的k级邻接生成点的最小距离小于到任何pi的k+1级邻接生成点的距离(k为整数,k≥1)。 定理3[19]对于Voronoi多边形VP(pi)内任一点q,q的第 k+1个最近邻qk+1,有qk+1∈AG1(p)⋃AG2(p)⋃…⋃AGk(p)(k为整数,k≥1),即q的第k+1个最近邻在q的最近邻前k级邻接生成点中。 下面给出k最近邻查询以及组反k最近邻查询的形式化定义。 定义3(k最近邻查询[8])给定数据集 P={p1, p2,…,pn}和查询点q,当且仅当一个对象 p∈P满足{pkth∈P|dist(q,p)≤dist(q,pkth) 定义4(组反k最近邻查询[13])给定一组查询点集Q={q1,q2,…,qn}和一个数据点集P={p1,p2,…,pm},当一个对象p∈P在P上的kNN结果包括Q中的任意一个时,p就是GRkNN(Q,P,k)的一个结果,具体定义形式为:GRkNN(Q,P,k)={∃q∈Q,∃p∈P|q∈kNN(p,k,P)}。 3.1查询点集的优化 为了快速地对一组查询点进行组反k最近邻查询,首先需要对这组查询点集进行优化处理。在这一过程中,通过计算获得查询点集Q的质心q(x,y),并用质心q近似地代表查询点集整体。这里,查询点集是一组邻近的查询对象,因此用质心q可以近似地代表查询点集,这样就可以避免搜索区域频繁重叠的情况,从而有效地提高查询效率。 基于以上讨论,进一步给出查询点集的优化算法,如算法1所示。 定理4算法Process_Q(Q,μ,ξ)是正确的、可终止的,其时间复杂度为O(n)。 证明(正确性)Process_Q算法中while语句满足条件时不断地调用两个迭代公式,当dist(q,Q)收敛到最小值ξ时,while循环结束,此时得到的坐标就是所求的质心q的坐标。故该算法能正确地求出查询点集Q的质心q(x,y)。 (可终止性)该算法中只有一个while循环,当不满足条件时,while循环语句可以自行结束,故Process_Q算法是可终止的。 (时间复杂度分析)该算法过程中只有一个while循环,因此该算法的时间复杂度和while循环的时间复杂度是同等级的。设查询点集中的查询点数目为n,则while循环的最坏时间复杂度为O(n)。因此Process_Q算法的时间复杂度为O(n)。□ 3.2约减数据点集 在约减数据点集这一过程中,基于Voronoi图的定理1、2、3给出定理5,根据定理5约减掉不可能成为候选者的数据点,获得初步的候选集。这一过程有效地缩减了数据点的数量,也就是缩小了查询范围,进而提高了查询速度。 定理5q的RkNN只在q的最近邻的前k级邻接生成点中。 证明 由定理3可知,q是Voronoi多边形VP(pi)内任意一点,设q的最近邻为p,则对q的第k+1个最近邻qk+1有qk+1∈AG1(p)⋃AG2(p)⋃…⋃AGk(p)(k为整数,k≥1),即q的第k+1个最近邻在p的前k级邻接生成点中。则显然有qk∈AG1(p)⋃AG2(p)⋃…⋃AGk-1(p),即q的第k个最近邻在 p的前k-1级邻接生成点中。故p的第k级及高于k级的邻接生成点中不可能存在q的kNN。若pj∈AGn(p)(n>k),即pj是p的高于k级的邻接生成点。反过来同理,p是pj的高于k级的邻接生成点。根据定理3,pj的kNN不包括p,也就是q的RkNN不包括pj。综上所述,q的RkNN只在q的最近邻的前k级邻接生成点中。□ 如图1所示,不同类型的虚线连接起来的数据点对象分别是q的1级、2级、3级、4级邻接生成点,设p1、p2、p3、p4分别是q的1级、2级、3级、4级邻接生成点中的一点。当k为3时,由定理3可知,p4的第3个最近邻在p4的前3级邻接生成点中,而p是p4的第4级邻接生成点,因此p4的3NN不包括p。由于q位于VP(p)内,从而q也不是 p4的3NN,即q的反3NN不可能是p4。同理,q的反3NN更不可能是p5,p6,…,pn。 Fig.1 Example of theorem 5图1 基于定理5的示例 本节提出的约减数据点集算法的主要思想为:根据定理5,将q的最近邻前k级邻接生成点放入候选集合Sc中,高于k级的邻接生成点不可能是q的反k最近邻,因此被剪枝。这一过程中首先生成Voronoi图,判断q落在Voronoi图中的具体位置。然后根据q所在Voronoi图中的具体位置分3种情况确定候选集合Sc的范围:第一种情况是q在VP(p)内部,那么Sc就是p的前k级邻接生成点的集合;第二种情况是q在VP(p1)和VP(p2)公共棱上,则Sc就是 p1和p2的前k级邻接生成点集合的并集;第三种情况是q在VP(p1)、VP(p2)、VP(p3)公共顶点上,那么Sc就是p1、p2、p3的前k级邻接生成点集合的并集。基于以上讨论,进一步给出约减数据点集算法,如算法2所示。 定理6算法Reduction_P(Q,P,k)能正确地求出候选集合Sc,是可终止的,其时间复杂度为O(nlgn)。 证明(正确性)该算法首先生成Voronoi图并判断q落在Voronoi图中的具体位置。如果q在VP(p)内部,那么首先获得q的最近邻p,再将p的一级邻接生成点集加入Sc中,最后根据定理5,for循环执行k次将p的前k级邻接生成点集加入Sc中。如果q在VP(p1)和VP(p2)公共边上,那么q的最近邻就变成了{p1,p2},然后同样重复k次for循环将{p1,p2}的前k级邻接生成点集的并集加入Sc中。如果q在VP(p1)、VP(p2)、VP(p3)公共顶点上,那么q的最近邻就变成了{p1,p2,p3},然后根据定理5同样重复k次for循环将{p1,p2,p3}的前k级邻接生成点集的并集加入Sc中,故算法是正确的。 (可终止性)该算法首先生成Voronoi图,因为数据点集中的数据点的个数是一定的,所以生成Voronoi图这一过程是可终止的。然后算法中的3个for循环都是可终止的,故该算法是可终止的。 (时间复杂度分析)该算法生成Voronoi图的时间复杂度为O(nlgn)。for循环的执行过程为k次,3个并列for循环一共执行3k次,k远小于n,故算法2的总时间复杂度是O(nlgn)。□ 3.3剪枝过程 这一过程的主要工作是对候选集Sc进行过滤,剪枝掉大量的非候选者,获取更精确的候选集合。首先利用Voronoi图的邻接特性给出3个高效的剪枝策略,再根据剪枝策略对候选集Sc中的数据点进行判断,若满足条件则被剪枝,Sc中剩下的未被剪枝的数据点构成更精确的候选集。下面以定理形式给出3个剪枝策略及相关证明。 定理7令 p∈AGn(NN(q)),即数据点 p在q的最近邻的第n级邻接生成点中。令p到q的路径上经过的数据点个数不得大于n。将p与查询点q之间的若干路径上的数据点总个数记作sumcount(p,q),如果sumcount(p,q)≥k,则数据点p被剪枝。 证明 设p到查询点q的路径上经过的数据点为pi,当k为1时,显然dist(p,pi)小于dist(p,q),即p的最近邻可能是pi而一定不是q。当k大于1时,如果pi的个数大于或等于k个,即sumcount(p,q)≥k,那么p的kNN可能包括pi中的1到k个,但是一定不包括q。□ 如图2所示,数据点p7在查询点q的最近邻的第3级邻接生成点中。满足p7到q的路径上经过的数据点个数不大于3的路径一共3条,分别是{q,p1,p3, p7}、{q,p2,p4,p7}、{q,p2,p5,p6,p7}。 p7与查询点q之间的3条路径上的数据点总数sumcount(p,q)为6,那么当k等于6时,p7的6NN有可能包括{p1,p2,p3,p4,p5, p6},而一定不包括q。当k小于6时,p7的kNN可能包含{p1,p2,p3,p4,p5,p6}中的1个到k个,而一定不包括q。综上所述,当sumcount(p,q)大于或等于k时,p的kNN查询结果不包括q,即q的RkNN查询结果一定不是p,故数据点p被剪枝。 Fig.2 Example of theorem 7图2 基于定理7的示例 定理8若 p∈AGn(NN(q))被剪枝,那么 p的1级邻接生成点 pi∈Sc满足 pi∈AGn+1(NN(q))条件的也被剪枝。 证明 设p为候选集合中的一点(p∈Sc),pi为p的1级邻接生成点其中之一(pi∈AG1(p)),且pi在候选集中(pi∈Sc)。如果p被剪枝,即sumcount(p,q)≥k,那么sumcount(pi,q)≥k+1。由于sumcount(pi,q)大于k,则根据定理7,p被剪枝。□ 定理9若 p∈Sc且它的1级邻接生成点均被剪枝,则p被剪枝。 证明 设p为候选集合中的一点(p∈Sc),a为p的1级邻接生成点其中之一(a∈AG1(p)),且a是p到q路径上经过的点。若p的1级邻接生成点均被剪枝,显然a也被剪枝,即sumcount(a,q)≥k,那么一定有sumcount(p,q)≥k+1。由于sumcount(p,q)大于k,则根据定理7,p被剪枝。□ 本节提出的剪枝算法的主要思想为:通过定理7、定理8、定理9这3个剪枝策略,获得剪枝后更精确的候选集Sc′。在上一过程的基础上,通过算法1和算法2求得查询点集Q的质心q以及初步的候选集合Sc,接下来根据定理7判断Sc中的数据点p是否应该被剪枝,若p∈AGn(NN(q))被剪枝,再根据定理8,对p的1级邻接生成点pi∈Sc满足pi∈AGn+1(NN(q))条件的也被剪枝。最后根据定理9对Sc中剩下的数据点进行判断,若p∈Sc且它的1级邻接生成点均被剪枝,则p被剪枝。通过对候选集Sc进行过滤,剪掉不可能成为候选者的数据点,获得范围更小的候选集。基于以上讨论,给出剪枝算法如算法3所示。 定理10算法Filter(P,Q,k)能正确地剪枝不可能成为结果的数据点,求出剪枝后更精确的候选集合Sc′,是可终止的,其时间复杂度为O(n),其中n为数据集中数据点的个数。 证明(正确性)该算法的输入是通过算法1获得的查询点集的质心q,以及通过算法2获得的候选集合Sc。算法对候选集合中的每一个数据点p进行判断,求出它到q的若干条路径上经过的数据点总和,若sumcount不小于k,则根据定理7对p进行剪枝。再根据定理8对满足条件的pi剪枝。最后根据定理9对候选集中剩下的数据点进行判断,符合条件的p被剪枝。由于已经证明出定理7、定理8、定理9的正确性,故该算法是正确的。 (可终止性)该算法中有两个嵌套for循环。因为Sc中的候选点数目是有限的,所以第一个for循环可以自行终止。第二个for循环的执行过程为6次,也是可终止的,故该算法是可终止的。 (时间复杂度分析)Filter(P,Q,k)算法中有两个嵌套的for循环。第一个for循环执行的次数取决于Sc中的候选点数目,在最坏情况下Sc中的候选点数目为n(n为数据集中数据点的数目),因此第一个for循环在最坏情况下执行n次。第二个for循环的执行过程为6次,故总共执行6n次。从而该算法的时间复杂度在最坏情况下是O(n)。□ 3.4精炼过程 精炼过程的主要工作是对剪枝后的候选集Sc′进行排错处理,根据反kNN的定义对候选集Sc′中的数据点p进行判断,若满足定义的条件,则p为正确的结果,若不满足条件,则被剪枝。最后得到正确的组反k最近邻的结果集。 本节提出的精炼算法的主要思想为:由反kNN的定义可知,如果数据点p满足dist(q,p)>dist(p,pkth),则p不可能是q的反k最近邻。根据这一条件对候选集中的数据点逐一进行判断。具体过程为:首先通过调用算法1、算法2、算法3分别求得查询点集Q的质心q,初始的候选集Sc以及剪枝后的候选集合Sc′。然后对候选集合Sc′中的每一个数据点p,寻找它的第k个最近邻,记作pkth。如果p到q的距离大于 p到 pkth的距离,则说明q不可能是 p的k最近邻,也就是p不可能是q的反k最近邻查询的结果,将其剪枝,最后得到精确的结果集。由以上论述可得出基于Voronoi图的组反k最近邻查询算法如下。 定理11算法V_GRkNN(Q,P,k)是正确的、可终止的,其时间复杂度为O(nlgn)。 证明(正确性)该算法首先调用的算法1、算法2、算法3均是正确的。然后寻找p的第k个最近邻,若候选集中的点p到q的距离大于p到pkth的距离,则说明p不可能是q的反k最近邻查询的结果,将其剪枝。最后得到的未被剪枝的候选集中的数据点就是组反k最近邻查询的结果,故该算法是正确的。 (可终止性)该算法首先调用的算法1、算法2、算法3均是可终止的。在语句5的for循环中,因为候选集中数据点的个数是有限的,所以for循环是可自行终止的。语句7中的for循环是从1循环到k,其中k是GRkNN查询的k值,是有限的,因此该for循环也是可终止的,故该算法是可终止的。 (时间复杂度分析)该算法执行算法1的时间复杂度为O(n);执行算法2的时间复杂度为O(nlgn);执行算法3在最坏情况下的时间复杂度为O(n);执行嵌套for循环的最坏时间复杂度为O(kn),其中k是组反k最近邻查询的k值,故该算法的时间复杂度为O(nlgn+(k+2)n),化简为O(nlgn)。□ 通过实验对本文算法V_GRkNN进行性能评估。为了验证算法的有效性,将本文提出的基于Voronoi图的V_GRkNN方法分别与文献[13]提出的FCINCH算法以及一种基本算法进行实验比较。把这种基本算法称作GRkNN算法。 GRkNN算法的主要思想为:将现有的针对一个查询对象的RkNN查询算法应用到一组查询对象的情况中,也就是对一组对象中的每个对象成员进行RkNN查询,所有查询结果的并集就是GRkNN查询的结果。具体算法步骤如下: (1)计算一组查询对象中每个查询点的反k最近邻查询结果; (2)求出所有查询结果的并集,得到GRkNN查询的结果。 实验平台配置如下:2.0 GHz CPU,4 GB内存,500 GB硬盘,Windows 7操作系统,用Microsoft Visual Studio 2005实现。本文使用的数据集是Nav Tech公司提供的真实数据集,该数据集用于汽车上GPS设备的导航系统,包括洛杉矶市中心道路系统上的将近79 800个节点对象[20]。n表示数据点集的规模,查询点集Q是在数据点集空间内随机抽出的m个点的集合。本文使用的是Voronoi图的索引结构VTree,VTree索引的每个节点最多包含24个索引项。实验测试的指标为算法的查询时间,并取执行100次查询的平均值。分别测试k值、查询点数量、数据点集大小对算法查询时间的影响以及k值对候选者数量的影响。 Fig.3 Effects of k on query time图3 k值对查询时间的影响 如图3所示,首先分析k值对查询时间的影响。实验采用真实数据集,规模为79 800,查询点的数量为10。图3给出了3个算法的查询时间随着k值变化的对比结果。随着k值的不断变大,3个算法的查询时间均呈上升趋势,其中GRkNN算法的上升趋势显著,V_GRkNN以及FCINCH算法上升趋势比较平缓。由于GRkNN算法需要对每一个查询点计算它的RkNN,这样就造成了搜索区域频繁重叠的情况,从而降低了查询速度。FCINCH算法通过计算查询对象的最小覆盖圆,将圆中的对象作为一个整体来计算该组查询点RkNN的搜索区域,有效地缩小了查询区域,但是时间复杂度略高。而本文的V_GRkNN算法分别对查询点集和数据点集进行了预处理,缩小了查询范围,同时利用Voromoi图的特性进行高效的剪枝和精炼,故算法的时间复杂度比FCINCH算法较低一些。当k为1时,V_GRkNN算法的CPU执行时间比FCINCH略长,因为V_GRkNN在生成Voronoi图过程中需要花费时间,但是随着k的变大,该算法的优势明显。由以上讨论可得出,总体上V_GRkNN算法的查询时间比FCINCH算法略短一些。 图4给出了查询点数量对查询时间的影响。实验设定k值为10,数据点集的规模设置为79 800。从图中可以看出3个算法的查询时间都是随着查询点个数的增多而逐渐增加。其中GRkNN算法的查询时间上升趋势明显,因为需要对每一个查询点计算它的RkNN,当查询点数量成倍数增长时,该算法所用的查询时间也成倍数增长。而FCINCH和V_GRkNN算法的查询时间的上升趋势较为平缓,因为算法中都有对查询点集的处理过程,所以当查询点数量成倍数增长时,对算法的性能影响不大。在优化查询点集阶段V_GRkNN算法的时间复杂度低于FCINCH算法,因此V_GRkNN算法的性能优于FCINCH算法。 Fig.4 Effects ofQon query time图4 查询点数量对查询时间的影响 接下来分析k值对候选者数量的影响,设定实验规模为79 800,查询点数量为20。如图5所示,随着k值从1增加到20,V_GRkNN算法得到的候选者数量最少,说明V_GRkNN算法的剪枝过程更优化。GRkNN算法的性能最低,因为它的候选集是对每一个查询点计算其搜索区域,但是当查询点距离较近时,会产生搜索区域频繁重叠,这样每个查询点的候选集合就会有很多重复。而V_GRkNN算法首先对数据点集进行约减,排除大量的非候选点,然后利用基于Voronoi图的3个剪枝策略对候选集进行过滤,这样便较大程度地减少了候选者的数量。综上所述,V_GRkNN算法在剪枝阶段性能优于另外两种算法。 Fig.5 Effects of k on candidates number图5 k值对候选者数量的影响 Fig.6 Effects of dataset scale on query time图6 数据点集大小对查询时间的影响 图6给出了数据点集规模的变大对算法查询时间的影响。从图中可以看出,随着数据点集规模的变大,3个算法的查询时间都呈上升趋势。GRkNN算法没有数据点集的约减和剪枝过程,因而性能最低。FCINCH算法在计算搜索区域时,因为没有对数据点集进行约减处理,所以随着数据点集的增大,计算过程所用时间变多。而本文的V_GRkNN算法首先对数据点集进行约减处理,利用Voronoi图的特性可以约减掉大量的非候选点,随着数据点集的变大,对算法性能影响不大。因此如图6所示,V_GRkNN算法的上升趋势比较平缓。综上所述,V_GRkNN算法在约减数据点集方面优于其他算法。 本文利用Voronoi图的性质和相应的剪枝规则,提出了处理组反k最近邻查询的方法,解决了针对空间数据库的组反k最近邻查询的问题。GRkNN查询分为4个过程:处理查询点集,约减数据点集,剪枝过程,精炼过程。首先求出查询点集Q的质心q,由于这组查询点的邻近性,用质心q代表整个查询点集;然后根据定理对数据集进行约减得到初步的候选集;再利用剪枝规则对候选集进行过滤;最后通过精炼算法去掉错误的候选者,获得正确的结果集。理论研究和实验表明,所提算法具有较好的性能。未来的研究重点主要集中在障碍空间下的组反k最近邻查询方面。 [1]Roussopoulos N,Kelly S,Vincent F.Nearest neighbor queries[C]//Proceedings of the 1995 ACM SIGMOD International Conference on Management of Data,San Jose,USA, May 22-25,1995.New York:ACM,1995:71-79. [2]Zhang Liping,Zhao Jiqiao,Li Song,et al.Research on methods of construction of Voronoi diagram and nearest neighbor query in constrained regions[J].Computer Science,2014,41(9):220-224. [3]Tao Yulei,Yiu M L,Mamoulis N.Reverse nearest neigh-bor search in metric spaces[J].IEEE Transactions on Knowledge Data Engineering,2006,18(9):1239-1252. [4]Papadias D,Shen Qiongmao,Tao Yufei,et al.Group nearest neighbor queries[C]//Proceedings of the 20th International Conference on Data Engineering,Los Alamitos,USA,Mar 30-Apr 2,2004.Piscataway,USA:IEEE,2004:301-312. [5]Samna N,Eqemen T,Zhang Rui.Incremental evaluation of visible nearest neighbor queries[J].IEEE Transactions on Knowledge Engineering,2010,22(4):665-681. [6]Cao Yunjun,Zheng Baihua,Chen Cencai,et al.Visible reverse k-nearest neighbor query processing in spatial databases[J].IEEE Transactions on Knowledge Engineering, 2009,21(8):1314-1327. [7]Yang Zexue,Hao Zhongxiao.Continuous visible reverse nearest neighbor queries in spatial databases[J].Journal of Southwest Jiaotong University,2012,47(3):451-457. [8]Zhang Ying,Lin Xuemin,Zhu Gaoping,et al.Efficient rank based kNN query processing over uncertain data[C]//Proceedings of the 26th International Conference on Data Engineering,Long Beach,USA,Mar 1-6,2010.Piscataway,USA: IEEE,2010:28-39. [9]Li Song,Zhang Liping,Hao Zhongxiao.Strong neighborhood pair query in dynamic dataset[J].Journal of Computer Research and Development,2015,52(3):749-759. [10]Wang Li,Qin Xiaolin,Shi Changyue.Bichromatic reverse nearest neighbor queries in indoor space[J].Journal of Frontiers of Computer Science and Technology,2015,9(3):310-320. [11]Li Jiajia,Wang Botao,Wang Guoren,et al.A survey of query processing techniques over uncertain mobile objects[J]. Journal of Frontiers of Computer Science and Technology, 2013,7(12):1057-1072. [12]Wu Wei,Yang Fei,Chan Cheeyong,et al.Continuous reverse k-nearest-neighbor monitoring[C]//Proceedings of the 9th International Conference on Mobile Data Management, Beijing,Apr 27-30,2008.Piscataway,USA:IEEE,2008: 132-139. [13]Song Xiaoyu,Yu Chengcheng,Sun Huanliang,et al.GRkNN: group reverse k-nearest-neighbor query in spatial databases [J].Chinese Journal of Computers,2010,33(12):2229-2238. [14]Sun DongPu,Hao Zhongxiao.Group nearest neighbor queries based on Voronoi diagrams[J].Journal of Computer Research and Development,2010,47(7):1244-1251. [15]Li Hongga,Lu Hua,Huang Bo,et al.Two ellipse-based pruning methods for group nearest neighbor queries[C]// Proceedings of the 13th Annual ACM International Workshop on Geographic Information System,Bremen,Germany, Nov 4-5,2005.New York:ACM,2005:192-199. [16]Stanoi I,Agrawal D,Elabbadi A.Reverse nearest neighborqueries for dynamic databases[C]//Special Interest Group on Management of Data Workshop on Research Issues on Data Mining and Knowledge Discovery,Dallas,USA,2000:44-53. [17]Tao Yufei,Papadias D,Lian Xiang.Reverse kNN search in arbitrary dimensionality[C]//Proceedings of the 30th International Conference on Very Large Data Bases,Toronto, Canada,Aug 31-Sep 3,2004.San Fransisco,USA:Morgan Kaufmann Publishers Inc,2004:744-755. [18]Wu Wei,Yang Fei,Chan Cheeyong,et al.FINCH:evaluating reverse k-nearest-neighbor queries on location data[J].Proceedings of the VLDB Endowment,2008,1(1):1056-1067. [19]Hao Zhongxiao.Spatial databases theoretical basis[M].Beijing:Science Press,2013. [20]Kolahdouzan M,Shahabi C.Voronoi-based K nearest neighbor search for spatial network databases[C]//Proceedings of the 30th International Conference on Very Large Data Bases, Toronto,Canada,Aug 31-Sep 3,2004.San Fransisco,USA: Morgan Kaufmann Publishers Inc,2004:840-851. 附中文参考文献: [2]张丽平,赵纪桥,李松,等.Voronoi图的构建与受限区域内的最近邻查询方法研究[J].计算机科学,2014,41(9):220-224. [7]杨泽雪,郝忠孝.空间数据库中连续可视反向最近邻查询[J].西安交通大学学报,2012,47(3):451-457. [9]李松,张丽平,郝忠孝.动态数据集环境下的强邻近对查询[J].计算机研究与发展,2015,52(3):749-759. [10]王丽,秦小麟,施常月.室内双色数据集上的反向最近邻查询[J].计算机科学与探索,2015,9(3):310-320. [11]李佳佳,王波涛,王国仁,等.不确定移动对象的查询处理技术研究综述[J].计算机科学与探索,2013,7(12):1057-1072. [13]宋晓宇,于程程,孙焕良,等.GRkNN:空间数据库中组反k最近邻查询[J].计算机学报,2010,33(12):2229-2238. [14]孙冬璞,郝忠孝.基于Voronoi图的组最近邻查询[J].计算机研究与发展,2010,47(7):1244-1251. [19]郝忠孝.空间数据库理论基础[M].北京:科学出版社,2013. ZHANG Liping was born in 1976.She received the M.S.degree from Harbin University of Science and Technology. Now she is an associate professor at Harbin University of Science and Technology.Her research interests include database theory and application,data mining and data query. 张丽平(1976—),女,辽宁铁岭人,硕士,哈尔滨理工大学副教授、研究生导师,主要研究领域为数据库理论及应用,数据挖掘,数据查询。 LIU Lei was born in 1990.She is an M.S.candidate at Harbin University of Science and Technology.Her research interests include data mining and data query. 刘蕾(1990—),女,黑龙江哈尔滨人,哈尔滨理工大学硕士研究生,主要研究领域为数据挖掘,数据查询。 LI Song was born in 1977.He received the Ph.D.degree from Harbin University of Science and Technology.Now he is an associate professor at Harbin University of Science and Technology.His research interests include database theory and application,data mining and data query. 李松(1977—),男,江苏沛县人,博士,哈尔滨理工大学副教授、研究生导师,主要研究领域为数据库理论及应用,数据挖掘,数据查询。 YU Jiaxi was born in 1991.She is an M.S.candidate at Harbin University of Science and Technology.Her research interests include data mining and data query. 于嘉希(1991—),女,黑龙江哈尔滨人,哈尔滨理工大学硕士研究生,主要研究领域为数据挖掘,数据查询。 Group Reverse k Nearest Neighbor Query Based on Voronoi Diagram in Spatial Databasesƽ ZHANG Liping+,LIU Lei,LI Song,YU Jiaxi E-mail:zhanglptg@163.com To overcome the limitation of query objects in group reverse k nearest neighbor(GRkNN)query,this paper proposes the group reverse k nearest neighbor query method based on Voronoi diagram(V_GRkNN).The proposed method finds data points that take any point in the query objects set as one of their k nearest neighbors.In the practical application,V_GRkNN query can be used to evaluate the influence of a group of query objects.Firstly,the query points set Q is optimized in order to reduce the effect of the query points number on query efficiency,the data points set P is pruned to reduce the searching ranges.And then according to the pruning strategies based on Voronoi diagram,the candidate set is filtered.Finally,a refinement process is used to get the query Ƴ s final results.The V_GRkNN method greatly improves the query speed and efficiency.Theoretical research and experiments show that the efficiency of the proposed V_GRkNN method obviously outperforms other algorithms. Voronoi diagram;reverse k nearest neighbor;group reverse k nearest neighbor;index structure 2015-08,Accepted 2015-10. 10.3778/j.issn.1673-9418.1508004 A TP311.13 *The National Natural Science Foundation of China under Grant No.61370084(国家自然科学基金);the Natural Science Foundation of Heilongjiang Province under Grant No.F201302(黑龙江省自然科学基金);the Science and Technology Research Project of Heilongjiang Education Department under Grant Nos.12541128,12531z004(黑龙江省教育厅科学技术研究项目). CNKI网络优先出版:2015-10-20,http://www.cnki.net/kcms/detail/11.5602.TP.20151020.1041.008.html ZHANG Liping,LIU Lei,LI Song,et al.Group reverse k nearest neighbor query based on Voronoi diagram in spatial databases.Journal of Frontiers of Computer Science and Technology,2016,10(10):1365-1375.3 基于Voronoi图的组反k最近邻查询
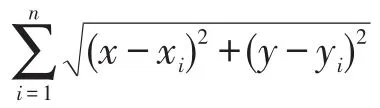
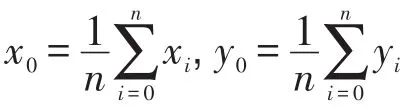






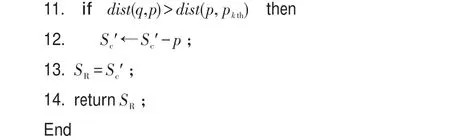
4 实验与分析
5 结束语




College of Computer Science and Technology,Harbin University of Science and Technology,Harbin 150080,China

