基于MBF参数模型的安全完整性等级定量评估
马 奔, 孙自强(华东理工大学化工过程先进控制和优化技术教育部重点实验室,上海 200237)
基于MBF参数模型的安全完整性等级定量评估
马 奔, 孙自强
(华东理工大学化工过程先进控制和优化技术教育部重点实验室,上海 200237)
介绍了安全完整性等级验证的相关内容,并对系统发生危险失效因素进行分析;在引入MBF(Multiple Beta Factor)参数模型的基础上,定量计算系统发生共因失效的概率,并研究系统发生独立危险失效的概率及其影响;最后给出应用实例进行验证。结果表明:本文方法不仅更接近工业生产中安全仪表系统冗余结构的实际情况,也大大简化了计算,弥补了马尔可夫模型法分析计算过程复杂的缺陷。
安全完整性等级;MBF参数模型;马尔可夫模型;共因失效
随着中国工业化特别是化工工业进程不断加快,重大的生产安全事故频繁发生。如何确保化工生产过程的运行更加稳定、可靠、安全成为大家研究的重点。在控制系统中,安全保护设备和控制设备一般是分离的。控制设备被称为基本过程控制系统(Basic Process Control System,BPCS),而保护设备则被称为安全仪表系统(Safety Instrument System,SIS)。
SIS是安全相关系统(Safety-Related System,SRS)的一类[1],是保障生产安全的重要措施。安全仪表系统可以对工业过程一些重要的工艺参数进行密切实时监测,避免使生产过程持续处于具有安全风险的环境。为了更好地对安全仪表系统的运行水平及减少风险的能力进行评估,一些安全相关标准如IEC61508和ANSI/ISA S84.01提出了一个重要概念——安全完整性等级(Safety Integrity
Levels,SIL)。在定量计算SIL等级的方法中,如何运用马尔可夫模型对系统进行可靠性分析一直是研究的热点;Knegtering等[2]首先提出微马尔可夫模型法计算失效率,但其仅在概念上进行了阐述;Zhang等[3]对系统的可靠性框图进行研究,在其基础上建立微马尔可夫模型,但他们仅对几种典型的冗余结构进行了分析,而且模型结构太过简单,没有考虑共因失效的影响。本文采用基于MBF (Multiple Beta Factor)的共因失效参数模型来简化马尔可夫模型的计算,并综合考虑共因和独立失效对系统的影响,最后给出实例进行验证,结果表明,本文方法可以很好地弥补现有计算方法的缺点。
1 安全完整性水平的验证
安全完整性水平是安全仪表系统的核心,也是设计安全系统的重要依据。在安全系统整体生命周期的设计安装、检验评估、维护修理等阶段都是围绕其安全完整性水平进行的[4]。
系统的安全完整性水平主要与系统失效相关。系统失效主要是由制造过程、文档错误、软件问题等系统性故障所引发的失效。由于系统故障的影响与引入它的生命周期阶段有关,且为避免系统失效的各种单一措施的有效性都与应用有关,故只能用定性的方法分析系统失效。
硬件的安全完整性水平主要与随机硬件失效相关,其SIL等级可以通过定量分析来确定。确定一个系统的硬件安全完整性等级通常需要综合考虑随机失效和结构约束两方面内容,以避免出现过于乐观的失效率数据,从而在不恰当的结构设计情况下得到较高的安全完整性等级。其中,随机失效的安全完整性可以通过计算一个重要的指标来进行评估,即平均需求失效概率(Probability of Failure on Demand,PFD),它是安全仪表系统在整个安全生命周期内发生失效的平均概率。IEC 61508定义了4种安全完整性等级如表1所示。

表1 IEC61508安全完整性等级Table 1 Safety integrity levels of IEC61508
硬件安全完整性的安全功能所能声明的最高安全完整性等级受限于硬件故障裕度(HFT)和执行该安全功能的子系统的安全失效分数(SFF)。其中:λS为系统安全失效概率;λDD为可被诊断功能诊断到的危险失效概率;λD为系统危险失效概率。

硬件故障裕度与系统或部件的结构有关,若用数值K表示,则意味着发生K+1个故障会导致系统安全相关功能失效。对于一个具有Moo N结构的系统,需要其中的M个独立通道来完成其安全功能,在不考虑如诊断等其他可能控制故障影响的措施时,可得K=N-M[5]。
对于TYPE B的子系统,其结构约束条件如表2所示。

表2 硬件安全完整性结构约束Table 2 Integrity safety constraints of hardware structure
2 系统危险失效影响因素分析
2.1概述
IEC 61508对危险失效定义为使安全相关系统处于潜在的危险或丧失功能状态的失效。在计算平均需求失效概率时,我们仅考虑引起系统危险失效的概率。本文将从诊断、共因、冗余结构等方面对安全仪表系统的危险失效进行定性分析。
2.2诊断和修复
在冗余和非冗余结构中,系统检测部件故障的能力即在线诊断对于安全仪表系统的可靠性与安全性具有重要影响。当增加诊断时,不仅可以减少系统在危险模式下的运行时间,减少降级模式(不能完全执行正常功能)下的时间,还可直接干预系统的运行,从而改善其安全性与可用性。其中,一个重要的术语“诊断覆盖率”是指能够诊断出所发生失效的概率。根据不同的失效模式,将其区分为安全失效诊断覆盖率(CS)和危险失效诊断覆盖率
(CD)。衡量系统的诊断覆盖率可以使用失效模式、影响和诊断分析(FMEDA)进行评估。
根据诊断覆盖率危险失效分为检测到的危险失效和未检测到的危险失效。检测到的危险失效可以通过在线诊断系统检测维修;未检测到的危险失效只能在定期的周期性维护测试时进行维修。定义在线维修率为μ0,周期性检查的维修率为μP,计算公式如下:
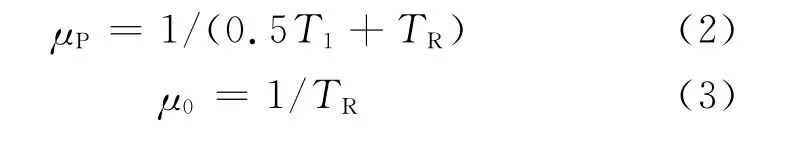
其中:TR是平均修理时间;T1是周期性检查时间。
在系统进入安全失效时,定义一次无故障停车后设备重启时间为SD(Shut Down),检测到的安全失效修复率为μSD,则有

2.3共因失效
安全仪表系统采用冗余结构时,通常会发生共因失效。在对系统失效率进行定量分析时,经常采用β模型对共因失效进行建模,β因子将失效分为共因失效与普通失效两种。由于共因失效会严重降低系统的安全性与可靠性,所以在进行安全仪表系统的设计时,一定要找出与共因失效相关的失效源,并采取一定措施消除其影响。
2.4冗余表决组
通常,组成安全仪表系统的传感器子系统、逻辑控制器子系统和最终元件子系统都会采用多个设备组成Moo N的冗余表决结构,不同的冗余结构具有不同的特点,如1oo1结构即常规的单通道结构,其安全性与可用性都较低;对于双通道结构,1oo2表决结构适用于安全性要求较高的情况,而2oo2结构其安全性较低但具有很高的可用性;1oo3结构具有很好的安全性与可用性,但其成本也较高。
3 系统危险失效率的定量计算
3.1概述
目前,有许多方法计算一个具有Moo N结构系统的PFD值,其中定量计算的方法主要有可靠性框图法、故障树分析法、马尔可夫模型法等。马尔可夫模型法是根据系统过程状态的转移建立马尔可夫模型。由于马尔可夫模型涵盖了多种可靠性指标,具有很好的实时性,所以在可靠性工程中具有广泛的应用。
3.2常用表决结构的马尔可夫模型
对马尔可夫模型进行分析计算时往往考虑的共因失效是基于单β因子,假设系统的N个通道具有完整的对称性,且所有通道具有相同的常数失效率。本文以1oo1单通道结构为例进行分析,这种结构包括一个单通道,若发生任何一种危险失效(包括检测到的和未检测到的)则系统就会发生危险失效。1oo1结构的马尔可夫模型如图1所示。
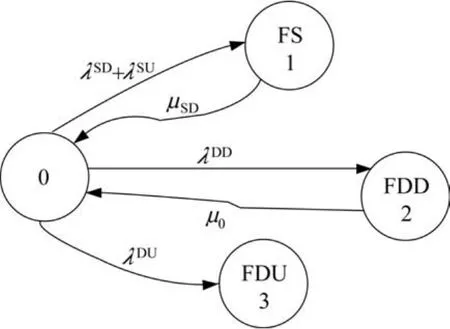
图11 oo1结构马尔可夫模型Fig.1 Markov model for 1oo1 structure
模型中状态0代表正常;状态1表示安全失效状态;状态2表示检测到的危险失效状态,并可以维修;状态3表示未检测到的危险失效状态。1oo1系统的状态转移矩阵Q为

在初始状态,所有设备正常工作,即初始状态向量S0=[1 0 0 0],由于模型中状态2、3为危险失效状态,所以其危险失效向量为VD=[0 0 1 1]T。假设测试时间间隔为T1,则1oo1结构的危险失效率为
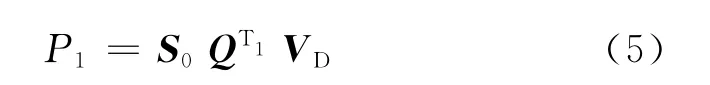
由以上分析可以知道,尽管马尔可夫模型在描述系统不同状态的动态转移过程时具有很大的灵活性,但随着状态的增加,其转移矩阵的维数将急剧增加,造成分析过程复杂及计算空间爆炸的问题,所以我们可以考虑基于MBF(Multiple Beta Factor)的共因失效参数模型来简化马尔可夫的计算过程。
3.3考虑MBF的共因失效模型计算
共因失效往往是系统级的失效或者是随机硬件失效,在IEC 61508中对共因失效模型计算其需求失效率时仅仅考虑单β因子,然而,对于不同的冗余结构,单β因子模型并不能很好地描述共因失效,所以引入更具有一般性的MBF参数模型以区分β因子在不同冗余结构中的影响。
在MBF参数模型中,假设如下:
(1)系统的各种冗余结构由完全相同的通道配置而成,一个Moo N结构的每个通道都可以看作是一个1oo1结构。
(2)系统的N个通道具有完整的对称性,每个通道都具有相同的恒定失效率且各通道相互独立。
因此,对于一个具有Moo N结构的系统,由于共因失效所引起的系统失效率(PC)为

其中:CMooN为不同系统结构共因失效配置影响因子;β为单β因子(仅适用于2个通道);P1为单通道失效率。根据上述定义,当系统通道数N为2时,β 在MBF模型中与IEC 61508标准中意义相同,所以C1oo2=1。
为了确定不同系统结构的共因失效率,必须对CMooN进行估计。定义以下参数:
gj,n:在具有n个通道的系统中,有j个特定的通道发生失效的概率。
fj,n:在具有n个通道的系统中,有j个通道发生共因失效的概率。故有
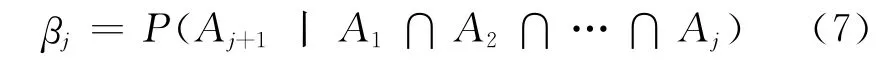
式(7)中:Aj表示通道j发生共因失效,根据定义有β=β1。在具有n个通道的系统中,有j个特定的通道发生失效的概率为
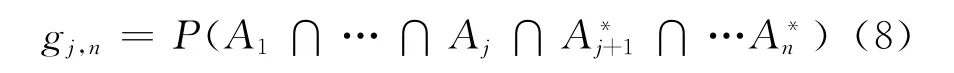
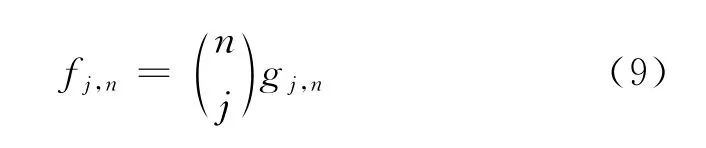
对于一个具有koon结构的系统,则至少有nk+1个通道发生共因失效才会引起系统失效,所以系统失效的概率如下:

因为Ckoon与β、P1相互独立,由式(10)得[6]
单项运动本身所具有的魅力足以吸引大众的参与,形形色色的项目汇聚在一起时反而会显得杂乱无章,凸显不出小镇的特色。聚焦于自身优势,把一个项目做到极致,让大众在体验中真正感受到这项运动的韵味,培养运动锻炼的兴趣,这便是体育特色小镇建造宗旨的关键所在。
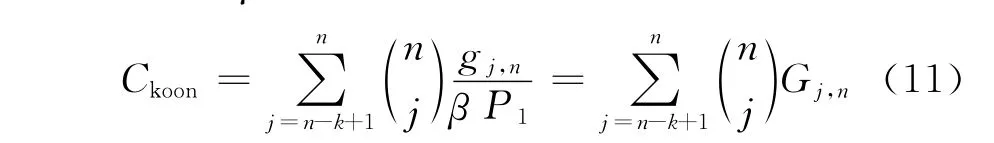
且有k=1,2,…,n-1。根据文献[6-7]可知道,
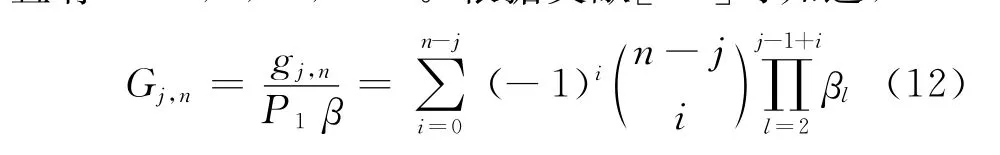
其中j=2,3,…,n,且Gj,n满足以下关系式:

式中:j=n-1,n-2,…,1。根据专家对系统失效多样性分布的实验研究,令β2=0.3,βp=0.5,p≥3,经过计算,得到不同系统结构CMooN的值如表3[8]所示。
因此,在计算一个Moo N结构系统由于共因失效所引起的系统失效率时,首先对其中的一个通道建立1oo1的马尔可夫模型,计算其单通道的危险失效率P1,然后对应表3查出系统结构的配置影响因子CMooN,再根据式(6)计算其共因失效率。由此,避免了对大型冗余系统建立马尔可夫模型,大大简化了计算。
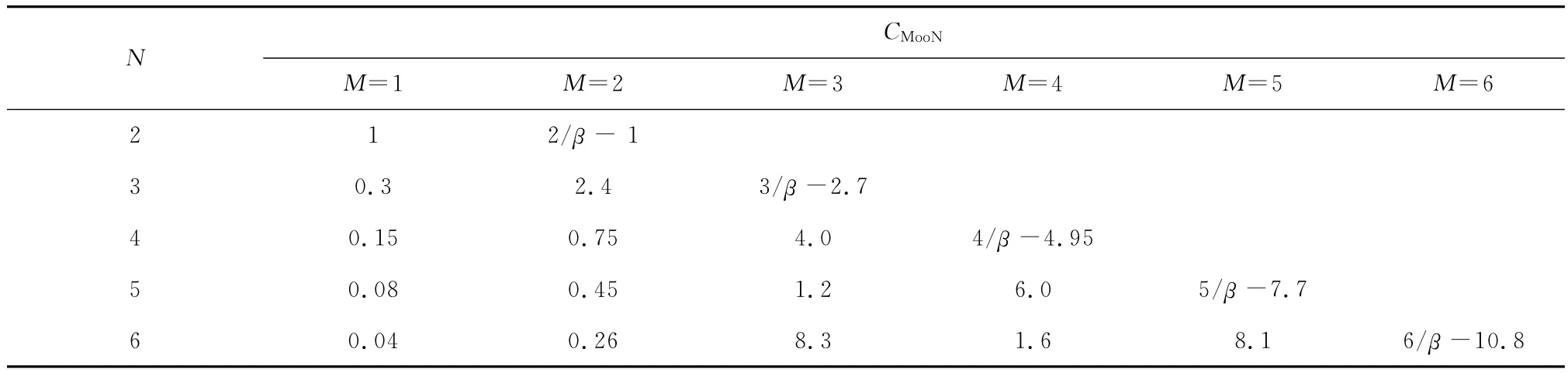
表3 不同系统结构的CMooN值Table 3 Values of CMooNfor different system structures
3.4独立危险失效率的计算
除了由于共因引起的系统失效,我们还必须考虑设备同时发生独立危险失效所引起的系统失效概率。对于Moo N结构,至少有N-M+1个通道同时发生独立危险失效时,则系统失效。其失效率
(P I)为
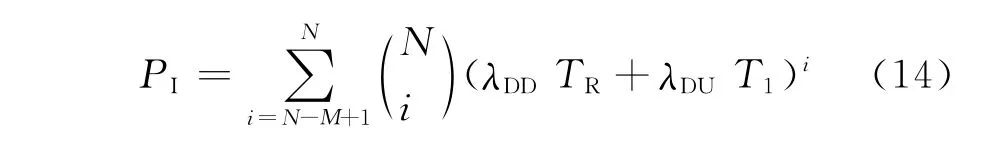
由于当i=N-M+2,N-M+3,…,N时,系统发生独立失效的概率相对于i=N-M+1时已经很小,且TR<<T1,所以公式简化为
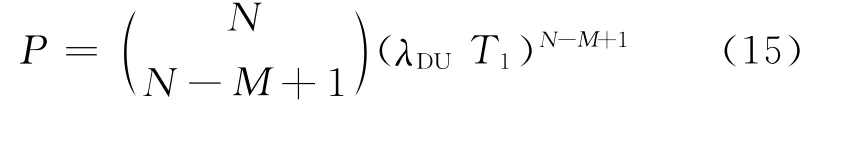

综上所述可以求得系统发生危险失效的概率为

深入研究发现,当N-M+1足够大时,N-M+1个通道同时发生独立危险失效的概率很小。例如,要使SIS满足最高完整性等级SIL4,则其PFD值最高为10-4,若给定其他参数,通过迭代计算当N-M+1≥4,即硬件故障裕度HFT≥3[9]时,N-M+1个通道同时发生独立危险失效的概率远小于设备所要求的最高失效率10-4,此时可忽略独立危险失效的影响。
4 不同方法之间的比较
4.1计算效率对比
为了研究传统马尔可夫建模方法计算的效率,必须确定MooN结构模型中所有状态个数,即其状态转移矩阵的大小。定义状态向量F=[nSD,nSU,nDD,nDU],其中nSD与nSU分别代表检测到的和未检测到的安全失效的个数,nDD与nDU分别代表检测到的和未检测到的危险失效的个数,定义d为系统中失效的总数量,令nS=nSD+nSU,由此可知当nS≥M时,系统为安全失效状态;当F=[0,0,0,0],即d= 0时为初始状态。对文献[10]中自动创建马尔可夫模型的方法进一步研究,推导出如下公式:
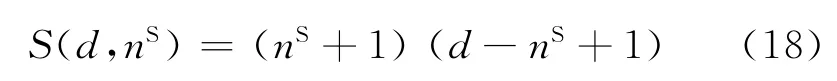
其中:d=1,2,3…,N;nS=0,1,2…,M-1,且nS≤d;S(d,nS)仅由d与nS决定,定义为Moo N结构马尔可夫状态转移过程中的中间状态和发生危险失效状态个数的和。系统总状态个数为S(d,nS)与初始状态、安全失效状态个数的和即S(d,nS)+2。以1oo2结构为例求其包含状态的总数量:S(1,0)=2;S(2,0)=3,故其状态总个数为S(1,0)+S(2,0)+2=7,即1oo2结构的系统具有7×7的状态转移矩阵。因此得到MooN结构的状态总个数即其状态转移矩阵大小如表4所示。
由于一个N×N的矩阵相乘一次,需要2N3次浮点运算(FLOPS-floating point operations)完成计算,所以对于一个2oo3结构的系统,由表4可知其状态转移矩阵大小为23×23,所以其相乘一次需要24 334 FLOPS,若采用MBF模型的方法,所有结构只需对1oo1结构的4×4转移矩阵进行计算,相乘一次仅需要128 FLOPS。由此可知,采用本文方法计算效率会显著提高,若结构更加复杂的话,其效果将会更加明显。
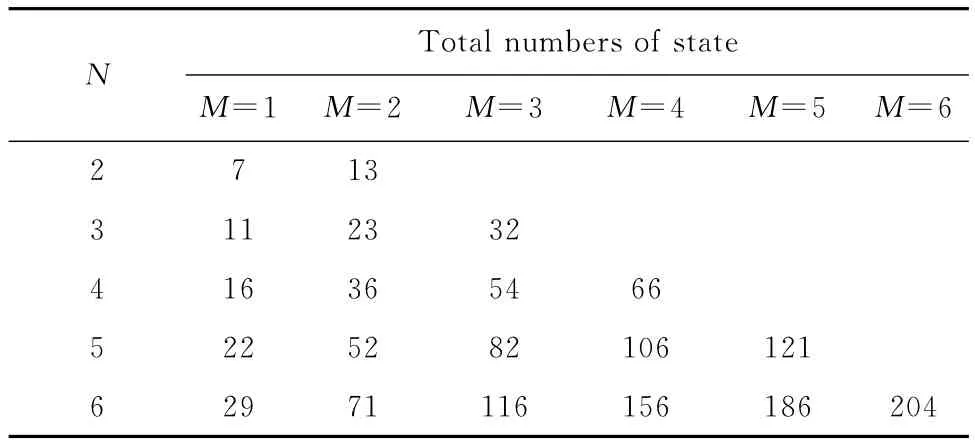
表4 不同Moo N结构状态个数Table 4 Number of state for different Moo N structure
4.2计算结果比较
假设β=0.03,λSD=9.996×10-6,λSU=9.8× 10-8,λDD=5.996×10-6,λDU=1.12×10-7,平均修复时间TR为8 h,周期性检查时间T1为8 760 h,一次无故障停车后装置重启时间SD(Shut Down)为24 h,则有μ0=1/TR=0.125;μSD=1/SD= 0.041 7。
根据以上数据,利用MBF模型求得的PFD值与普通马尔可夫方法所求的值对比结果如表5所示。在用普通方法计算PFD值时,由于N≥4系统结构的马尔可夫模型非常复杂,采用故障树模型近似计算。
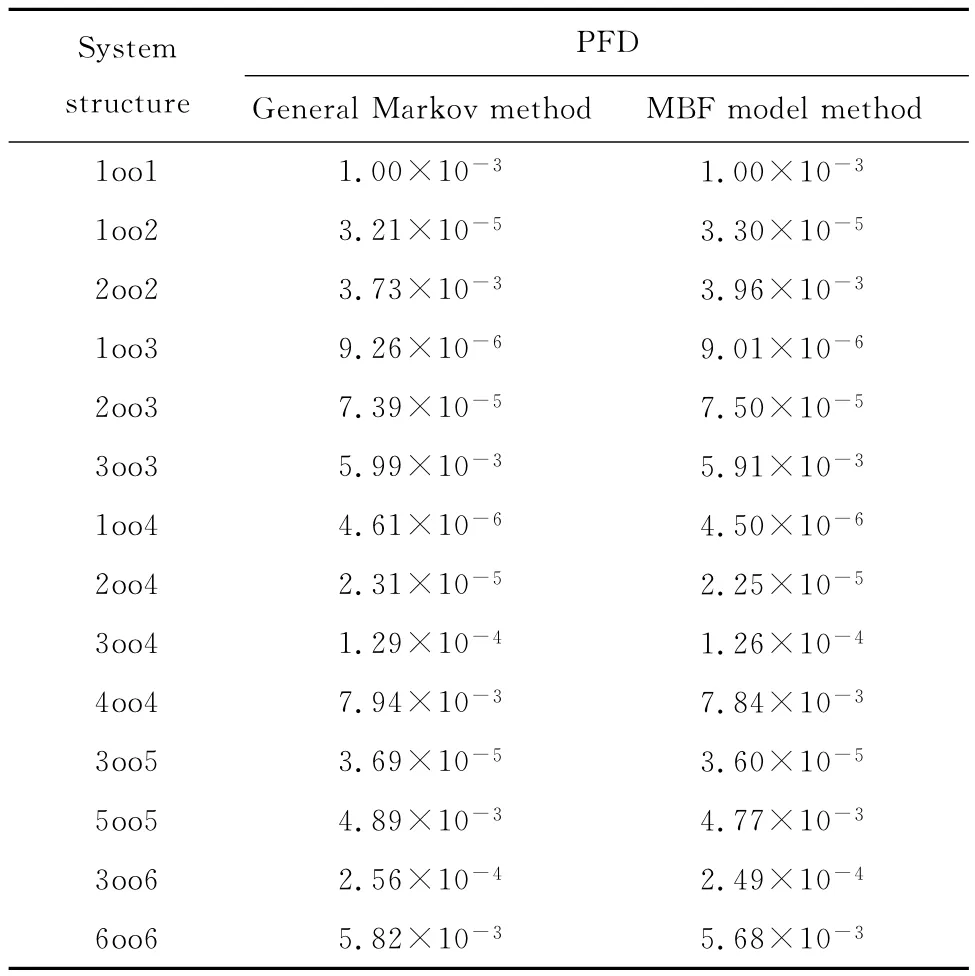
表5 PFD计算结果比较Table 5 Comparison of PFD calculation results
由表5可知,两种方法的结果具有很好的一致性,但本文方法具有很高的计算效率,且省略了复杂的马尔可夫建模过程,使计算更加简便。
5 实例验证
在工业生产中,压力保护系统是安全仪表系统中最典型的例子。图2所示为一套化工石油生产中的高完整性压力保护系统(High Integrity Pressure Protection System,HIPPS)。通过隔断上游部分产生的过压源,降低了下游设备的压力等级,减少了系统由于超压带来的危险性。
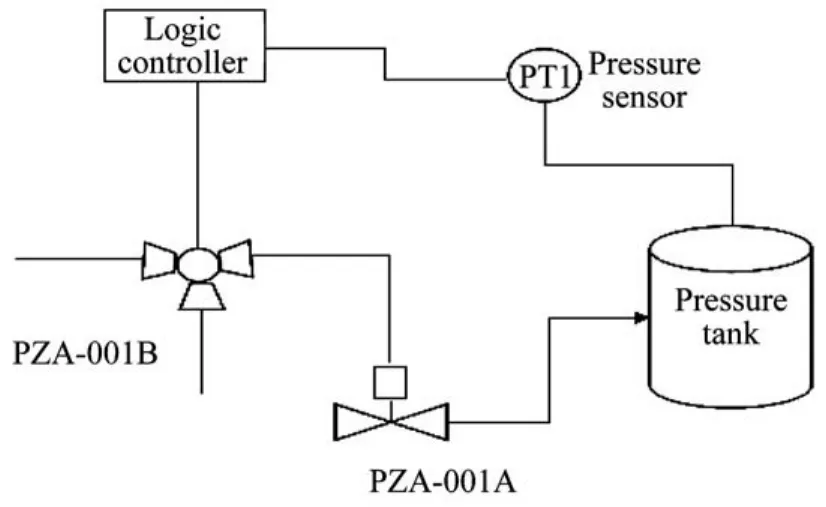
图2 高完整性压力保护系统示意图Fig.2 HIPPS schematic diagram
图2所示的HIPPS安全仪表系统由均为1oo1冗余结构的压力传感器子系统、逻辑控制器子系统、执行器(阀门)子系统组成。首先,压力传感器检测储罐内的压力,若压力超过给定限值,则触发高保护设定点,将信号传递至逻辑控制器,并由逻辑控制器发送关断信号控制阀门PZA-001B、PZA-001A断开,从而保护压力储罐。根据生产安全性要求,我们要设计满足安全完整性等级为SIL2的压力保护系统,该压力保护系统相关设备失效率数据[11]如表6所示,且TR=8 h,T1=8 760 h,SD=24 h。
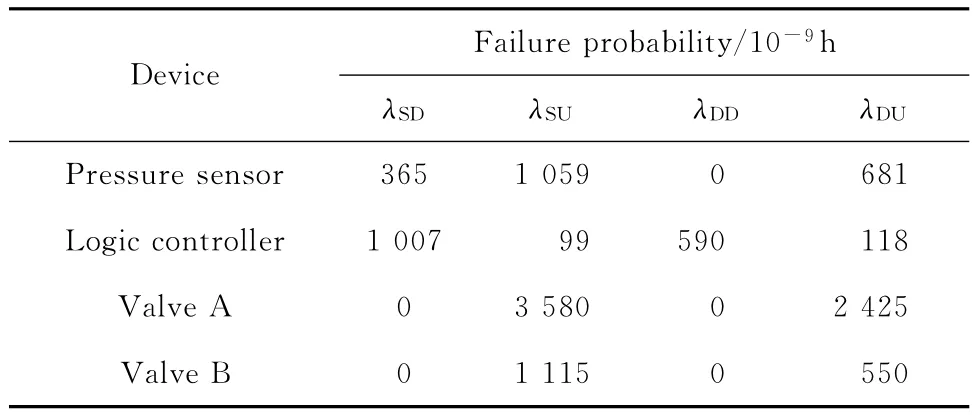
表6 HIPPS设备失效率数据Table 6 Equipment failure data of HIPPS
由于该系统的各子系统均为1oo1冗余结构,分别对其建立马尔可夫模型,并将上述失效率数据分别代入状态转移矩阵Q得到Q1、Q2、Q3,根据式(5)得
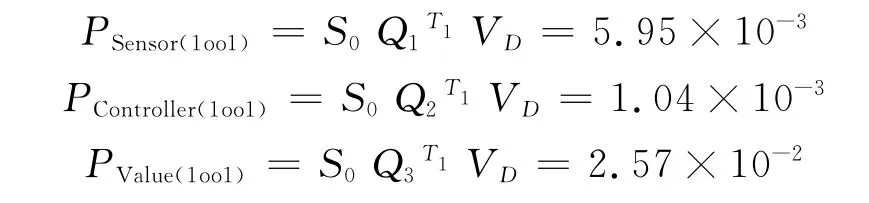
由此得该压力保护系统总平均危险失效率为

由此可得该压力保护系统并不满足所要求的安全完整性等级,需要对各子系统进行冗余结构配置。若将传感器子系统配置成2oo3结构,逻辑控制器和阀门子系统配置成1oo2结构,令β=0.05,根据式(17)分别计算各子系统的危险失效率。
(1)传感器子系统
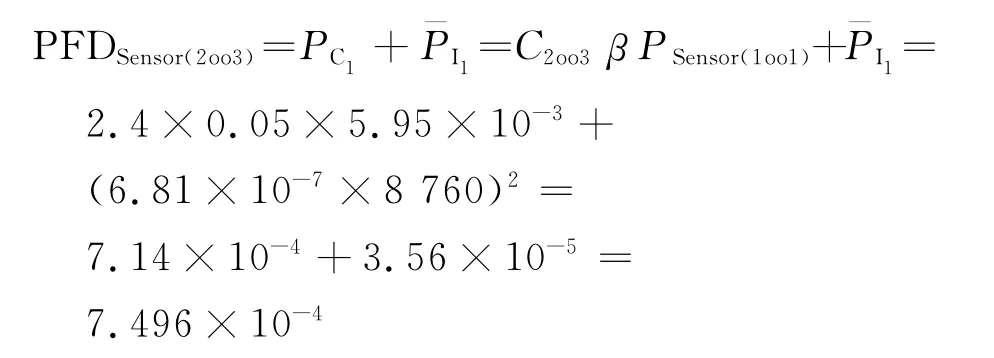
(2)控制器子系统
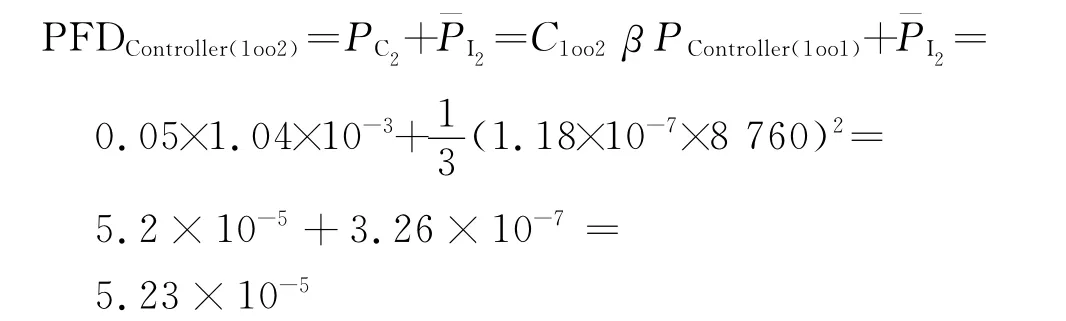
(3)阀门子系统
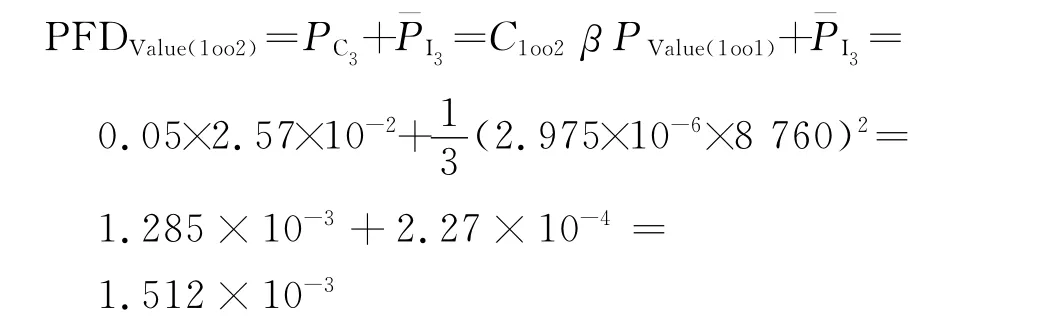
(4)系统整体平均危险失效率
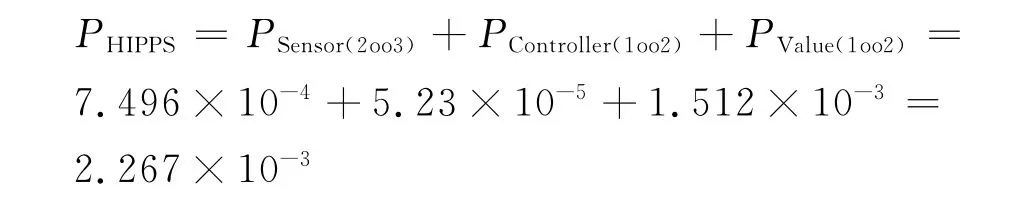
由上可知,该压力保护系统满足安全完整性等级为SIL2的要求。
若采用普通马尔可夫建模,通过已有模型计算得该压力保护系统危险失效率为2.966×10-3,与本文计算结果具有很好的一致性。在用常规的马尔可夫建模法设计系统的冗余结构时,必须对每一个子系统建立马尔可夫模型,并对模型逐一分析计算,与此相比,本文方法可以很方便地计算每个子系统的失效率,并根据失效率快捷地设计满足所需安全完整性等级的仪表系统。
6 结束语
近年来,由于化工行业事故频发,如何设计并利用安全仪表系统来保证生产过程的平稳安全运行已经成为研究热点,而安全完整性等级是安全仪表系统的核心,不管是在设计安全系统之初或是在设计完成试运行之后,其SIL等级都是对其系统功能安全评估的重要依据。本文引入更具有一般性的MBF参数以区分β因子在不同冗余结构中的影响,根据结构配置因子计算其共因失效率,并对独立危险失效进行研究。本文方法不仅更接近工业生产的实际情况,避免了对安全仪表系统功能安全水平的估计过于乐观或保守,也大大简化了计算,使安全仪表系统结构的配置更加方便。
[1] 靳江红,吴宗之,赵寿堂,等.安全仪表系统的功能安全国内外发展综述[J].化工自动化及仪表,2010,37(5):1-5.
[2] KNEGTERING B,BROMBACHER A.Application of micro Markov models for quantitative safety assessment to determine safety integrity levels as defined by the IEC 61508 standard for functional safety[J].Reliability Engineering and System Safety,1999,66(2):171-175.
[3] ZHANG Tieling,LONG Wei,SATO Y.Availability of systems with self-diagnostic components-applying Markov model to IEC 61508-6[J].Reliability Engineering and System Safety,2003,80(2):133-141.
[4] 郭海涛,阳宪惠.安全系统的安全完整性水平及其选择[J].化工自动化及仪表,2006,33(2):71-75.
[5] 杨栩楠.功能安全与微控制器自诊断技术的研究[D].北京:北京交通大学,2010.
[6] HOKSTAD P,MARIA A,TOMIS P.Estimation of common cause factors from systems with different number of channels [J].IEEE Transactions on Reliability,2006,55(1):18-25.
[7] HOKSTAD P,CORNELIUSSEN K.Loss of safety assessment and the IEC61508 standard[J].Reliability Engineering and System Safety,2004,83(1):111-120.
[8] SHU Yidan,ZHAO Jinsong.A simplified Markov-based approach for safety integrity level verification[J].Journal of Loss Prevention in the Process Industries,2014,29:262-266.
[9] 李红,赵建平.故障树法在大型冗余结构失效率计算中的应用[J].仪表技术与传感器,2012(12):86-88.
[10] GUO Haitao,YANG Xianhui.Automatic creation of Markov models for reliability assessment of safety instrumented systems[J].Reliability Engineering and System Safety,2008,93(6),807-815.
[11] 张亨.化工装置安全仪表系统功能安全评估体系的研究与应用[D].上海:华东理工大学,2013.
Quantitative Assessment of Safety Integrity Levels Based on MBF Model
MA Ben, SUN Zi-qiang
(Key Laboratory of Advanced Chemical Process Control and Optimization Technology,Ministry of Education,East China University of Science and Technology,Shanghai 200237,China)
This paper introduces the safety integrity level verification and analyzes the dangerous failure factors of the considered system.By using MBF parameter model,this paper quantitatively calculates the probability of common cause failure of the system.Moreover,the impact of independent failure probability for the safety instrument system is analyzed.Finally,the application example shows that the proposed method is not only closer to the actual redundant structure of safety instrument system in the industrial production,but also greatly simplifies the calculation and deals with the shortcoming of Markov model with complicated calculating procedure.
safety integrity levels;MBF parameter model;Markov model;common cause failure
TP277
A
1006-3080(2016)01-0097-07 DOI:10.14135/j.cnki.1006-3080.2016.01.016
2015-04-21
上海市重点学科建设基金(B504)
马 奔(1992-),男,硕士生,研究方向为仪表功能安全技术。E-mail:970422373@qq.com
孙自强,E-mail:sunziqiang@ecust.edu.cn

