基于双调制随机共振的涡街信号检测方法*
丁君鸿,黄咏梅,林 敏
(中国计量学院计量测试工程学院,杭州310018)
基于双调制随机共振的涡街信号检测方法*
丁君鸿,黄咏梅*,林敏
(中国计量学院计量测试工程学院,杭州310018)
研究一种用于涡街流量计涡街频率测量的随机共振信号处理方法。探讨了信号与双稳系统的阈值和克莱默斯逃逸率之间的关系,通过外加幅值和频率可调的信号进行双重调制,实现信号与双稳系统的匹配,数值仿真表明该匹配方式是可行和有效的。针对涡街信号,提出基于标准差的调制参数选取方法,该方法利用涡街信号特征,通过信号标准差估计管道内流速,缩小了调制参数的选取范围,提高了信号与双稳系统匹配的效率。实验结果表明,利用标准差选取调制参数对涡街信号进行调制,可以有效地使涡街信号,特别是弱涡街信号产生随机共振,进而检测到涡街频率,实现流量测量。
信号处理;随机共振;信号调制;涡街流量计;
EEACC:7210;7310Gdoi:10.3969/j.issn.1004-1699.2016.05.017
涡街流量计是一种振动式流量计,理想情况下,传感器输出信号近似于余弦,其频率与流速成正比,然而工业现场的各种振动,使涡街信号混入了噪声,特别是在小流量测量时,涡街信号弱,容易被噪声淹没,导致测量受限[1-2]。国内外学者对涡街信号处理方法做了许多研究,如经典频谱分析法、小波变换法、自适应滤波法等[3-5]。这些方法多通过信号与噪声的特性差异削弱噪声提取信号,在处理过程中难免会损害有用信号,具有一定局限性。
随机共振是一种非线性处理方法,有别于目前线性处理方法,在非线性双稳系统、信号与噪声三者的共同作用下,利用噪声的积极作用和非线性系统对外界周期信号的灵敏性,可以将噪声能量用于增强微弱信号[6-8]。对于涡街信号容易受现场噪声干扰的情况,采用随机共振方法可以改善测量精度,拓展测量下限。但随机共振的产生是有条件的,信号的频率及幅值与系统匹配,才能产生随机共振[9-10]。涡街信号的频率及幅值的变化范围较大,如何人为有效地使信号与系统之间实现匹配,是产生随机共振的关键。本文提出通过频率及幅值可调的信号对涡街信号进行双重调制,并针对涡街信号,提出利用信号标准差选取调制参数的方法,进而使涡街信号产生共振,实现频率检测。
1 调制随机共振机理
1.1随机共振原理
非线性双稳系统的动力学方程可用Langevin方程表示,如式(1)所示:
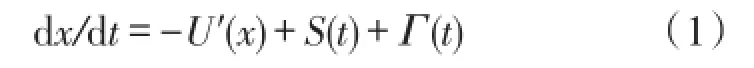
式中S(t)=Acos(2πft)为周期信号,Г(t)是强度为D的高斯白噪声,双稳系统的势函数如式(2)所示:
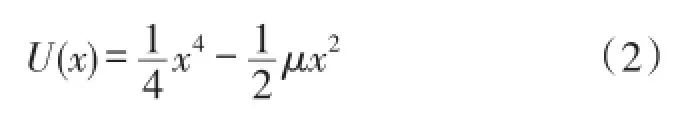
式中,μ为系统参数。
双稳系统具有两个势阱和一个势垒,势阱底部位于x1,2=±μ处,势垒位于x=0处,势垒高度ΔU= μ2/4,At=34μ3/27为系统维持双稳态的阈值,当输入信号幅值A>At时,输出将在x1=μ与x2=-μ两个势阱之间周期变化,当A<At时,系统输出将在单一势阱内小范围变化,此时若系统在信号和噪声共同作用下,输出可能越过势垒在两势阱间周期变化,这一现象称为随机共振[11]。
双稳系统与信号,噪声共同作用产生随机共振是有条件的,根据克莱默斯逃逸率理论,系统中的布朗粒子在两个势阱间跃迁的速率如式(3)所示
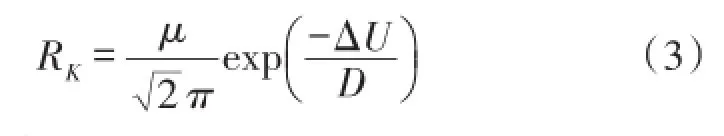
只有输入信号频率f小于RK时,粒子的跃迁速率才能够跟上信号频率产生共振[12-13]。在频率一定的条件下,良好的共振状态还需要信号幅值A与系统阈值At之间满足一定匹配关系,根据输出共振状态不同可以分为欠共振,过共振及共振。A>At时,输出能够直接在势阱间变化,但噪声也直接作用到输出端,易造成过共振。A<<At时,由于信号能量弱,输出无法越过势垒造成欠共振,两种情况都不能有效地检测到信号频率,只有信号幅值A<At,同时与At相差不大的情况下,信号、噪声及双稳系统才能更好地产生协同作用,产生随机共振。
因此人为有效地实现涡街信号与系统之间匹配,产生随机共振是涡街频率检测的关键。
1.2双调制随机共振原理
涡街信号由漩涡产生的周期信号及现场的噪声叠加而成,其中周期信号幅值和频率随流量大小而变化,且变化范围较大,其频率和幅值不能完全符合系统产生随机共振的要求,直接将涡街信号输入双稳系统会因为不匹配而无法产生随机共振,为此在信号输入双稳系统前加入调制模块,该模块以外加调制信号W(t)的幅值及频率为调控变量,采用多参数调节方式使涡街信号产生随机共振,原理图如图1所示。
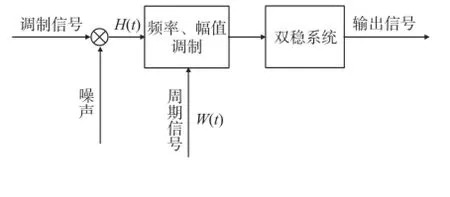
图1 调制随机共振原理图
图1中涡街信号H(t)由周期信号A0cos(2πf0t)及噪声Г(t)组成,在输入双稳系统前由信号W(t)= Accos(2πfct)进行频率及幅值的调制,其中Ac为幅值调制参数,fc为频率调制参数,调制过程可用式(4)表示。
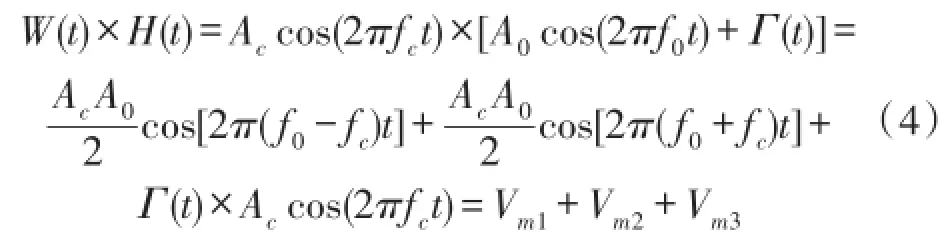
H(t)经过调制可分为Vm1、Vm2、Vm3三项,信号的频率及幅值都发生变化。其中Vm1项频率为f0-fc,记为Δf,调节fc可以使Δf减小,使Vm1项频率小于逃逸率RK,Vm2项频率为f0+fc,相比Vm1项频率较高,Vm3项是调制后的白噪声,文献[14]指出白噪声经过余弦信号调制后仍然为白噪声,在双稳系统的作用下,信号频率越低,系统输出的功率谱值越大[14],因此经过调制,Vm1将在输出中占主导作用,双稳系统将产生与Vm1项频率Δf同频的输出。在信号幅值匹配的条件下,通过调节fc可以使信号频率Δf<RK,实现频率的匹配,使系统产生随机共振。
信号幅值与系统的匹配有两种方式,一是改变信号幅值A0,二是调整系统参数μ,改变系统阈值At。调整系统参数μ时会改变系统的势垒高度ΔU=μ2/4,当信号幅值A0较小时,调整μ的方法会导致势垒过低,系统的双稳态特性消失,随机共振效应变弱。因此处理幅值变化较大的涡街信号时,改变信号幅值匹配方式更为适用。如式(4)所示,通过W(t)及参数Ac对信号进行幅值调制,特别是对系统输出影响最大的Vm1项进行幅值调制。Vm1项幅值调制后信号幅值由A0放大Ac/2倍记为A1,A1=AcA0/2,改变调制参数Ac可以调整A1的大小,实现信号幅值与系统阈值的匹配。
可见,涡街信号经过调制后,输出信号幅值和频率可以与双稳系统匹配,产生随机共振。
1.3双调制随机共振数值仿真
输入信号如图2(a)所示由f0=10 Hz、A0=0.01的周期信号及噪声强度D=0.01的高斯白噪声叠加而成,从时域图中可见信号幅值较小,没有明显周期性,从频域图中几乎不可见周期信号成分。对于μ=1的双稳系统,该信号频率及幅值都不满足匹配条件,直接输入系统难以产生共振。使用fc=9.995 Hz,Ac= 60的调制信号W(t)对该信号进行调制,再输入双稳系统,得到系统输出结果如图2(b)所示,时域图中可见系统输出中产生了随机共振,信号展现出明显的周期性,频域图中可见输出的功率谱峰值位于Δf= 0.005 Hz处,与调制频率fc相加得到输入信号频率Δf+fc=10 Hz,且信号谱值为0.56,与共振前相比显著增长。该结果说明通过外加调制信号可以有效实现信号与系统的匹配,使系统输出中产生随机共振。
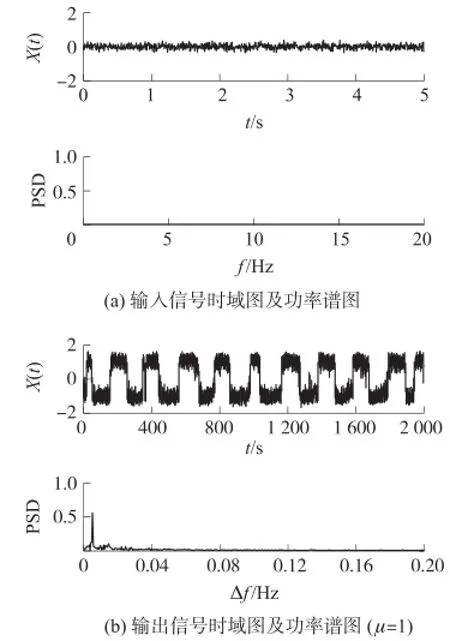
图2 输入输出信号时域图及功率谱
2 调制参数的选取
2.1不同调制参数下的系统响应
对输入系统的信号进行频率及幅值的调制,可以使信号与双稳系统实现匹配并产生随机共振现象,但对于特定信号,只有频率参数和幅值参数满足条件的调制信号才能达到匹配目的,为此对调制参数对系统输出的影响做进一步研究。
2.1.1频率调制参数
图3是调节参数fc得到的Δf与输出功率谱中Δf处谱值大小的关系曲线,可见随着Δf逐渐增大,输出功率谱值迅速减小,说明当调制参数fc的值逐渐远离信号频率f0的值时,输出中的共振效应很快就会削弱甚至消失。因此在频率调制过程中,只有将参数fc调节至f0附近的小范围内(图中为f0±0.05 Hz),系统才能产生随机共振。面对频率未知的实测信号时,如何准确选取参数fc是产生共振的关键之一。

图3 频率调制时的输出功率谱值变化
2.1.2幅值调制参数
图4是调节参数Ac得到的Ac与输出功率谱中信号谱值大小的关系曲线,可见随着Ac逐渐增大,信号谱值经历了从小到大再逐渐减小的过程。在此过程中,当Ac较小时,调制后的幅值A1远小于系统阈值At,输出无法越过势垒,在单势阱中运动,因此输出信号功率谱值较小,当Ac逐渐增大至图中Ac=45~50时,幅值A1与阈值At匹配,系统产生随机共振增强信号,使输出信号功率谱值增大,当Ac继续增大时,幅值A1大于阈值At,此时噪声直接越过势垒,作用到输出端,使信号功率谱值逐渐减小,因此幅值调制参数Ac在调节过程中存在最优值,且与系统能否产生共振有直接关系。根据图4的关系曲线,可将幅值与阈值匹配的条件设为A1=kAt,其中k为匹配系数,为满足共振条件A1小于At,k设置范围为0.5<k<1,一般设为0.8。在系统参数μ一定的条件下,根据可求得阈值At,而A1=AcA0/2,计算出信号幅值A0的大小就可以对参数Ac进行调节。在测量过程中,在A0未知情况下,如何确定Ac是关键点也是难点。
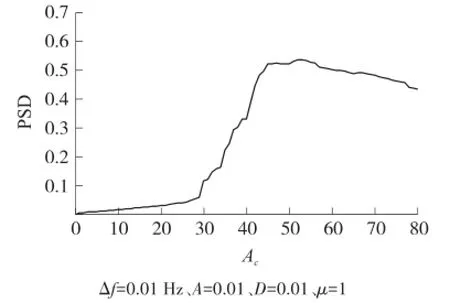
图4 幅值调制时的输出功率谱变化
综上,经过调制后的信号频率及幅值大小满足前文指出的双稳系统与输入信号匹配条件时,就能产生良好的随机共振现象,但能够满足条件的调制参数都与实际信号的频率及幅值有关,且其中频率调制参数范围较小。因此在处理实际信号时,如何准确选取调制参数fc、Ac、是关键。
2.2基于标准差的调制参数范围选取方法
在实际的流量检测时,涡街信号的频率f0、幅值A0随流量的变化范围较大,对应的调制参数fc、Ac的选取较困难。因此本文根据涡街信号标准差中包含的流动信息,估计信号频率及幅值,进而缩小调制参数选取的范围,以便快速找到最优调制参数。
涡街流量计大多通过压电传感器测量漩涡压力的周期变化,流速稳定时,获取的信号近似余弦信号[4]。信号频率f与流体平均速度V之间关系如式(5)所示:

式中,Sr为斯特劳哈尔数,d为发生体迎流面宽度。可见频率f与流速V之间成正比关系,通过信号频率f可以直接确定流速V,反之亦然。涡街信号幅值代表漩涡升力大小,而漩涡升力FL与流速V之间的关系如式(6)所示:
式中,CL为流量计升力系数,ρ为流体密度。可见升力FL与流速V的平方成正比关系,升力由传感器转换为信号幅值,因此信号幅值A0包含有流速V的信息,通过幅值可以估计流速的大小。但现场涡街信号中叠加了噪声,使幅值在计算时存在较大偏差,且计算过程较为繁琐,尤其是小流量时,信号被噪声淹没的条件下,信号幅值难以计算。
涡街信号理想情况下近似于余弦信号,对于正弦以及余弦信号,信号的标准差与幅值之间存在一定联系。根据标准差的计算公式,经过化简、积分,可以得到理想余弦信号标准差与幅值的关系如式(7)所示:

式中,Ai为信号瞬时幅值,A¯为信号平均值,N为一个周期内的采样点数,N趋向无穷。可见余弦信号幅值与标准差成正比关系,因此涡街信号中可以使用标准差代替幅值对流速进行估算。根据式(6)中给出的二次关系以及实测数据,可以建立标准差与流速的二次多项式模型,通过模型可以直接利用信号标准差估计流速V的大小,根据式(5)将流速转换为频率f0,作为频率调制参数fc的参考,确定频率调制参数fc的选取范围,进行频率调制。
同时,如式(7)所示,通过标准差可以直接计算得余弦信号的幅值,因此在常规流速条件下,也可以计算得到较准确的涡街信号幅值A0,结合A1与系统阈值At的匹配关系,就可以确定幅值调制参数Ac范围。但随着流量减小,计算结果将逐渐产生偏差。因为小流量时,噪声的波动对标准差的影响增大,使标准差大于实际漩涡波动引起的标准差,得的幅值A0相比实际信号稍大。因此小流量条件下,将Std对应的幅值记为最大值,Std的五分之一对应的幅值记为最小值,得到涡街信号幅值A0范围为A0∈/5*Std,2*Std]。再根据匹配关系确定参数Ac的调节范围,根据共振结果逐渐缩小Ac的范围,进行幅值调制。
信号标准差是信号的统计参数,计算方便,通过标准差估算流体流速可以快速确定调制幅值和频率参数,便于实时处理涡街信号。
3 实验结果与分析
通过理论和仿真分析,双调制随机共振方法是信号处理的有效方法之一,但对实际涡街信号处理的有效性还需要通过实验进行研究。因此,搭建涡街流量计实验装置,实时采集涡街流量计输出的叠加现场噪声的旋涡波动信号,特别是小流量条件下涡街信号,探讨双调制随机共振方法以及调制参数选取方法应用于涡街信号处理的可行性和有效性。
3.1实验装置及模型建立
图5为涡街流量信号采集的实验装置,装置通过水泵将水从蓄水池抽入实验管道,流经稳压罐稳定水压,再由管道流经电磁流量计及涡街流量计,最后流回蓄水池,流速大小由水泵的变频器和管道中的调节阀控制。其中电磁流量计作为标准表给出参考值,不确定度0.2,涡街流量计为国内某厂家生产,精度1.0,管道口径50 mm,斯特劳哈尔数为0.1670。设置采样频率fs=500Hz,采集得表1中各流速时的信号,构建标准差Std及流速之间的关系模型,表1中流速大小通过电磁流量计给出,标准差通过数学方法计算得到。
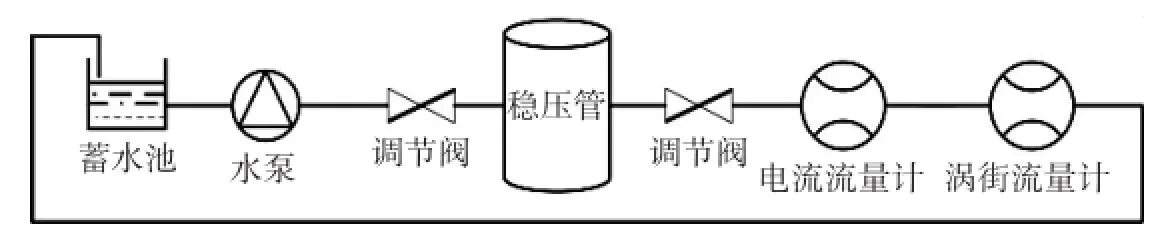
图5 实验装置示意图
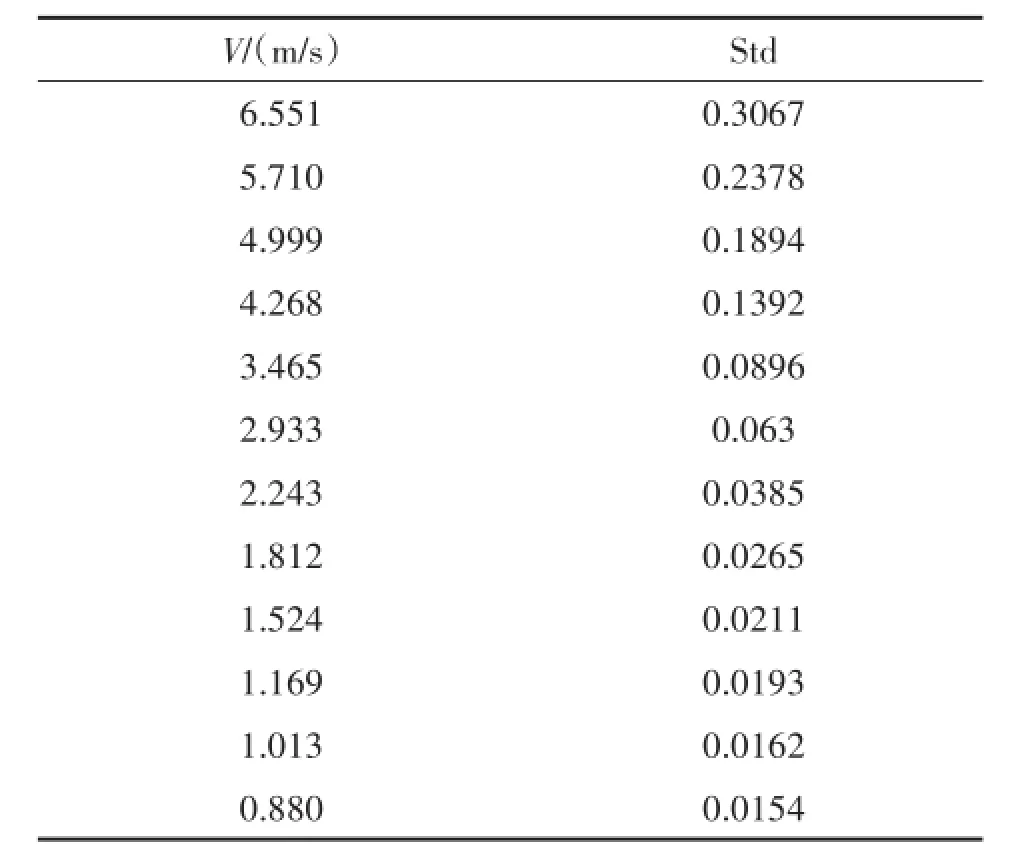
表1 各流量点涡街信号的标准差
根据表1中数据对流速与标准差的关系进行曲线拟合。拟合常规方法是在定义域上应用基函数对数据拟合,根据式(6)中升力与流速的关系,将标准差与流速的基函数设为二次多项式,如式(8)所示。
曲线拟合结果如图6所示,其中p1=0.007 073,p2=0.006 626,相关系数为0.998 7。利用式(8),就可以通过信号标准差给出流速的估计值,进而根据式(5)给出信号频率的估计值。
从图6可见当Std<0.025时,标准差随流速的变化较小,此时噪声在计算过程中的影响相对更大,计算得到流速容易偏差,因此将信号按标准差分为两类,Std>0.025时,视为常规流量信号,Std<0.025时,信号视为小流量信号。
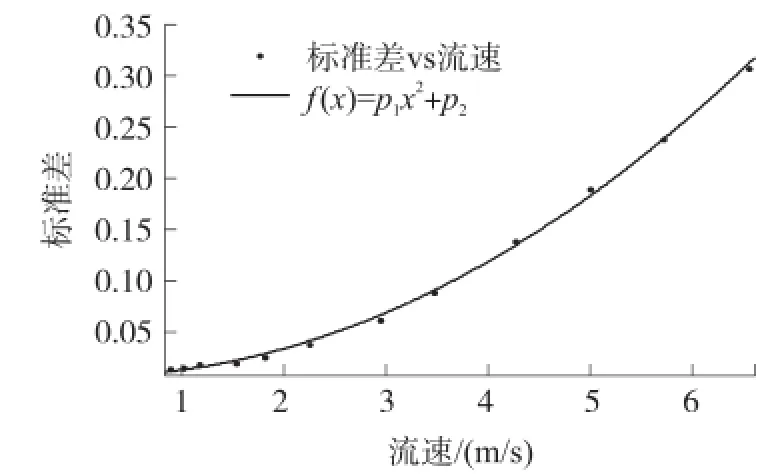
图6 流速与标准差的拟合关系
3.2数据处理与分析
采集常规流量及小流量涡街信号,进行实验分析,设置非线性双稳系统参数μ=0.5。
采集得一般流量下信号标准差为0.036 1,根据拟合关系求得流速估计值为2.045 m/s,由式(5)求得频率f0估计值为37 Hz,由式(7)求得信号幅值A0估计值为0.051 1,根据匹配关系,设置调制参数fc范围为(37±5)Hz,Ac范围为10±5。在该范围内连续改变参数fc,观察输出功率谱峰值的变化曲线,根据结果再进一步调节Ac,最终在Ac=12,fc=(37±5)Hz时,得到输出功率谱峰值随fc变化的曲线如图7所示,在fc=37.93 Hz时,功率谱的峰值显著增大,在该点的系统输出时域及功率谱图如图8所示,时域图可见系统输出产生了明显的共振现象,功率谱图中可见产生共振时Δf= 0.003 93 Hz。因此该涡街信号频率f0=fc+Δf为37.93 Hz,根据式(5)求得流速大小为2.106 m/s,转换为流量大小14.88 m3/h,与标准表电磁流量计显示流量14.89 m3/h相符合,说明常规流量时检测结果准确。
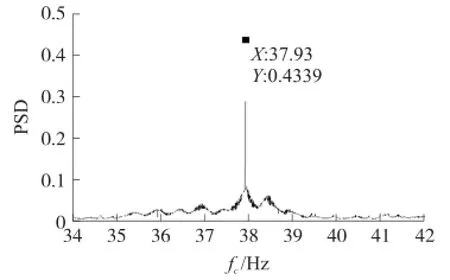
图7 输出功率谱峰值随fc的变化曲线
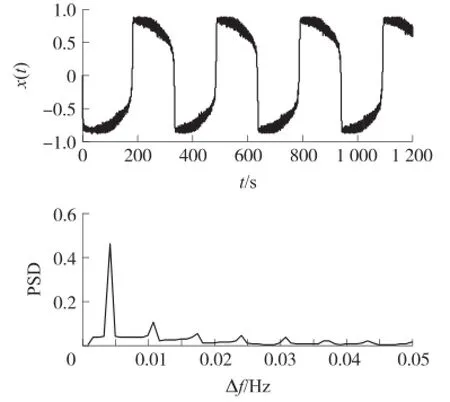
图8 双稳系统输出时域图及功率谱图
在小流量条件下,涡街信号更弱,一般信号处理难以获取涡街频率,因此特别选取小流量信号进行实验。采集得小流量信号标准差为0.0162,根据拟合关系求得流速的估计值为1.062 m/s,由式(5)得到频率f0的估计值为20 Hz,由式(7)得到信号幅值A0的估计范围为[0.0229,0.0045],根据匹配关系,设置调制参数fc范围(20±10)Hz,Ac范围为[23,115]。在该范围内连续改变参数fc,观察输出功率谱峰值的变化曲线,根据结果再进一步调节Ac,最终在Ac=110,fc=(20±10)Hz时,得到输出功率谱峰值随fc变化的曲线如图9所示,发现fc=13.25 Hz时,功率谱峰值显著增大,在该点的系统输出时域图如图10所示,时域图中可见系统输出产生了明显的共振现象,功率谱图中可见发生共振时Δf=0.005 44 Hz。因此该小流量段涡街信号频率f0=fc+Δf为13.25 Hz,根据式(5)求得流速大小为0.718 m/s,转换为流量大小为5.07 m3/h,与标准表电磁流量计显示流量5.10 m3/h相符,说明小流量时检测结果准确。
实验结果表明通过标准差对实际涡街信号频率、幅值进行估计是有效的,可以提高涡街信号与非线性双稳系统的匹配效率。经过双调制的涡街信号输入系统产生随机共振现象与理论分析及数值仿真中获取的结果一致,说明双调制随机共振处理实际涡街信号,特别是弱涡街信号是可行和有效的。
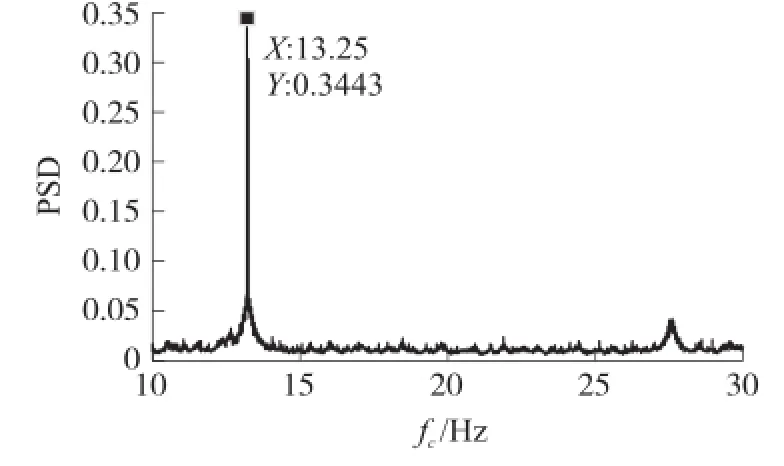
图9 输出功率谱峰值随fc变化曲线

图10 双稳系统输出时域图及功率谱图
4 结论
输入信号与双稳系统的匹配对系统产生随机共振十分关键。利用外加频率及幅值可调的信号进行双重调制是实现信号与系统匹配的有效方法。利用涡街信号的标准差及其与信号频率、幅值之间的关系可以给出频率及幅值的估计值,以此作为依据可以极大的缩小调制参数的选取范围,提高涡街信号与系统匹配效率,为涡街信号的检测提供了新的方法,同时该方法可适用于其他涉及强噪声中的信号检测领域,对拓宽随机共振应用范围,解决工程实际问题具有重要意义。
[1]贾德利,于泳,陈召,等.分层注水工艺中涡街流量计信号处理方法研究[J].传感技术学报,2015,10:1513-1519.
[2]王慧,黄咏梅.带狭缝圆柱钝体流量测量特性研究[J].传感技术学报,2013,12:1661-1665.
[3]孙宏军,徐冠群.基于相角判据的Rife算法的涡街信号处理方法[J].仪器仪表学报,2013,34(12):2860-2 866.
[4]郑德智,王帅,樊尚春.涡街流量传感器信号处理方法研究[J].传感技术学报,2009,01:80-84.
[5]江文斌,秦会斌,邵李焕,等.基于经典谱估计改进方法的涡街流量计[J].仪器仪表学报,2012,33(1):229-234.
[6]Xu,Luo,Wang,et al.Frequency-Feature Based Antistrong Cistur⁃bance Signal Processing Method and System for Vortex Flowmeter with Single Sensor[J].Review of Scientific Instruments,2010,81(7):075104-075104-7.
[7]惠国华,陈裕泉.随机共振信噪比谱分析方法及其初步应用研究[J].传感技术学报,2010,08:1134-1136.
[8]Locher M.,Inchiosa M.E.,Neff J.,et al.Theory of controlling sto⁃chastic resonance[J].Physical review E,2000,62(1):317-327.
[9]Mason J,Lindner J F,Neff J,et al.Pulse-Enhanced Stochastic Resonance[J].Physics Letters A,2000,277:13-17.
[10]Kohar V,Murali K.Sudeshna Sinha.Enhanced Logical Stochastic Resonance Under Periodic Forcing[J].Communications in Non⁃linear Science and Numerical Simulation,2014,19:2866-2873.
[11]Qin,Tao,He,et al.Adaptive Bistable Stochastic Resonance and its Application in Mechanical Fault Feature Extraction[J].Jour⁃nal of Sound&Vibration,2014,333(26):7386-7400.
[12]樊养余,李利品,党瑞荣.基于随机共振的任意大频率微弱信号检测方法研究[J].仪器仪表学报,2013,34(3):566-572.
[13]PETER J,FABIO M.Energetics of Stochastic Resonance[J]. American Institute of Physics,2011,21,047516.
[14]林敏,毛谦敏,郑永军,等.随机共振控制的频率匹配方法[J].物理学报,2007,56(9):5021-5025.

丁君鸿(1992-),男,2013年于中国计量学院现代科技学院获得学士学位,现为中国计量学院在读硕士研究生,主要研究方向为信号分析与处理,iceqingwa@ foxmail.com;

黄咏梅(1967-),女,1988年于浙江大学获得学士学位,1991年于中国计量科学研究院获得硕士学位,2005年于浙江大学获得博士学位,现为中国计量学院教授,主要研究方向为流量检测技术,ymhuang@ cjlu.edu.cn。
Vortex Signal Detection Method Based on the Dual Modulated Stochastic Resonance*
DING Junhong,HUANG Yongmei*,LIN Min
(College of Metrology and Measurement Engineering,China Jiliang University,Hangzhou 310018,China)
A signal processing method based on stochastic resonance applied to the vortex shedding frequency mea⁃surement of vortex flowmeter is studied.The relationship between signal and bistable system parameters such as threshold value and Kramers rate is discussed.The input signal is dual modulated by the signal with adjustable am⁃plitude and frequency to realize the matching between signal and bistable system.The simulation results manifest that the matching method is feasible and effective.The method specific to vortex signal is proposed to selecting mod⁃ulation parameters based on the standard deviation.The vortex signal feature is used to estimate the flow velocity and reduce the modulating parameters scope by standard deviation.Therefore,the matching efficiency between sig⁃nal and bistable system is improved.The experimental results indicate that the modulated method can make the vor⁃tex signal,especially the weak vortex signal generate stochastic resonance and effectively obtain the frequency of vortex shedding for flowrate measurement.
signal processing;stochastic resonance;signal modulation;vortex flowmeter;
TH814
A
1004-1699(2016)05-0723-06
项目来源:浙江省自然科学基金项目(LY13E050012)
2015-11-09修改日期:2016-01-26

