弧底梯形渠道无喉道量水槽水位流量关系数值模拟
钟新铭, 马孝义, 杨珮珮
(西北农林科技大学 水利与建筑工程学院, 陕西 杨凌 712100)
弧底梯形渠道无喉道量水槽水位流量关系数值模拟
钟新铭, 马孝义, 杨珮珮
(西北农林科技大学 水利与建筑工程学院, 陕西 杨凌 712100)
目前为适应我国多数渠道断面方式和灌区管理方式,开发研制新型量水配套设施对灌区节水起着至关重要的作用。利用Fluent 6.3大型流体力学数值仿真软件,结合有限体积法、RNG k-ε湍流模型和VOF模型,在不同渠道底坡上对不同量水槽水位流量进行数值模拟试验研究。结果表明:(1) 量水槽流态上游水面平稳属于缓流,量水槽槽内水流为急流,可知由缓流过度到急流必然会发生临界流,量水槽沿程弗劳德数可知量水槽喉口附近扩散段内产生临界流;(2) 弧底梯形渠道无喉道量水槽具有较好的水位流量关系,渠道收缩比ε与渠道比降i对形成单值稳定的水位流量关系有较大的影响,随着渠道尺寸增大同时收缩比ε减小,量水槽水位流量逐渐在较大的底坡范围内形成统一的水位流量关系。(3) 流量系数与量水槽宽和收缩比具有较好的线性关系,同时流量系数随R,H、ε的增大而变大,回归分析建立的量水槽流量公式,测流公式平均误差值小于5%,说明弧底梯形渠道无喉道量水槽测流是可行的,满足明渠测流要求。研究成果对灌区渠道量水槽的设计优化提供了一定的参考和建议。
节水灌溉; 量水槽; 数值仿真; 渠道底坡
近年来大量学者对量水槽开发设计进行了物理试验和数值模拟试验,大多针对单一渠道不同流量工况下量水槽收缩比进行研究,所得研究结果很难推广应用,量水槽应用尚需在不同底坡明渠均匀流条件下进行综合试验研究,从而得到选型设计依据[1]。王智等[2]利用Fortran自编程对U形渠道抛物线形量水槽在不同底坡条件下进行水力电算模拟,分析了不同收缩比下的水位流量关系,通过模拟水位流量数据得到了流量系数的经验式,建立了统一的水位流量公式,随后,吕宏兴等[3]在其研究基础上分析了对量水槽进行选型设计,得到底坡与收缩比的关系。马孝义等[4]在前人对U形渠道量水槽研究的基础上,对量水槽在不同底坡渠道条件下进行计算机模拟,对量水槽进行了筛选研究,得到抛物线型量水槽性能相对于其他量水槽较好。刘英等[5]通过室内模型试验分析了圆头量水槽在不同底坡条件下的水位流量关系,建立了具有量纲和谐流量公式。这些研究对开发量水槽设计选型以及渠道量水作出了很大的贡献,但是自编程只能计算水面线不能得知整个量水渠槽的流场变化,同时物理模型试验试验易受物理模型局限,研制周期长、人力物力投入大。相对物理模型试验,CFD技术以其高效低成本,能够提高新型量水设施的研发效率[6-9],使系统的分析量水渠槽在不同底坡明渠均匀流条件下进行数值试验研究成为可能。弧底梯形断面具有抗冻胀,水力条件好,不易淤积,且容易复位等特点,在北方灌区应用非常广泛[10]。本文针对弧底梯形设计弧底梯形渠道无喉道量水槽,采用RNG k-ε湍流模型和VOF方法对量水槽进行数值模拟,对量水槽在不同底坡均匀流条件下进行综合仿真模拟试验研究,以期为量水槽设计选型及优化提供依据。
1 弧底梯形渠道无喉道量水槽
1.1量水槽物理模型
弧底梯形渠道无喉道量水槽结构:弧底梯形渠道无喉量水槽由进口收缩段,呈3∶1收缩,出口扩散段,呈6∶1扩散,两部分组成,笔者针对弧底梯形渠道断面特点,提出了弧底梯形渠道无喉量水槽收缩比ε的概念即调整喉口断面弧底半径R、渠深H、边坡系数m,使得量水槽形成侧收缩的喉口断面面积A0与渠道断面面积A之比,即ε=A0/A。弧底梯形渠道断面无喉量水槽结构如图1所示,B为渠道顶宽,W为喉宽,h为渠槽水位。
1.2理论公式
弧底梯形渠道设计流量Q设为设计水位下不同断面尺寸、糙率、底坡时的渠道流量,可按式(1)计算,由连续性方程和谢才经验公式组成:
(1)
式中:Q设——渠道设计流量;A,V——弧底梯形渠道面积及渠道流速;C——谢才系数,与断面形状、尺寸及边壁糙率n有关;i——渠道底坡。弧底梯形渠槽具体尺寸设计可见表1。

图1弧底梯形渠道无喉道量水槽的结构示意图
1.3数值试验方案
为了确定较大尺寸范围弧底梯形渠道无喉段量水槽的全面特性,克服标准流量实测困难,设计了数值模拟仿真试验。本试验的目的是对不同规格尺寸的量水槽在不同底坡明渠均匀流条件下进行综合试验数值模拟,以期得出无喉量水槽在弧底梯形渠道上应用的可行性分析,并在此基础上,找出这种新型量水设施的水力特性和测流规律,提出初步的设计方法。表1为弧底梯形渠道及量水槽数值试验方案。研究内容包括:(1) 分析量水槽流态以及临界流发生位置;(2) 分析不同收缩比、底坡条件下的水位流量变化规律;(3) 分析建立量水槽流量公式以及流量系数变化规律。
2 湍流数值计算方法
2.1基本控制方程
时均化的Reynolds方程,被简称为雷诺平均法(RANS)。湍流时均运动基本方程如下:
(2)
(3)
要使方程组封闭,必须对Reynolds应力项作出某种假定,即建立应力的表达式或引入新的RNGk-ε湍流模型方程。

表1 弧底梯形渠道无喉道量水渠槽数值试验方案
紊流动能k方程:
(4)
紊流动能耗散率ε方程:
(5)
式中:ρ,μ——体积分数平均的密度和分子粘性系数;μt——湍动粘度,可由k、ε求出:
(6)
Gk为由平均速度梯度引起的紊动能产生项:
(7)
在ε方程中增加了一项时均应变率Eij:
(8)
式中:αk=αε=1.39,Cμ=0.0845,C1ε=1.42,C2ε=1.68,η0=4.377,β=0.012。
2.2三维模型建立
利用AUTOCAD 2010建立弧底梯形量水渠槽三维模型,量水槽结构见图1,弧底梯形无喉量水渠槽尺寸见表1,为了逼真的模拟渠道流态,减小上下游边界对计算域的影响,模拟选取渠道长25 m左右,渠槽建模时取顺水流方向为x轴(顺水流为正),宽度方向为y轴(渠道左岸为正),高度方向为z轴(向上为正),坐标原点取在渠道进口断面(x=0)圆弧中心处。以量水槽为零点,不同水位流量工况下,上游取10~15 m,下游取15 m。
2.3网格划分与边界条件
联合gambit进行网格划分,边界条件设置。为了准确的还原真实的弧底梯形无喉量水槽过流过程,以及便于后处理过程中分析与计算,将数值模型分割为3部分,量水槽上游进口渠道段,量水槽段,量水槽下游出口渠道段。进口渠道段与出口渠道段由于流态稳定而且结构简单,选择直接生成可以构造多种算法且以六面体网格单元为主的结构化网格,中间无喉量水槽部分由于会发生湍流,流动域结构较为复杂,选择灵活性与自适应性较高的四面体与六面体、楔形和锥形网格单元相结合的非结构网格,并对该部分网格进行局部加密。在量水槽段采用非结构网格,渠道段采用结构网格单元进行剖分,因渠道左右对称,可取一半计算域,网格总数约4.5×105个单元。
量水槽进口边界分别由空气进口和水流进口二部分组成,空气进口边界条件设置压力进口边界,水流进口给速度进口边界,水流进口给出水深H、进口断面平均流速u0,湍动能k和湍动能耗散率ε,两者按照公式(9)计算,量水槽数值模拟边界条件参数设置见表2。
k=3(Iu0)2/2
I=u′/u均=0.16(ReD)-1/8
(9)
式中:u0——进口处的平均流速;I——紊流强度;ReD——按照水力直径D计算得到的雷诺数。Cμ——常数,取0.09;l——紊流长度,l=0.07L;L——关联尺寸,取水力直径。
3 弧底梯形渠道无喉道量水槽数值模拟
3.1量水槽流态分析
整个模拟在水平的和有坡的渠道进行,初始流场中充满气体,根据各个水位流量工况对数值模型进行预处理初始化流场,采用RNGk-ε湍流方程封闭雷诺时均N-S方程,基于VOF方法跟踪自由表面,对离散方程组的压力速度耦合采用PISO算法,水流从入口流入渠槽直至出口,通过对体积分数的迭代求解,就能够自动生成水气的交界面,设置监视器中Mass Flow Rate选项,当其值接近于0且基本保持不变,认为计算收敛。
采用CFD软件之Fluent 6.3对建立好的三维模型进行仿真计算。

表2 底坡i=1/1 000,1/2 000范围内模型边界条件参数设置表
在自由出流时,量水槽上游流线稀疏且相互平行,水流较缓;在量水槽收缩段,由于受到渠道边壁侧收缩的影响流线开始在渠道中间拥挤,在流道内水流开始向下弯曲,产生跌水;在量水槽扩散段,水面大幅下降,流线变形较大,水面在量水槽出口处附近降至最低;在量水槽下游渠道一定距离流线又恢复到平稳状态。
对应的沿程弗劳德数如图2所示,量水槽上游在15 m以前,水面平缓,可以看出弗劳德数Fr小于0.5,属于缓流,满足量水槽测流要求;量水槽范围在15~20 m内,由于水面跌落,流速加快,可知看出弗劳德数Fr变化幅度较大,由小于1变化到大于1,并在量水槽出口达到最大值;随后,量水槽下游经过一段距离,流速在下游逐渐减小,水流恢复成缓流,弗劳德数Fr小于1。从量水槽弗劳德数沿程数值变化可以看出,在喉口附近量水槽扩散段内发生临界流,此时弗劳德数Fr=1,后进入急流状态,与下游渠道水流衔接,下游在相当大的水深范围对上游水流无干扰,量水槽具有较稳定的水位流量关系,过槽流量只与槽前水深和量水槽的几何尺寸有关。

图2沿程佛汝德数Fr
3.2不同条件下量水槽水位流量关系研究
3.2.1不同收缩比对水位流量关系的影响数值试验取得的不同渠槽尺寸条件下的水位流量关系,成果如图3所示,不同收缩比ε对量水槽自由出流流量Q影响较大,在流量Q相同的情况下,收缩比ε越大,量水槽通过的流量Q就越大,过流能力就越大,壅水较小,对应的上游水深h相对较小。相反收缩比ε越小,量水槽通过的流量Q就越小,壅水较大,对应的上游水深h相对较大。

图3不同收缩比量水渠槽模拟水位流量关系
3.2.2不同底坡对水位流量关系的影响研究不同底坡对水位流量关系的影响,可知不同底坡是否对量水槽自由出流流量Q与上游水深h产生单值稳定的关系有影响,对R120渠道来说在底坡i=1/1 000~1/2 400研究范围内,上游水深h与流量Q相关性较好,如图4所示。水位流量关系如下所述:收缩比ε>0.74时,底坡i=1/1 000~1/1 200范围内难形成统一的水位流量关系;收缩比ε=0.74时,底坡i=1/1 000~1/1 200范围内能形成统一的水位流量关系;收缩比ε=0.69时,底坡i=1/1 000~1/1 600范围内能形成统一的水位流量关系;收缩比ε=0.65时,底坡i=1/1 000~1/2 000范围内能形成统一的水位流量关系;收缩比ε<=0.61时,底坡i=1/1 000~1/2 400范围内能形成统一的水位流量关系。对于不同渠道量水槽尺寸结构在不同渠道底坡范围内能形成统一的水位流量关系,成果见表1。可知,随着渠道尺寸增大同时收缩比ε减小,量水槽水位流量逐渐在较大的底坡范围内形成统一的水位流量关系。
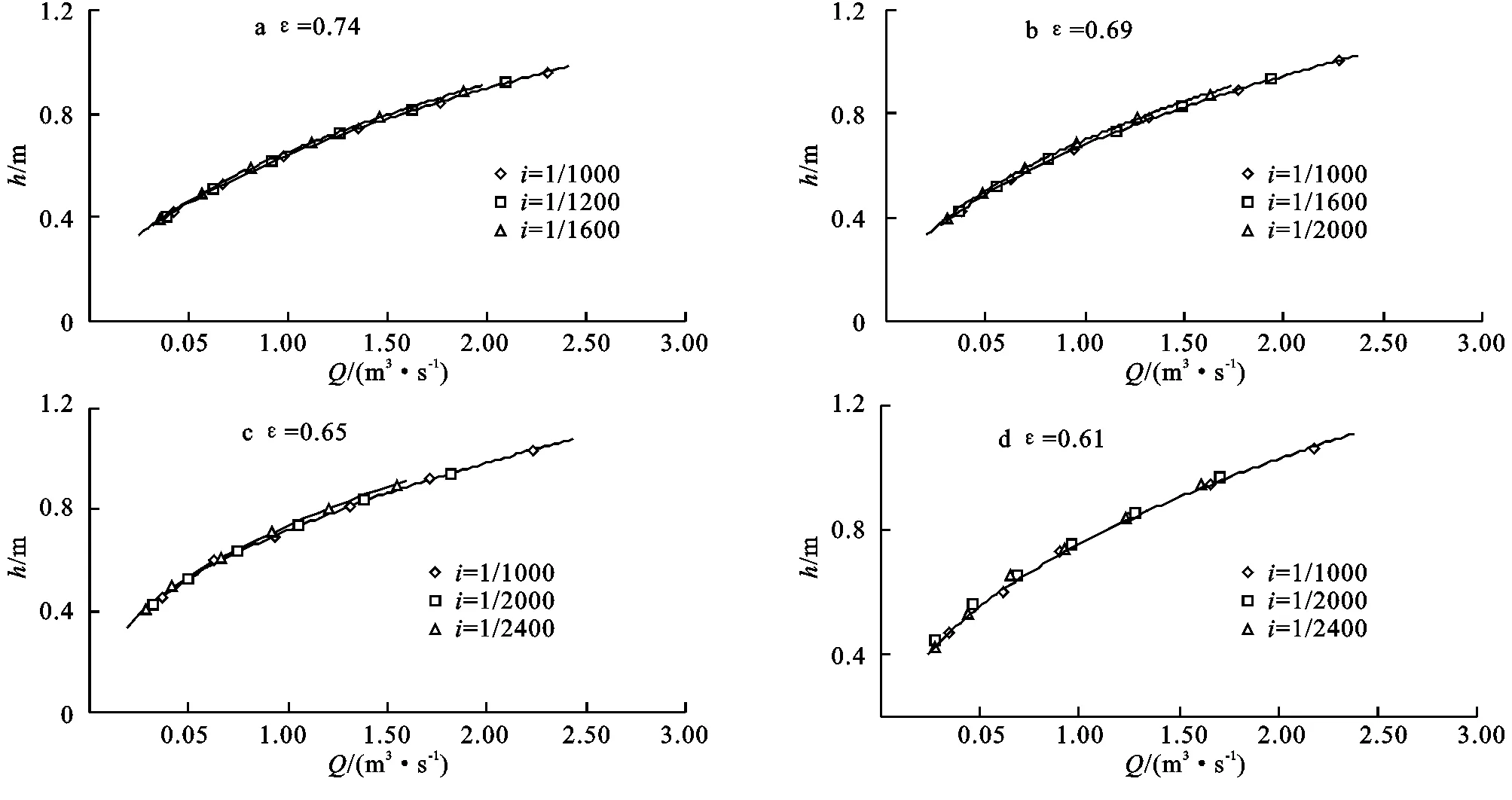
图4不同底坡量水渠槽模拟水位流量
3.3测流规律
3.3.1流量系数变化规律在较大参数范围内研究量水槽的过流特性及自由出流时流量系数的变化规律,探讨底弧半径R,渠深H,渠道边坡m,量水槽的收缩比ε,量水槽槽宽W,量水槽槽长L及渠道比降i,对量水槽流量计算的影响,具体量水渠槽参数见表1。量水槽基本流量公式为:
Q=C·hn
(10)
式中:Q——渠道流量(m3/s);C——自由出流流量系数;h——水位;n——自由出流流量指数。

图5收缩比、喉宽、自由流系数关系
对于不同尺寸的槽型,流量系数与喉宽,收缩比的关系如图5所示,流量系数与量水槽收缩比、量水槽槽宽具有较好关系,关系式如下:
C=K(εW)0.881
(11)
式中:K——自由出流槽长系数(m3/s);ε——量水槽收缩比;W——量水槽槽宽。
对不同渠道尺寸范围和不同收缩比的量水槽的水位流量进行数值试验,K,C,n部分拟合成果见表3,4。结果表明量水槽流量系数随着量水槽尺寸的增加而增加,流量指数随着量水槽尺寸的增加而减小,与矩形无喉道量水槽水位流量关系[11]研究结果相同。同时对于不同渠道尺寸的量水槽,流量系数随着R,H,ε的增加而增加。

表3 R120渠道弧底梯形无喉量水槽自由流系数与指数关系

表4 R180渠道弧底梯形无喉量水槽自由流系数与指数关系
3.3.2流量公式建立对不同渠道尺寸范围(弧底半径R=0.8~1.8 m,渠道高H=1.4~1.6 m,边坡系数m=1~1.5)和不同收缩比(0.61~0.74)的量水槽进行数值模拟,通过模拟水位流量数据得到流量系数变化规律,可知流量系数与收缩比和槽宽具有较好的关系,以此建立统一的水位流量公式。考虑数值试验模拟数据,进行逐步回归分析得到流量公式与量水槽结构尺寸的经验公式为:
Q=1.077(εW)0.881h2.2R2=0.996
(12)
式中:h——上游水深(m);W——量水槽喉宽(m);ε——弧底梯形无喉量水槽收缩比;Q——不同收缩比工况下的弧底梯形无喉量水槽的过流流量(m3/s),该公式测流范围为0.24~2.36 m3/s。
将数值模拟流量,公式流量计算值与渠道流量对比,由表5可知:数值模拟流量和渠道流量之间最大误差为6.24%,其余误差均在5%以内,且平均误差为2.55%,可知两者吻合较好,采用数值模拟弧底梯形无喉道量水槽的方法是合理可靠的;建立的量水槽流量公式计算值与渠道流量最大误差为7.04%,其余误差均在5%以内,且平均误差为3.09%,两者吻合较好,符合明渠测流要求。
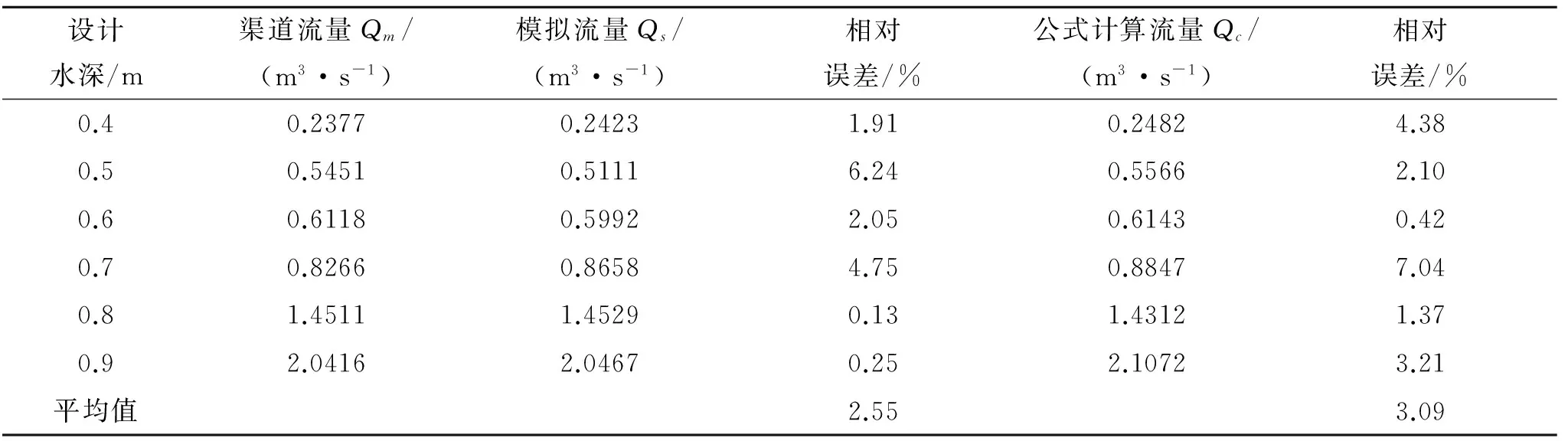
表5 渠道流量与模拟流量、公式计算流量对比
4 结 论
针对灌区弧底梯形渠道初步设计了与之相适应的无喉道量水槽,采用RNG k-ε湍流模型和VOF数值模拟方法,对弧底梯形渠道无喉道量水槽在不同底坡明渠均匀流渠道中进行三维数值试验。对沿程流态进行了分析,通过量水槽沿程弗劳德数可知在量水槽喉口附近扩散段内产生临界流。研究了不同渠槽结构参数组合对水位流量关系的影响,结果表明,渠道收缩比ε与渠道比降i对形成单值稳定的水位流量关系有较大的影响,随着渠道尺寸增大同时收缩比ε减小,量水槽水位流量逐渐在较大的底坡范围内形成统一的水位流量关系。分析了量水槽测流量规律,流量系数随着R,H、ε的增大而变大,通过回归分析建立的流量公式,测流公式平均误差值小于5%,表明弧底梯形渠道无喉量水槽测流是可行的,满足明渠测流要求。弧底梯形渠道无喉道量水槽初步设计研究结论可为量水槽设计优化及野外试验提供新的思路和参考。
[1]吕宏兴,余国安,陈俊英,等.矩形渠道半圆柱形简易量水槽试验研究[J].农业工程学报,2004,20(6):81-84.
[2]王智,朱凤书.平底抛物线形无喉段量水槽试验研究[J].水利学报,1994(7):12-23.
[3]吕宏兴,朱晓群,张春娟,等.U形渠道抛物线形喉口式量水槽选型与设计[J].灌溉排水学报,2001,20(2):55-57.
[4]马孝义,王文娥.U形渠道量水槽的性能分析与筛选研究[J].农业工程学报,2002,18(4):44-49.
[5]刘英,王文娥,胡笑涛,等.U形渠道圆头量水柱测流影响因素试验及模拟[J].农业工程学报,2014,30(19):97-106.
[6]郝晶晶,马孝义,王波雷,等.基于VOF的量水槽流场数值模拟[J].灌溉排水学报,2008,27(2):26-29.
[7]潘志宝.机翼形量水槽水力特性试验与数值模拟研究[D].陕西杨凌:西北农林科技大学,2009.
[8]孙斌,吕宏兴,潘志宝.矩形农渠机翼形量水槽水力特性数值模拟[J].干旱地区农业研究,2010,28(2):155-158.
[9]刘嘉美,王文娥,胡笑涛.U形渠道圆头量水柱的数值模拟[J].中国农业大学学报,2014,19(1):168-174.
[10]程亚利.弧底梯形渠道衬砌在宝鸡峡灌区更新改造中的应用[J].杨凌职业技术学院学报,2010,9(2):50-51.
[11]Skogerboe G V, Bennett R S, Walker W R. Generalized discharge relations for cutthroat flumes[J]. Journal of the Irrigation and Drainage Division, 1972,98(4):569-583.
Numerical Simulation on Discharge Relation of Arc-Based Trapezoidal Canal and Cut-throat Flow Measurement Flume
ZHONG Xinming, MA Xiaoyi, YANG Peipei
(College of Water Resources and Architectural Engineering, Northwest A&F University, Yang ling, Shaanxi 712100, China)
To adapt to the irrigation management methods and section form of most channels, developing new facilities plays a vital role in water-saving irrigation. According to finite volume method, RNG k-ε turbulence model and VOF model, we make the amount of three-dimensional numerical simulation experimental study on arc-based trapezoidal cut-throat flow measurement flume by Fluent 6.3. By comparing the simulation results with the theoretical value, the result is well matched. This proofs that the fluent software for numerical simulation methods of free surface turbulence characteristics is reliable. On this basis, we carry out the amount of comprehensive simulation experimental Study on water level and discharge in different open channel bottom slopes. The results show that: (1) the upstream of the flow measurement flume is slow steady stream and the internal flow is jet stream, so the critical flow is bound to happen, Froude numbers along the flow measurement flume show that the critical flow can generate near the diffusing section of the throat; (2) the relationship between upstream water level and discharge is significant, the contraction ratio and bottom slope have great impact on forming the stable relationship between water level and discharge, the contraction ratio decreases with the increases ofε, channel sizeR,H, flow measurement flumes gradually form the unified water level and discharge relationship in the larger scope of the bottom slope; (3) the results have shown that the flow coefficient has a linear relationship with flume width and contraction ratio, and the flow coefficient increases with an increases ofR,Hand ε. The flow equations established by regression analysis show the average error value formula for measuring flow within 5%, which explains that arc-based trapezoidal canal and cut-throat flow measurement flume meets the requirements of open channel flow measurement. The results will provide some
and recommendations for the application of the irrigation branch canals.
water-saving irrigation; flow measurement flume; numerical simulation; channel bottom slope
2015-04-27
2015-05-11
国家自然科学基金项目(51279167);“十二五”国家科技支撑计划项目(2012BAD08B01);“十二五”国家863计划项目(2011AA100509)
钟新铭(1987—),男,江西万安人,在读硕士,主要从事节水灌溉理论与新技术研究。E-mail:zxmhong55@163.com
马孝义(1965—),男,陕西凤翔人,教授,博士生导师,主要从事节水灌溉理论与新技术研究。E-mail:xiaoyima@vip.sina.com
TV135.3
A
1005-3409(2016)02-0340-06

