空化热效应对上游泵送机械密封润滑性能的影响
陈汇龙,王彬,任坤腾,李同,赵斌娟
空化热效应对上游泵送机械密封润滑性能的影响
陈汇龙,王彬,任坤腾,李同,赵斌娟
(江苏大学能源与动力工程学院,江苏镇江 212013)
机械密封端面空化现象是影响机械密封润滑性能的重要因素。采用计算流体动力学方法,基于Antoine公式,建立了考虑空化热效应的计算流体动力学模型,并与常用的仅考虑端面液膜粘温效应的模型进行对比,分析了空化热效应对密封性能的影响。结果表明:在低转速下,空化热效应的影响可以忽略,但在高转速下空化热效应使上游泵送机械密封的高压区形成能力减弱,泵送量降低,开启力降低;在高转速工作条件下分析密封失效机理时,除了考虑黏温效应之外,还要考虑空化热效应的影响;空化热效应使螺旋槽槽区局部温度比仅考虑黏温特性时稍高;考虑空化热效应时,动环端面空化发生程度最严重,由动环端面沿膜厚方向至静环槽底,空化区域越来越小,槽底空化区域最小,此规律与仅考虑黏温关系时相反。
机械密封;动压润滑;空化;热力学性质;计算流体动力学;模型;稳定性
引 言
非接触式液体机械密封端面间液膜的空化现象对液膜的承载力具有非常重要的影响,尤其在高转速情况下,受流体变速运动和内摩擦温升的共同作用,液膜空化及其对密封性能的影响更加突出,因此深入研究这种影响的机理和规律性具有重要的理论和实际意义。
密封端面间液膜的空化问题最早是由Findley[1]提出的。Jakobsson等[2-3]提出了一种自适应空化边界条件来求解Reynolds方程,即JFO空化边界条件,由于其符合质量守恒定律,经过Elord算法[4]的改进,使该边界条件应用的可行性大大增加。在动力润滑理论领域,求解基于雷诺方程并考虑空化问题的控制方程大多使用上述边界条件和算法或其演化形式[5-9]。
对于液膜空化的研究,离不开液膜压力和温度。Pascovici等[10]认为等黏度下得到的密封间隙温度高于变黏度下的温度,基于等黏度的热流体动力模型已不适用。Lebeck[11]认为热效应对密封性能产生的影响和其他因素同等重要。这是由于热效应改变了润滑介质黏度,导致密封环变形,以及有可能使液膜汽化,从而导致泄漏量增加或密封失效[12]。由于介质黏度对温度的敏感性,很多学者在建立密封润滑的热流体动力润滑模型时,考虑了黏温关系的影响。而空化时的饱和汽化压力同样也对温度非常敏感,但在运用JFO边界条件求解雷诺方程时,通常设定汽化压力为大气压力或一定值[5-9],尚未有研究者考虑热效应对饱和汽化压力的影响问题。
本文以螺旋槽上游泵送机械密封为研究对象,以水为介质,在考虑黏温关系的基础上,利用克劳修斯-克拉贝隆方程基于实验数据拟合得到的汽化压力随温度的依变关系,即Antoine公式[13],建立考虑空化热效应的计算流体动力学模型,研究不同转速下空化热效应对密封润滑性能的影响。
1 计算模型
1.1 物理模型
本文研究的螺旋槽上游泵送机械密封结构如图1所示,静环材料为硬质合金,动环材料为碳石墨。在静环端面开设螺旋槽,槽型线为对数螺旋线,如图2所示。由于g个螺旋槽沿周向均布,因此取1/g液膜作为计算区域,如图3所示。本文采用笛卡儿坐标系,设静环端面为-平面,圆心为坐标原点,沿膜厚指向槽底方向为轴正方向。螺旋槽几何参数和工况参数见表1。
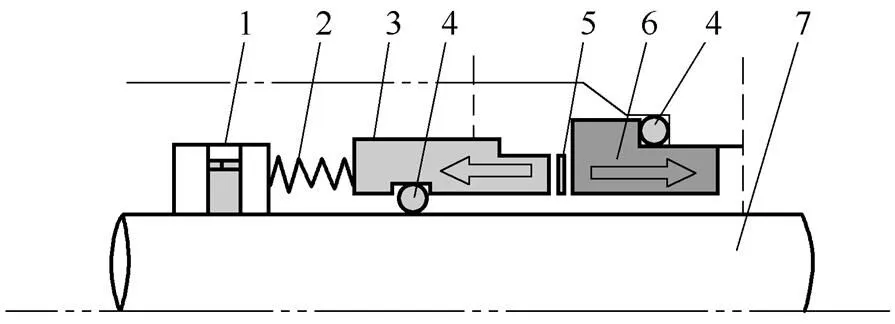
图1 密封结构示意图
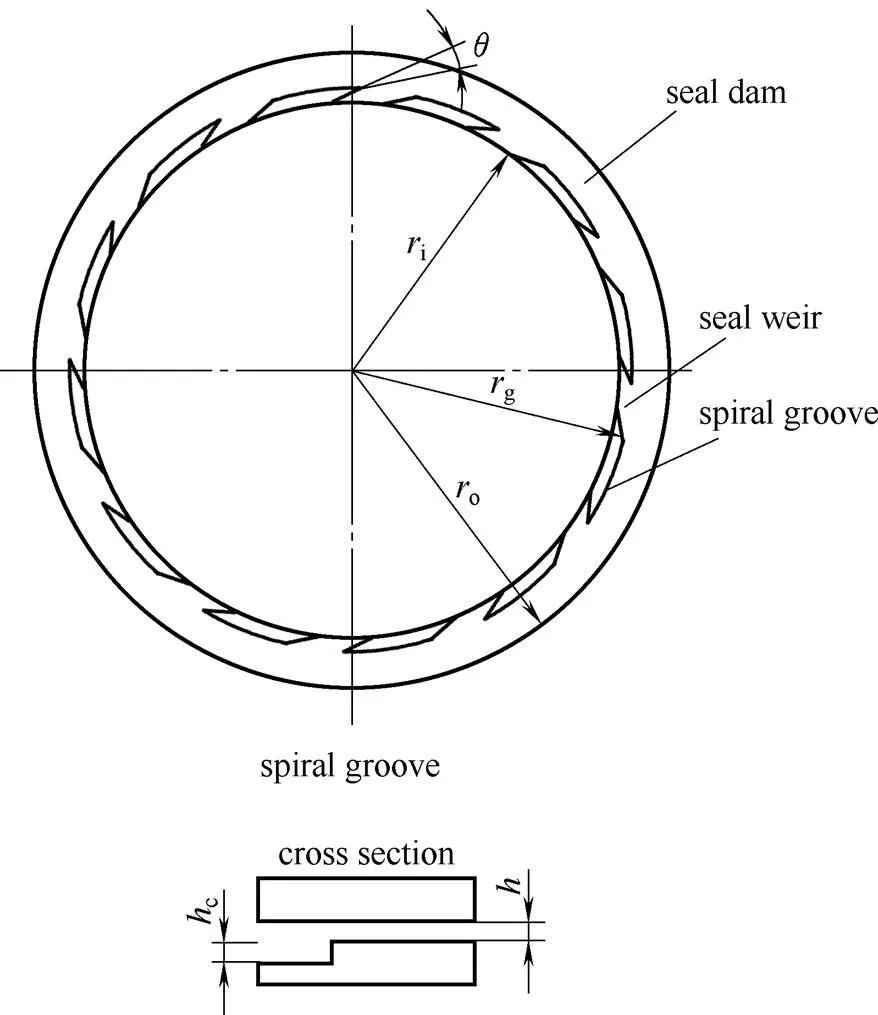
图2 静环端面螺旋槽结构

图3 液膜计算域
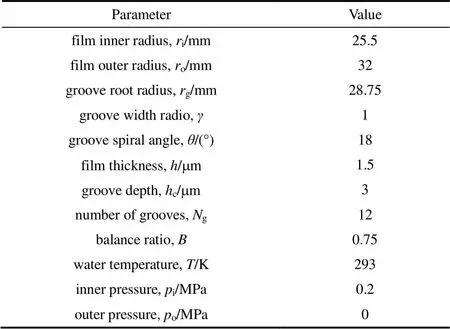
表1 密封面几何参数与工况参数
1.2 控制方程及数值求解
传统的雷诺方程是求解流体动压润滑问题的基本方程,但雷诺方程是由N-S方程简化推导而来的(如在液膜厚度方向忽略了压力及黏度变化的影响等),由于流场各参数之间的相互耦合作用,有可能使流场流动细节分析不能够准确把握,本文使用计算流体力学有限体积法,利用SIMPLEC算法对N-S方程、能量方程、气体输运方程、Reynolds黏温方程和Antoine公式进行求解,主要方程如下。
1.2.1 N-S方程 液膜流场采用如下N-S方程计算获得
1.2.2 气体输运方程 在空化过程中,液相和气相的质量传输由如下气体输运方程控制
式中,e和c分别代表空化过程中液相和气相之间的质量传输,可由描述单个气泡生长过程的Rayleigh-Plesset方程[14]推导得到,表述如下。


式中,v为饱和汽化压力。上述方程表明,当流场压力小于汽化压力时,气泡产生,空化发生,反之,气泡溃灭,空化消失。
1.2.3 能量方程
式中,S相为热源项,表示液膜中由于密封环转动产生的黏性摩擦热。
1.2.4 Reynolds 黏温方程[15]表征流体黏度随温度变化的关系为
1.2.5 Antoine公式 水的饱和汽化压力和温度的拟合曲线关系如图4所示,由图可见水的饱和汽化压力对温度非常敏感。本文利用克劳修斯-克拉贝隆方程,基于实验数据拟合得到饱和压力随温度的依变关系,即Antoine公式,如式(6)所示。
由上述方程及相应的边界条件建立考虑空化热效应的计算流体动力学模型。其中黏温方程和表征空化热效应的Antoine公式利用Fluent中的自定义函数(UDF)功能进行编程、编译,并嵌入到相应的接口。结合SIMPLEC算法,整个计算模型的求解程序如图5所示。

图5 计算流体动力学模型求解程序
求解上述方程,需使用离散格式建立离散方程。为了保证方程求解的精度及速度,动量方程和能量方程使用二阶迎风格式,气体输运方程使用QUICK格式。
1.3 边界条件
由于螺旋槽上游泵送机械密封端面间微尺度液膜沿端面轴对称分布,取图3中周期液膜为计算单元,其周期性边界条件为
空化边界条件为:当压力小于空化压力时,空化产生,空化泡内压力为饱和汽化压力值,空化泡壁压力梯度为0,即
为简化计算及保证一定的计算精度,假设液膜与动、静环端面的对流传热系数一致,并采用文献[16]的方法计算;忽略惯性力和热辐射的影响,不考虑端面微变形对温度、流场的影响。
1.4 对比模型
为了研究空化热效应对上游泵送机械密封润滑性能的影响,本文选取以下两种模型进行对比分析。模型1:只考虑黏温效应,即耦合Reynolds黏温方程,为一般热效应分析法;模型2:考虑黏温效应和空化热效应,即耦合Reynolds黏温方程和Antoine公式。
1.5 模型有效性检验
运用Gambit对单周期液膜进行网格划分,采用Pave方法生成四面形面网格,然后采用Cooper方法拉伸生成六面体体网格。为了保证模拟结果的可靠性,运用 5种网格划分方案进行网格划分,并针对工况为转速1000 r·min-1、进口压力0.2 MPa进行了两种对比模型的网格无关性检验,如表2所示。

表2 网格无关性检验
表中为单周期液膜网格单元数量;1和2分别为两模型的单周期液膜开启力;1和2分别为前后两次开启力的相对误差。随着网格数量的增加,两模型的开启力趋于稳定,当相对误差小于0.5%时,认为网格数量的变化对计算结果的影响可以忽略,因此综合考虑数值计算精度和时间成本,选用网格数为479037的模型进行计算。
李京浩[17]采用开放式的密封结构,同时利用透明材料制作其中一密封环,实验观察斜直线槽密封间隙中的水介质流动状态,观测出如图6(a)所示的空化区域(图中白色发亮部分)。图6(b)为采用文献[17]的参数,利用建立的空化热效应模型对斜直线槽机械密封进行计算的结果。实验观测和数值计算结果表明,空化位置和形状特征基本一致。

图6 空化热效应模型适用性验证
2 计算结果及讨论
2.1 空化热效应对开启力的影响
为便于开启力的对比分析,定义相对开启力增量为
式中,r为模型1的开启力,ra为模型2的开启力。
图7为两种模型的液膜开启力随转速变化曲线图。由图7(a)可见,转速由小增大过程中,液膜开启力并没有持续上升,而是存在极大值,对于本文研究对象及工况而言,极大值出现在转速约为5000 r·min-1处。这一变化规律主要与液体黏温特性有关,低转速时,液膜内摩擦热量较小,黏度变化较小,流体的动压效应和泵送效应随转速的增强而增强,开启力呈上升状态;转速超过5000 r·min-1之后,液膜内摩擦热量增大,温度升高,且随着转速的升高而明显升高,黏度随之下降,削弱了动压效应和泵送效应,开启力随转速逐步降低。由图7(a)、(b)还可以看出,低转速时,空化热效应并不明显,在常规的5000 r·min-1以下,空化热效应与开启力几乎无关;转速高于5000 r·min-1后,受空化热效应的影响,开启力呈现降低现象,且随着转速的增大开启力的下降量增大,即值增大。这说明低转速时,液膜空化程度低甚至未发生空化,随转速的提升空化不断加剧,空化热效应导致的开启力负增量越来越明显。

图7 两模型的开启力对比
为了深入分析产生上述现象的原因及空化热效应对密封润滑性能的影响机理,本文将选取3000 r·min-1和13000 r·min-1两个转速对两种模型的压力场、温度场、泵送量及空化区域进行对比分析。
2.2 空化热效应对压力分布的影响
图8为两种模型分别在转速为3000 r·min-1和13000 r·min-1下的液膜厚度方向不同位置(-1.5 μm,0 μm,1.5 μm,3 μm,下同)的压力分布云图。两模型的高压区域均出现在槽根附近,且液膜轴方向压力分布规律基本一致。由图8(a)、(b)可知,在转速为3000 r·min-1时,最大压力max分别为4.78 MPa和4.77 MPa,大小基本相等,且两者高压区域的大小和变化梯度也基本一致;而在转速为13000 r·min-1时,由图8 (c)、(d)可知,模型2的最大压力值max4.73 MPa,而模型1的最大压力值为max5.12 MPa,模型2槽根高压区最大压力值和变化梯度明显比模型1小,导致模型2的液膜开启力为707.8 N,而模型1的液膜开启力为811.7 N,如图7(a)所示。

图8 转速为分别为3000 r·min-1和13000 r·min-1时两模型压力分布云图
而在低压区域,由图8可知,模型1在槽的周向扩散侧出现了明显的局部低压区,而模型2没有这一现象。由图8(a)、(c)可知,模型1的低压区域增加明显,这是由于在高转速时,液膜流体周向速度加快,螺旋槽台阶扩散段相应的压力下降区域增大。为了更好地显示和分析低压区的压力分布情况,将转速13000 r·min-1时两模型的低压区压力分布进行细化,如图9所示。由图可知,两图的低压区域大小基本一致,但模型1由于没有考虑空化热效应的影响,饱和汽化压力为温度293 K时的饱和汽化压力2.3 kPa(绝对压力)。而模型2低压区域压力明显比模型1的高,而且低压区域压力也不再是一定值。这是由于密封转动生成黏性摩擦热导致液膜温度升高,产生空化热效应,水的饱和汽化压力随温度的升高而明显升高,即出现空化时相应的空泡内压力也升高。由于两者都考虑了空化的作用,因此饱和汽化压力表征了液膜间隙各处温度能出现的最小压力值,从而出现了两模型低压区域分布不同的情况。

图9 转速为13000 r·min-1时两模型低压区压力分布云图
由上述分析可知,由于膜厚很小,压力分布在膜厚方向基本没有变化。虽然两模型的低压区压力分布不同,模型2因考虑空化热效应低压区压力增大,但最大的压力仅为34 kPa,对开启力的贡献很有限,主要还是槽根处高压区的压力分布决定液膜开启力的大小。在高转速情况下,由于空化热效应,导致模型2的高压区形成能力减弱,从而使液膜的开启力明显减小。
2.3 空化热效应对泵送量的影响
由图10可知,在低转速时,两模型的泵送量都随着转速的增加呈先上升后逐渐趋于平缓直至下降的规律,这是因为随着转速的增加,液膜温度升高,黏度降低,到达一定转速后剪切力开始减小,泵送量减小。
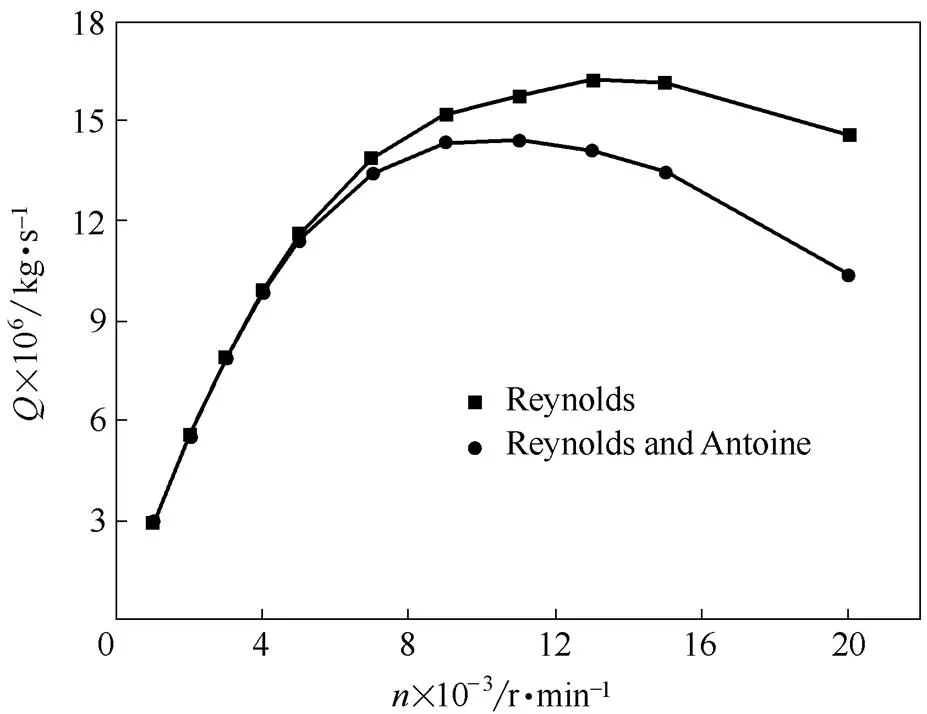
图10 两模型在不同转速下的泵送量
当转速在10005000 r·min-1之间时,两模型的泵送量基本相等;而当转速继续增加时,考虑空化热效应的模型2的泵送量小于模型1,且随转速的增大其差值越来越大;通过泵送量变化规律与开启力的变化趋势[图7(a)]的比较表明,当转速高于5000 r·min-1后,虽然泵送量在增大,但动压效应因温度的升高和黏度的下降而减弱,开启力呈下降趋势;同时说明空化的热效应在高转速时使泵送效应减弱。
2.4 空化热效应对液膜温度的影响
由图 11可知,两模型的动环端面平均温度都随转速的增加而增加,这是间隙液膜黏性耗散热增加所致。
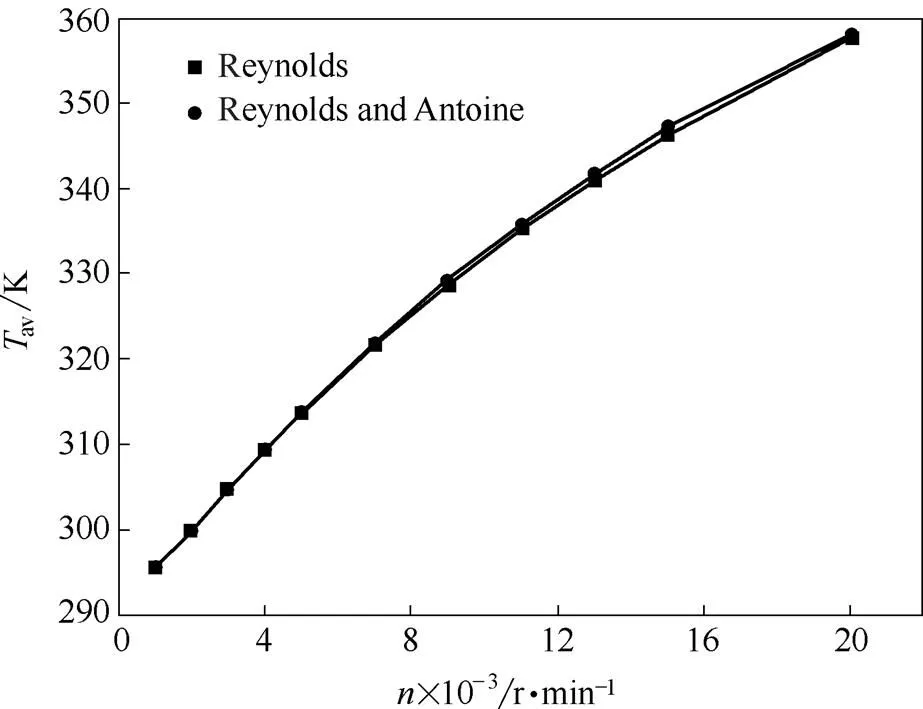
图11 两模型的动环端面平均温度
图12为两模型液膜厚度方向不同位置温度分布云图。由图可知,螺旋槽区域及附近温度低于外径处的温度,这是因为一方面螺旋槽区域液膜厚度较大且内径处线速度较小,导致速度梯度减小,黏性耗散热减小;另一方面,螺旋槽的泵送作用使对流传热增强,导致液膜温度较低且趋向平均,这与文献[18]的分析一致。两模型各个剖面的温度分布基本一致,模型2仅在螺旋槽槽区局部温度比模型1稍高。
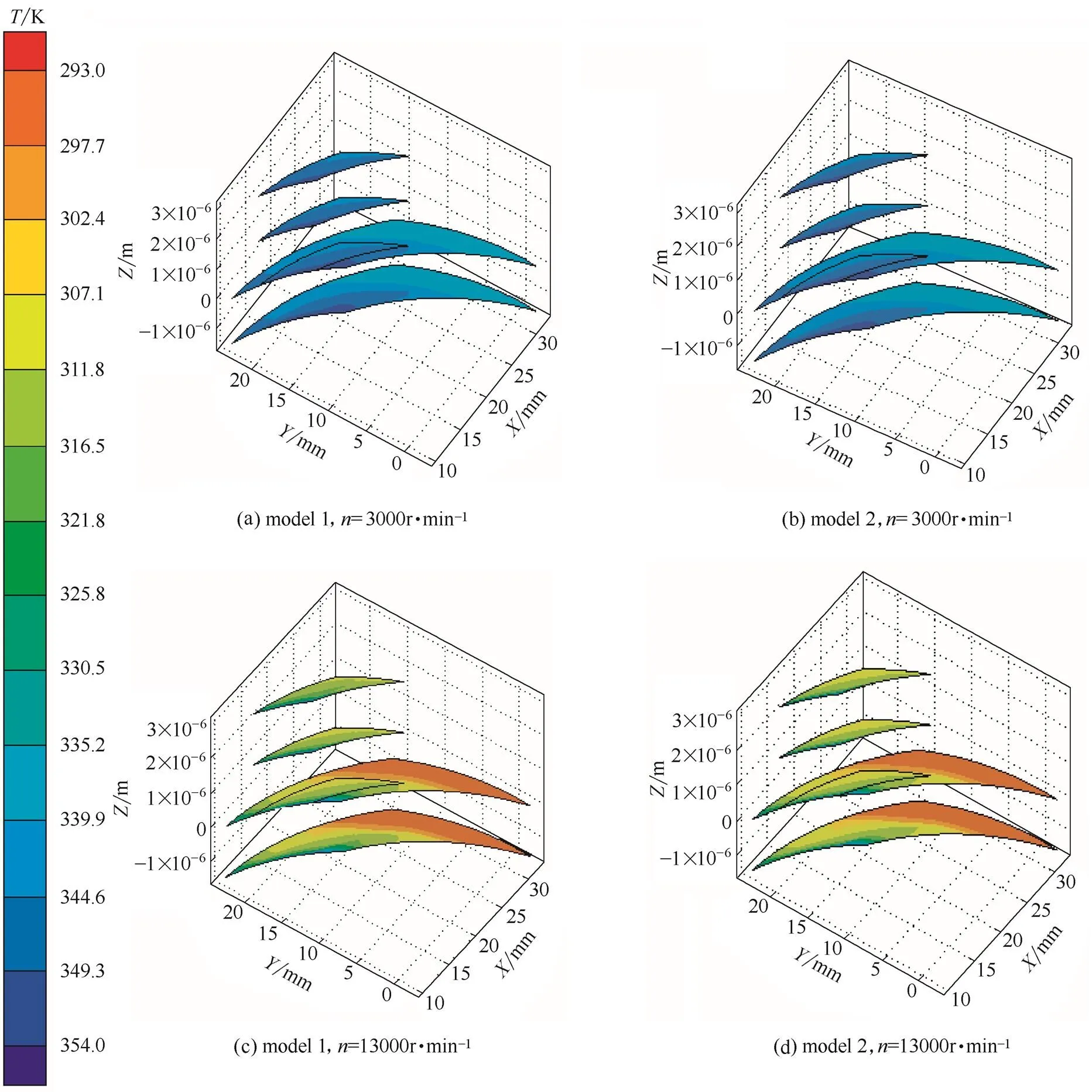
图12 转速为3000、13000 r·min-1时两模型的温度分布云图
2.5 空化热效应对空化区域的影响
由图 13可知,两种模型动环端面的空化泡平均体积分数均随着转速的增加而增加,说明空化热效应并没有改变因液膜流速增大而导致台阶扩散通道压力下降和空化产生的规律。同时,图13还表明,动环端面的空化程度与空化热效应有关,随着转速的增大,考虑空化热效应时的动环端面空化程度增幅更大。

图13 动环端面平均气泡体积分数
图14为转速为3000 r·min-1和13000 r·min-1时液膜厚度方向不同位置的空化区域分布云图。由图可知,两模型的液膜空化区域均发生在槽台阶扩散低压区,且随着转速的增大空化区域增大。但两模型的空化程度及分布规律不同,模型1的空化程度沿轴向槽底方向逐渐加剧,而模型2正好相反,也就是模型1的槽底为空化程度最高部位,而模型2的动环表面槽区位置为空化程度最高位置,槽底空化程度非常低。由于空化导致气泡增加,混合黏度和能量耗散降低,因此,上述两模型空化区域的不同导致模型2仅在螺旋槽凹槽处温度比模型1稍高一些。由前面综合分析已知,图9处模型2低压区压力在膜厚方向上基本没有变化,但低压区的温度在槽深方向上是逐渐降低的,根据饱和汽化压力和温度的对应关系,温度降低,饱和汽化压力降低,但槽底附近的压力大小及分布和动环面上基本相等,导致压力并没有降低到对应温度的饱和汽化压力,从而使空化区域减小。这些现象说明空化热效应对空化程度及分布有显著的影响,其影响结果与温度分布、压力分布等因素密切相关。
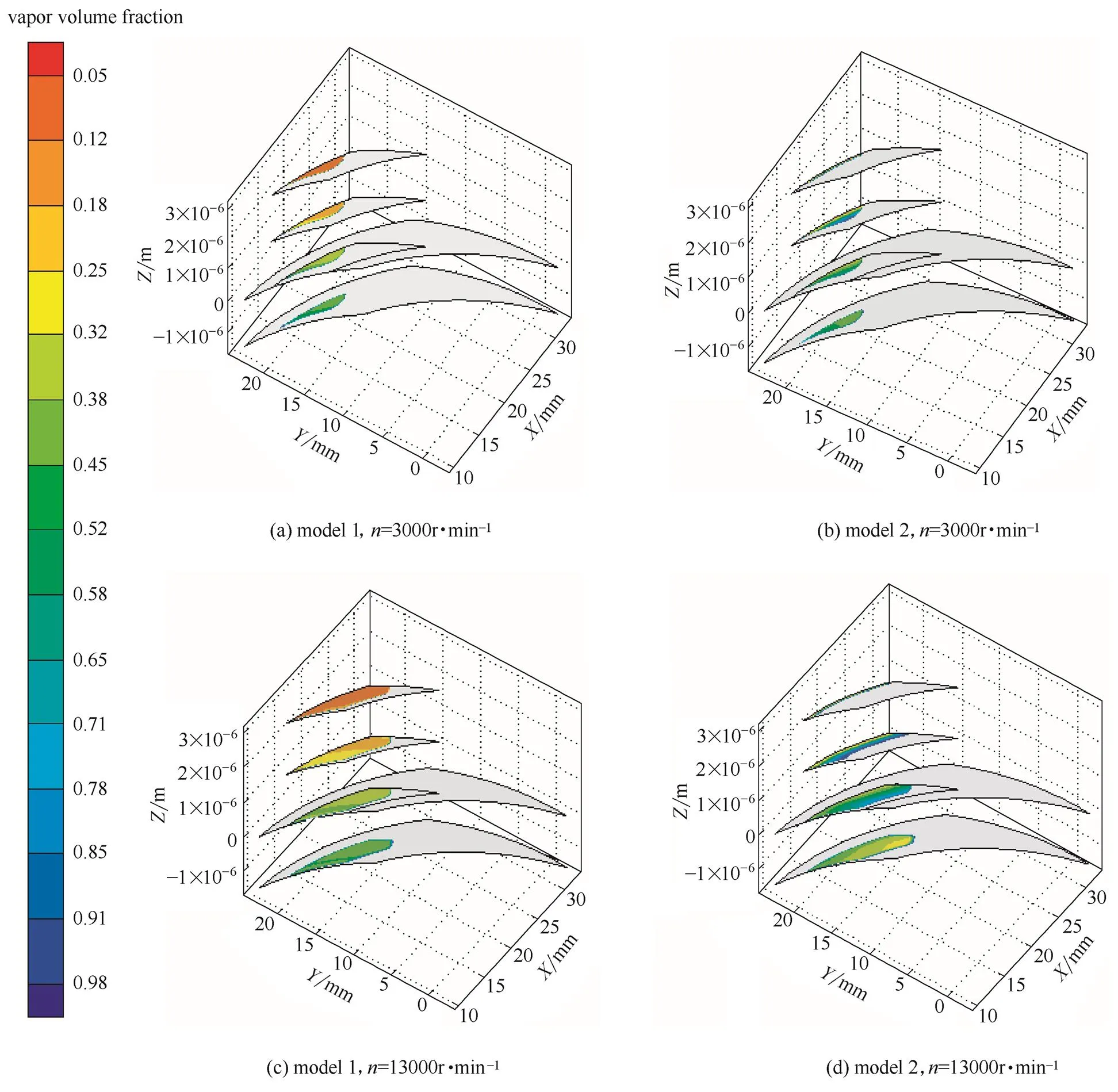
图 14 转速为3000和13000 r·min-1时两模型的空化区域分布云图
3 结 论
(1)在低转速下,空化热效应对密封性能的影响可以忽略,但在高转速下空化热效应使上游泵送机械密封的高压区形成能力减弱,泵送量降低,开启力降低。在高转速工作条件下分析密封失效机理时,除了考虑黏温效应之外,还要考虑空化热效应的影响。
(2)空化热效应对密封端面间液膜温度分布的影响小,相比于仅考虑黏温效应的模型,螺旋槽槽区局部温度稍有提升。
(3)与仅考虑黏温效应的模型相比,考虑空化热效应后,得到的空化分布和程度明显不同。仅考虑黏温特性时,在液膜厚度方向空化区域大小基本相等,但静环槽底的气泡体积分数最大,空化程度最严重。而综合考虑黏温特性和空化热效应时,动环端面空化程度最严重,由动环端面沿膜厚方向至静环槽底,空化区域越来越小,槽底空化区域最小。
符 号 说 明

cp ——水的比热容,J·kg-1·K-1 Fcond——冷凝系数 Fr——模型1的开启力,N Fra——模型2的开启力,N Fvap——蒸发系数 F1,F2——分别为模型1、模型2的单周期液膜开启力,N G——相对开启力增量,% N——单周期液膜网格数 n——相数 Re,Rc——分别为气泡产生、溃灭源项 rB——气泡半径,mm T——水温,℃ v——空泡相 vm——质量平均速度,m·s-1 α——气相体积分数 αnuc——气核体积分数 β——黏温系数,取0.03℃-1 δ1,δ2——分别为模型1、模型2前后两次的开启力相对误差,% η——温度T时的黏度,kg·m-1·s-1 η0——温度T0时的黏度,kg·m-1·s-1 λ——水的热导率 μm——混合黏性系数 ρm——混合物密度,kg·m-3
References
[1] FINDLEY J A. Cavitation in mechanical face seals [J]. Journal of Lubrication Technology, 1968, 90 (2): 356-364.
[2] JAKOBSSON B, FLOBERG L. The finite journal bearing, considering vaporization [J]. Transactions of Chalmers University of Technology, 1957, 190: 1-116.
[3] OLSSON K O. Cavitation in dynamically loaded bearings [J]. Transaction of Chalmers University of Technology, 1965, 308: 1-60.
[4] ELROD H G. A cavitation algorithm [J]. Journal of Lubrication Technology,1981, 103 (3): 350-354.
[5] LEBECK A O. Experiments and modeling of zero leakage backward pumping mechanical face seals [J].Tribology Transactions,2008, 51 (4): 389-395.
[6] DJAMAÏ A, BRUNETIÈRE N, Tournerie B. Numerical modeling of thermohydrodynamic mechanical face seals [J]. Tribology Transactions, 2010, 53 (3): 414-425.
[7] QIU Y, KHONSARI M M. Performance analysis of full-film textured surfaces with consideration of roughness effects [J]. Journal of Tribology, 2011, 133 (2): 021704(1-10).
[8] MENG X K, BAI S X, PENG X D. Lubrication film flow control by oriented dimples for liquid lubricated mechanical seals [J]. Tribology International, 2014, 77: 132-141.
[9] 唐飞翔, 孟祥铠, 李纪云, 等. 基于质量守恒的LaserFace液体润滑机械密封数值分析 [J]. 化工学报, 2013, 64 (10): 3694-3700. TANG F X, MENG X K, LI J Y,. Numerical analysis of LaserFace liquid mechanical seal based on mass conservation [J]. CIESC Journal, 2013, 64 (10): 3694-3700.
[10] PASCOVICI M D, ETSION I. A thermo-hydrodynamic analysis of a mechanical face seal [J]. Journal of Tribology, 1992, 114: 639-645.
[11] LEBECK A O. Principles and Design of Mechanical Face Seals [M]. New York: Wiley-Interscience Publication, 1991.
[12] BRUNETIÈRE N, MODOLO B. Heat transfer in a mechanical face seal [J]. International Journal of Thermal Sciences, 2009, 48 (4): 781-794.
[13] 中国科学院. 科学数据库——工程化学数据库[DB/OL]. http://www.sdb.ac.cn,2004. Chinese Academy of Sciences. Scientific Database—Chemical Engineering Database [DB/OL]. http://www.sdb.ac.cn, 2004.
[14] BRENNEN C E. Cavitation and Bubble Dynamics [M]. Oxford: Oxford University Press, 1995.
[15] 温诗铸, 黄平. 摩擦学原理[M]. 4版. 北京: 清华大学出版社, 2012: 9. WEN S Z, HUANG P. Principles of Tribology [M]. 4th ed. Beijing: Tsinghua University Press, 2012: 9.
[16] CHEN H L, XU C, ZUO M Z,. The thermal and mechanical deformation study of up-stream pumping mechanical seal [J]. IOP Conference Series: Materials Science and Engineering, 2015, 72: 042032.
[17] 李京浩. 机械密封空化效应的数值计算方法与实验研究[D]. 北京: 清华大学, 2011. LI J H. Numerical computing method and experimental study for cavitation in mechanical seals [D]. Beijing: Tsinghua University, 2011.
[18] QIU Y, KHONSARI M M. Thermohydrodynamic analysis of spiral groove mechanical face seal for liquid applications [J]. Journal of Tribology, 2012, 134 (2): 021703 (1-11).
Influence of cavitation thermal effect on lubrication properties of upstream pumping mechanical seal
CHEN Huilong, WANG Bin, REN Kunteng, LI Tong, ZHAO Binjuan
(School of Energy and Power Engineering, Jiangsu University, Zhenjiang 212013, Jiangsu, China)
Cavitation occurred at mechanical seal faces is an important factor affecting lubrication properties of the mechanical seal. A computational fluid dynamics model was established from Antoine equation with a consideration of cavitation thermal effect. The cavitation thermal effect on the sealing performance was analyzed and compared to results of commonly used model of viscosity-temperature effect of liquid film on seal faces. The results indicated that the influence of cavitation thermal effect was negligible at low rotating speed whereas weakened the capacity of forming high-pressure region in mechanical seal at high rotating speed, which reduced pumping rate and opening force. Both viscosity-temperature effect and cavitation thermal effect were needed to analyze seal failure mechanism at high rotating speed. The local temperature at the spiral groove was slightly higher from cavitation thermal effect than that from viscosity-temperature effect. With the cavitation thermal effect, degree of cavitation occurred most seriously in the rotating ring face and cavitation space became smaller with the smallest one in groove bottom from the rotating ring face to the stationary ring groove bottom, which was contrary to those by considering viscosity-temperature effect.
mechanical seal; hydrodynamic lubrication; cavitation; thermodynamic properties; computational fluid dynamics; model; stability
2016-04-08.
Prof.CHEN Huilong, huji@ujs.edu.cn
10.11949/j.issn.0438-1157.20160456
TH 117.2
A
0438—1157(2016)10—4334—10
国家自然科学基金项目(51279067)。
2016-04-08收到初稿,2016-07-12收到修改稿。
联系人及第一作者:陈汇龙(1961—),男,博士,教授。
supported by the National Natural Science Foundation of China (51279067).

